基于改进行程时间估计模型的最优路径选择

陈诗意 潘义勇 魏双秋

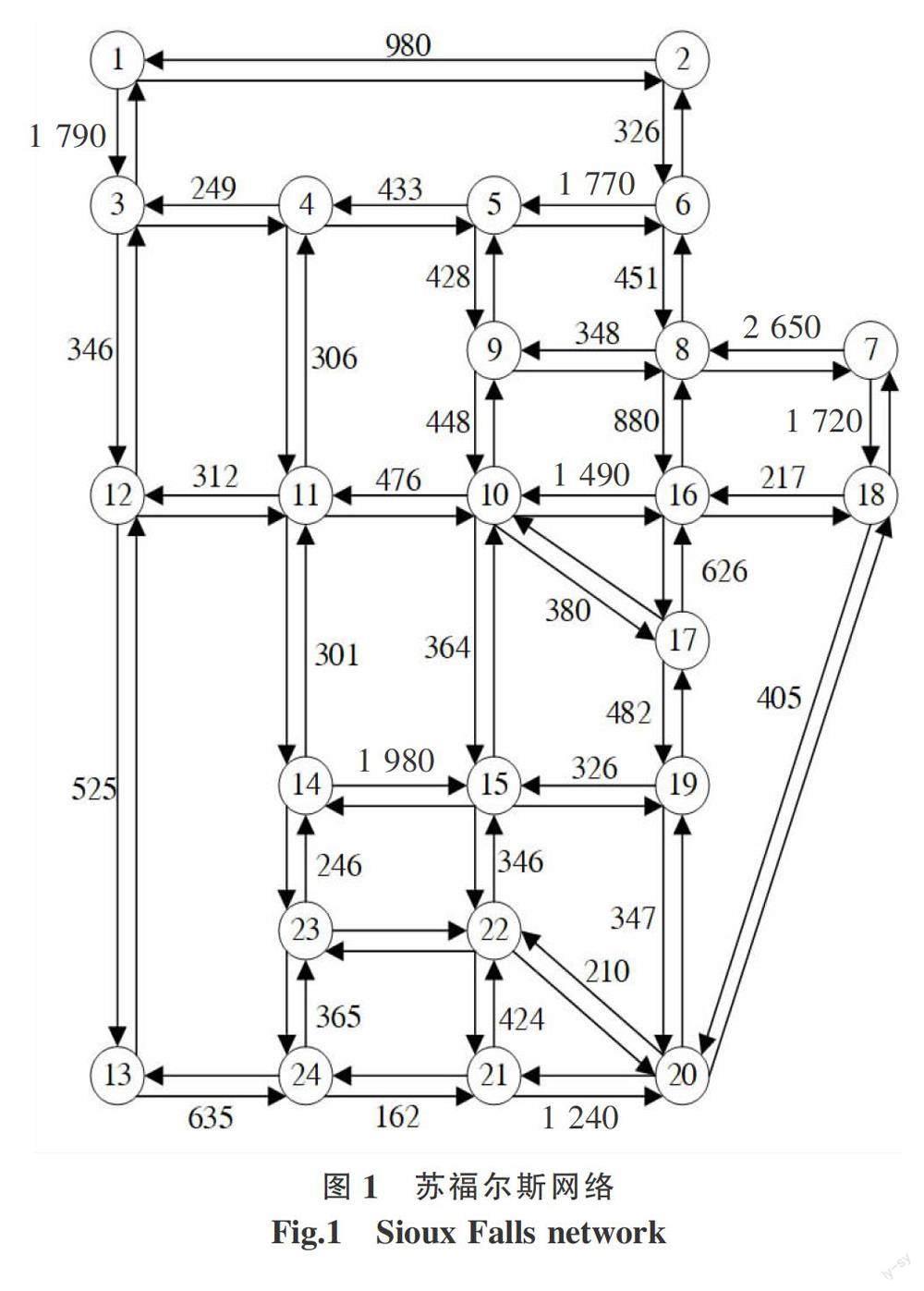
摘要：为解决交通网络最优路径问题，提出改进的行程时间估计模型，并设计基于该模型的最优路径算法。行程时间估计模型在分段截断二次速度轨迹模型的基础上进行改进，用路段节点的到达速度代替同一出发时刻下测得的速度，通过构造在时间和空间上连续的速度轨迹来估计行程时间。首先，基于Yen′s KSP算法以路段距离为阻抗求解K条最短路径;其次，分别用改进的行程时间估计模型估计K条最短路径的行程时间;最后，以行程时间为成本选择最优的路径。通过Sioux Falls网络的数值试验验证模型和算法的有效性和优越性。试验結果表明：改进的分段截断二次速度轨迹模型相比于原始模型精度平均提高了65%;算法的最优路径结果能减少路径经过的交叉口数和缩短最优路径的总长度，而且最优路径的行程时间估计结果与真实值的MAPE保持在3%内。

关键词：智能交通;行程时间;最优路径选择;KSP

中图分类号：U491.1+3 文献标志码：A

本文引用格式：陈诗意，潘义勇，魏双秋. 基于改进行程时间估计模型的最优路径选择[J]. 华东交通大学学报，2023，40（1）：60-66.

Optimal Path Selection Based on Improved Travel Time

Estimation Model

Chen Shiyi， Pan Yiyong， Wei Shuangqiu

（College of Automobile and Traffic Engineering， Nanjing Forestry University， Nanjing 210037， China）

Abstract：To solve the optimal path problem of the traffic network， an improved travel time estimation model was proposed， and an optimal path algorithm based on this model was designed. The travel time estimation model was improved on the basis of the segment truncated quadratic velocity trajectory model by replacing the velocity measured at the same departure moment with the arrival velocity of the road segment nodes， and the travel time was estimated by constructing a velocity trajectory that is continuous in time and space. The optimal path algorithm based on travel time estimation firstly solved K shortest paths based on Yen′s KSP algorithm with road section distance as impedance， then estimated the travel time of K shortest paths by the improved travel time estimation model respectively， and finally selected the optimal path with travel time as cost. The validity and superiority of the model and algorithm were verified by numerical experiments of Sioux falls network. The experimental results show that the improved segmented truncated quadratic speed trajectory model improves the accuracy by an average of 65% compared with the original model and the optimal path results based on the proposed algorithm can reduce the number of intersections the path passes through and shorten the total length of the optimal path. Moreover， the estimated results of the optimal path's travel time stay within 3% of the real value of MAPE. The results of this study may provide a theoretical basis for the optimal path method for traffic networks.

Key words： intelligent transportation; travel time; optimal path selection; KSP

Citation format：CHEN S Y，PAN Y Y，WEI S Q. Optimal path selection based on improved travel time estimation model[J]. Journal of East China Jiaotong University，2023，40（1）：60-66.

最优路径问题是ITS系统子系统路径诱导系统的核心，而可靠的行程时间估计是进行路径诱导的前提[1-2]。现有的路径诱导系统一般基于当前或历史数据提供路线方案，但由于缺少考虑交通信息的变化，导致决策的路径无法有效避免拥堵[3-4]。基于交通网络动态信息估计行程时间优化路径诱导算法，对提高出行效率具有重要意义。

现状的交通网络最优路径算法主要分为两类：一类是基于Dijkstra算法的启发式算法，另一类是基于行程信息的K最优路径算法。Wen等[5]提出了两种基于传统Dijkstra的启发式算法：启发式算法一可以將Dijkstra算法求得的初始路径解保存在中间节点的标签中;启发式算法二和Huang等[6]提出的类似，使用时空扩展网络，将时间区间分成离散的几个时间间隔，只有每个时间间隔的最小成本标签被保存在中间节点。在实际应用中，路径诱导系统需根据路阻随时间的变化来计算路径，故基于当前静态的交通信息计算的最优路径不能保证它是全局最优的[7-8]。K最优路径（K shortest paths， KSP）算法可以提供K条路径方案，弥补了静态最优路径算法的缺陷，有部分学者采用K最优路径算法求解网络最优路径问题。Fu等[9]提出基于Shier的K最短路径算法的启发式算法，通过检查参数K可以找到潜在最优路径而不需要枚举所有路径。段宗涛等[10]应用了KSP算法获得K条最优路径，通过对路径集合按设计通行能力划分等级，将交通流按权重分配到不同等级的K条路径上，提高整个交通网络的资源利用率。Hu等[11]提出了一种平衡重叠和行程时间偏差的K最短路径算法，该算法包含实时更新信息的网络模型，并通过惩罚函数和行程时间约束K条路径，该算法可以有效筛选大量的K条最优路径的结果。综上所述，启发式最优路径算法计算时间长，难以运用于大型网络中，而KSP算法鲁棒性强，时间复杂度低。有必要结合KSP算法和行程时间估计模型来优化交通网络最优路径算法，以获得有效的最优路径。

1 行程时间估计

行程时间一般可以通过区间检测器直接获得，但此方法容易累积设备的计数误差，故目前研究中常将行程时间作为变量，通过其他交通相关变量构造模型来估计行程时间[12]。而在众多的交通变量中，速度相较于其他反映交通流特征的变量如交通流、密度更容易获得。研究选择构建基于速度的行程时间估计模型。

经典分段截断二次速度轨迹模型[13]利用相邻的3个路段节点速度构造连续的、平滑的速度轨迹，如式（1）所示。该模型用各节点在同一出发时刻t的速度构造速度轨迹，故存在速度轨迹在时间维度不连续的问题，只适用于距离足够短的路径或交通运行状态良好的高速公路。针对该问题，提出了改进的分段截断二次速度轨迹模型，模型考虑了行程中交通状态变化对速度的影响，利用到达节点的速度v[ATm（t），xm]代替出发时刻速度v（t，xm），改进模型如式（2）所示。改进的模型不受限于通过路段的时间间隔足够小，或要求路段的交通流是稳定流的条件，符合实际交通网络的应用。

v（τ）≈v（t，x2m-1）l2m-1（τ）+v（t，x2m）l2m（τ）+v（t，x2m+1）l2m+1（τ）

（1）

v（τ）≈v[AT2m-1（t），x2m-1]l2m-1（τ）+v[AT2m（t），x2m]l2m（τ）+

v[AT2m+1（t），x2m+1]l2m+1（τ）（2）

式中：t为出发的时刻;v（τ）为相邻2个路段的速度轨迹;v[AT2m-1（t），x2m-1]，v[AT2m（t），x2m]和v[AT2m+1（t），x2m+1]分别为到达第2m- 1个，第2m个和第2m+1个这3个相邻路段节点处的速度;插值点τ∈[AT2m-1（t），AT2m+1（t）];x2m-1、x2m和x2m+1第2m-1个、第2m个和第2m+1个这3个相邻路段节点的位置;l2m-1（τ），l2m（τ）和l2m+1（τ）均为拉格朗日二次基函数。基函数为

l2m-1（τ）=

l2m（τ）=

l2m+1（τ）=

（3）

考虑到车辆在道路上的加减速行为，引入了常基函数作为边界速度限制，用历史数据的85%最大最小值构造常基函数vmax和vmin，当超过该值时就被边界速度代替。当τ∈[AT2m-1（t），AT2m+1（t）]，通过相邻3个路段节点时刻的速度与边界速度值的关系为

v[AT2m-1（t），x2m-1]l2m-1（τ）+v[AT2m（t），x2m]l2m（τ）+

v[AT2m+1（t），x2m+1]l2m+1（τ）-vmax=0（4）

v[AT2m-1（t），x2m-1]l2m-1（τ）+v[AT2m（t），x2m]l2m（τ）+

v[AT2m+1（t），x2m+1]l2m+1（τ）-vmim=0（5）

式中：τ为取到最大速度vmax或最小速度值vmin的时刻。

根据上述改进的分段截断二次速度轨迹模型可以构造时刻出发的车辆速度轨迹。假设OD节点之间共有M个节点，路段行程时间和OD点的行程时间可分别由式（6）和式（7）计算

TT（t;xm，xm+1）=ATm+1（t）-ATm（t）=（6）

TT（t;O，D）=ATM（t）-AT1（t）=TT（t，xm，xm+1）=

（7）

式中：TT（t;xm，xm+1）为路段的行程时间;TT（t;O，D）为OD节点间的行程时间;ATm（t）为到达第m个节点处的速度;v[τm（t）]为区间[ATm（t），ATm+1（t）]的平均速度。

2 交通网络最优路径问题

2.1 基于距离阻抗的交通网络模型

在估计各路径行程时间前，需求解起讫点之间所有可能的路径，根据主要交叉口和道路之间的连接情况，建立基于路段距离的交通网络模型。对于网络图G（V，A，L），V={V1，V2，…，VN}是交通网络节点的集合;A是弧的集合，A?V×V，表示交通网络中的路段;L是边的集合，lij（lij∈L）表示边Ak=（ViVj）的权值，是非负的实数，代表节点Vi和节点Vj之间的阻抗，如果lij=∞则表示节点Vi和Vj之间无边相连。

在传统的最优路径问题中，通常假设网络边的权值不变，不能真实反映实际的交通网络。为了描述交通网络路段权值的变化，需结合行程时间估计模型估计路径的耗时。

2.2 问题描述

在实际出行中，出行者往往遵循“路径行程时间最小化”目标选择路径，故本研究的最优路径以行程时间作为费用考虑。由于行程时间因不同的出发时刻而异，而且与路段的交通状态有关，如果使用原始的分段截断二次速度轨迹模型估计行程时间，即根据出发时刻下测得的各节点速度来构造速度轨迹，相当于在当前的交通状态下估计行程时间，故基于该行程时间的最优路径相当于静态的路径[14-16]。改进的行程时间估计模型由于考虑了速度在行程中的变化，构造的速度在时间和空间上连续，故行程时间能接近真实值。当获得起讫点间所有可能的路径，再用改进的行程时间估计模型估计路径的行程时间，以时间成本最少为选择策略，就可以得到最优路径。综上所述，基于行程时间估计的最优路径算法不需要考虑整个交通网络所有的路段ViVj（ViVj∈A）的行程时间，只需确定路径和路径经过的节点。

Yen′s KSP算法是典型的偏离路径算法，适用于求解限定无环的K最优路径，与实际出行的要求相符。Yen′s KSP算法核心思想是循环使用Dijkstra：每次把前一条最短路径Pk（k

对于K最短路径集合中的路径Pk（k=1，2，3，…，K），可以根据式（2）～式（5）用该路径的节点到达速度来构造改进分段截断二次速度轨迹，根据式（7）求解路径起讫点之间的行程时间TT（t;O，D）。

以路径行程时间为费用，行程时间最小的路径即最优路径，则t时刻从原点出发到达终点的最优路径Pk为

Pk=arg min{TT（t;O，D）}=arg min{TT（t;xm，xm+1）}

（8）

式中：Pk为行程时间费用最小的路径，k=1，2，3，…，K，K为最短路径数;TT（t;xm，xm+1）为路径Pk的行程时间。

3 算法求解及算法复杂性分析

3.1 算法设计

为求解交通网络最优路径，设计基于Yen′s KSP算法和改进行程时间估计模型的最优路径算法。首先以路段距离作为权重，将试验网络的路权以矩阵形式存储，将OD点和网络权重矩阵输入Yen′s KSP算法，输出K条最短路径集合，而且集合内的路径按距离长度由小到大排序。将输出的前K条距离最短的路径分别用改进的分段截断二次速度轨迹模型估计行程时间，确定出发时刻和K条最短路径的各个节点的到达速度，用到达速度代替出发时刻速度，构造在时间和空间域连续的速度轨迹，最后以时间成本为决策，选择耗时最短的路径作为最优路径。具体算法步骤如下。

第1步 用Yen′s KSP算法计算K条距离最短路径。确定试验网络，以路段距离为权重存储网络的权重矩阵，用Yen′s KSP算法搜索原点O到终点D的K条距离最短的初始路径，输出前K条距离最短的路径集合。

第2步 用节点的到达速度构造在时空域连续的速度轨迹。确定出发时刻t，分别确定第1步输出的前K条距离最短的路径Pk（k=1，2，3，…，K）各个节点的到达时刻速度，用到达节点时刻的速度v[ATm（t），xm]输入改进的分段截断二次速度轨迹模型，由拉格朗日二次插值基函数和常基函数构造在时间上连续的速度轨迹v（τ）。

第3步 分别估计K条最短路径的行程时间。对这K条路径Pk（k=1，2，3，…，K）分别求速度轨迹v（τ）在子路段的平均速度v[τm（t）]，m=1，2，3，…，M-1，最后根据式（7）估计路径的行程时间TT（t;O，D）。

第4步 对K条路径的行程时间成本按从小到大排序。

第5步 将行程时间耗时最少的路径作为最优路径。以路径行程时间为费用，行程时间最小的路径Pk即最优路径。

3.2 算法复杂性分析

在不考虑数据结构的前提下，算法复杂性表现为时间复杂度。Dijkstra算法计算两点间的最优路径时间复杂度为O（m+nlogn）;每条候选路径Pk+1最多包含n个节点，求解每个节点到目的节点偏离路径时间的复杂度是O（n×（m+nlogn））;假设结果列表中最多有K条无环路径，把新的偏离路径放入候选路径集中的算法复杂度是O（logK）;从候选路径集pk+1中最多有n条路径，从中选择最短的路径时间复杂度是O（n）;用改进的分段截断二次函数估计行程时间的算法复雜度是O（（i×j）+2i），其中，i是插值数，j是节点数[17-18]。综上，基于行程时间估计的最优路径算法的复杂度为O（K（nm+n2logn）+logK+n+i（j+2））。

4 对比试验

4.1 试验网络

为了检验基于行程时间估计最优路径算法的可行性，针对Sioux Falls（SF）网络开展数值试验。Sioux Falls（SF）网络拓扑结构图如图1所示，该网络由24个节点和76条路段组成，图中各路段权值代表路段的长度，路段双向的权值相等。其中，道路网络各个节点在不同时间间隔内的速度如表1所示，t是从原点出发的时刻，Δt是获取速度数据的间隔，Δt取5 min。

4.2 K最短路径集

用Yen′s KSP算法按路径长度搜索节点的前5条最短路径，起讫点为1→24，3→20和7→13情景下的前5条最短路径按长度增序排列，结果如表2所示。

4.3 试验结果的对比与分析

4.3.1 行程时间估计误差分析

在3种不同起讫点情景下，以最短路径P1为例，分别用改进的分段截断二次速度轨迹模型和原始模型估计最短路径的行程时间，结果如图2所示。改进的分段截断二次速度轨迹模型估计路径的行程时间更接近真实值，而原始模型估计的行程时间容易出现高估的情况。进一步计算两种模型的平均绝对百分比误差（MAPE），得到量化模型的拟合效果，如表3所示。改进的行程时间估计模型拟合度较高，MAPE值均保持在5%以内，有效地提高了原始模型的精度，精度平均提高65%。

4.3.2 最优路径结果分析

将基于改进行程时间估计模型和基于原始模型的最优路径结果进行对比和分析，最优路径结果如表3中所示。为了评价上述两种算法的性能，分别设置3种起讫点（1→24，3→20和7→13）情景，以路径耗时、路径长度和与真实时间的MAPE作为评价指标。数值试验结果显示两种算法下计算的行程时间最优路径不完全相同，由试验结果分析可以得到以下结论。

1） 从路径经过的节点数看，当起讫点为1→24时，两种算法计算的最优路径不相同，基于改进模型的最优路径比基于原始模型的最优路径经过的节点数减少30%。

2） 从行程时间耗时看，通过考虑路况速度的变化，用到达节点的速度代替出发时刻下的同一速度构造速度轨迹，估计的行程时间更符合实际。当起讫点为3→20和7→13时，尽管两种算法的最优路径结果相同，但行程时间不同：基于改进行程时间估计的最优路径比基于原始模型的最优路径更接近真实时间，MAPE值分别为0.25%和2.96%。

3） 从行程的轨迹看，以上3种起讫点下基于改进行程时间估计模型的最优路径结果与距离最短路径结果相同。而且起讫点为1→24时，虽然基于行程时间估计的最优路径耗时仅比基于原始模型的最优路径多1.7%，但路径总长比基于原始模型的最优路径缩短3.1%。

综上所述，基于行程时间估计的最优路径算法更具有实际意义且更有效。

5 结论

1） 改进的行程时间估计模型拟合度平均比原始模型提高了65%。

2） 基于本文模型估计的最优路径时间成本不总是少于原始模型，但更接近真实值，与真实值的MAPE均保持在3%以内。

3） 基于本文算法的最优路径结果能减少路径经过的交叉口数和缩短最优路径的总长度，路径总长比基于原始模型的最优路径缩短3.1%。

参考文献：

[1] 闫茂德，常楠楠，张昌利. 城市快速路网行程时间计算与最优路径选择算法[J]. 西南交通大学学报，2014，49（5）：811-816.

YAN M D，CHANG N N，ZHANG C L. Travel time computation and optimal path selection algorithm of urban expressway network[J]. Journal of Southwest Jiaotong University，2014，49（5）：811-816.

[2] 智路平，周溪召. 基于动态行程时间可靠性的单车辆路径选择算法研究[J]. 公路交通科技，2018，35（9）：8.

ZHI L P，ZHOU X Z. Study on single vehicle routing algorithm based on dynamic travel time reliability[J]. Journal of Highway and Transportation Research and Development，2018，35（9）：8.

[3] KIM J，HAN W S，OH J，et al. Processing time-dependent shortest path queries without pre-computed speed information on road networks[J]. Information Sciences，2014，255： 135-154.

[4] 姚丽亚，关宏志，魏连雨，等. 基于实时交通信息的行程时间估算及路径选择分析[J]. 公路交通科技，2006（11）：86-89.

YAO L Y，GUAN H Z，WEI L Y，et al. Study on link travel time estimation and route selection method based on real-time traffic information[J]. Journal of Highway and Transportation Research and Development，2006（11）：86-89.

[5] WEN L，CATAY B，EGLESE R，et al. Finding a minimum cost path between a pair of nodes in a time-varying road network with a congestion charge[J]. European Journal of Operational Research，2014，236（3）：915-923.

[6] HUANG Y，ZHAO L，VAN W，et al. Time-dependent vehicle routing problem with path flexibility[J]. Transportation

Research Part B：Methodological，2017，95：169-195.

[7] FARO A，GIORDANO D. Algorithms to find shortest and alternative paths in free flow and congested traffic regimes- ScienceDirect[J]. Transportation Research Part C： Emerging Technologies，2016，73：1-29.

[8] 楊兆升. 城市交通流诱导系统理论与模型[M]. 北京：人民交通出版社，2000.

YANG Z S. Theory and model of urban traffic flow induction system[M]. Beijing：China Communication Press，2000.

[9] FU L P，RILETT L R. Expected shortest paths in dynamic and stochastic traffic networks[J]. Transportation Research Part B：Methodological，1998，32（7）：499-516.

[10] 段宗涛，WANG W X，康军，等. 面向城市交通网络的K最短路径集合算法[J]. 交通运输系统工程与信息，2014，14（3）：194-200.

DUAN Z T，WANG W X，KANG J，et al. K shortest path set algorithm for urban traffic network[J]. Journal of

Transportation Systems Engineering and Information Technology，2014，14（3）：194-200.

[11] HU X，CHIU Y C. A constrained time-dependent K shortest paths algorithm addressing overlap and travel time deviation[J]. International Journal of Transportation Science & Technology，2015，4（4）：371-394.

[12] MORI U，MENDIBURU A，ALVAREZ M，et al. A review of travel time estimation and forecasting for advanced traveller information systems[J]. Transportmetrica，2015，11（1/2）：119-157.

[13] SUN L，YANG J，MAHMASSANI H. Travel time estimation based on piecewise truncated quadratic speed trajectory[J]. Transportation Research Part A Policy & Practice，2008，42（1）：173-186.

[14] 潘义勇. 动态随机交通网络环境下耗时最可靠路径研究[D]. 南京：东南大学，2014.

PAN Y Y. Study on the optimal-reliable routing in stochastic and dynamic traffic network[D]. Nanjing：Southeast University，2014.

[15] ICHOUA S，GENDREAU M，POTVIN J Y. Vehicle dispatching with time-dependent travel times[J]. European

Journal of Operational Research，2003，144（2）：379-396.

[16] 郑长江，陈宜恒，沈金星. 基于地铁的地上地下闭环物流配送路径优化[J]. 华东交通大学学报，2022，39（1）：89-98.

ZHENG C J，CHEN Y H，SHEN J X. Distribution routing optimization of ground-underground closed-loop logistics based on metro network[J]. Journal of East China Jiaotong University，2022，39（1）：89-98.

[17] 徐涛，丁晓璐，李建伏. K最短路径算法综述[J]. 计算机工程与设计，2013，34（11）：8.

XU T，DING X L，LI J F. Review on K shortest paths algorithm[J]. Computer Engineering and Design，2013，34（11）：8.

[18] 李臣波. 網络的K最短路算法研究[D]. 哈尔滨：哈尔滨理工大学，2008.

LI C B. Algorithm rearch on K shortest path of networks[D]. Harbin： Harbin University of Science and Technology，2008.