基于压缩库产生的磁子阻塞

李明翠 陈爱喜 曾伟

摘要：基于近年来微波腔与磁子相互作用的实验进展以及非线性库理论，提出将腔-磁系统与压缩库耦合，分析其中的磁子阻塞效应，以实现磁性量子级的操控。在一个受驱动的微波腔中放置一个钇铁石榴石小球，球体中的Kittel模与微波腔模耦合，同时腔场与压缩真空库耦合。通过数值求解系统的量子主方程，详细分析了关联函数受耦合强度、失谐量、耗散率等因素的影响。从理论上证明了与压缩库耦合的腔-磁系统可以产生单磁子阻塞和双磁子阻塞，并且可以通过调节驱动强度或者失谐量灵活地在单磁子阻塞、双磁子阻塞、双磁子隧穿之间进行切换。所提出的磁子阻塞方案主要由压缩库的非线性诱导得到，为腔-磁系统实现单磁子和双磁子阻塞提供了一种可能的新途径。

关键词：磁子;阻塞;压缩库;微波腔

中图分类号：O413.2 文献标志码：A

本文引用格式：李明翠，陈爱喜，曾伟. 基于压缩库产生的磁子阻塞[J]. 华东交通大学学报，2023，40（1）：99-105.

Magnon Blockade Generated by Coupling to a Squeezed Reservoir

Li Mingcui1，Chen Aixi2，Zeng Wei1

（1. School of Information Engineering， East China Jiaotong University， Nanchang 330013， China;

2. School of Science， Zhejiang Sci-Tech University， Hangzhou 310018， China）

Abstract：Inspired by the recent experiments of cavity-magnon system and the theories of nonlinear reservoir， a scheme of coupling a cavity-magnon system to a squeezed reservoir is proposed to analyze the magnon blockade effect， thus realizing the manipulation of magnetism at quantum level. An yttrium iron garnet sphere was located in a driven microwave cavity. The Kittel mode in the yttrium iron garnet sphere interacted with the microwave cavity mode， and the cavity field was coupled to a squeezed vacuum reservoir. By numerically solving the quantum master equation of the system， the influence of various factors such as coupling strength， detuning and dissipation rate on the correlation function was analyzed in details. It is proved theoretically that the cavity-magnon system coupled to a squeezed reservoir can induce single-magnon blockade and two-magnon blockade， and the switching among single-magnon blockade， two-magnon blockade and two-magnon tunneling can be flexibly controlled by tuning the driving intensity or the detuning. The magnon blockade effect in the proposed scheme is mainly induced by the nonlinearity of the squeezed reservoir， which provides a possible new method to realize single or double magnon blockade in cavity-magnon system.

Key words： magnon; blockade; squeezed reservoir; cavity

Citation format：LI M C，CHEN A X，ZENG W. Magnon blockade generated by coupling to a squeezed reservoir[J]. Journal of East China Jiaotong University，2023，40（1）：99-105.

磁子是量子化的自旋波，具有能量耗散率低、體积小[1-2]等优点，可用于新型的基于波的计算技术中。钇铁石榴石（YIG）具有极高的自旋密度，是量子信息处理领域很有潜力的磁性材料[2-3]。YIG球体中的Kittel模与微波腔中的场模在低温和室温下都实现了强耦合[4-6]，甚至超强耦合[7]。通过微波腔中虚光子的激发，YIG小球中的磁子与transmon类型的量子比特之间的相互作用已得到了实验证实[8]。

磁子阻塞是制备磁子源的基础。在包含一个量子比特和一个YIG小球的腔-磁系统中，磁子阻塞于2019年首次被提出[9]，随后的相关研究也陆续展开[10-11]。同时，在三明治夹层结构的磁子节中，也展现了依赖于自旋的磁子阻塞效应[12]。理论上，光子、声子和磁子的同时阻塞可以在包含YIG球体和二能级原子的光-力-磁系统中实现[13]。与磁子阻塞相关的研究还包含宇称时间对称的腔-磁系统中的磁子阻塞[14]，纳米磁体中的磁子反聚束效应[15]，腔-磁系统中的克尔效应导致的磁子亚泊松统计等[16]。

以上这些磁子阻塞相关的工作都是基于将非线性系统（系统中包含二能级原子、光力非线性作用或Kerr非线性等）耦合到一个谐振库（通常是热库）的模型。事实上，通过耦合到压缩库，许多光学性质，如稳态行为[17]、纠缠和压缩[18-19]、反聚束和光子阻塞[20-22]都得到了研究。基于这些理论和相关的磁子实验，本文首次提出将一个线性的腔-磁系统耦合到压缩库，讨论其中的磁子阻塞效应。

1 系统模型

考虑图1所示的系统模型，一个YIG小球放置在微波腔中。YIG小球中的磁模与腔模强耦合，其中磁子的频率可以通过外加偏置磁场进行调节。该微波腔由单模相干光驱动，并与压缩库耦合。在驱动场频率的旋转框架中，微波腔和YIG小球这部分的哈密顿量如式（1）所示

H

?=Δaa?a+Δmm?m+Km?mm?m+

g（am?+a?m）+ε（a+a?）    （1）

式中：a（a?）和m（m?）分别为腔模和磁模的湮灭（产生）算符;Δj=ωj-ωd（j=a，m）为失谐量，ωj（j=a，m）为这些模式的频率;?为约化普朗克常量;磁模的频率可以从外部偏置磁场Hm和相应的旋磁比γ得到，即 ωm=γHm[23];Km?mm?m为YIG材料中磁晶各向异性引起的克尔项[24-25]，K为克尔系数;g为谐振腔中磁模与微波场之间的耦合强度;ε为驱动场和腔模之间的耦合强度。

在弱驱动条件下，系统的能级可以在截断的Fock空间中进行分析。考虑总激发数N≤2的情况，可以得到式（1）中哈密顿量的裸态，即 |00〉，|01〉，

|10〉，|11〉，|02〉和|20〉。在态|n1n2〉中，n1为微波光子数，n2为磁子数。在以这些裸态为基的空间中，式（1）中无驱动的哈密顿量可以展开成式（2）的矩阵形式[14，26]

=0 0      00           0       0

0 Δm+K g0           0       0

0 g      Δa 0           0       0

0 0      0Δa+Δm+K

g

g

0 0      0

g     2Δm+4K 0

0 0      0

g     0        2Δa（2）

設Δa=Δm=0，可以得到式（3）～式（6）的系统本征值。

E0=0 （3）

E1±=             （4）

E20=    （5）

E2±=  （6）

式中：θ=arccosT，T=，

对K和g进行适当的取值，系统的能谱可以表现出非谐性。然而，当克尔系数远小于耦合强度时，系统能级的非谐性消失了。即，如果K→0，式（4）、式（5）和式（6）的特征值变为E1±=±g，E20=-2g，E2±=+2g。事实上，在目前的实验条件下，获得的克尔系数通常非常小（直径为1 mm的YIG小球中观测到的Kerr系数约为10-10Hz[23-25]）。因此，腔-磁振系统本身不足以产生磁子阻塞。

假设微波腔与压缩库耦合。系统的动力学演化由式（7）所示的主方程控制[19，22，27-28]

=-i[H，ρ]-Na[aa?ρ-2a?ρa+ρaa?]-

（Na+1）[a?aρ-2aρa?+ρa?a]-

[m?mρ-2mρm?+ρm?m]+

[aaρ-2aρa+ρaa]+

[a?a?ρ-2a?ρa?+ρa?a?]   （7）

式中：H为式（1）所示的系统哈密顿量;γa（γm）为腔模（磁模）的耗散率;Na为压缩库中频率为ωa的平均光子数;Ma为压缩参数。参数Na和Ma满足不等式Ma≤。

磁子的统计特性可以用关联函数描述[9-10]。二阶关联函数的定义如式（8）所示

g（2）（τ）=  （8）

式中：τ为两个磁子之间的延迟时间。与光子和声子阻塞类似，单磁子阻塞可以用具有亚泊松统计特性的等时（τ=0）二阶关联函数g（2）（0）<1来表征。g（2）（0）>1对应于具有超泊松统计特性的双磁子群

聚束（双磁子隧穿）效应。好的单磁子源还应当满足式（9）中的条件[22]

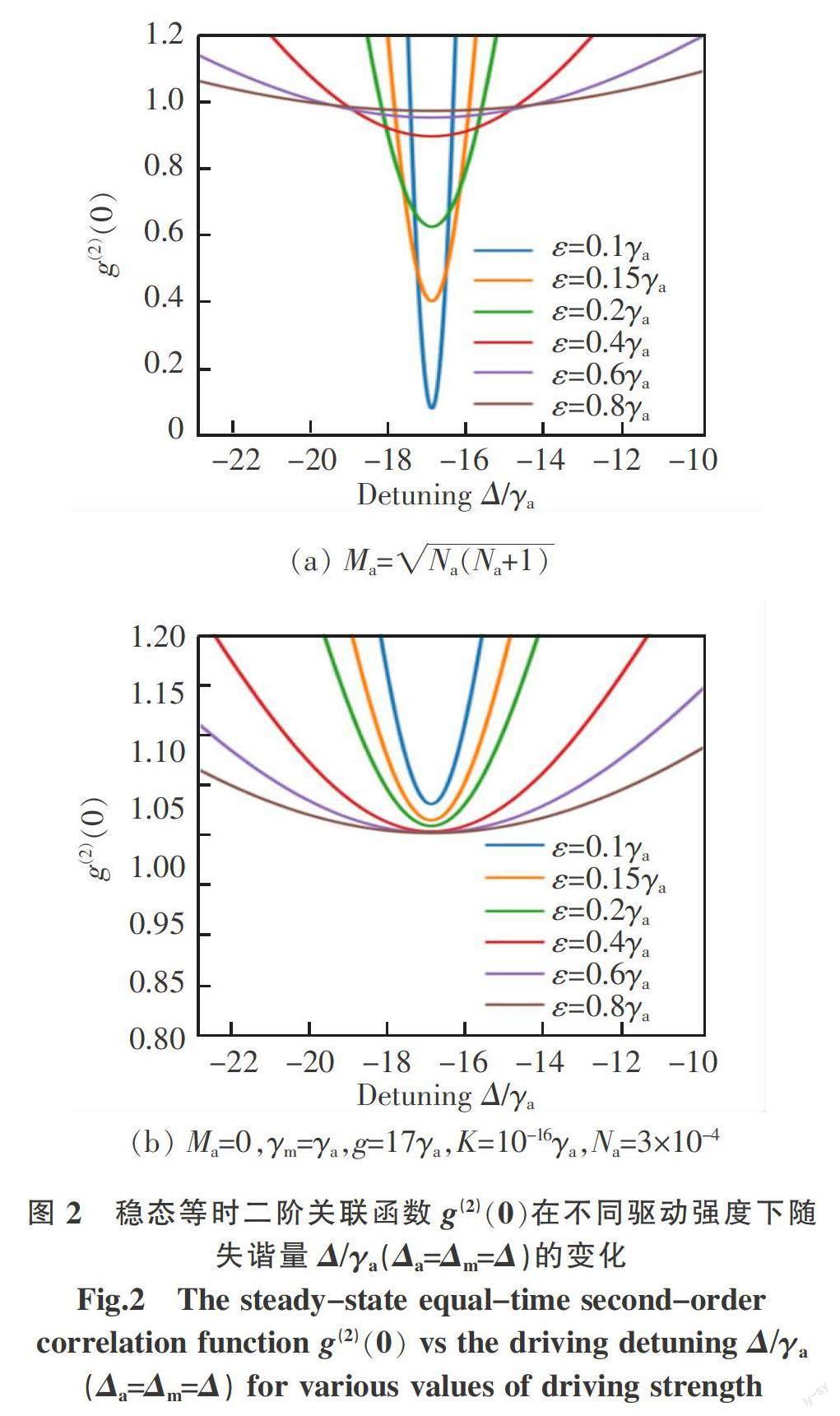
g（3）（0）

多磁子阻塞可以用k阶关联函数 gk（0）=〈（a?）k（a）k〉

〈a?a〉k来表征。在少量磁子数的条件下，多磁子阻塞的判断标准可简化为式（10）[22，29-30]

gk（0）≥1 and g（k+1）（0）<1   （10）

2 数值模拟计算

本节通过数值求解式（7）中的主方程，讨论系统参数对关联函数的影响。数值模拟结果使用Python软件包QUTIP[31]计算获得，所有参数的选取均基于目前的实验进展。

图2展示了耦合库有压缩（图2（a））和无压缩（图2（b））两种情形下，等时二阶关联函数g（2）（0）随腔模相对于驱动场的失谐量的变化。这里克尔系数设置为K=10-16γa，即假设使用的是直径约为1 mm的YIG小球。

在弱驱动限制条件下，克尔非线性对毫米直径的YIG小球的量子统计结果几乎没有影响。然而，在纳米直径的YIG小球中情况并非如此，这将在图3中讨论。如图2（a）所示，通过调整驱动强度ε，可以获得满足g（2）（0）<1的关联函数值。对于图2（a）给定的参数，随着驱动强度从0.1γa增加到0.8γa，不同曲线的最小值从0.076 1增加到1，并且反聚束效应在ε≥0.8γa时消失。图2中的所有曲线均关于直线Δ≈-17γa=-g对称，并且g（2）（0）的最小值位于对称轴上。在图2（b）中，系统与非压缩的普通库耦合，即Ma=0。在这种情况下，系统的非线性完全由克尔效应决定。然而，对于毫米直径的YIG小球而言，克尔系数太弱，不足以诱导磁子反聚束效应。

事实上，克尔系数（K=μ0kanγ2/（M2V））与YIG球体的体积成反比[24-25]，其中kan，γ，M和V为一阶各向异性常数、旋磁比、饱和磁化强度和YIG球体的体积，μ0为真空磁导率。另一方面，微波光子-磁子耦合强度g与YIG球体中的自旋数的平方根成正比，即g=g0=g0，S为YIG球体的净宏观自旋数、ρ为净自旋密度，g0（g0 /2π=38 mHz）为单个玻尔磁子与微波空腔的耦合强度[5，25]。因此，g随YIG小球体积的减小而减小，而克尔系数随球体体积的减小而增大。假设直径为1 mm的YIG小球中的磁膜与微波腔模的耦合强度为g=17γa，克尔系数为K=10-16γa，可以进一步计算出不同直径的YIG小球相应的耦合强度和克尔系数。当YIG小球的直径大于0.3 μm时，耦合强度远远大于克尔系数。假设微波腔的耗散率为γa /2π=2.7 MHz[5]，随着YIG小球直径减小到0.2 μm，克尔系数增加到大约212.058 Hz，同时耦合强度降低到大约815.713 Hz。当YIG小球的直径减少到只有几纳米时，克尔效应比腔模和磁模之间的相互作用要强得多。在这种情况下，腔模-磁模相互作用以及与压缩库的耦合不再是产生磁子阻塞的必要条件。通过直接驱动非线性纳米磁体，就可以获得主要由纳米磁体的克尔非线性引起的磁子的反聚束效应[15]。YIG小球的尺寸对二阶关联函数的影响如图3所示，参数设置为γm=γa，ε=0.1γa，Na=3×10-4，Ma=，并假设直径为1 mm的YIG球的腔模-磁模耦合强度和克尔系数为g=17 γa，K=10-16 γa。不同直径d=（0.5 mm，0.3 mm，0.1 mm，10 μm，）对应的g（2）（0）的最小值分别位于（Δ≈

-6.005γm，g≈6.010γm），（Δ≈-2.790γm，g≈2.793γm），（Δ≈-0.533γm，g≈0.538γm），（Δ≈-0.015γm，g≈0.017γm）。此时，g相对于Δ的比率大约等于-1。然而，当直径小于0.1 μm时，g/Δ的绝对值远小于1，此时克尔非线性效应比腔模-磁模之间的相互作用强得多，在诱导磁子反聚束效应中起到更重要的作用。

与光子源类似，一个好的单磁子源对应的关联函数值应该满足不等式条件g（3）（0）

g（2）（0），g（3）（0），g（4）（0）在弱驱动下随驱动强度的ε/γa变化。曲线g（2）（0）和g（3）（0）在点（ε，g（2）（0））≈（0.129，0.285）处相交。在图4给出的条件下，当驱动强度大于或等于0.13γa时，系统可以很好地满足式（9）表示的良好单磁子源的要求。图5绘制了延时二阶关联函数g（2）（τ）随γaτ的变化，以进一步验证系统是否满足“真”单磁子阻塞条件，相关参数为g=17γa，γm=γa，Δa=Δm=-g，Na=3×10-4，Ma=

，K=10-16γa。显然，在给定的条件下，当驱动强度处于[0.13γa，0.14γa]区间时，系统同时满足“好”单磁子源条件和“真”单磁子阻塞标准。

为了讨论本系统产生双磁子阻塞的可能性，图6绘制了关联函数g（k）（0）在不同驱动强度下随磁子耗散率γm /γa和失谐量Δ/γa的变化，在图6（a）中，g=17γa，Δa=Δm=-g，K=10-16γa;在图6（b）中，g=17γa，γm=0.5γa，K=10-16γa;图6（c）中，g=0.5γa，Δa=Δm=-g，K=10-13γa;在图6（d）中，g=0.5γa，γm=0.5γa，K=10-13γa。其他参数为Na=3×10-4，Ma=。图中的不同关联函数通过颜色和线型进行区分：实线（虚线）表示等时二阶（三阶）关联函数g（2）（0）（g（3）（0）），红色（绿色、蓝色）表示3种不同的驱动强度ε=1γa（2γa，3γa）。阴影区域是在不同条件下获得的双磁子阻塞窗口：图6（a）和图6（c）中的第一个窗口在ε=2γa，条件下获得，第二个窗口在ε=3γa条件下获得;图6（b）中的左侧和右侧窗口在ε=3γa条件下获得;图6（b）中间的窗口和图6（d）的窗口在ε=2γa条件下获得。本文采用判据g（2）（0）≥1且g（3）（0）<1判定双磁子阻塞，用条件1

可以得到g（3）（0）<1

3 结论

本文提出了一种通过将腔-磁系统耦合到压缩库来操控磁子阻塞效应的方案。文章通过数值求解量子主方程，分析了磁子的統计性质，详细讨论了磁子关联函数受外部驱动强度、失谐量、耗散率等因素的影响。所提出的方案无论是工作在微波腔与YIG小球Kittel模相互作用的强耦合区还是弱耦合区域，都可以满足“好”单磁子源和“真”单磁子阻塞的标准。当微波腔的驱动强度略强于微波腔的耗散率时，还可以观测到双磁子阻塞窗口。系统中的磁子阻塞效应主要是由所耦合的量子压缩库导致的，而不是由腔-磁系统本身的非线性特性引起的。这为实现磁子阻塞提供了一种可能的新途径，在基于混合腔-磁系统平台的量子系统中有潜在的作用。

参考文献：

[1] CHUMAK A V，VASYUCHKA V I，SERGA A A，et al. Magnon spintronics[J]. Nature Physics，2015，11（6）：453-461.

[2] SERGA A A，CHUMAK A V，HILLEBRANDS B. YIG magnonics[J]. Journal of Physics D：Applied Physics，2010，43（26）：264002.

[3] KONG C，BAO X M，LIU J B，et al. Magnon-mediated nonreciprocal microwave transmission based on synthetic magnetic flux[J]. Optics Express，2021，29（16）：25477.

[4] ZHANG X，ZOU C L，JIANG L，et al. Strongly coupled magnons and cavity microwave photons[J]. Physical Review Letters，2014，113（15）：156401.

[5] TABUCHI Y，ISHINO S，ISHIKAWA T，et al. Hybridizing ferromagnetic magnons and microwave photons in the quantum limit[J]. Physical Review Letters，2014，113（8）：083603.

[6] ZHANG D，WANG X M，LI T F，et al. Cavity quantum electrodynamics with ferromagnetic magnons in a small yttrium-iron-garnet sphere[J]. Npj Quantum Information，2015，1（1）：15014.

[7] BOURHILL J，KOSTYLEV N，GORYACHEV M，et al. Ultrahigh cooperativity interactions between magnons and resonant photons in a YIG sphere[J]. Physical Review B，2016，93（14）：144420.

[8] TABUCHI Y，ISHINO S，NOGUCHI A，et al. Coherent coupling between a ferromagnetic magnon and a superconducting qubit[J]. Science，2015，349（6246）：405-408.

[9] LIU Z X，XIONG H，WU Y. Magnon blockade in a hybrid ferromagnet-superconductor quantum system[J]. Physical

Review B，2019，100（13）：134421.

[10] XIE J K，MA S L，LI F L. Quantum-interference-enhanced magnon blockade in an yttrium-iron-garnet sphere coupled to superconducting circuits[J]. Physical Review A，2020，101（4）：042331.

[11] XU Y J，YANG T L，LIN L，et al. Conventional and unconventional magnon blockades in a qubit-magnon hybrid quantum system[J]. Journal of the Optical Society of America B，2021，38（3）：876-884.

[12] YAN Z R，WAN C H，HAN X F. Magnon blocking effect in an antiferromagnet-spaced magnon junction[J]. Physical

Review Applied，2020，14（4）：044053.

[13] ZHAO C，LI X，CHAO S，et al. Simultaneous blockade of a photon，phonon，and magnon induced by a two-level atom[J]. Physical Review A，2020，101（6）：063838.

[14] WANG L，YANG Z X，LIU Y M，et al.  Magnon blockade in a PT-symmetric-like cavity magnomechanical system[J]. Annalen der Physik，2020，532（7）：2000028.

[15] YUAN H Y，DUINE R A. Magnon antibunching in a nanomagnet[J]. Physical Review B，2020，102（10）：100402.

[16] HAGHSHENASFARD Z，COTTAM M G. Sub-Poissonian statistics and squeezing of magnons due to the Kerr effect in a hybrid coupled cavity-magnon system[J]. Journal of Applied Physics，2020，128（3）：033901.

[17] JOSHI A，PURI R R. Steady-state behavior of three-level systems in a broadband squeezed bath[J]. Physical Review A，1992，45（3）：2025-2030.

[18] MOSISA E，WIMBERGER S. Enhanced squeezing and entanglement in nondegenerate three-level laser coupled to squeezed vacuum reservoir[J]. Advances in Mathematical

Physics，2021（2021）：6625690.

[19] TAN H T，GAN Z W，LI G X. Entanglement for excitons in three quantum dots in a cavity coupled to a broadband squeezed vacuum[J]. Acta Physica Sinica，2004，54（3）：1179-1183.

[20] LEMONDE M A，DIDIER N，CLERK A A. Antibunching and unconventional photon blockade with Gaussian squeezed states[J]. Physical Review A，2014，90（6）：063824.

[21] MIRANOWICZ A，BAJER J，PAPRZYCKA M，et al. State-dependent photon blockade via quantum-reservoir engineering[J]. Physical Review A，2014，90（3）：033831.

[22] KOWALEWSKA-KUDASZYK A，ABO S I，CHIMCZAK G，et al. Two-photon blockade and photon-induced tunneling generated by squeezing[J]. Physical Review A，2019，100（5）：053857.

[23] LI J，ZHU S Y，AGARWAL G S. Magnon-photon-phonon entanglement in cavity magnomechanics[J]. Physical Review Letters，2018，121（20）：203601.

[24] WANG Y P，ZHANG G Q，ZHANG D，et al. Magnon kerr effect in a strongly coupled cavity-magnon system[J].

Physical Review A，2016，94（22）：224410.

[25] ZHANG G Q，WANG Y P，YOU J Q. Theory of the magnon Kerr effect in cavity magnonics[J]. Science China Physics， Mechanics & Astronomy，2019，62（8）：987511.

[26] 張智明. 量子光学[M]. 北京：科学出版社，2014：145-146.

ZHANG Z M. Quantum optics[M]. Beijing：China Science

Publishing & Media Ltd，2014：145-146.

[27] SCULLY M O，ZUBAIRY M S. Quantum Optics[M]. Cambridge：Cambridge University，1997.

[28] DUM R，PARKINS A S，ZOLLER P，et al. Monte carlo simulation of master equations in quantum optics for vacuum，thermal，and squeezed reservoirs[J]. Physical Review A，1992，46（7）：4382-4396.

[29] HAMSEN C，TOLAZZI K N，WILK T，et al. Two-photon blockade in an atom-driven cavity QED system[J]. Physical

Review Letters，2017，118（13）：133604.

[30] ZHAI C，HUANG R，JING H，et al. Mechanical switch of photon blockade and photon-induced tunneling[J]. Optics Express，2019，27（20）：27649-27662.

[31] JOHANSSON J R，NATION P D，NORI F. QuTiP：A Python framework for the dynamics of open quantum systems[J]. Computer Physics Communications，2013，184（4）：1234-1240.