二维光子晶体带隙与结构的关系

陈义万 ,杜海霞 ,陈昭蓉 ,闵锐

(1.湖北工业大学理学院，湖北 武汉 430068；2.火箭军工程大学理学院，陕西 西安 710025:3.广西大学计算机与电子信息学院，广西 南宁 530003)



二维光子晶体带隙与结构的关系

陈义万1,杜海霞2,陈昭蓉3,闵锐1

(1.湖北工业大学理学院，湖北 武汉 430068；2.火箭军工程大学理学院，陕西 西安 710025:3.广西大学计算机与电子信息学院，广西 南宁 530003)

摘要：用时域有限差分法(FDTD)及完全匹配层边界条件(PML)，计算由介质圆柱构成正方形格子排列的二维光子晶体对光的透射谱，分别得到完整正方格子晶体、中间有孔的正方格子晶体的透射率随波长的变化关系，发现对正方形格子排列的二维光子晶体，移去中间部分的圆柱形成口字型孔时，得到该结构在波长0.280.60 μm的范围内，光的透着率有1个平坦的极小值区间，对应的能量为2.074.44 eV，带隙宽度为ΔE=2.37 eV.与中间为十字形孔的结构相比，口型孔的结构可以得到较理想的带隙.

关键词：光子晶体；二维；带隙；FDTD ；PML

0引言

光子晶体[1-2]是由折射率为n的介质，在三维空间中周期性排列形成的，本文中的背景介质为空气.为研究光子晶体中光的传播性质，我们把它与传统的晶体结构进行对比.对于由原子周期性排列形成的晶体结构，电子在晶体中运动时，满足薛定谔方程[3]:

(1)

其中，V(r)是电子在晶体中运动的势能函数.

当光在光子晶体中传播时，遵守电磁场的Maxwell方程，经过化简，得到电场E满足的亥姆霍兹方程[4]：

(2)

其中n为折射率，k为电磁波在真空中的波矢的大小.

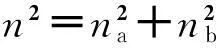
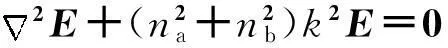
(3)

比较(1)式与(3)式，它们具有类似的形式，其解也具有相似的性质.电子在晶体中运动时，会形成能带结构，存在禁带.类似地，电磁波在光子晶体中传播时，也会存在带隙，波长在带隙范围的电磁波，在光子晶体中不能传播.

1时域有限差分法(FDTD)

时域有限差分法(FDTD)由KSYee在1966年提出[5]，在计算物理中得到广泛应用.其基本思想是把数学中的微分用差分代替，用中心差分法表达导数为[6]：

由于计算机的储存容量的限制，计算的物理区间有限，用FDTD方法计算时，广泛使用的是完全匹配吸收层边界条件(PML)[7].通过选择边界内的电导率和磁导率的比值：

使电磁波从介质入射到边界后被完全吸收，不被反射.

用FDTD方法推导的2维TE模式的电磁波递推表达式为：

2由圆柱介质构成的2维正方形格子的透射谱

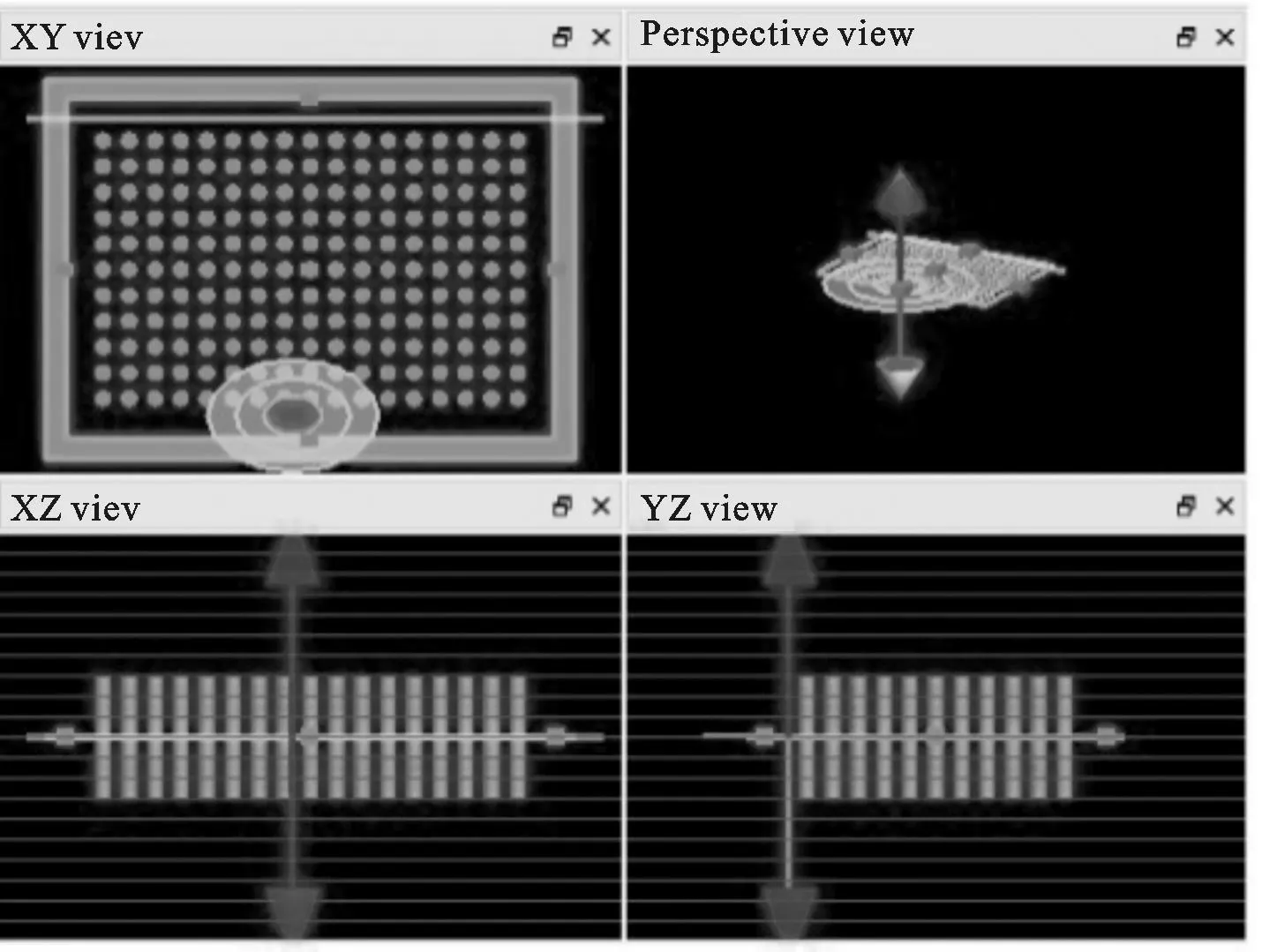
图1　17×11阵列二维光子晶

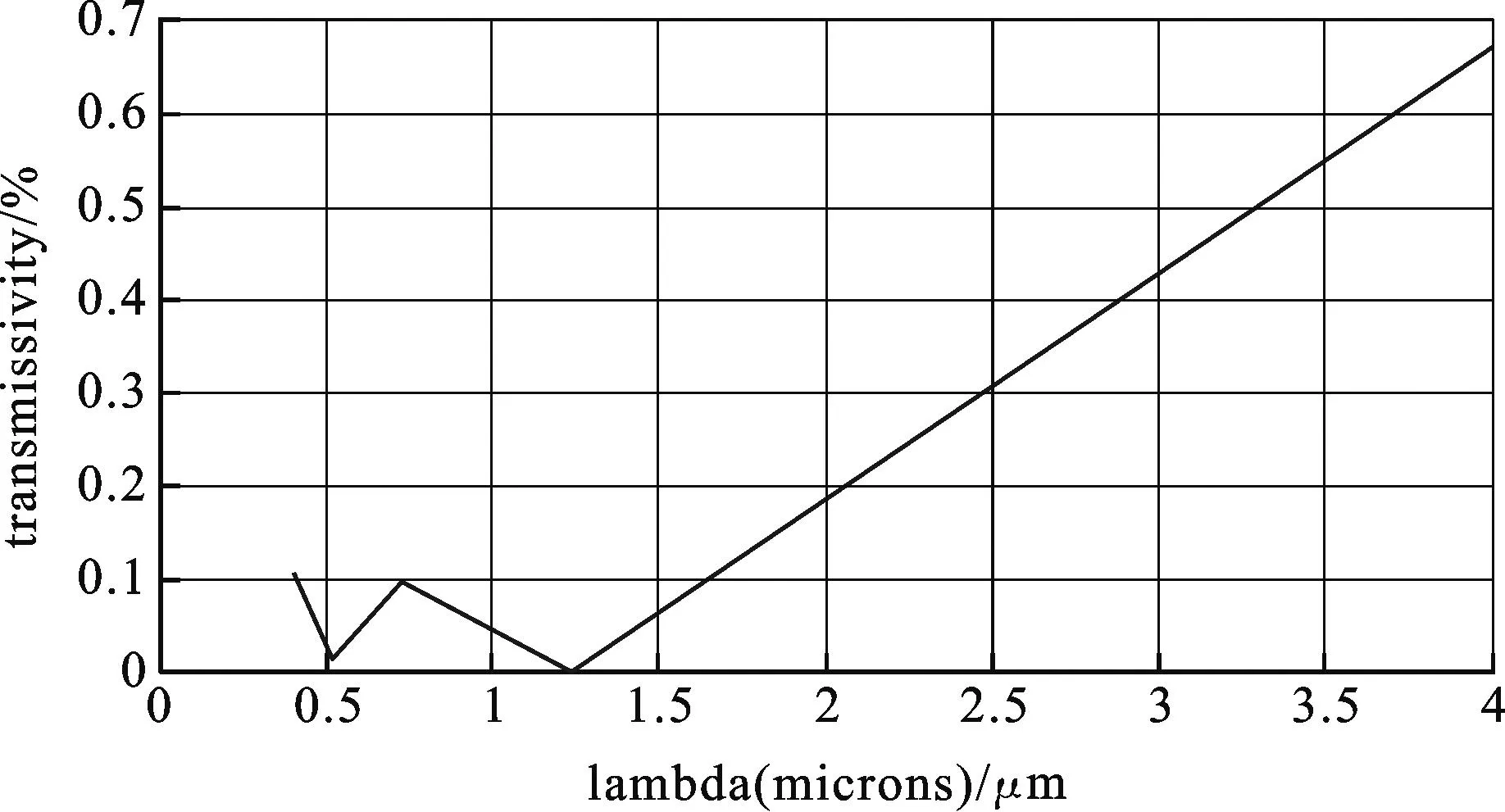
图2　17×11阵列二维光子晶体的透射率与波长的关

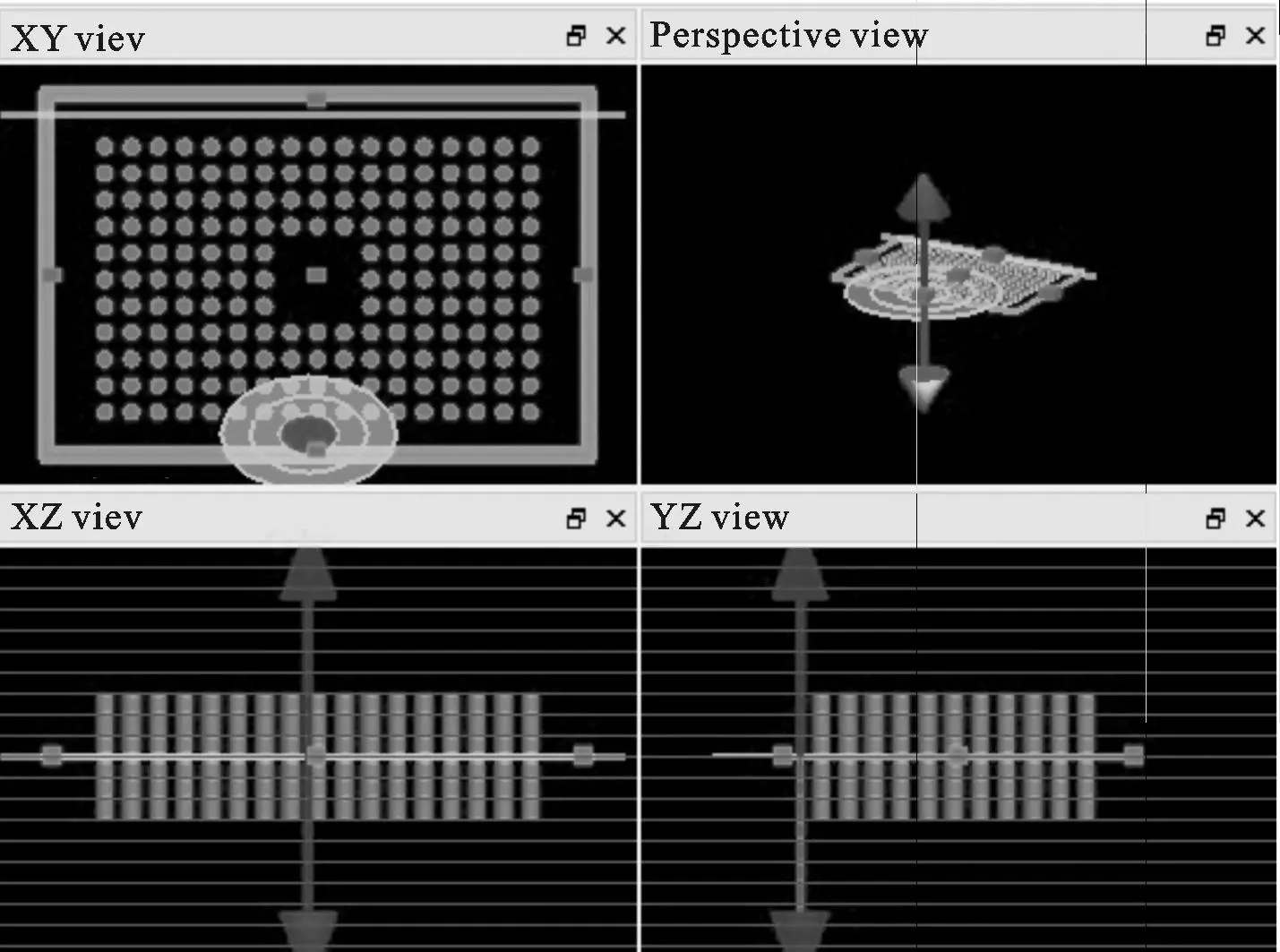
图3　中间为3×3口字型孔的17×11阵列二维光子晶

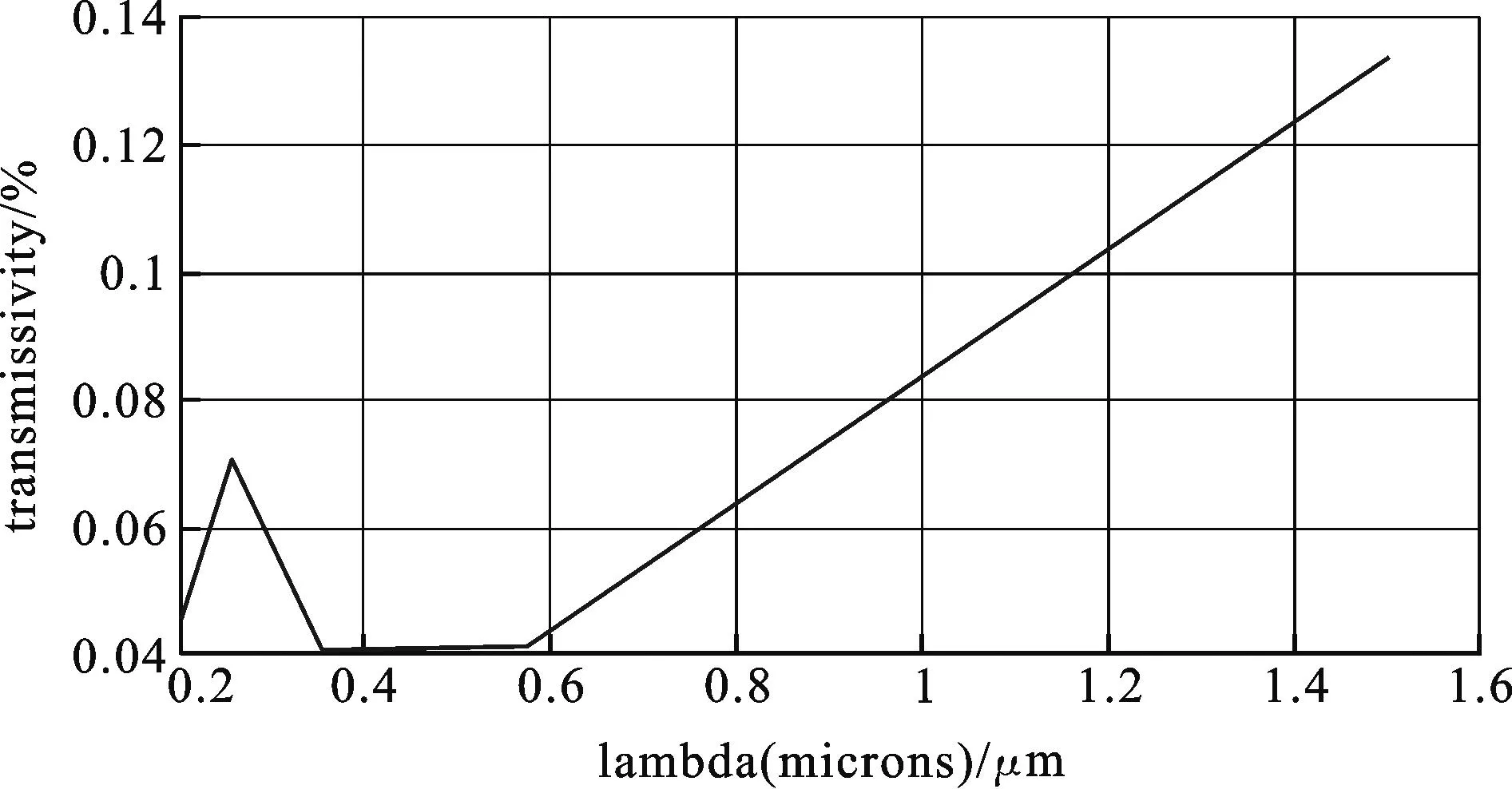
图4　中间为3×3口字型孔的17×11阵列二维光子晶体的透射率与波长的关

从图6中可以看出，该结构在λ1=0.50μm和λ2=1.30μm处各有透射率极小值，该透射率图与完整光子晶体结构的透射率图非常相似.

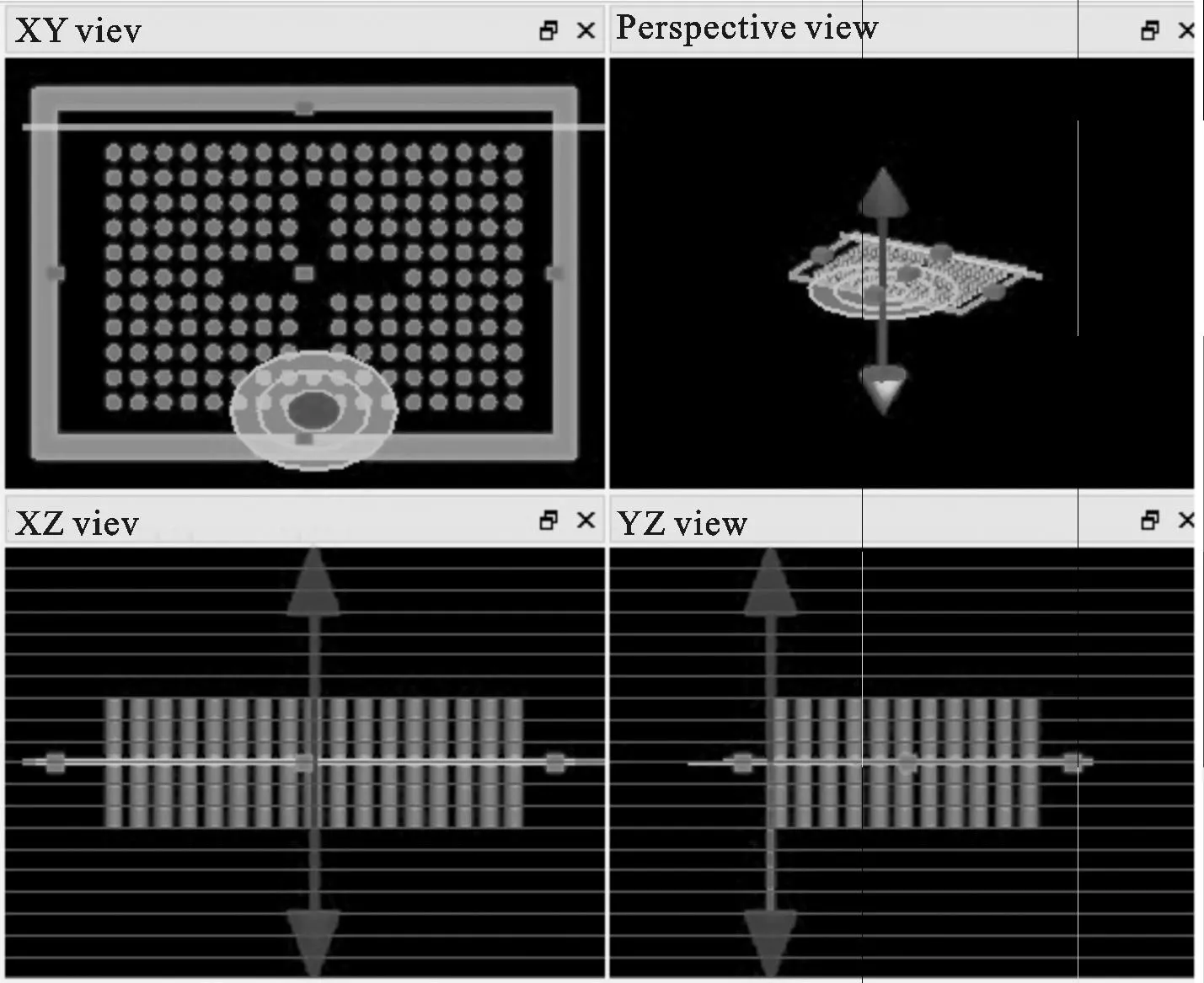
图5　中间为十字型孔的17×11阵列二维光子晶

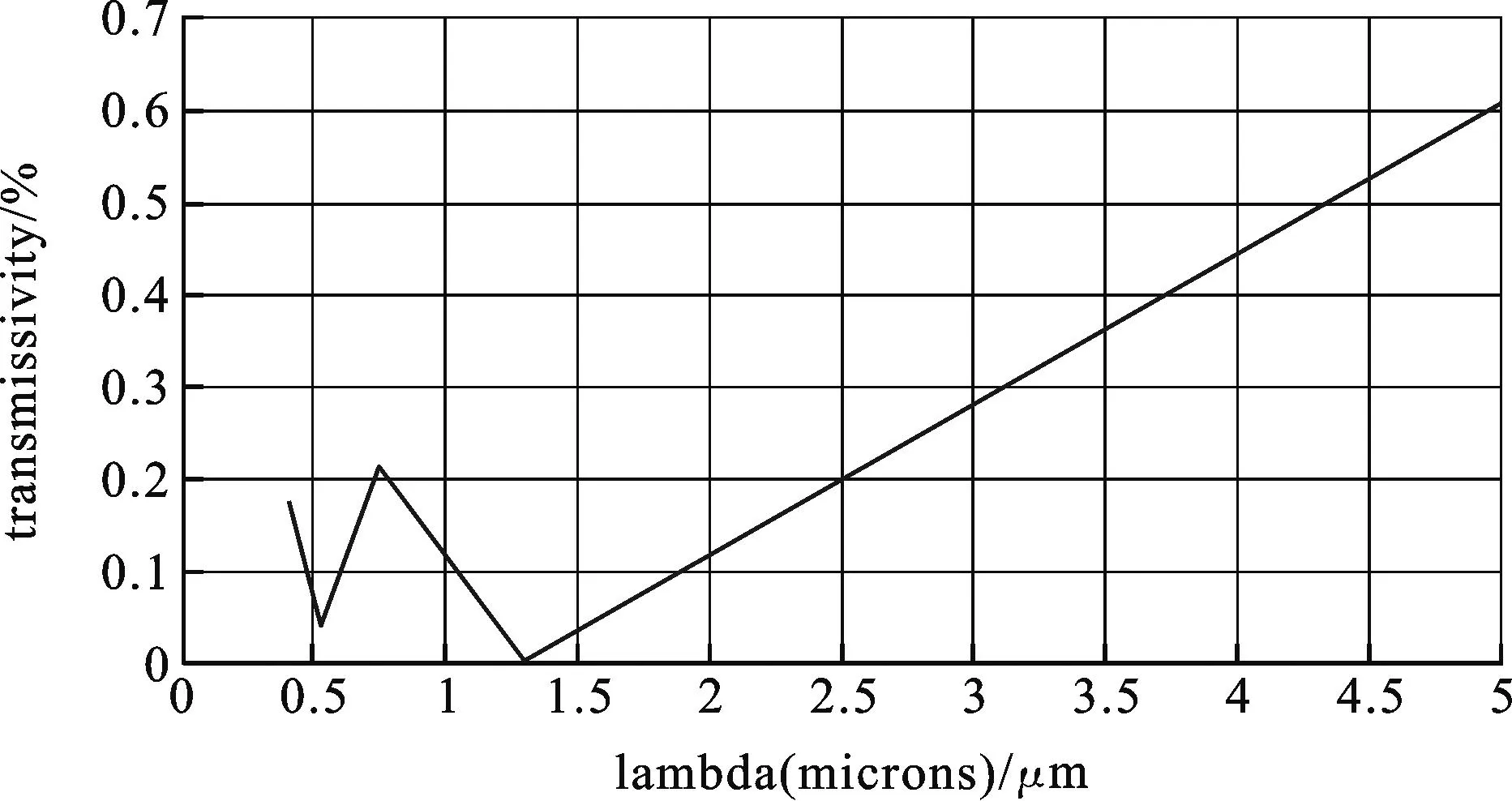
图6　中间为十字型孔的17×11阵列二维光子晶体透射率与波长的关

3结论

4参考文献

[1] JOHN S.Strong localization of photons in certain disordered dielectric lattice[J].Phys Rev Lett，1987,58(23)：2486-2489.

[2] YABLONOVITCH E.Inhibited spontaneous emission in solid state physics and electronics[J] Phys Rev Let，1987,58(20):2059-2061.

[3] 曾谨言.量子力学：卷1[M].3版.北京：科学出版社，2000:77.

[4] 吴重庆.光波导理论[M].2版.北京：清华大学出版社，2005:6.

[5] Yee K S.Numerical solution of initial boundary value problems involving Maxwell equations in isotropic medie[J].IEEE Trans Antennas Propagate，1966，14(3):302-307.

[6] 葛德彪，阎玉波.电磁波时域有限差分方法[M].3版.西安:西安电子科技大学出版社,2011:10.

[7] 崔俊海,钟顺时.采用PML吸收边界条件的FDTD法在分析平面微带结构中的应用[J].微波学报，2000,16(20):537-541.

[8] 梅洛勤，叶卫民.用传输矩阵法(TMM)研究二维光子晶体的传输特性[J].量子光学学报，2003，9(2)：88-92.

(责任编辑郭定和)

The relationship of two- dimensional photonic crystal band gap with its structure

CHEN Yiwan1,DU Haixia2,CHEN Zhaorong3,MIN Rui1

(1.School of Science,Hubei University of Technology,Wuhan 430068,China;2.School of Science,The Rockets Army Engineering University,Xi’an 710025,China;3.School of Computer and Electronic Information,Guangxi University,Nanning 530003,China)

Abstract:The article used finite difference time domain (FDTD) method and perfectly matched layer (PML) boundary condition,and calculated light transmission of the cylindrical dielectric forming a two-dimensional photonic crystal of square lattice,found the two-dimensional photonic crystal of square lattice removed the middle part of the cylinder(mouth cavity structure),within the scope of 0.28 μm to 0.6 μm,has a flat minimum interval,the corresponding energy is 2.07 eV to 4.44 eV,the band gap width is ΔE = 2.37 eV.Compared with the middle cross hole structure,mouth cavity structure can get ideal band gap.

Key words:photonic crystal; two-dimension; band gap; FDTD; PML

中图分类号:O431

文献标志码:A

DOI:10.3969/j.issn.1000-2375.2016.03.009

文章编号:1000-2375(2016)03-0220-04

作者简介：陈义万(1965-)，男，副教授，E-mail:chenyiwan@yeah.net

基金项目：湖北省教育科学“十二五”规划重大项目(2012A016)资助

收稿日期:2015-12-08