磁化强度调制的圆柱形纳米线磁子晶体*

王梦宁，李志雄，唐　伟，聂耀庄，郭光华

(中南大学 物理与电子学院,长沙 410083)



磁化强度调制的圆柱形纳米线磁子晶体*

王梦宁，李志雄，唐伟，聂耀庄，郭光华

(中南大学 物理与电子学院,长沙 410083)

摘要：采用微磁学模拟的方法研究了自旋波在磁化强度周期变化的圆柱形纳米线中的传播特性。结果显示，频谱和色散关系图中均能看到明显的自旋波通带和禁带。带隙是由自旋波在布里渊区边界处的布拉格反射引起的。通过改变磁子晶体的周期长度、磁化强度比值可以有效的调制自旋波带隙结构。当周期长度增大时，带隙数目增加，带隙频率位置降低，带隙宽度变窄。随着磁化强度调制的增强，带隙位置逐渐降低，而带隙宽度表现出复杂的变化形式，有些带隙表现出振荡行为。这些结果对研制纳米线磁子晶体器件具有参考意义。

关键词：磁子晶体；带隙；微磁学模拟；自旋波；圆柱形纳米线

0引言

磁子晶体是一种磁性、几何参数等性质在空间上周期性排列的人工磁性材料。由于磁子晶体的特殊性质，其在纳米器件和自旋波过滤器上存在各种应用[1-4]。类似声子晶体，自旋波在这类结构传播会形成一系列的通带和禁带[1,5-7]，我们可以通过改变周期参数来调制自旋波带隙结构。近些年来，人们设计和制备出了各种形式的磁子晶体。从维度的角度进行分类，有一维磁子晶体如周期性变化的多层膜[8-9]和周期调制的纳米带波导[10]，二维磁子晶体如有磁性纳米点的二维阵列结构[11-12]，还有一些三维磁子晶体结构[6,13]。通过对诸如外磁场[14]、磁参数[8-9,15]和磁体形状[16-19]的周期性调制可以形成不同结构的磁子晶体。

圆柱形纳米线及其阵列在磁信号传输、高密度存储等方面具有很多应用[20-21]。与制备过程繁琐的纳米带和多层膜相比，圆柱型纳米线和阵列可以利用操作简便的电化学沉积技术制备得到[22]。然而，据目前已有研究所知，圆柱型磁子晶体还没被研究过。在这篇文章中，利用微磁学模拟，我们对磁化强度周期变化的圆柱形纳米线磁子晶体作出了一系列的理论研究。结果显示，自旋波带隙结构能很好地通过磁子晶体磁化强度的变化和周期进行调制。

1方法和模拟参数

本文研究的圆柱形纳米线磁子晶体由磁化强度为M1和M2的两种铁磁性材料周期性交替组成，如图1(a)所示。纳米线长为3 020nm，直径30nm。磁子晶体的周期为P=P1+P2，其中P1、P2分别是M1和M2组分的长度。此外磁性参数的选择参考Fe1-xNix合金，通过改变组分含量，很容易调整Fe1-xNix合金的磁化强度。微磁学模拟时,取交换常数A1.3×10-11J/m,各向异性常数K=0,Gilbert阻尼系数α=0.01，M2为8×105A/m。为了研究磁化强度的调制对自旋波传播特性的影响，M1的取值从7×105A/m阶梯递减至3×105A/m。此外，我们还研究了不同周期长度P(P=60,80和100nm)的圆柱形纳米线磁子晶体。为简化起见，假设P1=P2。需要指出的是，这种磁子晶体可以基于多孔氧化铝模板采用电化学沉积的方法得到。通过调节沉积电压和沉积时间可以控制纳米线合金中Ni和Fe含量以及不同组分纳米线的长度[22]。

2结果与讨论

图1中给出了自旋波在P=60nm和M1=4×105A/m的纳米线磁子晶体中的传播特性图像。作为比较，自旋波在同几何尺寸的均质纳米线的传播图像也一并给出。从图1(b)看出，对于均质纳米线，存在一个截止频率约为12GHz，频率大于这一截止频率的自旋波均能在纳米线中传播。这一截止频率对应于波矢为零的铁磁共振频率。对于磁化强度调制的磁子晶体，自旋波表现出不一样的传播特性。与均质纳米线一样，磁子晶体同样存在一个截止频率，低于这一频率的自旋波不能传播，但在高于截止频率的频谱中也出现自旋波在某段频率内不能传播的清晰带隙，如图1(c)所示。沿着传播方向，自旋波强度还变现出明显的周期振荡，这一现象可以理解为自旋波在磁化强度周期变化边界发生了多重反射。自旋波的带隙结构还可以由图1(d)中自旋波强度在一个磁子晶体周期(2 000～2 060nm)内的平均值清晰地反映出来。图中可以看出，四条带隙位置(定义为带隙的中心频率)分别是18.02，32.09，51.87和73.68GHz，相应的带宽为3.91，2.98，9.37和1.09GHz。

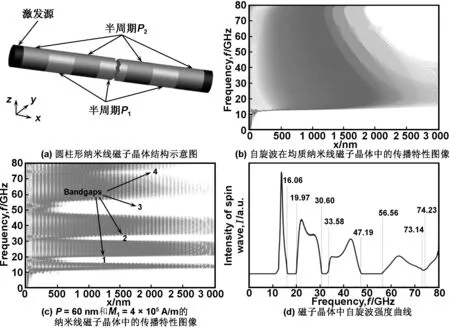
图1(a) 圆柱形纳米线磁子晶体结构示意图。左端暗红区域表示激发源。半周期P1为黄色区域，P2为淡红区域。自旋波在均质纳米线(b)及P=60nm和M1=4×105A/m的纳米线磁子晶体(c)中的传播特性图像(d)为磁子晶体中自旋波强度曲线。

Fig1 (a)Illustrationofmagnonic-crystalofcylindricalnanowoire.Spin-wavetransmissioncharacteristicsasafunctionofthepropagationdistancexforhomogenousmagnetizednanowire(b)andforamagnoniccrystalwithP=60nm, M1=4×105A/m(c), (d)Spin-waveintensityintegratedoveraperiodofMC(from2 000nmto2 060nm)

图2(a)和(b)分别给出了均质纳米线和磁化强度调制纳米线磁子晶体的色散关系。在均质纳米线中只有一条连续的抛物线型的色散关系曲线，对应于m=1的自旋波最低模式[24]。由于我们研究的纳米线直径很小(30nm)，自旋波传播的高阶模式没有激发出来。然而，纳米线磁子晶体的色散关系出现明显的带隙特征，见图2(b)。四条带隙所处位置恰好在布里渊(BZ)边界上(图2(b)中黑色虚线标明)，即k=nπ/P,n=2,3,4和5。这些带隙出现的原因是自旋波最低模式在周期结构中发生的Bragg反射。为了更加简单说明问题，我们标记带隙为Gn，n表示带隙所在BZ边界对应的指数。因此图2(b)中四条带隙分别对应为G2, G3, G4和G5。需要指出的是，G1带隙未在色散关系图像中反映出来的原因是其频率位置低于自旋波能在纳米线中传播的截止频率(12GHz)。

一般来说，带隙的位置和宽度主要取决于磁子晶体的周期和自旋波的色散关系。通常空间势变化率越大，带隙越宽。本文研究的磁子晶体周期势源自两磁化强度不同区域边界处的退磁场。因此通过调节磁化强度比值M1/M2，可以改变周期势和自旋波色散关系，从而达到调制自旋波带隙结构的目的。图3为M1=3×105A/m、P=60nm纳米线磁子晶体的自旋波传播图像及相应色散关系曲线。M1/M2比值的减小，所有带隙位置向高频方向移动，甚至带隙G5移出了我们所计算的频率范围。但是不同带隙的宽度变化不同，与前面的磁子晶体相比，带隙G2和G4变宽，带隙G3变窄。详细的模拟给出了自旋波带隙结构随比值M1/M2的变化规律。图4给出了磁子晶体周期P=60nm时，带隙位置fg(图4(a))和其宽度Δfg(图4(b))与磁化强度比值M1/M2的关系曲线。由曲线看出，带隙位置fg随着比值M1/M2的增加单调递减。

图2均质纳米线中和P=60nm, M1=4 × 105A/m纳米线磁子晶体中的自旋波色散关系曲线。黑色虚线对应布里渊边界

Fig2DispersioncurvesofspinwavespropagatinginhomogenousmagnetizednanowiresandinmagnoniccrystalwithP=60nmandM1=4 × 105A/m,theblackdottedlinesindicatethepositionoftheBrillouinzone(BZ)boundaries

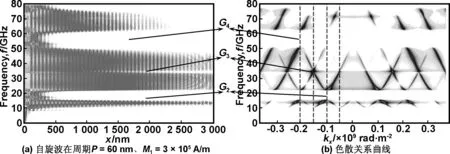
图3　自旋波在周期P=60nm、M1=3 × 105A/m的纳米线磁子晶体中传播时的频谱图和色散关系曲线

Fig3Spin-wavetransmissioncharacteristicsasafunctionofthepropagationdistancexanddispersioncurvesinamagnoniccrystalwithP=60nmandM1=3×105A/m

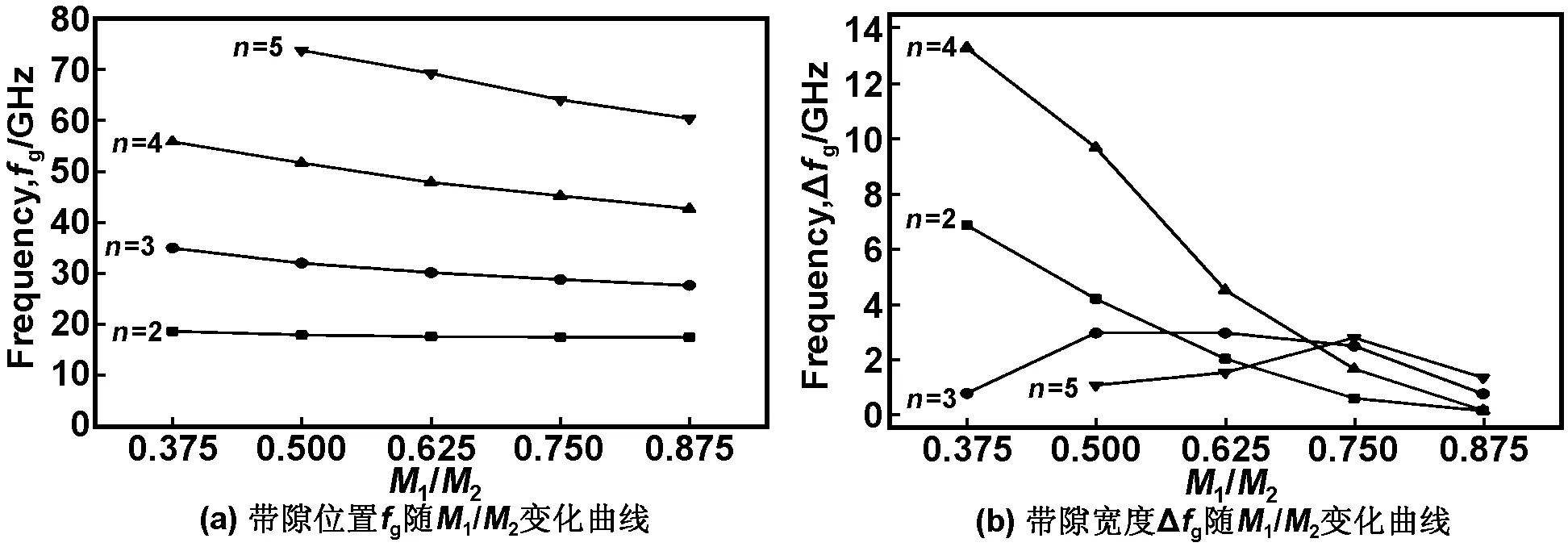
图4　磁子晶体周期为P=60nm时，带隙位置fg和带隙宽度Δfg随M1/M2变化曲线

Fig4DependenceofthebandgappositionfgandthebandgapwidthΔfgonM1/M2formagnoniccrystalwithP=60nm

然而带隙宽度Δfg与比值M1/M2的表现出更复杂的关系，总体上来看，随着比值M1/M2增加Δfg降低，但是某些带隙表现出宽度振荡的性质，如G3和G5带隙。如前所述，自旋波带隙取决于磁子晶体中的周期势(或周期性有效磁场)。对均质纳米线，除纳米线两端外，其内部有效场均匀且接近于零。对于磁化强度调制的磁子晶体，由于在两不同磁化强度组分界面处产生磁荷，导致有效场的增大，从而使自旋波色散曲线向高频移动。因此，尽管磁子晶体的周期没变(即布里渊边界没变)，然而带隙位置fg随着比值M1/M2的减小(有效场增大)而升高。此外，比值M1/M2的减小，还导致磁子晶体中有效场周期变化的增强，引起带隙宽度Δfg的增大。G3和G5这两个带隙随比值M1/M2的振荡变化可能与自旋波在界面处的透射/反射性质有关。一般而言，自旋波在界面处的透射率越大带隙越窄，透射率为1时，带隙消失。自旋波的透射率是频率的函数，且有时表现出振荡行为[25]。因此，带隙宽度Δfg的变化是由周期势场的空间变化和自旋波在界面处的透射性质所共同决定[26]。不同带隙所处频率位置不同，因此变化规律也不同，有的就会变现出振荡行为。

改变磁子晶体周期长度也是调制自旋波带隙结构的有效方法。为此我们研究了自旋波在不同周期纳米线磁子晶体中的传播性质。图5是比值M1/M2=0.5纳米线磁子晶体自旋波带隙位置fg和带隙宽度Δfg随周期长度P的关系关系。可以看出，周期的增大导致更多带隙的出现，P=60nm时只有4个带隙，P=80nm时有5个带隙，而P=100nm时出现了7个带隙。P的增大还引起带隙位置fg降低。带隙的这种变化可以用周期势一般能带理论来解释。周期的增大，导致布里渊边界波矢k=nπ/P的减小，从而引起带隙位置fg的降低。P的增大意味着倒格子空间周期的减小，因此在相同的频率范围内就会出现更多的带隙。从图5(b)看出，周期P的增大引起带隙宽度Δfg变窄。这是因为在M1/M2不变的情况下，周期越大意味着周期势空间变化的减缓，因此带隙变窄。

图5M1/M2=0.5时，带隙位置fg和带隙宽度Δfg随纳米线磁子晶体周期P的变化曲线

Fig5DependenceofthebandgappositionfgandthebandgapwidthΔfgontheMCperiodPwhenM1/M2=0.5

3结论

我们采用微磁学模拟的方法研究了自旋波在磁化强度周期变化的圆柱形纳米线磁子晶体中的传播特性。结果表明，自旋波在该类磁子晶体中传播会形成明显的通带和禁带(即带隙)，产生的原因是自旋波在布里渊边界发生Bragg反射。自旋波带隙结构可以通过磁子晶体的周期长度和磁化强度变化进行调制。随着磁化强度比值M1/M2的增加，磁子晶体内部有效场降低，从而使得带隙位置降低。带隙宽度随着比值M1/M2的增加而整体呈现出降低趋势，但某些带隙宽度出现较复杂的振荡性质。当磁子晶体周期长度增加时，带隙数目随之增加，带隙位置降低。带隙宽度由于受周期场的影响，随着周期长度的增加而减小。综上研究结果对制备基于纳米线磁子晶体的自旋波器件有着重要的参考价值。

参考文献:

[1]KimSK,LeeKS,HanDS.Agigahertz-rangespin-wavefiltercomposedofwidth-modulatednanostripmagnonic-crystalwaveguides[J].AppliedPhysicsLetters, 2009, 95(8): 082507.

[2]CarterRL,OwensJM,SmithJrCV,etal.Ion-implantedmagnetostaticwavereflectivearrayfilters[J].JournalofAppliedPhysics, 1982, 53(3): 2655-2657.

[3]SergaAA,ChumakAV,HillebrandsB.YIGmagnonics[J].JournalofPhysicsD:AppliedPhysics, 2010, 43(26): 264002.

[4]MaFS,LimHS,WangZK,etal.Micromagneticstudyofspinwavepropagationinbicomponentmagnoniccrystalwaveguides[J].AppliedPhysicsLetters, 2011, 98(15): 153107.

[5]WangZK,ZhangVL,LimHS,etal.Observationoffrequencybandgapsinaone-dimensionalnanostructuredmagnoniccrystal[J].AppliedPhysicsLetters, 2009, 94(8): 083112.

[6]KrawczykM,PuszkarskiH.Plane-wavetheoryofthree-dimensionalmagnoniccrystals[J].PhysicalReviewB, 2008, 77(5): 054437.

[7]TacchiS,MontoncelloF,MadamiM,etal.Banddiagramofspinwavesinatwo-dimensionalmagnoniccrystal[J].Physicalreviewletters, 2011, 107(12): 127204.

[8]DengDS,JinXF,TaoR.Magnonenergygapinaperiodicanisotropicmagneticsuperlattice[J].PhysicalReviewB, 2002, 66(10): 104435.

[9]NikitovSA,TailhadesP,TsaiCS.Spinwavesinperiodicmagneticstructures—magnoniccrystals[J].JournalofMagnetismandMagneticMaterials, 2001, 236(3): 320-330.

[10]DiK,LimHS,ZhangVL,etal.Tuningthebandstructuresofaone-dimensionalwidth-modulatedmagnoniccrystalbyatransversemagneticfield[J].JournalofAppliedPhysics, 2014, 115(5): 053904.

[11]ZivieriR,MontoncelloF,GiovanniniL,etal.Effectofinterdotseparationoncollectivemagnonicmodesinchainsofrectangulardots[J].Magnetics,IEEETransactionson, 2011, 47(6): 1563-1566.

[12]VasseurJO,DobrzynskiL,Djafari-RouhaniB,etal.Magnonbandstructureofperiodiccomposites[J].PhysicalReviewB, 1996, 54(2): 1043.

[13]TartakovskayaE,KreuzpaintnerW,SchreyerA.Spinwavedynamicsintwo-andthree-dimensionalsuperlatticesofnanosizedferromagneticspheres[J].JournalofAppliedPhysics, 2008, 103(2): 023913.

[14]BayerC,KostylevMP,HillebrandsB.Spin-waveeigenmodesofaninfinitethinfilmwithperiodicallymodulatedexchangebiasfield[J].Appliedphysicsletters, 2006, 88(11): 112504.

[15]CiubotaruF,ChumakAV,ObryB,etal.Magnonicbandgapsinwaveguideswithaperiodicvariationofthesaturationmagnetization[J].PhysicalReviewB, 2013, 88(13): 134406.

[16]LeeKS,HanDS,KimSK.Physicaloriginandgenericcontrolofmagnonicbandgapsofdipole-exchangespinwavesinwidth-modulatednanostripwaveguides[J].PhysicalReviewLetters, 2009, 102(12): 127202.

[17]SykesCG,AdamJD,CollinsJH.Magnetostaticwavepropagationinaperiodicstructure[J].AppliedPhysicsLetters, 1976, 29(6): 388-391.

[18]Al-WahshH,AkjoujA,Djafari-RouhaniB,etal.Largemagnonicbandgapsanddefectmodesinone-dimensionalcomblikestructures[J].PhysicalReviewB, 1999, 59(13): 8709.

[19]ChumakAV,SergaAA,HillebrandsB,etal.Scatteringofbackwardspinwavesinaone-dimensionalmagnoniccrystal[J].AppliedPhysicsLetters, 2008, 93(2): 022508.

[20]ChoiS,LeeKS,GuslienkoKY,etal.Strongradiationofspinwavesbycorereversalofamagneticvortexandtheirwavebehaviorsinmagneticnanowirewaveguides[J].PhysicalReviewLetters, 2007, 98(8): 087205.

[21]ParkinSSP,HayashiM,ThomasL.Magneticdomain-wallracetrackmemory[J].Science, 2008, 320(5873): 190-194.

[22]LiewHF,LowSC,LewWS.Fabricationofconstrictedcompositionally-modulatedNixFe1-xnanowires[C]//JournalofPhysics:ConferenceSeries,IOPPublishing, 2011, 266(1): 012058.

[23]DonahueM,PorterD.Theobjectorientedmicromagneticframework(OOMMF)projectatITL/NIST[J].URL:http://math.nist.gov/oommf, 1998.

[24]AriasR,MillsDL.Theoryofspinexcitationsandthemicrowaveresponseofcylindricalferromagneticnanowires[J].PhysicalReviewB, 2001, 63(13): 134439.

[25]WangX,GuoG,ZhangG,etal.AnanalyticalapproachtotheinteractionofapropagatingspinwaveandaBlochwall[J].AppliedPhysicsLetters, 2013, 102(13): 132401.

[26]WangX,GuoG,LiZ,etal.Spin-wavepropagationindomainwallmagnoniccrystal[J].EPL(EurophysicsLetters), 2015, 109(3): 37008.

Magnoniccrystalbasedonmagnetization-modulatedcylindricalnanowire

WANGMengning,LIZhixiong,TANGWei,NIEYaozhuang,GUOGuanghua

(SchoolofPhysicsandElectronics,CentralSouthUniversity,Changsha410083,China)

Abstract：Thecharacteristicsofspinwavespropagatinginmagnetization-modulatedcylindricalnanowirearestudiedbymicromagneticsimulations.Theallowedandforbiddenspin-wavebandsareobservedinthefrequencyspectraanddispersioncurves.TheyarecausedbytheBraggreflectionofthespinwavemodesattheBrillouinzoneboundaries.Thebandgapscanbeeffectivelycontrolledbymanipulatingtheperiodofmagnoniccrystalorthemagnetizationratio.Theresultsshowthatthenumberofbandgapsincreaseswiththeincreaseoftheperiod,thebandgapsshifttolowerfrequencyandthebandgapwidthsdecrease.Theenhancementofthemagnetizationmodulationalsodisplacesbandgappositiontowardthelowfrequency.Whilethevariationofthebandgapwidthsdisplayscomplicatedformandsomebandgapsexhibitoscillationcharacteristic.Theresultspresentedheremayfindtheiruseindesigningmagnonicdevices.

Keyword:magnoniccrystal;bandgaps;micromagneticsimulations;spinwave;cylindricalnanowire

文章编号：1001-9731(2016)06-06076-05

* 基金项目：国家自然科学基金资助项目(11374373)；教育部博士点基金资助项目(20120162110020)；湖南省自然科学基金资助项目(13JJ2004)

作者简介：(1991-)，女，江西上饶人，硕士，师承聂耀庄教授，从事磁性材料研究。

中图分类号：O441.2

文献标识码：A

DOI:10.3969/j.issn.1001-9731.2016.06.013

收到初稿日期：2015-05-08 收到修改稿日期：2015-07-23 通讯作者：郭光华，E-mail:guogh@mail.csu.edu.cn