基于Cauchy主值积分的高振荡函数的数值计算

周勇攀

(武汉工程大学计算机科学与工程学院，湖北 武汉 430074)



基于Cauchy主值积分的高振荡函数的数值计算

周勇攀

(武汉工程大学计算机科学与工程学院，湖北 武汉 430074)

摘要：含高振荡函数的Cauchy主值积分dx,-1<τ<1，基于解析延拓定理，用最速下降法将其转化成在[0,+∞)上非振荡且指数快速下降的积分，再利用Gauss-Laguerre求积法则高效逼近计算，最后用两个数值实例来说明该方法的合理性.

关键词：Cauchy主值积分；最速下降法；Gauss-Laguerre求积法则

0引言

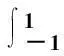
我们讨论含高振荡函数的Cauchy主值积分

(1.1)

其中，f在包含[-1,1]的一个充分大的复区域内解析，如果f在[-1,1]上满足霍尔德条件[4]，我们知道这个积分存在[5].对式(1.1)，用一个半圆包含奇异点τ的邻域(图1)，结合复积分方法和最速下降法得到4个在[0,+∞)上非振荡且指数快速下降的积分，再用Gauss-Laguerre求积法则高效逼近计算[6-7].

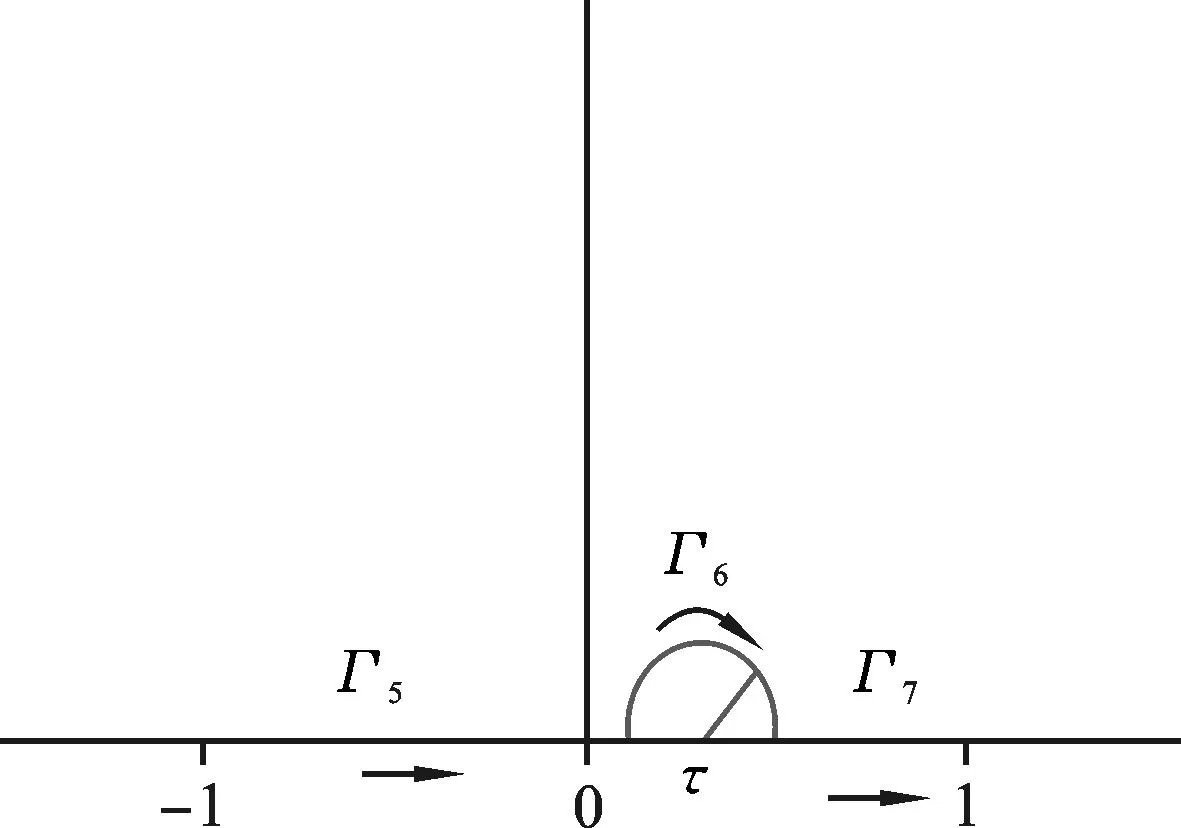
图1　原给异点τ的邻

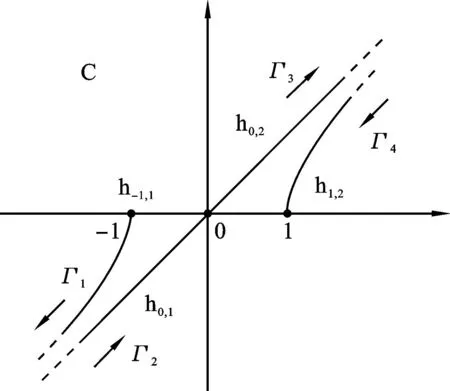
图2　最速下降路径

1计算结果

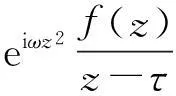
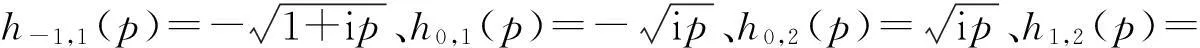
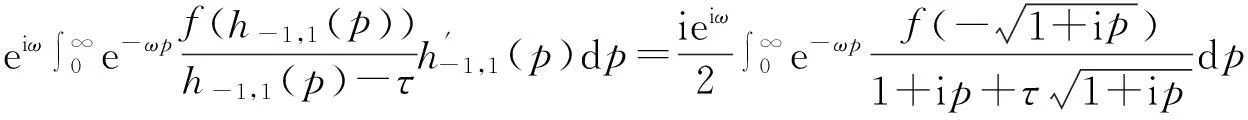
同理，

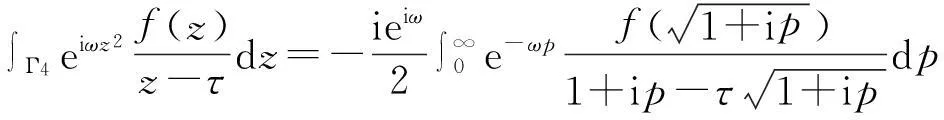
由于路径Γ6是一个围住z=τ的半圆，即z-τ=reiθ,0≤θ≤π,则

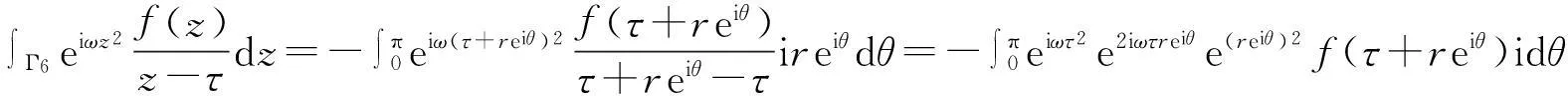
当r→0时，|z-τ|→0，f(z)在点τ处是连续的，即|f(z)-f(τ)|→0,

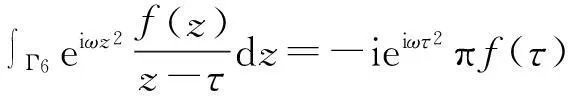
此时，再由定义的主值积分和式(1.2)，得到

(1.3)

其中，t=ωp.

计算得到的积分我们就可以用Gauss-Laguerre求积法则来估计，含振荡函数的Cauchy主值积分估计得到

(1.4)

其中，xk和wk分别为n阶Gauss-Laguerre公式的节点和权.

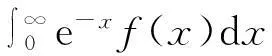
其中,ξ1、ξ2、ξ3、ξ4∈C，当ω≫1，误差的渐近估计为O(ω-2n-1)，因此计算的误差精度随着ω的增加而快速提高.

定理1假设f和g在一个包含区间[-1,1]的充分大的复区域D内解析，并且g的反函数在D内存在，如果下面的条件在D内满足：

∃m∈N∶|f(z)|=O(|z|m),∃ω0∈R∶|g-1(z)|=O(eω0|z|),|z|→∞,

即对于x∈[-1,1]，存在一个函数F(x)，使得F(x)=∫Γxf(z)eiωg(z)dz，其中Γx是一个起始于x的一个路径，hx(p)是Γx的一个参数化表示，p∈[0,∞)，误差E=F(x)-QF[f,g,hx]的渐近估计为O(ω-2n-1)，其中QF[f,g,hx]是由n阶Gauss-Laguerre求积法则得到的[2].

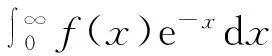
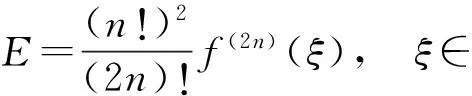
再用这个公式，我们能导出误差的一个表达式E=F(x)-QF[f,g,hx];

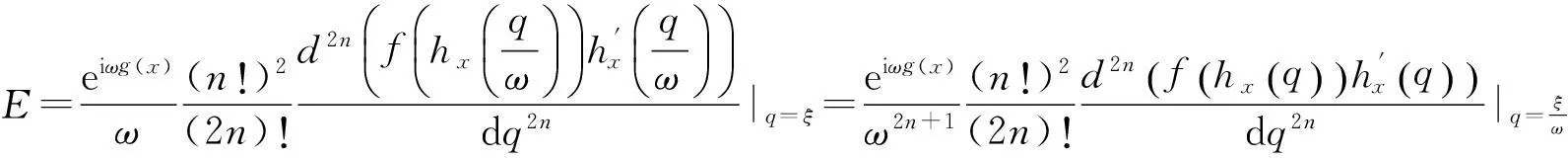
其中，ξ∈C，误差的渐近估计为O(ω-2n-1)得证.

2数值实例

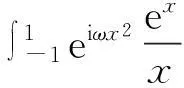
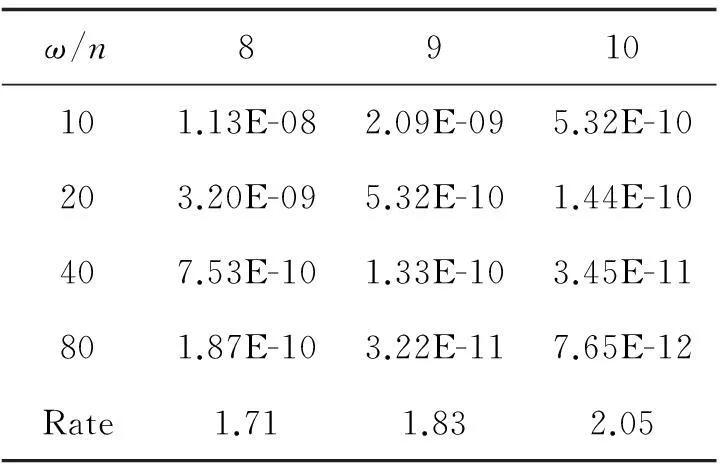
表1　Filon方法计算的绝对误差

可以看出，用Filon方法计算积分，对于固定的频率ω，逼近的精度随插值节点数目n的增加而提高，并且频率越大，精度提高的越快.

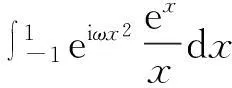
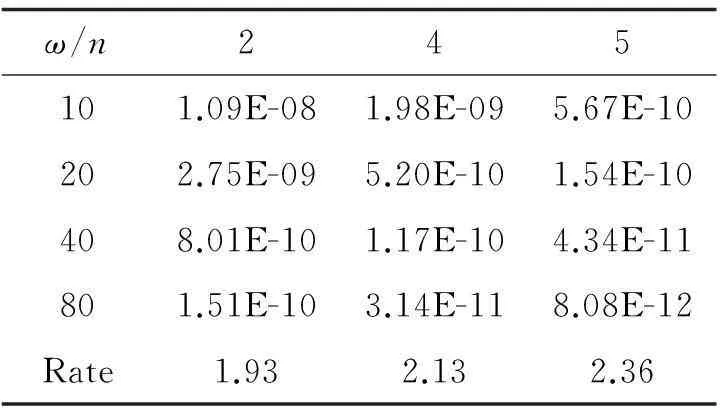
表2　利用n点Gauss-Laguerre积分法

计算的绝对误差.

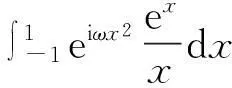
从表2可以看出，对于含Cauchy核的高振荡的数值积分，用数值最速下降法来计算，我们也得到同样的结论，即对于固定的频率ω，逼近的精度随Gauss-Laguerre节点数目n的增加而提高，并且频率越大，精度提高的越快；另外与表1对比，我们只需要取较少的节点，就可以得到相同的误差精度.

3参考文献

[1] Milovanovic G V.Numerical calculation of integrals involving oscillatory and singular Kernels and some applications of quadratures[J].Comput Math Appl,1998,36(8):19-39.

[2] Huybrechs D,Vandewalle S.On the evaluation of highly oscillatory integrals by analytic continuation[J].SIAM J Numer Anal,2006,44(3):1026-1048.

[3] Wang Haiyong ,Xiang Shuhuang.On the evaluation of Cauchy principal value integrals of osc-illatory functions[J].Comput Math Appl,2010,234:95-100.

[4] 路见可.解析函数边值问题[M].2版.武汉：武汉大学出版社,2004.

[5] Davis P J ,Rabinowitz P.Methods of Numerical Integration[M].second edition.New York:Acade-mic Press 1984.

[6] Ablowitz M J,Fokas A S.Complex variables:introduction and applications[M].Cambridge,UK:Cambridge University Press,1997.

[7] Wong R.Asymptotic approximation of integrals[M].Philadelphia :SIAM,2001.

[8] Abramowitz M,Sterun I A.Handbook of Mathematical Functions[M].Washington DC:National Bureau of Standard,1964.

[9] Huybrechs D,Olver S.Highly oscillatory quadrature//Engquist B,Fokas T,Hairer E,A.Iserles Highly Oscillatory Problems[M].Cambridge,UK:Cambridge University Press,2009:25-50.

(责任编辑赵燕)

Value integrals of highly oscillatory functions based on the evaluation of Cauchy principal

ZHOU Yongpan

(School of Computer Science and Engineering,Wuhan Institute of Technology,Wuhan 430074,China)

Abstract:The problem of numerical evaluation of Cauchy principal value integrals of highly oscillatory functions dx,-1<τ<1，had been discussed.Based on analytic continuation and the steepest descent method ,the integrals can be transformed into the problem of integrating on[0,+∞) with the integrand that does not oscillate,and that decays exponentially fast,which can be efficiently computed by using the Gauss-Laguerre rule.The validity of the method has been demonstrated in the provision of two numerical experiments and their results.

Key words:Cauchy principal valueintegrals;steepest descent method;Gauss-Laguerre rule

中图分类号:O241.38；O174.41

文献标志码:A

DOI:10.3969/j.issn.1000-2375.2016.03.017

文章编号:1000-2375(2016)03-0267-04

作者简介：周勇攀(1990-)，男，硕士生

收稿日期:2015-09-15