《圆柱与圆锥》素养进阶习题设计

文|黄招杰

一、素养专项展评

1.柱体体积的联系（巧用知识关）

（1）计算下面图形的体积。（单位cm）

（2）这几个图形在体积的计算方法上有什么相同点？

（3）猜测：下面哪些图形的体积也可以运用这种方法来计算。（）（填序号）

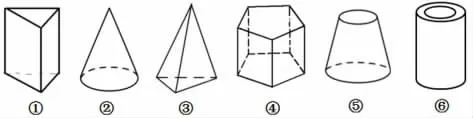
（4）你选中的图形和题目中的三个图形，从图形的运动角度观察，都可以经平面图形的（ ）（填平移或旋转）得到。

【参考答案】

（1）20×10×15=3000（cm3）

10×10×10=1000（cm3）

3.14×42×12=602.88（cm3）

（2）底面积×高

（3）①④⑥

（4）平移

【设计意图：通过柱体体积的计算，寻找体积计算的共性，根据立体图形特征的整体把握，迁移共性，达到图形特征与度量的整体融合。本题考查空间观念和几何直观。】

2.从生活走向数学（问题解决关）

（1）李伯伯既是一位木匠，又是一位书匠。这是他锯下的一个木桩，他利用这个木桩给他的学生提了一些问题，如下图所示。你知道每个问题求的是什么吗？请在（）内填上正确的序号。

①给这个木桩打一道铁箍，需要多长的铁丝？（ ）

②把这个木桩放倒，在地上滚一周，所形成的面积是多少？（ ）

③把木桩放在地上，它的占地面积是多少？（ ）

④在木桩外面涂油漆，油漆面的大小是多少？（ ）

⑤计算这个木桩所占空间的大小？（ ）

A.底面积 B.底面周长

C.侧面积 D.表面积

E.侧面积+底面积 F.体积

（2）你可以用什么方法把这个圆柱体木桩变成另外的物体呢？老师这里提供了几种方法，请你任选一种，自编一道能用以上数据就可以解决的数学问题。

A.锯一锯 B.挖一挖

C.削一削

我选（ ）：问题：我选（ ）：问题：

（3）李伯伯计划将这个木桩改造成一个木桶，如图所示。现要知道这个木桶最多能装多少的水，需要测量哪些数据？我的选择是（）。（填序号）

A.外直径

B.内直径

C.桶口距底面最小高度

D.桶口距底面最大高度

【参考答案】

（1）B、C、A、D、F

（2）略（开放式题目，比如①沿着直径，往下锯，表面积多了多少？②挖一个直径为10cm 的最大的圆柱，剩下的体积是多少？③削成一个最大的圆锥，圆锥体积是多少？）

（3）BC

【设计意图：利用生活中的问题，丰富学生的“实践经验”。第（2）题的开放设计让不同的学生达到不同的高度。培养学生分析问题、寻找信息的能力。本题考查应用意识和创新意识。】

二、素养综合展现

3.用数学的思维想问题（探索奥秘关）

在这个单元学完后，小明和小佳两人就一个问题展开了研究，题目是这样的：下面四个图形的面积都是36。分别以长和宽为轴旋转一周，各得到两个圆柱体。哪个圆柱的体积最小？哪个圆柱的体积最大？你有什么发现？

（1）先从简单开始，研究一个图形。

绕长旋转：长方形的长是圆柱的（），宽是圆柱的（）。

绕宽旋转：长方形的长是圆柱的（），宽是圆柱的（）。

（2）计算体积。

小明是这样算的：

绕长旋转：

V=sh=3.14×22×18=226.06

绕宽旋转：

V=sh=3.14×182×2=2034.72

小佳是这样算的：

绕长旋转：

V=sh=3.14×2×2×18

绕宽旋转：

V=sh=3.14×18×18×2

小明说：“你没有算出得数，不能比较体积的大小。”

小佳说：“我从算式中就可以看出来哪个大、哪个小，不用计算出结果。”

你同意谁的说法？能说说你的理由吗？

（3）要根据不同的情况选择不同的策略来解决问题。

现在我们的研究结论是：绕宽旋转的圆柱体积（ ）绕长旋转的圆柱体积。然后我们还发现在比体积哪个大、哪个小的时候，就是在比两个圆柱的（ ），（ ）越长，体积越大。

（4）猜测：①号图形的结论可以应用到②号、③号吗？能说说你的想法吗？

（5）结论：我们会发现每个图形都是绕（ ）旋转的时候，圆柱体积比较大。在这四个圆柱里面，哪个体积是最大的呢？

猜测：（ ）越长，体积越大。

（6）验证：小明也这样进行比较：请你在算式中，将决定体积大小的数圈出来。

V1=18×18×2×π

V2=12×12×3×π

V3=9×9×4×π

V4=6×6×6×π

（7）结论：我发现了：（ ）号长方形绕（ ）旋转体积最大。同样可以类推：（ ）号长方形绕（ ）旋转体积最小。注意：结论的成立，前提是长方形的面积都得相同。当我们要研究一个比较复杂的问题时，通常需要从简单的问题入手，经历猜测、验证、再猜测、再验证的过程。

【参考答案】

（1）高，半径；半径，高

（2）同意小佳：都有3.14×2×18，18＞12，所以绕宽旋转体积大。

（3）＞，半径，半径

（4）可以

（5）宽，半径

（7）①宽；①长

【设计意图：学会将复杂问题化成若干个简单问题，经历猜测、验证、再猜测、再验证的反复过程，注重合情推理和演绎推理的融合，掌握数学研究的一般方法，得到正确的结论。本题考查空间观念、推理意识和创新意识。】