再生冷却结构非定常换热计算研究

张若凌，张磊，王想义，蒋劲，顾磊

中国空气动力研究与发展中心 高超声速冲压发动机技术重点实验室，绵阳 621000

0 引 言

碳氢燃料超燃冲压发动机工作时，燃气温度很高，即使采用复合材料也无法承受燃烧室内巨大的热载荷。在发动机中，一般采用燃油再生冷却方法解决热防护问题[1-3]。采用燃油再生冷却既可以利用燃料的吸热性质降低发动机壁面温度，又可以减小系统重量。受燃料热沉能力限制和积碳影响，目前国际上普遍认为在飞行马赫数低于8 时可采用碳氢燃料[4-6]进行再生冷却。

中国空气动力研究与发展中心（CARDC）从2003年开始进行超燃冲压发动机再生冷却传热的计算和试验研究，基于国内某航空煤油的组分测量建立了冷却剂的物性模型，结合大规模并行CFD 流场计算工具AHL3D[7-9]，建立了定常换热分析工具和初步的冷却通道设计方法，进行了冷却剂分别为水和航空煤油的发动机试验研究[10-13]。

目前针对超燃冲压发动机再生冷却结构非定常换热的研究未见报道。进行非定常换热分析，可以获得发动机的热平衡特性，对发动机再生冷却结构设计和试验研究十分重要，可为热结构风洞建设提供依据。

本文首先建立发动机再生冷却结构的非定常换热计算模型；然后，通过对比发动机（冷却剂分别为水和航空煤油）计算与试验数据，验证非定常换热计算模型，分析非正规阶段温升时间；最后，计算分析发动机初始壁面温度对达到热平衡时间的影响。

1 非定常换热计算模型

在壁面温度趋近于平衡值的过程中，存在2 个阶段：在第一阶段里，温度分布主要受初始温度分布影响，即非正规阶段；在第二阶段里，不同时刻的温度分布主要取决于边界条件和物性，即正规阶段[14]。若超燃冲压发动机的壁面较薄，则非正规阶段温升的时间远小于达到热平衡的时间，下文的分析基于发动机壁面的温度分布处于正规阶段的假设。

发动机壁面由图1 所示的再生冷却面板组成。假设发动机固壁内在沿着冷却剂流动的方向上没有传热。一个通道在流向某位置上的截面如图2 所示（y 轴沿冷却通道的高度方向），燃气垂直纸面向内流动，冷却剂垂直纸面向外流动，冷却通道宽Lc、高Hc，肋片厚度D，一个冷却通道的宽度为Lc+D，衬层厚度b1，涂层（TBC）厚度b2。

图1 再生冷却面板Fig. 1 Regenerative cooling panel

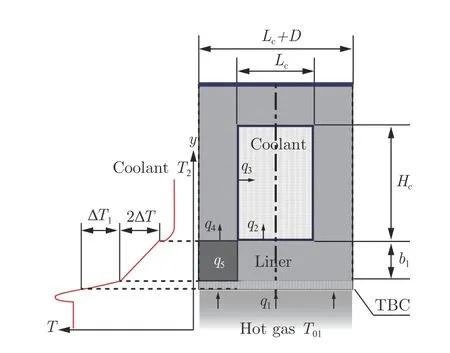
图2 再生冷却通道截面Fig. 2 Regenerative channel section

燃气侧壁面热流密度q1和衬层冷却剂侧热流密度q2的计算公式[12]如下：

式中：h1为燃气与壁面的换热系数，T01为燃气恢复总温，T 为衬层的平均温度，∆T 为衬层两侧温差的一半，∆T1为涂层两侧温差，h2为冷却剂与衬层壁面的换热系数，T2为冷却剂的平均温度。

发动机壁面选用不锈钢或高温合金材料，其导热系数比冷却剂大很多，热量经冷却通道四周传向冷却剂。燃气侧壁面热流密度q1可以分为4 部分：一部分热流密度使冷却剂正下方的衬层和涂层升温，一部分热流密度q2通过衬层传向冷却剂，一部分热流密度q4传给肋基，还有一部分热流密度q5使肋基正下方的衬层和涂层升温。假设冷却面板外侧绝热，把肋片上端半宽为Lc/2 的外侧金属层部分也看作厚度为D/2 的肋片，则整个肋片的高度为Hc+Lc/2。

假设整个衬层的温度分布相同，通过肋基的热流密度q4可以分成2 部分：一部分使整个肋片升温，一部分是通过肋片传向冷却剂的热流密度q3。q3计算公式如下：

式中：h3为肋片与冷却剂的平均换热系数，Tfin为肋片平均温度。

由于金属的热阻远小于流体，肋基处热流密度比冷却剂侧热流密度大，即q4>q2。当发动机壁面温度达到平衡分布时，肋基处热流密度可以通过肋片效率η定义：

式中：k1为衬层热导率，下标“eq”表示平衡状态。

为计算非定常阶段的温升，令每一时刻使衬层、涂层升温和通过衬层传向冷却剂的总热流密度为φq1（φ为热流比例系数），并假设在每一时刻均满足：

由式（6）、（7）可推导出：

衬层和肋片升温过程的控制方程分别为：

式中：ρ1、c1分别为衬层的密度和比热；ρ2、c2分别为涂层的密度和比热，t 为时间。由图2、式（10）、（11）可知，单位时间的温升等于流入的热流密度与流出的热流密度之差除以单位面积单位时间温升所需的热量。式（10）可用来确定q5，同时根据式（9）和（10）可以确定q4。式（11）可以改写为：

考察衬层处情形，认为在每一时刻衬层和涂层的温度分布处于正规阶段，假设：

式中：k2为涂层热导率。将式（1）、（2）代入式（13），得到：

将式（1）、（2）、（8）代入式（10），并用式（14）替换∆T、∆T1，得到：

其中，C 和λ表达式分别为：

式（15）就是衬层温升过程的控制方程，初值条件为衬层平均温度T(t = 0) =T0。若近似认为物性和换热系数为常数，其解为：

式中：Teq为平衡温度， （Teq−T0）e−λt表征非定常过程，即衬层温度向平衡温度趋近的过程。需要指出的是，h1随燃气和壁面温度变化不大，h2随冷却剂温度变化较大。

定义衬层非定常温升时间τ为衬层平均温度达到0.99 倍平衡温度的时间，则：

可以看出，τ除了与材料物性、结构和冷却剂的换热性质相关外，还与衬层初始温度T0相关，T0与Teq越接近（相对差别须大于1%），τ越小。

肋片处的温升过程根据式（12）求解，本文不做进一步推导。在计算中冷却剂流动采用一维方法处理，沿着流动方向步进，就可以得到沿冷却通道壁面的温度分布。换热系数h1采用Eckert 参考焓方法[15]计算，考虑进口效应的换热系数h2采用修正Bartz方程[16-17]计算。

2 非定常换热计算模型验证

2.1 发动机热平衡时间分析

CARDC 于2004—2005 年在电弧加热器设备（图3）上开展了水冷却和航空煤油冷却直连式超燃冲压发动机（无燃烧）换热试验。发动机采用不锈钢材料（1Cr18Ni9Ti）制成，燃气侧壁面没有涂层。发动机气体内流道入口高32 mm、宽100 mm，冷却通道宽3 mm、高3 mm，肋片宽3 mm，衬层厚3 mm。设备来流总温1100 K，来流总压1.6 MPa，空气质量流量3.2 kg/s，燃烧室入口马赫数为2，冷却剂入口温度297 K、压力7 MPa。

图3 再生冷却发动机测试设备Fig. 3 Regeneratively cooled scramjet test facility

图4 和5 分别是水冷却和航空煤油冷却试验条件下的典型外壁温度历程曲线。可以看出，水冷却试验中模型的外壁温度基本达到了稳定状态，非定常温升时间约23 s；航空煤油冷却试验中模型的外壁温度未能达到稳态分布，有效试验时间约28.5 s。

图4 水冷却试验中外壁温度历程Fig. 4 Histories of the outer wall temperature in water cooling test

图5 航空煤油冷却试验中外壁温度历程Fig. 5 Histories of the outer wall temperature in kerosene cooling test

采用非定常换热计算模型，在相同工况下，对试验中的超燃冲压发动机结构开展水冷和航空煤油冷却换热特性计算。单条冷却通道的水和航空煤油质量流量分别为3.5 和3.0 g/s。计算得到一条冷却通道的冷却剂侧壁面不同点的温升曲线分别如图6和7 所示。由图可知，水冷时发动机结构达到热平衡的时间约为20 s，航空煤油冷却时达到热平衡的时间约为45 s。

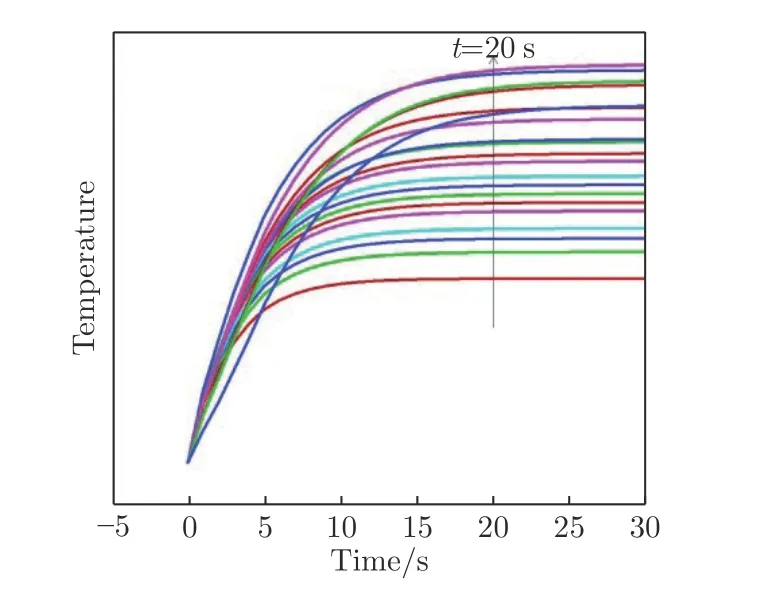
图6 水冷却试验条件下壁温计算Fig. 6 Calculated wall temperature under water cooling condition

图7 航空煤油冷却试验条件下壁温计算Fig. 7 Calculated wall temperature under kerosene cooling condition

需要指出的是，在图4、6 和7 中，确定模型外壁温度基本达到稳态的时间的方法具有一定的主观性。更加严谨的方法要求给出温度达到稳态的一致性判据，例如在稳态温度未知时，采用温度对时间导数为该导数最大值的5%或10%所需的时间，或者在稳态温度值已知时采用温度达到0.99 倍平衡温度的时间。本文意在说明相同的试验参数下，航空煤油冷却试验中模型外壁温度基本达到稳态的时间明显比水冷却试验更长，因此本文采用的方法也是可行的。

从式（16）、（17）和（19）可以看出，采用不同冷却剂得到发动机达到热平衡的时间差别较大，主要原因是冷却剂换热系数不同。在所讨论的条件下，水的换热系数比航空煤油大，即水的冷却性能比航空煤油好，使发动机达到热平衡的时间更短。

对比图4 和6 可知，在水冷条件下，计算和试验得到的发动机达到热平衡时间差别约为3 s（在计算中假定肋片效率η在温升过程中保持不变并忽略相邻单元沿冷却剂流向的传热，这些是产生误差的因素），二者吻合较好，对本文建立的再生冷却结构非定常换热计算模型进行了初步验证。

2.2 非正规阶段温升时间分析

研究非正规阶段温升时间时，可采用平板模型近似替代带冷却通道的燃烧室壁板。该阶段冷却剂吸热较少，简化计算中可不考虑。一侧加热、一侧绝热的平板温度分布的精确解为[14]：

式中：Tp0为平板初始温度，qp为加热的热流密度，ρp、cp、bp、kp分别为平板的密度、比热、厚度和热传导系数，热扩散系数α=kp/(ρpcp)，x = 0 为绝热侧壁面位置，x=bp为给定热流密度侧壁面位置。

式（20）右端第四项表征非正规阶段的温度分布，随着时间增长呈指数衰减，当（即傅立叶数Fo）较大时，可忽略此项。选取3.1 节不锈钢材料的物性参数，取ρp=8000 kg/m3、kp= 16 W/(m·K)（300 K 对应的数据）、bp= 3 mm、cp= 500 J/(K·kg)。当指数为–3 时（e–3= 5.0%），Fo = 0.304，非正规阶段的温升时间为0.68 s。

由图4 和5 可知，水冷却发动机非正规阶段温升时间约为2.5 s，航空煤油冷却时该时间约为1 s，比式（20）计算得到的时间长。这是因为式（20）适用于一侧绝热平板，实际上再生冷却超燃冲压发动机的壁板不能简单假设为平板，且冷却剂还要从衬层吸热。由于温度较低时航空煤油的换热系数比水小，因此航空煤油冷却发动机非正规阶段温升时间较短。

2.3 壁面预加热对热平衡影响分析

在建设超燃冲压发动机热结构风洞时，需要掌握发动机达到热平衡的时间，采用传热性能良好的材料和通道构型可以缩短达到热平衡时间。由式（19）可知，在发动机试车前对发动机壁面进行预加热处理（即提高T0初始值），可缩短发动机达到热平衡的时间，从而节约热结构风洞的运行时间。

采用本文的非定常换热计算模型，计算发动机一条冷却通道壁面初始温度分别为300 和800 K 时的非定常阶段温升过程，得到不同时刻冷却剂侧壁面沿程温度分布如图8 和9 所示。

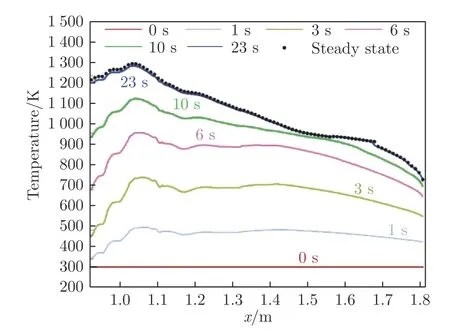
图8 初始温度300 K 时壁面温度沿通道方向的分布Fig. 8 Distributions of wall temperature along tube under initial wall temperature 300 K

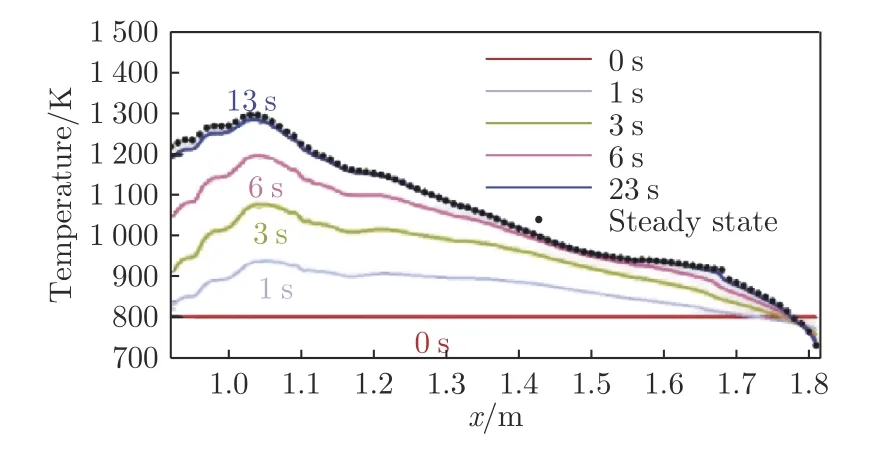
图9 初始温度800 K 时壁面温度沿通道方向的分布Fig. 9 Distributions of wall temperature along tube under initial wall temperature 800 K

计算采用的发动机壁面材料为不锈钢（1Cr18Ni9Ti），燃气侧壁面有0.1 mm 的ZrO2涂层。来流条件对应飞行马赫数6，发动机冷却和燃烧油气比均为1.1（燃气总温最高约2700 K）。冷却剂为航空煤油，入口压力7 MPa，从发动机出口向入口方向流动，每根通道流量1 g/s。由图8 和9 可知，初始壁面温度分别为300 和800 K 时，发动机达到热平衡时间分别约为23 和13 s。由此可知，对发动机壁面进行预加热可以缩短达到热平衡的时间。需要指出的是，此处计算得到的达到热平衡的时间，未考虑冷却剂流量的影响。

进行非定常阶段温升时间的初步估算对于一些实际应用意义重大。在包含冷却流动的传热试验中，传热过程是十分复杂的。壁温升高特性主要取决于：1）固体的传热过程，非常接近线性；2）在冷却通道里的流动中，存在复杂的非线性特征，即冷却剂物性参数发生很大变化以及实际的对流边界层存在非线性特征；3）燃烧室热流密度分布的不均匀特性，主要是总温和激波等干扰带来的加热条件分布不均。

若要采用某个简单公式来进行非定常阶段温升时间的初步估算，必须采用一些简单假设。通过反复验算发现，对于典型的再生冷却超燃冲压发动机而言，冷却剂物性取300 K 对应的数据，燃气恢复温度取1650 K（对应飞行马赫数6 ），换热系数和壁面物性取壁温900 K 对应的数据，利用式（19）进行非定常阶段温升时间初步估算是合适的。以图8 和9 研究的再生冷却超燃冲压发动机结构（1/λ=5.34 s，C/λ=892.2 K）为例：当初始壁面温度300 K时，得到非定常阶段温升时间22.39 s，与图8 结果一致；初始壁面温度800 K 时得到非定常阶段温升时间12.46 s，与图9 结果一致。

3 结 论

本文建立了超燃冲压发动机再生冷却结构的一种非定常换热计算模型，进行了发动机换热特性分析，得到以下结论：

1）在所讨论的水冷却条件下，计算和试验得到的发动机达到热平衡时间分别为23 s 和20 s，二者较为吻合，初步验证了本文建立的非定常换热计算模型。

2）给出了一种发动机非正规阶段温升时间的计算方法，且温升时间的计算与测量结果吻合较好。

3）计算结果表明，试验前对发动机壁面进行预加热可以缩短发动机达到热平衡的时间，从而节约热结构风洞的运行时间。

4）本文建立的再生冷却结构非定常换热计算模型具有一定的适用性，能够应用于超燃冲压发动机的传热特性分析。