基于单元教学的高中数学学业评价研究
高波 孙元勋



【摘要】在核心素养评价框架下,采用以单元测评为主的纸笔评价方式,测评过程包括设计双向多维细目表、精准命题、测验、收集测评数据、测评结果反馈。对单元学习情况进行评价目的是了解学生对单元核心知识的掌握情况,反映学生单元学习质量,同时为教师教学提升与改进提供依据。
【关键词】高中数学;学业评价;单元测评
学生的学业评价一直以来都是教育教学领域中的一个重点问题。《普通高中数学课程标准(2017年版2020年修订)》对高中数学学业质量提出了明确的要求:数学学科学业质量是应该达成数学学科核心素养的目标,是数学学科核心素养水平与课程内容的有机结合。学业质量是学生自主学习与评价、教师教学活动与评价、教材编写的指导性要求,也是相应考试命题的依据。
核心素养的提升显然已成为数学教育的主要目标,是数学教学的重要任务,而大单元教学被视为落实核心素养的一条有效的教学路径。因此在教学实践中,为了检验核心素养的落实效果,还需要在单元整体性教学后,结合课标中对学业质量评价的要求与建议进行有效的单元测评。这种单元测评包括了试题的命制、纸笔测验、测评的数据分析与结果反馈等过程,体现了教、学、评的一体化,对高中数学教学改进具有一定的导向作用。
一、单元测评的方式与目的
单元测评是以学生为评价对象,以单元知识为评价目标,测量学生个体对单元知识学习情况的一种过程性评价。测评数据有利于反映学生数学学科核心素养提升发展的过程。
单元测评的目的体现在以下三个方面:
1.学生学习动力的提升
单元测评目的体现了以人为本的思想,让学生在激励性评价中体验学习的快乐,从而提高学生学习的兴趣,持续地激发学生内驱式的学习动力。
2.多维评价的自我成长
单元测评应既包含对学生已掌握知识的能力水平的评价,也应包含对学生学习方式、态度、习惯和学习潜力的评价。避免评价的单一,注重在过程中使用多维评价方式,促进学生自我成长。
3.教师教学的改进
单元测评考查学生对本单元学习的成效,也考查教师教学的成效。通過单元测评,既能帮助教师了解学生的学习情况,也能反馈教学效果。通过结果诊断,不但能改进学生的学习行为,而且还能促进教师教学行为的改进,从而实现教师对自身数学教学经验的不断反思和超越。
二、单元测评的命题设计
《普通高中数学课程标准》对高中数学学业质量的内涵、学业质量水平与考试评价的关系作了明确的说明,对教学学业水平考试与命题提出实施建议。依据《普通高中数学课程标准》的建议进行单元测评命题,才能使单元测评的命题设计与课标要求保持一致。
1.单元测评命题“度”的把握
(1)试题难度的把握—精准把握、难度适中。单元测评的试题难度要做到精准把控,命题应依据学业评价标准以单元基础知识为主,从学生实际出发,降低起点、控制难度,提高效度,满足不同层次的学生,使大部分学生容易着手。
(2)考试时间与题量的把握—整体优化、合理设值。关注试卷的整体性,处理好考试时间和题量的关系,合理设置题量与相应的分值,关注考查的内容在题型与难度上的分布。下面给出两个设计方案供参考:
方案1:测评时间90分钟。试卷整体结构包括单选题4道、多选题4道、填空题4道、解答题4道。分值设置为单选、多选、填空题每题各5分,解答题每题10分,总分值100分。三级水平的分值比例为6:3:1。
方案2:测评时间90分钟。试卷整体结构包括单选题8道、多选题4道、填空题5道、解答题4道。分值设置为单选题每题4分、多选题每题5分、填空题每题4分,解答题每题12分,总分值120分。三级水平的分值比例为7:2:1。
2.命制试题的原则与路径
命制试题的原则:明确核心知识的评价要求,以学业要求的达成为目标,以核心知识为基础、以问题情境为载体,以思想方法为依托,以关键能力为特征,综合体现数学核心素养的落实。命题的路径是先设计双向细目表,再编制测试题。
三、单元测评多维度的数据分析
高中数学课程标准中明确了数学学科核心素养(即六种关键能力)及三个水平的划分依据,这六种数学关键能力相互交织。因此检测的题目可能一道题考查几种关键能力,也可以考查几种数学能力和考量不同的水平。下面以“数列”单元测评为案例来具体说明。
案例:“数列”单元测评。
1.测评的基本情况概述
(1)命题人:高波。
(2)测评时间:2021年12月28日16:30-18:00。
(3)测评人员:海口市第一中学高二年级全体学生。
(4)有效试卷:1227份。
(5)试卷整体结构:单选题4道,多选题4道,填空题4道,解答题4道,分值分配为单选、多选、填空题每题各5分,解答题每题各10分,总分值100分。
2.单元测评命题的双向多维细目表
下面节选其中的3种题型,分别具体说明如何设计双向细目表和命制试题。
(1)数列单元测评双向多维细目表。(见表1)
(2)数列单元测评部分试题的命制与意图。
例题1:数列{an}为等差数列,Sn为其前n项和,已知a7=5,S7=21,则( )。
A.a1=1
B.d=
C.a2+a12=10
D.S10=40
本题主要通过数学问题情境评价学生对等差数列的通项公式与前n项和公式的掌握程度,通过运用求基本量的方法和方程思想评价学生的运算求解能力。
例题2:将数列{4n-2}与{6n-2}的公共项从小到大排列得到数列{an},则{an}的前8项和为______。
本题主要通过数学问题情境评价学生对两个等差数列公共项的理解程度,以及等差数列及前n项和公式掌握程度,通过特殊到一般的思想评价学生的运算求解能力及逻辑推理能力。
例题3:已知正项等比数列{an},a1=1,a5=4a3。
(Ⅰ)求{an}的通项公式;
(Ⅱ)记Sn为{an}的前n项和,若Sm=63,求m。
本题主要通过数学问题情境评价学生对等比数列的通项公式与前n项和公式的掌握程度,通过运用求基本量的方法和方程思想评价学生的运算求解能力。
3.数列单元测评数据分析
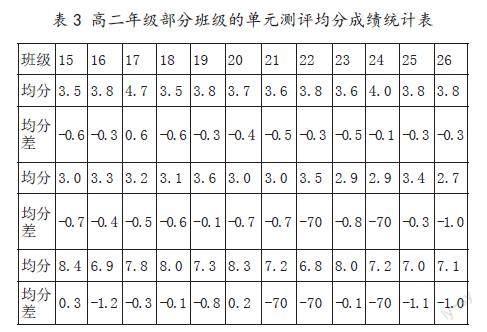
(1)数据呈现(表2、表3,表3见下文)。
(2)试卷难度与区分度的分析。这三道题主要考查等差、等比数列求通项、前n项和的基本方法,并考查学生逻辑思维能力和运算求解能力。从测评成绩的数据可以看出每道题的难度P值都在0.7以上,较为容易,表明试题难度控制得较好,符合单元测评的标准,且试题的区分度都大于0.3。
②区分度的常用指标为D,取值在-1~1之间,值越大区分度越好。测量学家伊贝尔认为:
(3)学生得分情况的整体分析。从三道题的得分可以看出,82%的学生可以掌握等差、等比数列求通项、前n项和的基本方法,但仍有18%的学生存在公式理解及运算方面的问题,在平时的学习中应该加强训练。课本的改编试题得分较低,说明学生对课本的习题重视不够,不能做到知识的迁移,建议教师在教学中注重课本例题、习题变式的讲解。
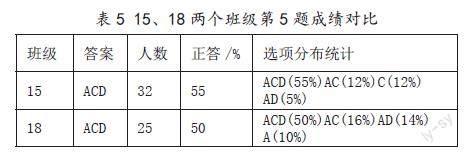
(4)各班平均分的对比分析。在表3中,15班、18班的例题1的均分皆为3.5分,从下表5的选项分布数据来看,原因主要是大多数的学生漏选或错选。说明学生在等差数列的通项公式、前n项和公式的理解应用以及运算能力等方面有欠缺,建议教师在平时的教学中引导学生加强公式的理解和运用,提升学生数学运算的能力。
如表3,对于例题2,23班、24班、26班的均分都低于3分,这说明学生对于课本上的课后习题尚未完全掌握,建议教师在课堂教学中多注重课本的习题讲解及培养学生的逻辑思维能力。
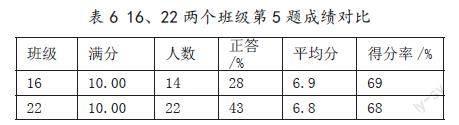
例题3的分值是10分,而表3中16班、22班的均分低于7分,说明学生对于等比数列公式的掌握程度不够,运算能力在平时的教学中需要加强。从下表5的两班对比来看,22班对于等比数列通项公式的掌握情况存在两极分化的现象,建议教师在平时教学中多关注基础薄弱的学生。
表6 16、22兩个班级第5题成绩对比
单元测评是一种非常好的过程性评价方式,是以学生为中心的测评形式。对学生而言,需要在单元测评之后,合理利用测评的结果,找到目标差,及时进行查漏补缺。对教师而言,单元测评设计应从单元核心知识入手,可以依照“命题—测评—诊断—反馈—改进”的步骤实施,体现了教、学、评一体化。
通过实践可以看到单元测评对学习的改进和对教学的改进都有重要意义,因此在高一、高二数学学习阶段应将单元测评纳入到单元教学的整体中,使之成为单元学习后的学业评价不可或缺的重要环节。
【参考文献】
[1]中华人民共和国教育部.普通高中数学课程标准(2017年版2020年修订)[S].北京:人民教育出版社,2020.
[2]喻平.数学核心素养评价的一个框架[J].数学教育学报,2017(2).
[3]喻平.基于核心素养的高中数学课程目标与学业评价[J].课程教材法,2018(1).
[4]王成杰,刘新春.关于数学模块测评评价的思考[J].中学数学月刊,2011(6).
(基金项目:本文系海南省教育科学规划专项课题“指向学科核心素养的高中数学单元学习质量评价研究”的阶段成果,课题编号:QJH202110059)

