思维生长：数学“板块题组”设计策略探究

金建忠 吴秋霞

【摘 要】习题练习在数学教学中起着至关重要的作用，但习题内容单一、形式单调、练习单向等问题制约了学生数学思维的发展。为此，本文论述在数学教学中，利用“板块题组”通过“内容交织”“方法适切”“练习启迪”三个设计策略实现在解决问题的过程中促进学生思维生长的目标。

【关键词】“板块题组” 思维生长 设计策略

在数学教学中，如果说例题是学生学习知识的纽带，那么习题练习就是学生形成技能的盘石。在教学实践中，笔者发现，很多学生对于数学基础题的解决比较顺利，但当题目出现变式、程度加深时却一筹莫展，这在一定程度上影响了学习思维的发展。分析后主要原因有：一是数学习题设计内容单一，缺少思维训练；二是数学习题设计形式单调，缺少变式训练；三是数学习题设计练习单向，缺少深度思考。

而“板块题组”可以很好地解决上述问题，让学生学会迁移，实现学习进阶。那么，如何设计“板块题组”至关重要。我们可以从“内容交织”“方法适切”“练习启迪”三个策略去设计“板块题组”，实现在解决问题的过程中促进学生思维生长。

一、思维“由浅入深”伸展：“板块题组”“内容交织”设计策略

（一）“交汇”——层次与坡度共推

在教学中，教师可以把练习题按内容分为三个层次：第一个层次是基础练习，使学生初步形成技能；第二个层次是拓展练习，使学生巩固技能；第三个层次是思维训练，使学生发展技能。这样能使练习适应学生的个别差异，使每一个学生都能得到发展。如在“分数乘除法”练习中，教师可设计以下题组（见图1）：

第一组是基础训练题，使学生形成基本的分数（小数）乘除计算技能；第二组是拓展训练题，使学生通过计算发现规律，再运用得到的规律编题，计算即巩固技能，编题即拓展技能；第三组是思维训练题，使学生通过观察数据特点、符号特点和乘法分配律的数学模型合理选择数据，组成多个符合要求的算式，在解题过程中既巩固技能又训练思维。

（二）“交融”——形式与思辨并行

学生对于练习题的接受度还在于练习形式的变化上，因此，教师在设计练习题组时要注意对同一项知识或技能的训练，设计形式多种多样的练习，这样就能激发学生的学习兴趣，更能从不同的角度培养学生的逻辑思维能力。如在学习“百分数的意义”时，教师可以设计这样的题组：（1）首饰的含金量一般用“12K”“18K”“20K”“24K”等表示，24K表示足金，12K表示含金量50%。如果一件质量为60克的首饰中，金的含量大约有51克，你认为这件首饰的含金量用多少K表示比较合理？（2）一件质量为60克的20K的首饰中，金的含量大约是多少克？题目创设了一个非常真实的情境，形式新颖，但又非形式化，此题对学生提高解决问题的能力非常有益，是“百分数意义”在新的情境中的应用，关注的是综合运用知识解决实际问题，知识的核心是百分数的意义，能力的核心是数量关系的分析，核心价值在于思考与辨析能力的提升。

（三）“交互”——开放与探究共存

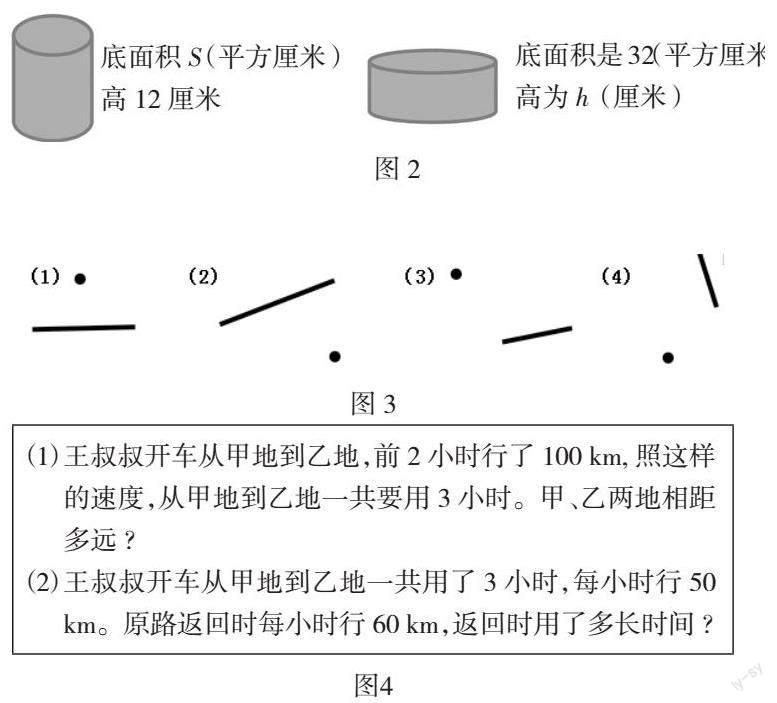
所谓“开放型练习”，其实是相对于条件完备、结论确定的封闭性的问题而言的，它的特征是一般没有现成的算法与确定的答案，要求学生善于联想、敢于创新，具备灵活运用知识的能力，能使思维辐射到与问题相关的一些知识点上。如在“比例”的教学中，教师可以设计这样的题组：下面两个圆柱的体积相等，请你根据题中提供的信息解决两个问题，一是求比值S：h;二是写出两个比例。（见图2）

本题表面上看似乎是在考查学生图形与几何的体积计算知识，实质是借用体积计算的方法指向比例的基本性质，需要学生有较高的思维灵活性和知识变通、创新应用的能力。题目要求写出两个比例，显然只能用题目给出的四个数据，根据比例的意义，必须是两个比的比值相等才能组成比例，但题目中给出的四个数据中有两个是字母，无法得到明确的比值。所以，我们必须改变思路，根据两个圆柱的体积相等，可以得到等式：12S=32h，于是，我们可以根据这个等式写出8个比例，选择其中任何两个都是正确的，S与h比值问题也就迎刃而解。

二、思维“由点到面”卷入：“板块题组”“方法适切”设计策略

（一）“串联”——融会知识脉络

在数学练习中，其实很多习题存在着相似或是相近的现象，有些甚至可以用同一个“模型”表示，以这些知识点为载体进行题组设计，把相似的习题编排在一起，就能将若干知识点串联起来，化零散为整体，使之系统化、结构化。教师把一些形同质异、形异质同等系列题组“串联”在一起，可以使学生对知识的理解由浅入深、由表及里，也可以很好地训练学生的审题能力，使学生逐渐把握知识，培养较强的思维能力和形成良好的思维品质。教师可以在知识关键处设计，可以在知识易混处设计，也可以在知识的重难点处设计等。

（二）“变换”——探究深层纹理

我们所说的变式，其实就是创新，通过变换条件或形式多角度设计题组，使学生多一些比较和甄别的历练，可以有效地突出知识的核心及外延。当然，变式不是盲目地变，应遵循学生认知规律，根据实际需要进行变式。在设计变式题组时，教师应抓住思维训练这条主线，恰当地变更问题情境或改变思维角度，培养学生的应变能力。如教学“点到直线的距离”时，对于课堂中的例题，学生能很好地理解；对于一般的习题，学生也能很好地掌握。但画图本来就是数学学习中的一大难点，稍有变化，学生就会无从下手，原因就是学生所学、所练、所画形式单一，缺少变化，多为机械操练。因此，教师可以增设以下题组（见图3）：

（三）“挖掘”——发现潜在价值

教材是众多专家学者以及一线教師集体智慧的结晶，而数学习题又是数学教材的重要组成部分，每一道习题都有着它本身特有的价值。作为教师，我们要认真研读教材，充分理解教材意图，合理定位教学目标，认真界定内涵与外延，仔细研究，大胆“挖掘”，善于发现这些习题的训练价值，进行拓展与延伸性设计题组。如教材中有这样一题（见图4）：

（1）王叔叔开车从甲地到乙地，前2小时行了100 km，照这样的速度，从甲地到乙地一共要用3小时。甲、乙两地相距多远？

（2）王叔叔开车从甲地到乙地一共用了3小时，每小时行50 km。原路返回时每小时行60 km，返回时用了多长时间？

显然，这是一组正、反比例的解决问题题组，教材通过对比的方式用相同素材和相近信息，编出一组正、反比例的题，这样的编排更有利于学生对比、判断并正确解答，从而提高判断能力和解决问题的能力。据此，教师可以让学生自己适当改变题中信息进行改编，如王叔叔前2小时行了100千米，后来又行了3小时，照这样计算，一共行了多远？……也可以启发学生编写对比题组，如：（1）用边长2分米的方砖铺一间会议室，则需要450块，如果用边长3分米的方砖来铺，需要多少块？（2）用同一种方砖铺地，30平方米的会议室铺了60块，那么100平方米的阅览室要铺多少块？这样的“挖掘”、拓展和延伸意义非同寻常，价值不可小觑，效果不言而喻。

三、思维“由静变动”跃迁：“板块题组”“练习启迪”设计策略

（一）“变式”——叩启求异思维

在数学学习中，学生常常会出现思维定式，即总是按照某种习惯的思路去思考问题，这样不利于问题的解决，更不利于思维灵活性的提升。在数学教学中，教师可以用对比性的题组叩启学生的求异思维。例如，请你用合理的方法计算“350×18”和“600÷25”，本题组通过“一乘一除”一组对比題，考查学生的多位数乘除法计算，命题立意指向能力，即思维与方法的灵活多样及运用运算定律和性质进行计算的能力，既可以考查学生基本计算方法的掌握情况，又可以考查学生灵活运用计算知识，追求计算方法合理、简便的意识与能力，给不同水平学生创设了很大的思维空间。这两道题都可以用不同的方法计算出结果，并且不同水平的学生可以有不同的方法。方法虽有许多种，但思考、甄别、判断和选择的过程才是题组的精髓和价值所在。

（二）“再造”——叩建思维体系

以生为本再造数学练习，让学生尽可能多地自主学习，感悟、交流、发现、质疑，主要依靠学生自己生成知识和能力。教师进行习题再造，设计“板块题组”，引导学生在练习过程中沟通知识之间的联系，建构思维体系。例如，在学生初步认识圆柱后，他们已经知道圆柱由两个圆和一个侧面（长方形或平行四边形）组成，教师提问学生，除了两个圆配以合适的长方形或平行四边形之外，还有其他方法可得到圆柱吗？学生通过讨论想到长方形旋转也可以得到圆柱。于是，教师出示题组（见图5）：

（1）长12厘米、宽5厘米的长方形分别以长边和宽边为轴旋转一周，得到的圆柱的尺寸分别是怎样的？请你分别写一写，再想一想，两个圆柱大小一样吗？（2）这里有一个三角形和一个梯形，你想象下它们旋转后又会变成怎样的立体图形，请你画一画。

这样的题组设计，打破了学生认识圆柱的局限，对于学生空间观念的发展尤为重要，但如果仅仅满足长方形旋转形成圆柱，定位太低；紧跟着，“分别以长边和宽边为轴旋转一周，得到的圆柱的尺寸分别是怎样的？”“两个圆柱大小一样吗？”两问提升了观察、比较、空间想象等能力；最后，教师让学生想象并画三角形和梯形旋转后的图形，显然让学生对知识的理解、对空间的感悟达到了新的高度。当然，最有价值的是，学生对于圆柱的认识更为全面，对于立体图形的认识更为深刻，由点到面，形成知识体系。

（三）“散聚”——叩响思维跳跃

设计题组应当事理相同，思路相通。在学生做完题目后，教师应该引导学生从发散的题型中聚拢知识的本质属性，进一步抽象概括出这类题目的特点和解题思路，揭示出其内在规律，提升思维。（百）分数应用题题型千变万化，错综复杂，一些学生对其无所适从、无从下手。其实，这类题目也是有章可循、有法可依的。教师在教学中可设计如下题组：

（1）一本书共90页，小可已经看了1—5，已经看了多少页？

（2）小可看一本书，已经看了1—5，正好看了90页，这本书有多少页？

（3）小可看一本书，已经看了1—5，还剩90页，这本书有多少页？

（4）小可看了90页，比小爱多看了1—5，小爱看了多少页？

（5）小可看了90页，小可与小爱看书的页数比是3：2，小爱比小可少看百分之几？

（6）小可3小时看了90页，这时已读页数比剩下页数多1—5，照这样的速度，小可还要几小时才能读完这本书？

设计这一题组，其出发点是让学生在练习过程中进行渗透、对比和概括，引导学生抓住特征，理解本质，提炼方法——找相等关系，实现“练一组，通一类，增智提能”的初心。

【参考文献】

[1]巴黎.如何实现小学数学的深度教学[J].教育，2019（18）.

[2]吴烈.核心问题来引领 题组练习显“神威”——浅谈小学数学题组练习的设计与思考[J].小学教学研究，2017（16）.