K-12教育中通过编程培养计算思维的导图绘制

克里斯蒂娜·提克瓦 埃夫西米澳斯·坦布里斯

摘 要：通过编程培养计算思维引起了越来越多的关注，该领域的学者认为，计算思维是发展21世纪技能的理想媒介，因此，世界各地都提倡K-12，相关研究迅速增加。然而，研究表明，关于计算思维的研究与教育实践中存在诸多挑战。此外，由于缺乏整体规划，人们尚未全面理解计算思维领域存在的挑戰及计算思维课程的发展。因此，本研究的目的是在系统文献综述的基础上开发一个概念模型，绘制K-12教育领域中通过编程培养计算思维的导图。基于对101项研究的综合分析和对计算思维领域的识别，本研究提出K-12教育中通过编程培养计算思维的概念模型。该模型包括6个计算思维领域（知识库、学习策略、评估、工具、因素和能力建设）及其相互关系。该概念模型有助于了解计算思维领域，并为未来研究打下基础。此外，该模型支持将计算思维整合进K-12教育实践中，为教育政策制定者和研究人员提供资料，并使研究、实践和政策结合得更加紧密。

关键词：计算思维；编程；K-12教育

中图分类号：B812.2 文献标识码： A 文章编号： 1004-8502（2023）01-0101-28

译者简介：胡多娇，华东理工大学硕士研究生，研究方向为翻译实践；宋帅，上海外国语大学贤达经济人文学院讲师，研究方向为英语教学和翻译；赵静洁，华东理工大学硕士研究生，研究方向为翻译实践；曲颖，华东理工大学硕士研究生，研究方向为翻译实践；李岩，华东理工大学外国语学院讲师，研究方向为英语教学。

一、引言

计算思维（Computational Thinking，CT）起源于20世纪80年代，由派珀特向年轻学生介绍编程时提出[1]。后来在2006年，温将计算思维定义为“通过借鉴计算机科学的基本概念来解决问题、设计系统和理解人类行为 ”的过程[2]。如今有学者认为，计算思维是每个人必备的技能[2]，是发展21世纪技能的理想媒介[3][4]。

过去约15年来，计算思维再度受到学界关注，该研究领域开始走向成熟。近年来，大量关于计算思维的研究发表[5]。许多研究表明，计算思维的一些特定领域存在诸多挑战，包括：第一，开发能够涵盖计算思维复杂性并能被广为接受的评估方法和框架[6-13]；第二，设计基于理论的方法，使学习策略与计算思维相匹配[14]；第三，确定教授计算思维所需的知识以及为教师提供支持的方法[15-17]。计算思维领域的全面导图可以使人们更好地理解现存挑战，并为未来的研究提供指导。

一些文献综述从不同角度审视了整个计算思维领域，并提出相关框架与定义。研究人员回顾文献，旨在通过K-12课程的编程深入了解计算思维 [4]，了解计算思维在教育中的发展和应用[5]，促进K-12课程中的计算思维学习和评估[18]，并支持教育者开发计算思维任务和程序[19]。尽管研究人员已做了许多努力，但仍缺乏计算思维领域的全面导图。

此外，为满足社会对21世纪技能的需求，世界各地都在努力将计算思维融入学校教育[20-22]。同时，许多正在实施的倡议通过提供课程建议[23]、计算思维和编程的工具与资源[24]促进计算思维的发展。然而，目前在K-12教育领域并没有通过编程培养计算思维的完整导图帮助教育工作者设计计算思维课程。一些研究强调，教师缺乏对如何将计算思维有效整合到K-12教育实践的清晰理解[3][8][17]。

推进计算思维领域研究并促进计算思维教育实践的一个方法是系统地研究现有文献，并创建一个该领域导图的概念模型。开发概念模型是“为了理解和交流而对我们周围物质世界和社会世界某些方面的活动进行理论描述”[25]。概念模型还有助于对相关领域进行推理，交流领域细节，记录领域信息以供将来参考，从而帮助人们加深对该领域的理解[26]。此外，概念模型可以为该领域知识的发展提供坚实基础，成为人们在已知和需知之间的有效指引[27]。K-12教育中通过编程培养计算思维的概念模型可以作为基础，帮助研究人员从整体上更好地理解该领域及其面临的挑战，并识别出已研究领域和尚需进一步研究的领域。此外，概念模型可以作为契合点[25]，通过为教师提供参考协助K-12教育中的计算思维教学。

本研究的目的是在系统性回顾文献的基础上开发一个K-12教育中通过编程培养计算思维的概念模型。这一模型有助于理解计算思维领域，并为未来研究提供参考，也有助于支持研究人员关注计算思维研究中的重大研究空白，拥有最新的相关文献整合资料。此外，它还支持将计算思维融入K-12教育实践，为教师和政策制定者提供资料，使研究、实践和政策结合得更加紧密。

概念模型的开发包括计算思维领域中的概念和关系识别及其可视化呈现[28]。对此，研究人员系统地回顾了有关文献，并记录了研究人员感兴趣的所有主题，如评估、支持教师的专业发展、相关工具等，这些在相关发表成果中已有讨论。然后，根据研究人员定义的计算思维领域将这些主题进行分组。最后，构建CTPK-12概念模型以呈现上述计算思维领域及各领域间的关系。

二、研究背景

计算思维是一种思维过程，涉及利用计算机科学（Computer Science， CS）的核心概念解决问题和设计模型系统[29]。计算思维借鉴了计算机科学的概念，但它是每个人的基本技能。温认为，“除了阅读、写作和算术，我们还应将计算思维植入每个孩子的分析能力中” [2]。阿霍将计算思维定义为“阐述问题时所涉及的思维过程，因此，问题的解决方案可以表示为计算步骤与算法” [30]。相关文献中还有许多对计算思维的不同定义。

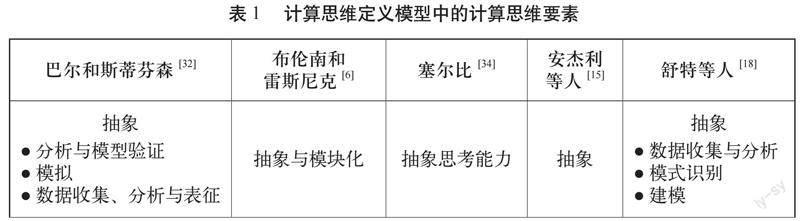
计算思维的定义可分为两大类：一类是通用定义，侧重于将计算思维视为一种思维过程[31]，另一类是描述计算思维所包含内容的定义模型。后者包含计算思维要素模型的开发过程。例如，巴尔和斯蒂芬森的模型是在多学科背景下提出了计算思维的概念和能力[32]。安杰利等人开发了一个描述计算思维技能的概念框架[15]。美国计算机科学教师协会和美国国际教育技术协会提供了计算思维的操作定义，描述了计算思维的特征和看法[33]。塞尔比的定义模型描述了计算思维的思维过程[34]。温托宾等人开发了一个呈现计算思维实践的模型[35]。布伦南和雷斯尼克的计算思维框架描述了计算思维的概念、实践和观点[6]。舒特等人开发了一个可用于评估计算思维的能力模型[18]。卡列利奥格鲁等人构建了一个描述计算思维技能的框架，并认为计算思维是一个解决问题的过程[19]。张和努里扩展了布伦南和雷斯尼克的框架，将计算思维技能纳入其中[6][36]。一些定义模型对计算思维要素的描述摘要如下（见表1）。由于文献中引用了大量模型，这些模型时间跨度较大，且采用的研究方法各不相同（例如，系统的文献综述、作者既往研究、文献综述、会议论文集等），因而本研究将有选择地对具体模型进行介绍。

虽然有关文献不只探讨了编程这一种方法，但编程与计算思维紧密相关[37]。然而，二者之间的具体关系并不明确[22]。基于已知见解，一方面，编程为执行计算思维的概念和实践提供了必要的机制[6][38]，是完成有关计算思维认知任务的关键工具[3]；另一方面，計算思维也为编程提供了一个新的方向，使其成为理解数字世界的一种手段，同时促进K-12教育环境中的编程教学[4][39]。计算思维和编程之间这种双向关联可以描述为：编程支持计算思维的发展，而计算思维也赋予编程全新的作用。

将计算思维融入课程是世界上许多国家的一个重要目标[40]。在美国，大多数计算机科学课程涉及计算思维概念，如问题分解、调试、抽象和算法[10]。以色列的课程让学生接触计算思维，目的是向学生介绍逻辑和算法思维[41]。其他国家也在推动将计算思维融入课程，比如波兰、新西兰、爱沙尼亚、芬兰、瑞典、挪威和韩国[40]。

近年来，有关计算思维的文献综述越来越多，这也表明人们对计算思维的浓厚兴趣。其中一些综述侧重于计算思维领域的某个特定主题（比如技术或评估[42][43]），而另一些则涉及多个主题。涵盖多个主题的综述可分为三类：第一类，旨在开发定义模型的研究（如卡列利奥格鲁等人[19]）；第二类，通过文献综述为计算思维教学提供见解的研究[3][4][20]）；第三类，旨在分析计算思维的研究[5]。尽管这些文献回顾了在K-12教育中通过编程培养计算思维的各个方面，但依然没有建立起计算思维领域的概念模型。

三、研究设计

（一）研究目标与研究问题

本研究的目标是开发一个反映K-12教育中通过编程培养计算思维的概念模型。该模型旨在描述计算思维领域以及各领域之间的关系。关于国家课程的政策和问题等将计算思维融入K-12教育的条件不属于该模型的范围。

研究问题包括：

问题1. 在K-12教育领域中，通过编程培养计算思维的领域有哪些？

问题2. 每个计算思维领域有哪些子领域？

问题3. 各计算思维领域之间是如何相互关联的？

（二） 研究方法

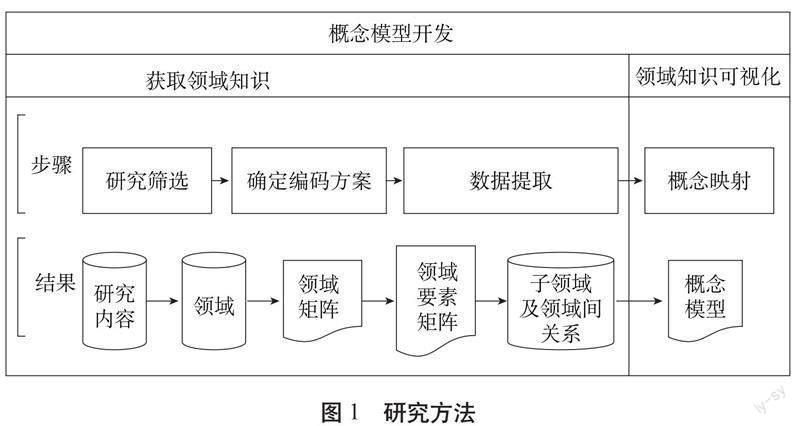
为了开发反映K-12教育中通过编程培养计算思维的概念模型，本研究采用了万德和韦伯提出的两个步骤：第一，获取领域知识；第二，将领域知识可视化[28]。图1为研究方法，展示了研究步骤和相关研究结果。研究人员采用韦伯斯特和沃森[27]的系统文献综述法来获取领域知识（计算思维领域及各领域间关系），包括识别计算思维来源的结构化方式和以概念为中心的结果呈现方法。首先，研究人员在研究选择阶段采用PRISMA声明（系统综述和元分析优先报告规范）[44]。然后，在编码方案确定阶段确定计算思维领域，作为在数据提取阶段的编码方案。数据提取阶段的目的是确定每个计算思维领域的子领域以及各计算思维领域之间的关系。最后对数据提取阶段的结果进行可视化操作。整个研究过程演变为迭代阶段，过程中产生了许多尚在分析中的新研究，从而对计算思维领域、子领域及其相互关系进行修订。下文将进一步阐述本研究所遵循的步骤。

1. 获取领域知识

（1）研究筛选

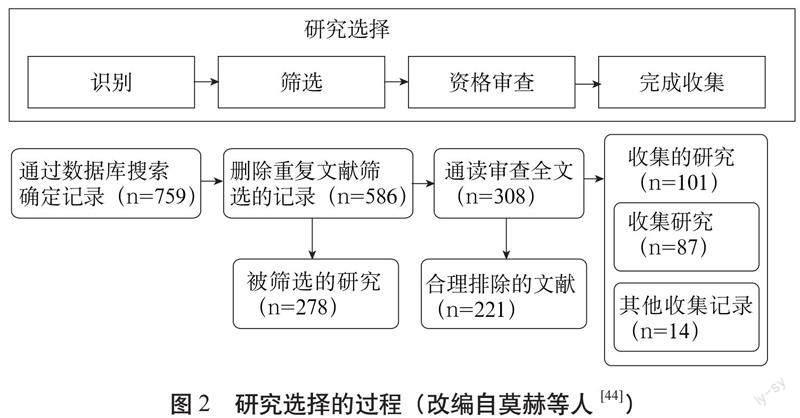
本研究采用PRISMA声明进行研究选择（见图2）。具体来说，本研究按照韦伯斯特和沃森的提议[27]，通过考察选定研究进行识别，据此调整PRISMA流程图（图2），将额外记录归进纳入阶段。

对纳入综述的研究的选择是决定综述有效性的一个关键因素。为此，研究人员共同确定了搜索关键词和标准，但各自独立进行研究筛选及应用文献纳入和排除标准。这一过程中出现了一些问题，但都通过讨论得以解决，并最终达成一致。该阶段的研究结果在补充材料中有详细介绍（所有补充材料都列在附录B中）。

以下内容对研究选择阶段的子步骤进行了概述。

①识别。利用科学数据库Web of Science和Scopus中的关键词检索相关研究。具体来说，本研究搜索了“计算思维”这一短语（包括引号），并将时间限制在2006年以后。选择2006年这一时间节点是因为温在2006年重新提出了“计算思维”这一术语。在Scopus中，本研究的搜索范围包括标题、摘要和关键词；在Web of Science中，本研究将类别限定为教育研究。在Web of Science和Scopus数据库中，本研究只搜索了文章和述评。保持上述搜索条件，搜索工作从2018年3月持续到2019年10月，共计3次，筛选出759项研究，其中499篇文章来自Scopus数据库，260篇文章来自Web of Science数据库。

②筛选。删除173个重复研究后，对上一子步骤检索得到的研究进行筛选。研究人员阅读了所有的标题和摘要，并删除了非英语研究或无法获得全文的研究，同时排除了短篇论文。该子步骤结束后，还剩下308项研究。

③资格审查。这一子步骤检查全文并采用以下文献纳入和排除标准，进一步检阅了筛选步骤中检索到的研究。

文献纳入标准如下：第一，研究应发表于期刊；第二，研究可以是概念性论文、观点性文章和实证研究，因为除实证研究外，概念性论文包括理论框架和未来方向，纳入此类论文可以扩大综述的范围；第三，研究重点应为K-12教育中的计算思维，且涉及编程；第四，如果是实证性计算思维研究，参与者应为K-12学生、K-12职前教师或K-12在职教师。

文献排除标准，即应排除有如下情况的研究：第一，没有专门关注K-12教育中的计算思维，如关注高等教育的研究；第二，没有专门关注通过编程培养计算思维，如研究方法侧重于有形工件、桌游、展品等；第三，只在引言或研究背景部分提到计算思维，而在研究结果中并未提到计算思维，或测量的是其他东西而非计算思维。

④完成收集。随后，通过审查其引文（向后）和确定引用过它们的文章（向前）进一步筛选这些研究。通过这一研究步骤，又收集了14项额外研究，包括2份灰色文献资料。最后，共有101项研究被纳入此次研究范围（附录A）。

（2）确定编码方案

为确定K-12教育中通过编程培养的计算思维作为本研究的编码方案，我们使用了传统内容分析法。当现有的理论有限且不采用预设的编码方案，而是通过文本分析导出编码方案时，建议采用传统内容分析法[45]。本研究选择传统内容分析法，正是因为缺乏描述计算思维领域的概念模型。一开始，我们通读了所有文献，以便从整体上了解计算思维领域。然后仔细阅读了每一篇文献，并关注指代某个概念/领域的关键词。接着将关键词进行组合，提供编码方案的类别。例如，对关键词“评估计算思维的发展”“评估”“评估和评价”“评估”进行归类，最终在编码方案中加入了“评估领域”。最后，我们根据这些类别将研究进行分类，通过增加新的类别或合并与拆分现有类别，不断完善编码方案，以确定最终编码方案的类别。此后，这些类别被称为计算思维领域，并作为编码方案和概念模型的概念。

因此，我们编制了一个概念矩阵，也称计算思维领域矩阵，该矩阵列出了每篇文献所对应的计算思维领域。正如韦伯斯特和沃森所建议的那样，我们通过这种方式使研究方法从以作者为中心过渡到以概念为中心（见表2）。

（3）数据提取

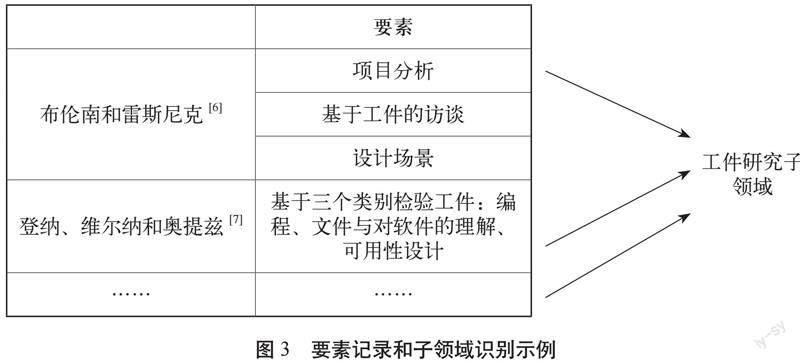
在这一阶段，我们将所选的研究按编码方案进行分类，并使用表格记录补充材料中的每个计算思维领域（附录B）。在将一项研究插入表格时，我们也记录了该研究中出现的领域要素（见图3）。随后，将每个要素与其他所有要素进行比较，与其他要素明确匹配的要素又可以构成一个子领域。例如，在评估领域中，“项目分析”与“检查工件的计算思维模式”两个要素包括在“工件分析”这一子领域中。只包含一个要素的子领域和低频（<2项研究）子领域仅在补充材料（附录B）中列出，未被纳入模型中。

随后，我们针对每个计算思维领域建立表格，记录能够证明各子领域（见图4）和各领域间关系的证据。然后，对记录数据进行分组，最终总结出各领域间的关系。

2. 领域知识可视化

在这一步，我们采用锡奥和谭提出的概念导图[46]，将概念（计算思维领域）和领域间的关系可视化，其确定过程已在“获取领域知识”部分详述。我们创建了一个可视化的概念模型，将计算思维领域设定为节点。在每个节点上，我们会关注前一阶段所确定的各计算思维领域的子领域。最后，将计算思维领域之间的关系用链接表示，然后对每个链接进行标记以解释它们之间的关系。

（三）研究的局限性

本研究存在一定局限性。第一，本研究所提出的模型只以对英文文献的分析为基础。第二，本研究只在两个科学数据库中进行了搜索，即Web of Science和Scopus。第三，本研究的搜索只包括在期刊上发表的文章。尽管我们最终纳入了一些会议论文和灰色文献（我们对所选研究的参考文献进行人工检索，确定了这些灰色文献），但大部分入选文献仍然是期刊文章。第四，本研究搜索设置的时间范围限制在2006年以后。因此，该模型完全基于2006年至今的研究，并未考虑计算思维研究的初始阶段。第五，本研究没有纳入所有符合质量标准（见“资格审查”部分）的研究，因此无法对所有已开展的研究进行详尽介绍。最后，本研究带有主观性，且参与研究者数量较少（只有两位）。尽管本研究采用了系统的方法（详见“研究方法”部分），但仍需在以下方面作出主观选择：例如，对要素进行分组、根据记录的证据定义关系、为计算思维领域和子领域命名以及确定最终包含在模型中的子领域的排除标准。

四、研究结果

（一） 确定计算思维领域

在编码方案确定阶段，我们对101项研究进行了分析，确定了6个计算思维领域（见表3）。补充材料（附录B）中提供了计算思维领域矩阵，我们在其中记录了各计算思维研究包含的领域。计算思维研究试图解决K-12教育中通过编程培养计算思维所面临的问题，重点关注在所选研究中反复出现的领域。

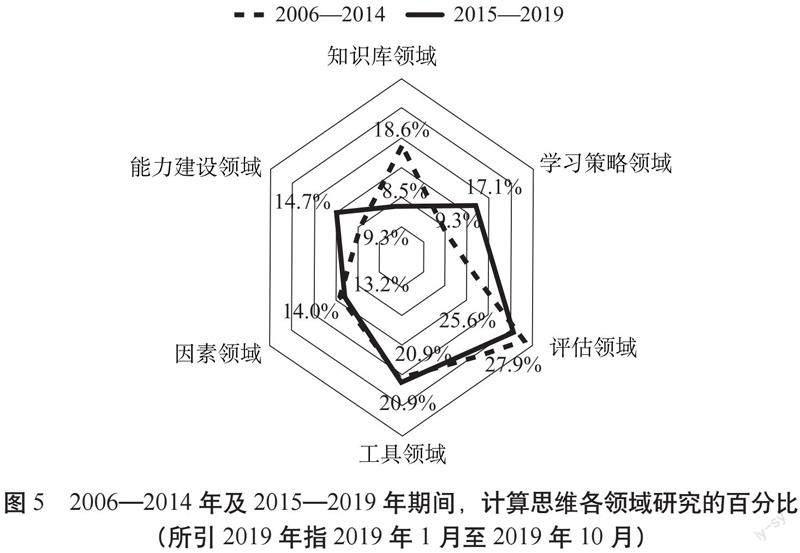
计算思维各领域研究所占的百分比见图5。我们将这些研究按照时间分为2006—2014年和2015—2019年两个组。如图5所示，“评估”和“工具”是两个最受欢迎的领域，学者在这两个时期均对其有濃厚的研究兴趣。评估领域在两个时期中都排在第1位（2006—2014年期间为27.9%，2015—2019年期间为25.6%），其次是工具领域（两个时期均为20.9%）。在2006—2014年期间，知识库领域排在第3位（18.6%），而在2015—2019年期间，旨在定义计算思维的研究比例降至8.5%，知识库领域成为学者最不感兴趣的领域。相反，专注于学习策略的研究比例从2006—2014年期间的9.3%增长到2015—2019年期间的17.1%，学习策略领域成为所选研究中第三大受欢迎领域。对于能力建设领域，专门针对该领域的研究比例从2006—2014年期间的9.3%增长到2015—2019年期间的14.7%，能力建设领域的受欢迎度位于第4位，其次是因素领域。这些结果表明，随着计算思维领域的发展，相关研究仍然集中在“评估”和“工具”领域，但关注的重点已不仅限于计算思维的定义，而是转向更具体的问题，如学习策略、能力建设和因素。

（二） 计算思维领域

1. 知识库领域

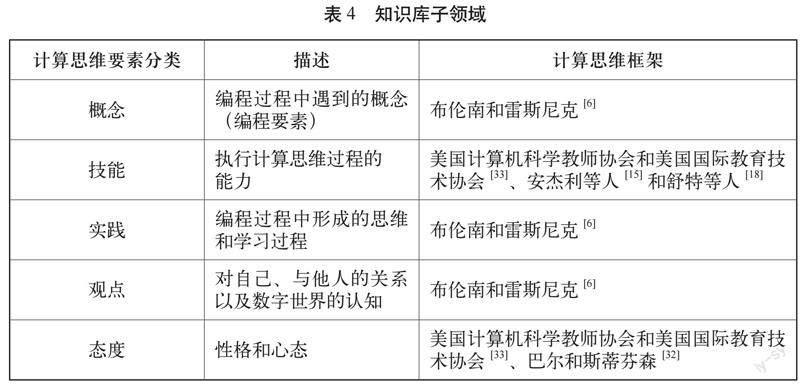
知识库领域是计算思维领域的核心，101项研究中有57项属于这一领域。在这些研究中，研究人员或提出一个框架或定义来识别和分类计算思维的可测量要素，或简单地评估计算思维要素以评估计算思维。本研究基于计算思维框架考察了所选研究中的计算思维要素，并将知识库领域分为5个子领域：概念、技能、实践、观点和态度（见表4）。

在选定的研究中，计算思维知识库分析结果包括各种计算思维要素和描述计算思维要素分类的术语，例如技能、能力、观点、态度、实践、特征、概念、方面和思维过程。其中，一些术语通常有不同的含义。

此外，若干计算思维要素，如抽象、算法、分解、数据表征、测试、评估、调试、概括、迭代，似乎具有多种分类方式，包括计算思维技能、计算思维概念、计算思维实践或思维过程。例如，抽象分别被归为“抽象思考能力”的思维过程[34]、“决定保留和忽略关于实体/对象的哪些信息的技能” [15]，以及抽象和模块化的实践，即“通过将较小部分的集合放在一起构建较大的事物” [6]。

根据布伦南和雷斯尼克的框架，对选定研究的分析揭示了以下计算思维实践：测试与调试、再混合和再利用代码、增量与迭代、抽象与模块化。此外，登纳等人提出的可用性设计、代码组织和文档以及编程效率等要素也很明显是进行计算思维的关键能力[7]。

布伦南和雷斯尼克定义的计算思维概念在本研究中反复出现，包括序列、条件、环路、事件、并行化、变量（数据）和操作符。布伦南和雷斯尼克的框架中未包含的功能、同步块和用户交互块也在本研究中有明显体现。在选定的实证研究中，研究人员经常将这些计算思维概念与其他计算思维要素相匹配[12][47]。例如，冯·瓦根海姆等人将Snap中多个脚本的使用和自定义块的定义视为抽象化[47]。

通过回顾这些研究，我们发现了逻辑、协作、合作、问题解决、创造力、沟通、批判性思维、自我效能等要素。这些要素出现过1～2次，没有被纳入计算思维框架中。这些要素的存在是可以解释的，因为有研究人员采用一些经过验证的通用评估方法对其进行了评估[12][48]。也有其他研究采用了这些通用评估方法[49-55]，导致这些要素大量存在于我们回顾的实证研究中。

计算思维态度和观点在回顾的研究中出现的频率较低，主要包括布伦南和雷斯尼克所述的“连接”和“表达”[6]。

2. 评估领域

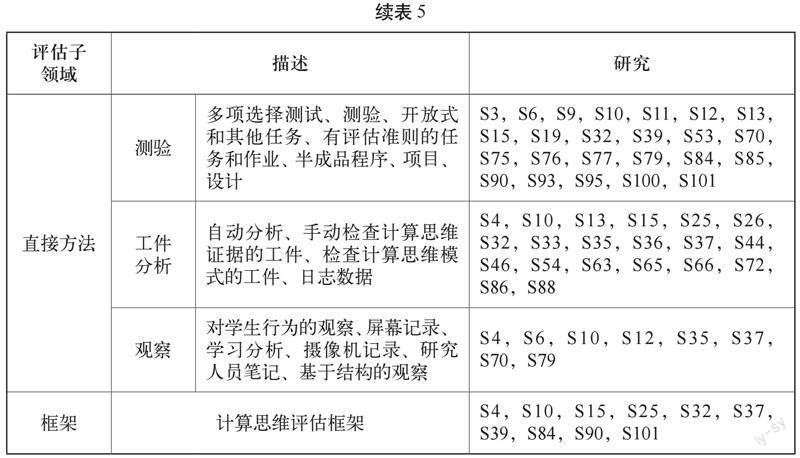
有53项研究对计算思维评估领域进行了考察。在所选研究中，研究人员开发并验证了评估方法，提出框架或测量学生的计算思维水平，以便通过各种评估方法深入了解学生的学习情况[9]。本研究将评估领域分为5个子领域：自我报告法、测验、工件分析、观察和框架。其中，测验、工件分析和观察直接测量计算思维，与通过记录自我反思来间接测量计算思维的自我报告法相反。表5列出了评估的分类。

所选研究中的计算思维评估方法主要基于每项研究的具体内容。然而，也有學者致力于开发通用评估方法，比如开发和验证用于计算思维评估和自动工件分析工具的测验和自我报告量表[12][31][48][56-59]。工件分析通过检查学生的程序来检测计算思维存在的证据。自动工件分析能让教师和研究人员将重点放在观察和访谈等评估方法上，以便更全面地获知学生的理解水平[43]。

评估框架通常能够给出评估方法的最佳组合。已经提出的框架涉及数据挖掘技术、假设驱动的方法和以证据为中心的设计方法[10][60][61]。

3. 学习策略领域

回顾发现，有37项研究涉及学习策略。研究人员将最常见的学习策略领域分为6个子领域：基于游戏的相关策略、基于建模和模拟的相关策略、问题解决相关策略、基于项目的相关策略、脚手架相关策略和协作相关策略（见表6）。脚手架相关策略被分为一个单独的子领域，因为选定的研究特别强调脚手架相关策略。其他策略还包括动手实践、通过媒体设计进行美学设计、讲故事和引导发现。

另外，研究显示，关注学习策略的研究或提出了计算思维的教学框架，或通过应用学习策略激发学生培养计算思维。其中许多策略都与基于皮亚杰建构主义理论的建构主义和/或维果茨基的“最近发展区”[62][63]有关。此外，学习策略在传统课堂环境、远程或混合环境中实施[11][38]，利用了教师指导和虚拟学习环境提供的服务。在选定的研究中，研究人员经常同时使用多种学习策略以充分发挥各策略的优势。在关注学习策略这一领域的37项研究中，有15项应用提出了一种以上的学习策略。

4. 因素领域

有22项研究讨论了与计算思维相关的因素。我们将因素领域分为2个子领域：人口因素及认知与非认知因素（见表7）。人口因素在所选研究中最为突出，22项研究中，有17项讨论了学生的性别，7项讨论了学生的年级。

有几项研究探讨了计算思维和学生年级之间的关系。其中一些研究表明，计算思维习得与年级（或年龄）无关[64][65]。另外几项研究认为，计算思维习得与年级（或年龄）之间存在显著相关。然而，这些研究对二者关系类型的结果却存在着矛盾。一方面，一些研究表明，年级或年龄与计算思维之间存在着正相关关系。更具体地说，罗曼·冈萨雷斯等人使用计算思维测验评估了1251名学生的计算思维水平并得出结论：计算思维水平随着年级的增加而提高，因此表明这一发现可能与计算思维在认知问题解决方面的作用有关，与杜拉克等人报告的研究结果一致[31][49]。另一方面，也有研究证明，年龄（年级）和计算思维之间呈负相关关系。更具体地说，杜拉克和萨里特佩奇发现，年级对计算思维呈负向预测关系，即随着学生年级增加，他们的计算思维水平会受到负面影响[66]。然而，他们指出，这一发现可能与研究参与者之前的经历有关，年级不同，经历也不同。孔、邱和赖也报告了计算思维（编程授权要素）与年级之间的负相关关系[57]。然而，作者强调，其他因素（如个性化教学的减少和难度水平的差异）可能会影响学生的计算思维习得。以色列·菲舍尔森和赫尔什科维茨进一步比较了不同年级学生在特定计算思维要素上的成绩[67]。他们强调，不同年级的学生擅长的概念不尽相同，这表明计算思维方法的设计应该考虑“计算思维概念和年级之间的匹配” [67]。

关于性别与计算思维关系的研究结果也相互矛盾。其中一些研究表明，计算思维习得与性别有关，而另一些研究发现性别和计算思维学习之间没有显著关联[64][65]。同样，认为计算思维与性别显著相关的研究也得出了相互矛盾的结论。其中一些研究发现，计算思维水平的分化对女性学生有利[49][66]，而其他研究则表明计算思维水平的分化对男性学生有利[31][57]。研究还讨论了与人口统计学因素（如性别、社会经济）有关的挑战，如在计算机科学方面表现不佳以及学习动机不强的问题[16][68][69]。

另外，所选研究中对创造力的探讨包括两种不同的研究角度。一些研究将创造力与其他要素一起归为计算思维的核心要素[13][48][59][70][71]，而其他研究将创造力作为一个独立的结构，单独研究其与计算思维的关系。参与努里、张和马尼拉等人研究的教师称，创造力是计算思维学习过程中出现的技能之一[72]。金姆发现，在参与计算思维干预后，学生的创造力有所提高[71]。相反，赫斯科维兹等人发现，计算思维和创造力之间没有关系，但他们认为这可能与所用学习平台的具体特征有关[73]。

所选研究对自我效能感的探讨也分为上述两种研究角度。罗曼·冈萨雷斯、佩雷斯·冈萨雷斯和莫雷·诺莱昂等人发现，计算思维与计算思维自我效能感呈正相关[74]。此外，他们认为，通过积极的个人学习体验培养学生的自我效能感或许是习得计算思维的有效途径。杜拉克等人也报告了计算思维和编程自我效能感之间的显著关系[49]。

所选研究中涉及的其他因素包括个性、毅力、对编程的态度和兴趣、对合作的态度、学业成就和对各学科的态度、学习编程遇到的挑战及教师的教学目标[57][66][67][74-76]。

所选文献还研究了认知因素，如语言、空间、推理、数字、解决问题的能力及思维方式和反思性思维[31][49][66]。

5. 工具领域

在47项研究中，研究人员使用或开发了计算思维教学和学习工具。本研究将K-12教育中通过编程进行计算思维教学的工具分为3个子领域：编程工具和社群、机器人和微控制器以及专为计算思维开发的工具。表8列出了工具分类。

在所选研究中，学生主要通过编程工具学习编程概念和实践。根据布伦南和雷斯尼克的观点，学生在编程过程中遇到的概念和实践也可以被认为是计算思维的概念和实践[6]。所选研究中记录的大多数工具都是可视化编程工具。此外，即使使用文本编程，也通常会用动画使其结果可视化。基于代理的编程范式也被广泛应用。此外，有研究人员提出社群这一工具，认为计算思维和编程是社会实践[39][77]。所选研究中的学生分享他们的程序并利用社群的社会化特征，按照邢的说法，社会化功能又可促进学生的计算思维发展[78]。

在部分所选研究中，机器人被用于计算思维教学，学生在编程机器人与环境互动的过程中会接触到计算思维的概念和实践。在其他工具中，教育机器人套件最为普遍[64][79]。在包含学生对自動化或复杂机器人设备编程的研究中，微控制器也是常用工具[49][80]。

一些研究通过开发工具支持计算思维理论框架或辅助课程。大多数开发的工具都是可视化编程工具，并涉及游戏玩法和/或建模[76][77][81-83]。

6. 能力建设领域

19项研究讨论了为教师提供指导和支持的问题。本研究将能力建设领域分为3个子领域：计算思维教学知识、教师教育和专业发展（见表9）。

规范计算思维教学知识是为教师提供帮助的前提条件[15][16]，因此，我们将其划为能力建设领域中一个单独的子领域。所选研究中的学者提出，要将技术教学内容知识（Technological Pedagogical Content Knowledge， TPCK 或TPACK）用于具体规范计算思维教学知识[15][84]。TPCK将技术知识（knowledge of technology， TK）、内容知识（knowledge of content， CK）和教育学知识（knowledge of pedagogy， PK）交织在一起[85]。安杰利等人将计算思维的TPCK定义为“使教师能够识别创新的、真正的计算思维项目的知识；能够识别为整个计算思维领域的实践/教学提供必要技术手段的技术；以及采用表征帮助所有人理解计算思维的知识”[15]。其他研究者将计算思维纳入技术知识中，建议教师应理解技术知识，并将其与教育学知识和数学、语言、艺术等学科内容知识建立联系[84]。

教师教育可将修订版教育技术课程作为基础，为职前教师提供习得计算思维的机会和方法课程。这些课程以教和学为重点，能够促进计算思维融入职前教师未来的教育实践[17]。根据这些研究思路，教师教育这一子领域的研究通过技术课程和方法课程向职前教师介绍计算思维[15][50][84][86]。例如，阿德勒和金姆将计算思维纳入为职前教师开设的科学方法课程[87]。大部分在模拟条件下感受计算思维的参与者（90%）认为，计算思维和模拟条件可以融入课堂中。例如，在加布里尔等人的研究中，参与者在Scratch中开发了项目，随后在实习期间将该项目运用到其教学实践中[50]。

专业发展旨在支持教师理解计算思维并将其融入教学实践中[88][89]。希克莫特和普列托·罗德里格斯提出，专业发展应该：第一，提供与计算思维学习工具和计算思维学习策略相关的活动；第二，包括循序渐进的练习和自我指导的项目；第三，考虑教师已有的知识；第四，提供可直接融入教学实践的资源；第五，通过直接评估方法评估教师的知识获取情况[90]。卡莱、阿克卡奥格鲁和卡伦等人认为，当专业发展侧重于计算思维在不同领域和问题解决中的应用时，教师可从中认识到计算思维的重要性并将所学知识融入教学中[91]。持续的专业发展包括研讨会、嵌入式辅导、行政支持、共同规划课程和共同教学，也可以为在职教师提供宝贵的帮助，从而扩展他们在计算思维中的参与[92]。

五、K-12教育中通过编程培养计算思维（CTPK-12）的模型

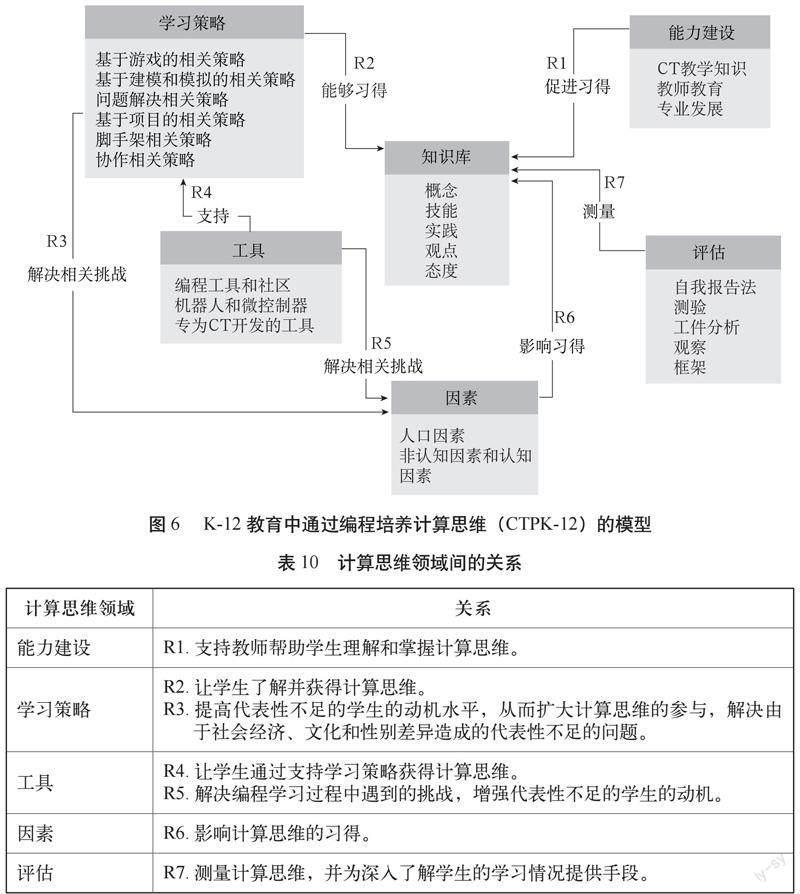
K-12教育中通过编程培养计算思维（CTPK-12）的概念模型（见图6）以提取的计算思维领域（如“计算思维领域”部分所述）及各领域间的关系为基础（见表10）。CTPK-12模型的关系体现了综述所选研究中发现的计算思维各领域间的主导关系。

R6和R7模型中的关系被认为是合理的，并在“计算思维领域”部分所描述的各计算思维领域的研究中有广泛体现。R1模型的情况也是如此，但R1模型中的关系未在所选研究中得到广泛的实证检验。本节将进一步阐述其余模型中计算思维各领域间的关系。

R2.一些研究将所提出的干预措施的成功归因于应用的策略。格罗佛等人特别强调了其策略的教学设计，最终促进了学生理解计算思维概念（算法结构） [11]。雷佩宁等人还发现，涉及游戏设计、模拟和脚手架的可扩展游戏设计策略提升了学生的计算思维技能，突出了教学法在设计策略中的重要作用[69]。赛斯·洛佩兹、罗曼·冈萨雷斯和巴斯克斯·卡诺则采用了一种积极的教学方法，结论是参加研究的小学生在计算思维概念、逻辑和实践方面提高了自身的计算思维水平[93]。此外，还有一些研究结果支持这样一种假设，即游戏设计、利用软件敏捷方法促进的项目学习和建模与模拟等学习策略能够促进计算思维习得[9][51][52]。

R3.研究还讨论了学习策略在人口统计学因素（如性别、社会经济背景）带来的挑战中的作用，如在计算机科学方面表现不佳和学习动机不强[16][68]。研究认为，计算思维教学能激励学习者，尤其是女性和代表性不足的学生。更具体地说，雷佩宁等人[69]和约阿尼杜、贝内特等人[94]认为，可扩展的游戏设计学习策略有助于扩大计算机科学的参与范围。在参与可扩展游戏设计项目的4000多名学生中，56%是少数民族学生，45%是女生，女生中64%的人有兴趣继续参加计算思维活动。此外，少数民族因素并不影响学生继续参与计算思维的兴趣[69]。参与以色列等人研究的教师通过协作解决问题、建模、给予明确指导、同伴协作和引导发现来教授计算思维，以便贫困生和残疾学生能够学习计算机科学[92]。

R4.学习策略由工具支持。在32项以学生为中心的实证研究中，有21项利用工具来支持学习策略，帮助学生了解计算思维。各工具各有特点，可以用于支持不同的学习策略。例如，CTSiM等包括建模环境的工具可支持涉及建模的策略[76][82]。在所选研究中，游戏设计策略通常由Scratch等工具支持[95]，该工具能够让所有年龄的学生通过其营造的低阶环境体验游戏开发过程。

此外，有证据表明，在没有学习策略的情况下使用工具是无法习得计算思维知识的。登纳等人分析了108款由中学生在Creator中创作的游戏，发现这些游戏缺乏代码组织、程序文件和可用性设计[7]。他们认为，这是因为学生在设计游戏和理解一些编程概念方面面临困难，因此，他们建议，适当的指导对激发学生的学习动机至关重要。布伦南和雷斯尼克指出，利用Scratch开发项目的学生尽管已经集成一些编程结构，但有时仍无法解释自己的程序[6]。赵和舒特通过学生开发的游戏环境检测其计算思维的发展，指出学生计算思维水平的提高很大程度上可归因于对环境熟悉程度的提高[96]。

R5.也有证据表明，工具可以提高代表性不足的学生对编程和计算机科学的参与度。在一项研究中，小学女生在参加计算思维课程并在应用程序Inventor中设计游戏后，对软件教育的负面态度有所下降[71]。

此外，一些研究强调，某些工具的功能（如可视化界面）消除了与编程本质相关的挑战（如学习复杂编程语法的困难）[4][9][24][76][97]。

六、研究讨论

对知识库领域的分析表明，近年来，为确定计算思维的可测量要素，研究人员使用各种术语来描述计算思维要素的分类，如概念、实践、技能、态度、观点。这些术语通常有不同的含义。此外，框架提出的几个计算思维要素似乎也有多种分类方式。例如，抽象分别被归为运用“抽象思考能力”的思维过程[34]，“决定保留和忽略关于实体/对象的哪些信息的技能” [15]，以及抽象和模块化的实践，即“通过将较小部分的集合放在一起构建较大的事物” [6]。

在分析所選研究的过程中，我们记录了60多种不同的计算思维要素，这些要素有的由框架和定义提出，有的仅经过实证研究的评估。其中一些要素没有包括在定义框架中，这一点可以用计算思维领域的演变来解释。随着计算思维领域研究的进展，除了各个框架提出的要素外，实证研究在其评估中引入了更多的计算思维要素。其中一些要素在综述的研究中大量出现，这是因为其他研究采用的评估方法[12][48-55]。

许多回顾的实证研究将计算思维视为一种技能，例如温在介绍计算思维时将其定义为一种技能和态度，而该定义被广为接受[2]。此外，术语“计算思维技能”一词来源于安杰利等人、美国计算机科学教师协会和美国国际教育技术协会的定义和框架[15][33]。布伦南和雷斯尼克描述的编程结构或计算思维概念也经常受到评估。这一发现与张和努里提出的结果一致[36]。这可能是因为计算思维概念可以通过直接评估方法进行评估，此外，其中一些方法还具备自动化的优点，能给评估过程带来便利。相反，观点和态度很难通过直接评估方法考察，这很可能导致观点和态度的评估在综述的研究中出现的频率较低。

计算思维评估的有关方法主要包括通过前测/后测、自我报告和工件分析对计算思维进行评估。为全面了解学习过程，一些研究在评估的同时还进行了观察。尽管研究人员在努力开发通用的评估方法，但计算思维评估方法的选取很大程度上取决于每项研究的具体内容。这些评估方法大多是间接评估计算思维的自我报告法，提出了定义模型中不存在的计算思维要素。因此，我们可以得出这样的结论：学界在评估计算思维的内容和方法问题上尚未达成一致意见。这一结论与几项强调计算思维评估所面临挑战的研究一致[6][8-13][65]。

研究还表明，最常见的学习策略是基于游戏的相关策略以及利用脚手架和协作策略进行建模与模拟的相关策略。基于游戏设计的相关策略提高了学生的动机水平，而建模和模拟相关策略促进了计算思维的核心过程（如抽象和评估）。有证据表明，能够促进学生计算思维学习的学习策略至关重要，因为向年轻学生介绍计算思维而不采取适当的学习策略会导致学生难以习得计算思维。

综述研究中的工具提供了相关编程环境和社群，让学生参与到编程建构和实践中。其中大多数工具都具备可视化编程的特征。Scratch是最常用的工具，通常用于游戏和媒体设计。这可能要归因于以下几点：第一，Scratch的设计者提议将其作为支持计算思维开发的工具[95]；第二，在布伦南和雷斯尼克的框架中，计算思维要素是根据Scratch定义的，便于研究人员在其研究中使用Scratch[6]；第三，在Scratch中开发的项目可以运用Scratch等自动评估方法对计算思维进行评估[12]。

有几项研究探讨了计算思维相关因素，包括认知因素、非认知因素和人口因素。确定这些因素与计算思维的关系后，就可以根据这些因素为每种具体情况指出最合适的方法。大多数研究考察了性别和社会经济因素以及由此产生的挑战（如学生代表性不足、性别差异和社会差异）。对所选研究的回顾表明，虽然一些因素可能会影响计算思维的发展，但计算思维教学可以解决计算机科学参与度低的问题，并能提高代表性不足学生的兴趣。布伊特拉戈·弗洛·雷斯等人[20]讨论了由于编程的性质产生的可能影响计算思维习得的挑战，所选研究中的学者和教师对此并不特别关注，这可能是因为这些困难可以用工具解决。

能力建设在2015年后受到广泛关注。教师教育、专业发展和教师教授计算思维所需的知识是本文所选研究讨论的主要问题。其中很多研究主要讨论了教师面临的挑战，其他研究则提出了框架或讨论了专业发展和教师教育的干预措施。

研究提出的CTPK-12概念模型旨在为理解领域和交流领域的细节提供帮助，并记录K-12教育通过编程培养计算思维的信息，以供未来研究参考。CTPK-12概念模型可以扩展到包括高等教育或编程以外的其他方法（如动觉方法）。因此，随着计算思维领域的发展，CTPK-12概念模型纳入计算思维领域或子领域可能会成为未来研究的基础。

此外，CTPK-12模型可以作为提出假设研究模型的基础，在理论和统计估计之间建立直接联系。如图7所示，在该模型的部分计算思维领域之间提出研究假设，包括H1（学习策略领域和知识库领域之间）：游戏设计能够帮助人们习得计算思维技能；H2（学习策略领域和因素领域之间）：游戏设计可以激励女性学生，解决性别差异问题；H3（工具领域和学习策略领域之间）：Scratch提供了体验游戏开发的机会，支持游戏设计；H4（工具领域和因素领域之间）：Scratch可以激励女性学生，解决性别差异问题；H5（因素领域和知识库领域之间）：女性和男性学生习得的计算思维技能水平不同。

我们建议使用CTPK-12概念模型设计实证干预措施，旨在通过K-12教育中的编程训练教授和学习计算思维，以尽可能多地研究计算思维领域。此外，我们认为，实证研究应明确定义计算思维知识库的目标要素、应用的学习策略、使用的评估方法、使用的工具、参与者自身可能影响计算思维水平的因素及相关教师的能力建设，这样有利于全面了解正在试验的干预措施。

此外，CTPK-12概念模型可以与计算思维活动的模型相结合，例如自主范围模型 [80]和建构主义矩阵[98]。CTPK-12模型可用于指导设计教师课程，通过K-12教育中的编程训练，为教师提供实证结果和关于计算思维的详细信息，并帮助教师将计算思维融入教学实践中。在课程设计及计算思维教学过程中，可以考虑模型涉及的领域和这些领域之间的关系，以提高有效性。此外，CTPK-12模型也可以为决策者提供有关计算思维和融入K-12教育的决策信息。值得注意的是，在实际应用CTPK-12模型时，应考虑到模型将被纳入的环境，这些环境包括一些参数，如课程类型（选修或必修），或计算思维是与课程体系中的其他学科结合，还是作为一门单独课程。对这些环境的进一步阐述超出了本研究的范围。

七、研究结论和未来研究方向

本研究开发了一个在K-12教育中通过编程培养计算思维的概念模型（CTPK-12）。该模型以系统的文献综述和对计算思维领域及其关系的确定为基础。正如在科学出版物中所讨论的那样，计算思维領域源于研究者感兴趣的所有主题的记录。CTPK-12模型提供了计算思维领域的总体导图，有助于对计算思维领域的理解，并可作为未来研究的基础，促进计算思维与K-12教育实践的结合。

CTPK-12模型表明，在K-12教育领域中通过编程进行的计算思维训练包括以下6个相互关联的领域：知识库、学习策略、评估、工具、因素和能力建设领域。这些领域之间的一些关系还没有得到充分探讨，包括：第一，哪些工具支持哪些学习策略；第二，哪些学习策略能够帮助习得计算思维；第三，哪些因素影响计算思维的发展；第四，能力建设如何影响学生的计算思维水平。

CTPK-12模型还显示，尽管学界对评估、工具和因素领域的关注度随着时间的推移大致保持不变，但对学习策略和能力建设领域的关注度有所增加，而对知识库领域的关注度有所减少。这表明研究重点发生了变化，即转向更具体的教育实践问题。研究结果还指出了关于模型中各计算思维领域及其关系方面的差距和未来的研究方向。

根据所选研究，评估领域处于计算思维研究的前沿，是研究人员最感兴趣的领域。然而，所选研究中的计算思维评估方法主要包括基于特定活动和课程的方法，因此在不同环境下使用上述方法存在困难。研究人员已在努力开发通用的经过验证的方法，以便能够根据有效的研究工具来记录他们的研究结果。这些方法大多是自我报告法，因此，需要使用额外的、经过验证且可适用于各种环境的方法，使基于除自我报告法以外的其他计算思维评估方法标准化。

工具领域也是所选研究关注的主要主题之一。一些研究的重点是开发专门用于支持计算思维教学和学习策略的环境。这些环境虽然是在计算思维框架的基础上设计的，但未被广泛用于旨在开发计算思维的实证研究或教育实践中。相反，这些环境只在介绍它们的研究文献中出现过一次。因此，除计算思维工具的理论基础和技术特性外，研究人员还需要考虑可用性、学生动机、通过可用资源和框架为教师提供的便利，以及通过内置自动评估方法进行评估的便利性等问题。此外，未来的研究应探索工具和计算思维发展之间的关系，提供关于哪些工具可以更好地支持哪些计算思维学习策略的见解。

近年来，学习策略领域受到越来越多的关注。但是，一些选定的研究仅仅提到了应用的学习策略，并未进一步描述学习策略的实施方法。关注学习策略、介绍相关的背景以及如何实施学习策略，有助于更全面地了解所提出的计算思维干预措施的条件和背景。研究还可以提出支持利用计算思维学习策略的框架。此外，未来的研究可以探索学习策略和计算思维发展之间的关系，并就哪些学习策略最适合学生获得哪些计算思维要素提供见解。

能力建设是教育环境中计算思维的一个关键领域，也是计算思维研究中的一个新兴领域。尽管如此，诸多研究仍然认为，教师在将计算思维纳入教学实践方面面临重大挑战，如缺乏技术基础设施、缺乏时间制订课程计划和准备材料、教学时间有限[41][87][92][99][100]。最重要的是，教师的计算思维内容知识水平较低且缺乏如何教授计算思维知识的经验[15][79][88][89][92][101]。因此，需要更多的能力建设干预措施和框架来支持在职和职前教师将计算思维纳入他们的教学实践。此外，能力建设和计算思维发展之间的关系可以在未来的研究中进一步探讨。

选定的研究中有一些也对因素领域进行了考察。然而，一些研究结果是相互矛盾的，因此尚不清楚这些因素是否以及在何种程度上导致更高或更低的计算思维水平。正如安杰利和吉安纳科斯所指出的，关于计算思维技能（如抽象、问题分解和数据结构）如何映射不同的能力、年级、学科、性别和受教育程度，文献中仍缺少相关内容[102]。在这个方向上进一步研究可以明确可能影响计算思维习得的因素。关于如何利用计算思维激励代表性不足的群体，很少有研究专门针对激励女孩和代表性不足的少数民族[71][103][104]。因此，需要更多的研究证明因素、学习策略和工具之间的关系，并就学习策略和工具是否以及如何擴大参与计算思维和解决与因素相关的挑战提供见解。

最后，未来的研究工作可以充分探索CTPK-12模型在教育实践和研究中的潜在用途，例如对该模型在教学实践和课程设计中的应用进行研究。此外，未来研究工作可以将该模型的应用扩展到高等教育，以开发一种全面的方法，涵盖从幼儿期到研究生的计算思维教学和学习。

【参考文献】

[1] PAPERT S. Mindstorms： Children， Computers， and Powerful Ideas[M]. New York： Basic Books， 1980.

[2] WING J M. Computational thinking[J]. Communications of the ACM， 2006， 49（03）： 33-35.

[3] GROVER S， PEA R. Computational thinking in K-12： A review of the state of the field[J]. Educational Researcher， 2013， 42： 38-43.

[4] LYE S Y， KOH J H L. Review on teaching and learning of computational thinking through programming： What is next for K-12？ [J].Computers in Human Behavior， 2014， 41： 51-61.

[5] HSU TC， CHANG SC， HUNG YT. How to learn and how to teach computational thinking： Suggestions based on a review of the literature[J]. Computers and Education， 2018， 126： 296-310.

[6] BRENNAN K， RESNICK M. New frameworks for studying and assessing the development of computational thinking[C]//American Educational Research Association. Proceedings of the 2012 Annual Meeting of the American Educational Research Association （AERA）， 2012： 1-25.

[7] DENNER J， WERNER L， ORTIZ E. Computer games created by middle school girls： Can they be used to measure understanding of computer science concepts？[J] Computers and Education， 2012， 58（01）： 240-249.

[8] DENNING P J. Remaining trouble spots with computational thinking[J]. Communications of the ACM， 2017， 60（06）： 33-39.

[9] FRONZA I， EL IOINI N， CORRAL L. Teaching computational thinking using agile software engineering methods： A framework for middle schools[J]. ACM Transactions on Computing Education， 2017， 17（04）：1-28.

[10] GROVER S， BASU S， BIENKOWSKI M， et al. A framework for using hypothesis-driven approaches to support data-driven learning analytics in measuring computational thinking in block-based programming environments[J]. ACM Transactions on Computing Education， 2017， 17（03）：1-25.

[11] GROVER S， PEA R， COOPER S. Designing for deeper learning in a blended computer science course for middle school students[J]. Computer Science Education， 2015， 25（02）： 199-237.

[12] MORENO LEÓN J， ROBLES G， ROMÁN GONZÁLEZ M. DR. Scratch： Automatic analysis of Scratch projects to assess and foster computational thinking[J]. RED： Revista de Educación a Distancia， 2015 （46）： 1-23.

[13] ZHONG B， WANG Q， CHEN J， et al. An exploration of three-dimensional integrated assessment for computational thinking[J]. Journal of Educational Computing Research， 2016， 53（04）： 562-590.

[14] DOLGOPOLOVAS V， DAGIENEĖ V， JASUTĖ E， et al. Design science research for computational thinking in constructionist education： A pragmatist perspective[J]. Problemos， 2019， 95： 144-159.

[15] ANGELI C， VOOGT J， FLUCK A， et al. A K-6 computational thinking curriculum framework： Implications for teacher knowledge[J]. Educational Technology and Society， 2016， 19（03）： 47-57.

[16] COOPER S， GROVER S， GUZDIAL M， et al. Education： A future for computing education research[J]. Communications of the ACM， 2014， 57（11）： 34-36.

[17] YADAV A， STEPHENSON C， HONG H. Computational thinking for teacher education[J]. Communications of the ACM， 2017， 60（04）： 55-62.

[18] SHUTE V J， SUN C， ASBELL-CLARKE J. Demystifying computational thinking[J]. Educational Research Review， 2017， 22： 142-158.

[19] KALELIOGLU F， GULBAHAR Y， KUKUL V. A framework for computational thinking based on a systematic research review[J]. Baltic Journal of Modern Computing， 2016， 4（03）： 583-596.

[20] BUITRAGO FLÓREZ F， CASALLAS R， HERNÁNDEZ M， et al. Changing a generation’s way of thinking： Teaching computational thinking through programming[J]. Review of Educational Research， 2017， 87： 834-860.

[21] HSU YC， IRIE N R， CHING YH. Computational thinking educational policy initiatives （CTEPI） across the globe[J]. TechTrends， 2019，63：260-270.

[22] PASSEY D. Computer science （CS） in the compulsory education curriculum： Implications for future research[J]. Education and Information Technologies， 2017， 22（02）： 421-443.

[23] CSIZMADIA A， CURZON P， DORLING M， et al. Computational thinking： A guide for teachers[EB/OL].（2015）. https：//community.computingatschool. org.uk/resources/2324/single

[24] GARCÍA-PEÑALVO F J， MENDES A J. Exploring the computational thinking effects in pre-university education[J]. Computers in Human Behavior， 2018， 80： 407-411.

[25] MYLOPOULOS J. Conceptual modelling and telos[M]//Loucopoulos P， Zicari R. Conceptual Modeling， Databases， and Case an Integrated View of Information Systems Development. New York： Wiley， 1992： 49-68.

[26] GEMINO A， WAND Y. A framework for empirical evaluation of conceptual modeling techniques[J]. Requirements Engineering， 2004， 9（04）： 248-260.

[27] WEBSTER J， WATSON R. Analyzing the past to prepare for the future： Writing a literature review[J]. MIS Quarterly， 2002， 26（02）： 13-23.

[28] WAND Y， WEBER R. Research commentary： Information systems and conceptual modeling-a research agenda[J]. Information Systems Research， 2002， 13（04）： 363-376.

[29] WING J M. Computational thinking and thinking about computing[J]. Philosophical Transactions of the Royal Society A： Mathematical， Physical and Engineering Sciences， 2008， 366（1881）： 3717-3725.

[30] AHO A V. Computation and computational thinking[J]. Computer Journal， 2012，55（07）： 832-835.

[31] ROMÁN-GONZÁLEZ M， PÉREZ-GONZÁLEZ J-C， JIMÉNEZ-FERNÁNDEZ C. Which cognitive abilities underlie computational thinking？ Criterion validity of the computational thinking test[J]. Computers in Human Behavior， 2017， 72： 678-691.

[32] BARR V， STEPHENSON C. Bringing computational thinking to K-12： What is involved and what is the role of the computer science education community？[J]. ACM Inroads， 2011， 2（01）： 48-54.

[33] CSTA & ISTE. Operational definition of computational thinking[EB/OL]. （2011）. https：//www.iste.org/explore/Solutions/Computational- thinking-for-all.

[34] SELBY C. Computational thinking： The developing definition[C]//SIGCSE. ITiCSE Conference， 2013： 5-8.

[35] WEINTROP D， BEHESHTI E， HORN M， et al. Defining computational thinking for mathematics and science classrooms[J]. Journal of Science Education and Technology， 2016， 25： 127-147.

[36] ZHANG L C， NOURI J. A systematic review of learning computational thinking through Scratch in K-9[J]. Computers and Education， 2019， 141（June）： 103607.

[37] VOOGT J， FISSER P， GOOD J， et al. Computational thinking in compulsory education： Towards an agenda for research and practice[J]. Education and Information Technologies， 2015， 20（04）： 715-728.

[38] BASOGAIN X， OLABE M Á， OLABE J C， et al. Computational thinking in pre-university blended learning classrooms[J]. Computers in Human Behavior， 2018， 80： 412-419.

[39] KAFAI Y B. From computational thinking to computational participation in K-12 education[J]. Communications of the ACM， 2016， 59： 26-27.

[40] HEINTZ F， MANNILA L， FARNQVIST T. A review of models for introducing computational thinking， computer science and computing in K-12 education [C]//IEEE. Proceedings - Frontiers in Education Conference （FIE）， 2016.

[41] BARGURY I Z， HABERMAN B， COHEN A， et al. Implementing a new computer science curriculum for middle school in Israel[C]//IEEE. Proceedings - Frontiers in Education Conference （FIE）， 2012.

[42] CHING Y-H， HSU Y-C， BALDWIN S. Developing computational thinking with educational technologies for young learners[J]. TechTrends， 2018， 62： 563-573.

[43] DA CRUZ ALVES N， GRESSE VON WANGENHEIM C， HAUCK J C R. Approaches to assess computational thinking competences based on code analysis in K-12 education： A systematic mapping study[J]. Informatics in Education， 2019， 18： 17-39.

[44] MOHER D， LIBERATI A， TETZLAFF J， et al. Preferred reporting items for systematic reviews and meta-analyses： The PRISMA Statement[J]. BMJ， 2009， 339 （7716）： 332-336.

[45] HSIEH H F， SHANNON S E. Three approaches to qualitative content analysis[J]. Qualitative Health Research， 2005， 15（09）： 1277-1288.

[46] SIAU K， TAN X. Improving the quality of conceptual modeling using cognitive mapping techniques[J]. Data & Knowledge Engineering， 2005， 55（03）： 343-365.

[47] VON WANGENHEIM C G， HAUCK J C R， DEMETRIO M F， et al. CodeMaster - Automatic assessment and grading of app inventor and snap！ Programs[J]. Informatics in Education， 2018， 17（01）： 117-150.

[48] KORKMAZ Ö， ÇAKIR R， ÖZDEN M Y. A validity and reliability study of the computational thinking scales （CTS）[J]. Computers in Human Behavior， 2017， 72（JUL.）： 558-569.

[49] DURAK H Y， YILMAZ F G K， BARTIN R Y. Computational thinking， programming self-efficacy， problem solving and experiences in the programming process conducted with robotic activities[J]. Contemporary Educational Technology， 2019， 10（02）： 173-197.

[50] GABRIELE L， BERTACCHINI F， TAVERNISE A， et al. Lesson planning by computational thinking skills in Italian pre-service teachers[J]. Informatics in Education， 2019， 18： 69-104.

[51] GARNELI V， CHORIANOPOULOS K. Programming video games and simulations in science education： exploring computational thinking through code analysis[J]. Interactive Learning Environments， 2018， 26： 386-401.

[52] GARNELI V， CHORIANOPOULOS K. The effects of video game making within science content on student computational thinking skills and performance[J]. Interactive Technology and Smart Education， 2019，16（04）： 301-318.

[53] GÜNBATAR M S. Computational thinking within the context of professional life： Change in CT skill from the viewpoint of teachers[J]. Education and Information Technologies， 2019， 24： 2629-2652.

[54] KORKMAZ Ö， BAI X. Adapting computational thinking scale （CTS） for Chinese high school students and their thinking scale skills level[J]. Participatory Educational Research， 2019， 6（01）： 10-26.

[55] MARCELINO M J， PESSOA T， VIEIRA C， et al. Learning computational thinking and scratch at distance[J]. Computers in Human Behavior， 2018， 80： 470-477.

[56] CHEN G， SHEN J， BARTH-COHEN L， et al. Assessing elementary students’ computational thinking in everyday reasoning and robotics programming[J]. Computers and Education， 2017， 109： 162-175.

[57] KONG S-C， CHIU M M， LAI M. A study of primary school students’ interest， collaboration attitude， and programming empowerment in computational thinking education[J]. Computers and Education， 2018， 127： 178-189.

[58] KUKUL V， KARATAS S. Computational thinking self-efficacy scale： Development， validity and reliability[J]. Informatics in Education， 2019， 18： 151-164.

[59] YAĞCı M. A valid and reliable tool for examining computational thinking skills[J]. Education and Information Technologies， 2019， 24（01）： 929-951.

[60] DE SOUZA A A， BARCELOS T S， MUNOZ R， et al. Data mining framework to analyze the evolution of computational thinking skills in game building workshops[J]. IEEE Access， 2019， 7： 82848-82866.

[61] SNOW E， RUTSTEIN D， BASU S， et al. Leveraging evidence-centered design to develop assessments of computational thinking practices[J]. International Journal of Testing， 2019， 19： 103-127.

[62] PIAGET J. Genetic Epistemology[M]. New York： Columbia University Press， 1970.

[63] VYGOTSKY L S. Mind in Society： The Development of Higher Psychological Processes[M]. Harvard University Press， 1978.

[64] ATMATZIDOU S， DEMETRIADIS S. Advancing students’ computational thinking skills through educational robotics： A study on age and gender relevant differences[J]. Robotics and Autonomous Systems， 2016， 75： 661-670.

[65] WERNER L， DENNER J， CAMPE S， et al. The fairy performance assessment： Measuring computational thinking in middle school[C]//SIGCSE. SIGCSE’ 12- Proceedings of the 43rd ACM Technical Symposium on Computer Science Education， 2012： 215-220.

[66] DURAK H Y， SARITEPECI M. Analysis of the relation between computational thinking skills and various variables with the structural equation model[J]. Computers and Education， 2018， 116： 191-202.

[67] ISRAEL-FISHELSON R， HERSHKOVITZ A. Persistence in a game-based learning environment： The case of elementary school students learning computational thinking[J]. Journal of Educational Computing Research， 2019，58（05）： 891-918.

[68] FLETCHER G H L， LU J J. Education： Human computing skills： Rethinking the K-12 experience[J]. Communications of the ACM， 2009， 52（02）： 23-25.

[69] REPENNING A， GROVER R， GUTIERREZ K， et al. Scalable game design[J]. ACM Transactions on Computing Education， 2015， 15（02）： 1-31.

[70] ALLSOP Y. Assessing computational thinking process using a multiple evaluation approach[J]. International Journal of Child-Computer Interaction， 2019， 19： 30-55.

[71] KIM Y-M， KIM J-H. Application of a software education program developed to improve computational thinking in elementary school girls[J]. Indian Journal of Science and Technology， 2016， 9.

[72] NOURI J， ZHANG L， MANNILA L， et al. Development of computational thinking， digital competence and 21st century skills when learning programming in K-9[J]. Education Inquiry， 2020， 11（01）： 1-17.

[73] HERSHKOVITZ A， SITMAN R， ISRAEL-FISHELSON R， et al. Creativity in the acquisition of computational thinking[J]. Interactive Learning Environments， 2019， 27： 628-644.

[74] ROMÁN-GONZÁLEZ M， PÉREZ-GONZÁLEZ J C， MORENO-LEÓN J， et al. Extending the nomological network of computational thinking with non-cognitive factors[J]. Computers in Human Behavior， 2018， 80（MAR.）： 441-459.

[75] WITHERSPOON E B， SCHUNN C D. Teachers’ goals predict computational thinking gains in robotics[J]. Information and Learning Science， 2019， 120： 308-326.

[76] SENGUPTA P， KINNEBREW J S， BASU S， et al. Integrating computational thinking with K-12 science education using agent-based computation： A theoretical framework[J]. Education and Information Technologies， 2013， 18： 351-380.

[77] CLARK D B， SENGUPTA P. Reconceptualizing games for integrating computational thinking and science as practice： collaborative agent-based disciplinarily-integrated games[J]. Interactive Learning Environments， 2020， 28（03）： 328-346.

[78] XING W. Large-scale path modeling of remixing to computational thinking[J]. Interactive Learning Environments， 2021， 29（03）：414-427.

[79] CHALMERS C. Robotics and computational thinking in primary school[J]. International Journal of Child-Computer Interaction， 2018， 17： 93-100.

[80] CARLBORG N， TYRÉN M， HEATH C， et al. The scope of autonomy when teaching computational thinking in primary school[J]. International Journal of Child-Computer Interaction， 2019， 21： 130-139.

[81] WEINTROP D， HOLBERT N， HORN M S， et al. Computational thinking in constructionist video games[J]. International Journal of Game-Based Learning， 2016， 6（01）： 1-17.

[82] BASU S， BISWAS G， KINNEBREW J S. Learner modeling for adaptive scaffolding in a computational thinking-based science learning environment[J]. User Modeling and User-Adapted Interaction， 2017， 27（01）： 1-49.

[83] KYNIGOS C， GRIZIOTI M. Programming approaches to computational thinking： Integrating turtle geometry， dynamic manipulation and 3D space[J]. Informatics in Education， 2018， 17： 321-340.

[84] MOUZA C， YANG H， PAN Y-C， et al. Resetting educational technology coursework for pre-service teachers： A computational thinking approach to the development of technological pedagogical content knowledge （TPACK）[J]. Australasian Journal of Educational Technology， 2017， 33： 61-76.

[85] KOEHLER M J， MISHRA P. Technological pedagogical content knowledge： A framework for teacher knowledge Punya Mishra[J]. Teachers College Record， 2006， 108（06）： 1017–1054.

[86] YADAV A， MAYFIELD C， ZHOU N， et al. Computational thinking in elementary and secondary teacher education[J]. ACM Transactions on Computing Education， 2014， 14（01）：1-16.

[87] ADLER R F， KIM H. Enhancing future K-8 teachers’ computational thinking skills through modeling and simulations[J]. Education and Information Technologies， 2018， 23： 1501-1514.

[88] ALFAYEZ A A， LAMBERT， J. Exploring Saudi computer science teachers’ conceptual mastery level of computational thinking skills[J]. Computers in the Schools， 2019， 36： 143-166.

[89] BOWER M， WOOD L N， LAI J W M， et al. Improving the computational thinking pedagogical capabilities of school teachers[J]. Australian Journal of Teacher Education， 2017， 42（03）： 53-72.

[90] HICKMOTT D， PRIETO-RODRIGUEZ E. To assess or not to assess： Tensions negotiated in six years of teaching teachers about computational thinking[J]. Informatics in Education， 2018， 17： 229-244.

[91] KALE U， AKCAOGLU M， CULLEN T， et al. Contextual factors influencing access to teaching computational thinking[J]. Computers in the Schools， 2018， 35： 69-87.

[92] ISRAEL M， PEARSON J N， TAPIA T， et al. Supporting all learners in school-wide computational thinking： A cross-case qualitative analysis[J]. Computers and Education， 2015， 82： 263-279.

[93] SÁEZ-LÓPEZ J M， ROMÁN-GONZÁLEZ M， VÁZQUEZ-CANO E. Visual programming languages integrated across the curriculum in elementary school： A two-year case study using “scratch” in five schools[J]. Computers and Education， 2016， 97： 129-141.

[94] IOANNIDOU A， BENNETT V， REPENNING A， et al. Computational thinking patterns[C]//American Educational Research Association. Proceedings of the 2011 Annual Meeting of the American Educational Research Association （AERA）， 2011.

[95] RESNICK M， MALONEY J， MONROY-HERNÁNDEZ A， et al. Scratch： Programming for all[J]. Communications of the ACM， 2009， 52（11）： 60-67.

[96] ZHAO W， SHUTE V J. Can playing a video game foster computational thinking skills？ [J]. Computers and Education， 2019， 141（July）： 103633.

[97] REPENNING A， BASAWAPATNA A R， ESCHERLE N A. Emerging Research， Practice， and Policy on Computational Thinking[J]. Emerging Research， Practice， and Policy on Computational Thinking， 2017： 291-305.

[98] CSIZMADIA A， STANDL B， WAITE J. Integrating the constructionist learning theory with computational thinking classroom activities[J]. Informatics in Education， 2019， 18： 41-67.

[99] OZTURK Z， DOOLEY C M M， WELCH M. Finding the hook： Computer science education in elementary contexts[J]. Journal of Research on Technology in Education， 2018， 50（02）： 149-163.

[100] SENTANCE S， CSIZMADIA A. Computing in the curriculum： Challenges and strategies from a teacher’s perspective[J]. Education and Information Technologies， 2017， 22（02）： 469-495.

[101] KALE U， AKCAOGLU M， CULLEN T， et al. Computational what？ Relating computational thinking to teaching[J]. TechTrends， 2018， 62： 574-584.

[102] ANGELI C， GIANNAKOS M. Computational thinking education： Issues and challenges[J]. Computers in Human Behavior， 2020， 105：106185.

[103] LEONARD J， MITCHELL M， BARNES-JOHNSON J， et al. Preparing teachers to engage rural students in computational thinking through robotics， game design， and culturally responsive teaching[J]. Journal of Teacher Education， 2018， 69： 386-407.

[104] PINKARD N， MARTIN C K， ERETE， S. Equitable approaches： opportunities for computational thinking with emphasis on creative production and connections to community[J]. Interactive Learning Environments， 2019（06）： 1-15.

Abstract： Computational Thinking （CT） through programming attracts increased attention as it is considered an ideal medium for the development of 21st century skills. This intense attention leads to K-12 initiatives around the world and a rapid increase in relevant research studies. However， studies show challenges in CT research and educational practice. In addition， the domain has not been mapped to facilitate comprehensive understanding of the domain challenges and development of CT curricula. The purpose of this study is to develop a conceptual model based on a systematic literature review that maps the CT through programming in K-12 education domain. The proposed Computational Thinking through Programming in K-12 education （CTPK-12） conceptual model emerges from the synthesis of 101 studies and the identification of CT Areas. The proposed model consists of six CT Areas （namely Knowledge Base， Learning Strategies， Assessment， Tools， Factors and Capacity Building） and their relationships. The model could aid domain understanding and serve as a basis for future research studies. In addition， it could support the integration of CT into K-12 educational practices， providing evidence to educational stakeholders and researchers as well as bringing closer research， practice and policy.

Keywords： Computational Thinking; Programming; K-12 Education

（責任编辑：邱天敏）