国外中小学代数推理研究的主要成果及其启示

谢春艳 黄娜娜 潘禹辰 徐文彬

【摘 要】 支持代数推理能力发展的基础性与连贯性，是国外中小学代数推理研究的基本特征.具体而言，其代数推理研究从算术与代数、算术思维与代数思维的区别与联系出发，提出“早期代数”的可行性，继而从代数推理的认知分析与发展策略两个方面展开深入研究，呈现出理论与实践互相补充的大致发展趋势.由此，我国中小学代数推理研究应该提高对概念理解的重视程度，考虑代数推理任务的连贯性，促进教师专业发展，以改善算术与代数教学割裂的现实状况.

【关键词】 代数推理；代数思维；认知分析；发展策略

代数在不同国家的现行中小学数学课程中基本都处于核心地位，而真正关注到（低年级）代数教学的重要性是在2000年之后.代数作为一种解决问题的工具，为分析数量之间的关系、建立模型以及说明和证明提供了一般化的语言和结构，而代数思维中代数推理能力的培养是代数教学的核心问题.国外代数推理研究要早于国内，研究成果也较为成熟.本研究试总结国外代数推理研究的主要成果，并为国内相关研究的开展提出若干启示.

1 研究概貌

在“Web of Science”中以“Algebraic Reasoning”为标题进行检索，数据库选择SCI-Expanded、SSCI、CPCI-S和CPCI-SSH，截至2022年8月，共检索到77篇文献，经筛选得到相关性较高的文献16篇.同时在“ERIC”中以“Algebraic Reasoning”为主题词进行检索，共检索到419篇文献，经阅读排除无关或低相关文献，得到文献74篇.在相关中文文献阅读过程中补充了12篇外文文献，最终以102篇代数推理研究文献作为分析对象，其中，期刊论文64篇，会议论文30篇，研究报告8篇.

1.1 年度分布

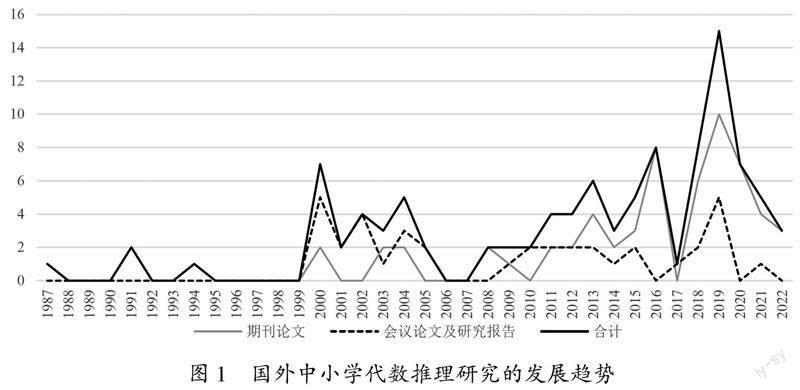
如图1所示，国外的中小学代数推理研究自2000年后表现出小幅波动的发展态势.期刊论文与会议论文数量相差不大，2010年之前以会议论文及研究报告居多，这类研究常出现在数学教育研究、数学教育心理学研究等国际会议上；2010年之后期刊论文数量逐步增加，会议论文数量基本持平，“代数推理”仍然是国际会议中关心的问题.与此同时，更多数学教育者对“代数推理”的数学教育实践展开行动干预，给出调查结论.

1.2 关键词分布

通过对文献关键词的统计分析（有些文献资料未写明关键词，则根据摘要与文章内容提取关键词），可将研究主要分为代数推理的理论研究、代数推理的认知分析以及代数推理的发展策略三个部分.代数推理的理论研究中，以对算术与代数的基本了解为基础，进一步区分算术思维与代数思维（算术推理与代数推理），并提出“早期代数”的想法.代数推理的认知分析中，可以将关键词归为认知内容、认知层次和认知困境三类.认知内容方面，“概念理解”“概念教学”“乘法思维”“方程”“代数表达式”等词出现频次较高，是学生代数推理思考的重要部分.认知层次方面，主要是“评估”类研究，相对较少.认知困境主要体现在问题解决中不同类型问题的设置，语言表达方式和知识类型对学生理解并完成代数任务的影响.代数推理的发展策略中，主要关注教师在代数推理教学中所发挥的关键作用，兼顾教师的教学观念、专业知识以及教学技能.

1.3 研究方法

教育研究主要包括理论研究、实证研究、实践研究三种方法.其中，理论研究又可分为演绎研究（先验推理论证）、归纳研究（经验推理论证）与类比研究；实证研究可分为历史研究、调查研究与实验研究，实证研究报告具有完整的问题假设、过程与方法、结果与讨论；实践研究主要表现为日常的教学经验总结和策略分析.

基于上述分类统计国外代数推理研究的研究方法，发现其以实证研究为主（82篇），其次是理论研究（16篇）和实践研究（4篇）.实证研究大多基于已有研究成果的基本观点进一步分析测试结果与访谈记录，其中以定性研究居多，因为代数推理相比算术推理更具动态性，需要对学生的概念理解、程序技能及问题解决展开连续的观察.另外，实验研究也是关注代数推理能力动态发展的重要研究方法，尤其在培养教师代数推理教学能力的过程中，研究往往通过课程干预的方式，发展教师的“教学敏感性”.

2 研究内容

根据前述对关键词分析所确定的三大研究内容，下面将作具体分析.

2.1 代数推理的理论研究

与国内研究从逻辑学角度出发理解代数推理不同，国外研究者多从代数意义进行理解，因此在探究代数推理的本质意义之前，对算术与代数的基本理解在研究中受到重视，而且由此可发现算术思维与代数思维的密切联系.

2.1.1 算术与代数的区别与联系

算术的基本对象是数，包括数的认识与数的运算等，而代数的基本对象除了数以外，还有更具广泛意义的符号，主要体现为数的关系.出于代数的本体意义和功能意义两种不同的视角，研究者对代数的理解有所不同（详见表1）.本体意义上，代数主要包括算术的一般化、关系、结构、函数、模型等；功能意义上，代数主要在概括描述、规则操作、问题解决程序中体现出特殊的代数思想和方法.以上虽有不同，但这些理解也体现出，从算术到代数的学习，表现为从具体到一般的运算，而且学生在代数学习过程中也更要懂得代数的符号化、形式化、结构化与操作化的特点.

要说清算术与代数的区别是相对较难的.从符号意义来看，算术与代数存在许多相同的符号，但意义却大相径庭，比如对“等号”的理解是计算结果还是等价关系、对“字符”的理解是传统的未知数还是任意一个数；从解题活动来看，算术是面向解決问题的答案，而非解决问题本身，代数的解题活动重在发现关系，操作代数规则[6]328.由此可知，儿童在算术中对“符号”“关系”“关系的转换”的理解，可能会影响代数学习，因为算术与代数是紧密联系的.两者的联系可以用数学概念的二重性理论解释.抽象数学符号必须基于两种不同的方法来思考，一是结构性（视为对象），二是操作性（视为过程），而算术与代数之间的联系，就需经历操作—结构（过程—对象）的转换，包括内化、压缩与客体化的过程，代数思维与代数推理体现其中[7]，需要将概念理解、程序技能和解决问题的能力融入学生的早期学习经验[8].

2.1.2 算术思维与代数思维的区别与联系

算术思维注重利用数量的计算得出结果，联结题目与答案，这个过程是程序性的、含情境的，具有特殊性、计算性的特点；而代数思维倚重的是关系的符号化及其运算，联结量与量之间的关系，这个运算是结构性的、去情境的，具有一般性、形式化的特点[6]327.在算术思维到代数思维的过渡中，两者可能基于同一套符号体系，是转换的基础，但是需意识到两者对符号的解释有所不同，对符号的使用也存在不同的操作，更涉及观念的转变.

具体而言，代数思维的特征主要包括五个方面.首先，代数思维的核心是一般化的思想.Kaput认为“代数是算术推理和定量推理的一般化，代数是一种句法导向的形式操作”是代数最关键的基本特征，代数思维体现一般化与形式化[2]4；Harel和Tall进一步指明代数的一般化主要有扩展性一般化、重构性一般化与分离性一般化三种类型[9].其次，代数思维是一种形式的符号操作，“成功地操作代数符号的能力要求我们首先能理解数学运算和关系的结构属性……代数表征和符号操作的本质特征是它应该来自于对语义或它所指意义的理解”[10].第三，代数思维是一种基于规则的推理，“代数是一种句法导向的形式操作，此种句法是指代数规则”[3]10.第四，代数思维是一种建模活动，在代数思维中可通过模式反映对象之间的某种规律，Berlin等人认为，从模式入手的课程能够提升学生的思考与理解能力，学生需要从实际情境中选取素材，转化为数学问题，再回到实际情境以评价结果，从而提升數学的真实感[11].最后，代数思维是多种推理能力的重要预测指标.有研究指出代数思维的多面性及其与认知能力的关系，除了类比和归纳等推理形式外，空间推理也是学生代数思维能力的重要预测指标[12].代数思维的以上五个特征，就一般思维的意义而言，学生将发展抽象概括、概念理解、理性分析、联系实践和推理能力的思考方法.

在目前的代数推理研究中，基本确定“代数推理是一个过程，学生通过这种过程来寻找某些数学问题或情境的模式，在数量之间建立关系，并通过形式化的象征表征和操纵来进行概括”[13].

2.2 代数推理的认知分析

基于对算术与代数、算术思维与代数思维的分析，许多研究者继而关注学生在代数推理方面的认知情况.实际上，教师不仅要提供数学材料，还应了解学生如何学习数学，即他们的认知过程（包括认知内容、认知层次、认知困境）[14]，所以关注这方面的研究很重要.

2.2.1 认知内容

在确定代数推理的认知内容时，研究者多关注学生的学习进程或轨迹，提出了代数的“大概念”以及相应的“核心概念”，并以此作为代数思维实践的教学任务序列.“大概念”主要有：等价、表达式、方程和不等式；广义算术；泛函思维；变量；比例推理[15].譬如，“乔治亚数学与科学行动”（Georgia Initiative in Mathematics and Science，简称GIMS），按照学段给出了代数的“Big Ideas”（大概念），每阶段代数推理学习的核心思想保持一致，本质上都是理解一般化、关系、结构，区别在于认知对象范围的扩大以及认知阶段目标的发展[6]310.结合其他研究来看，代数推理内容的学习主要以理解等价关系和乘法思维、发现乘法推理与加法推理的区别为主，这可能是因为等价关系是代数结构进行转化的依据，而乘法是理解其他运算规律的基本概念.熟悉以上代数课程的基本内容，可以更好地建立起小学与初中代数内容的联系，算术与代数并非完全割裂的两部分，如何在算术中教代数，体现了对代数思维及代数推理的关注.

一些研究者从代数推理能力的要求出发，结合完整的代数推理过程确定认知内容.Harper在调查研究中业已证实学生在代数学习时，对一些问题的回答依次对应每一阶段的代数方法，即“修辞代数——半符号代数——符号代数”[16].有研究者提出“战略代数推理”的概念，关注学生的战略能力及自适应推理，并提出五大能力的代数学习内容：阅读和解释文本，理解问题陈述中的故事情节（背景）；确定数量和它们之间的关系（识别数量、发现关系）；使用数量之间关系的代数表示（生成表示、解释表示）；精确执行计算和程序并检查结果的合理性；提供令人信服的解释[17].Sarah R. Powell在研究中概括了代数推理过程所涉及的三种不同活动：代表性的——学生将口头信息翻译成符号表达式和方程式，还努力理解数学概念、运算和关系的概念基础；变革性的——学生学习基于规则的活动，例如因式分解、扩展、替换、求解方程和简化表达式；概括和证明——学生学习解决问题、建模、注释结构、证明和预测[10]327.以上内容也基本概括了多数研究中代数推理测试或代数推理教学的过程，代数推理支持学生有机会掌握一种代数的方法来解决问题，在证明推理、使用多种表示的过程中识别结构和关系.

2.2.2 认知层次

大型测评项目中的研究者倾向于选择构建金字塔评价模型来测评代数推理的认知层次，譬如，美国国家数学科学教育研究中心开展的基于情境中的数学的评价项目（MIC）[19]，但是这类模型对代数的内容细化不够，不足以充分反映代数推理的特征.还有研究者使用SOLO模型，将代数学习的四个重要方面（一般特征、模式、表征、变量）与SOLO模型中的四个水平（前结构、单结构、多结构、关系）相结合，最终确定学生代数推理学习的具体表现，但是，同一个问题情境中往往不止体现代数学习的一个方面，代数推理能力的层次应该也体现在多个代数概念的联结水平中.此外，澳大利亚RMF Ⅱ项目根据Rasch分析创建的项目层次结构确定了八个区域来假设学生的学习进程，学生行为的描述源于对每个区域内项目的认知需求的考虑[20].这种方式既能细化代数内容，确定代数推理的核心概念，又能基于核心概念的学习进展给出每一阶段的层次水平，有助于学习者识别出自己在代数推理学习进程中的位置，并基于即时的学习体验，在下一步的学习中找到联系.

2.2.3 认知困境

研究者多通过问卷测试与访谈来分析并比较结果，从而发现导致学生在代数推理上存在差异的因素，进而判断其认知困境.从学生自身来说，年龄、性别以及认知风格等方面都是可能的影响因素，所以学生的学习模式应该有所不同[21].从代数问题的设置来说，问题的难易程度、问题的类型、未知数量在问题中的位置、问题的语言表达以及有趣的问题情境等都会影响代数推理的进行[22][3]169.解题过程还会受到知识迁移、计算技巧的掌握、问题的求解策略等方面的影响[23][24].究其根本，主要是学生对代数的抽象性和形式化不适应，不能熟练运用代数的符号表征系统和形式规则，数学符号的学习还存在口语挑战、阅读挑战及书写困难，需要在学习过程中激发学生的学习动机，体会符号表达的重要性[6]339.再者，需要注意的是学生在代数推理过程中，最困难的是对代数结构的理解.代数结构的出现，对习惯于完成具体化操作的大多数学生而言是比较陌生的，因为他们无法观察整体对象，如解方程时使用逆运算而非先观察到方程的整体平衡关系.

2.3 代数推理的发展策略

以上代数推理认知维度的分析，表明了发展代数推理需要遵循学科的发展规律、学生的认知规律以及教学规律，因此在发展代数推理的过程中，“早期代数”、教师专业发展、教学策略的提出可能有助于学生获得较好的代数推理学习效果.

2.3.1 “早期代数”

经过一定训练的学生要明显比没有提前渗透代数内容和思想的学生能更合理地进行推理，而在小学算术教学中有效渗透代數推理是“早期代数”研究的主要观点，并在相关研究项目中得以证实[25].在“早期代数”中渗透代数推理，美国研究者建议教师可以利用四则运算中的逆运算和重复运算，在小学课堂的算术推理中使用多种表征方式[26]；澳大利亚在小学阶段的计算教学中提到了一种“皮特的算法”，是指在计算“32-5”这一等式时，不是直接计算得出答案，而是使用像“32+5-10”这样的步骤来学习知识和培养推理能力[27]；新西兰通过“学生数字运算的代数性质”的研究，给出像“47+25=47+3+25-3=50+22”这样的算式例子，体现出学生对数字间一般化关系的理解，不依靠字母或符号也可以实现一般化的策略，这种方法也被表示为“准变量表达式”[28].不管是可逆性变换，还是借用多种语用表达或外部模型，都体现出教学支架的作用，可以帮助学生降低代数推理的学习难度.

2.3.2 教师专业发展

国外研究非常重视教师在代数教学过程中的影响，认为教师应改变对代数的看法和教学方式，并关注学生对学习的看法[29].因此，代数推理的教学应该关注学生、教师与课程的整体联系.基于Bair和Rich构建的数学教学知识框架[30]，对职前或在职教师的代数推理教学能力分析中，都会从教学内容知识与学科关键知识出发进行专业发展干预，教师在代数推理教学实践中，需要经历“对代数概念的认识与关注——制定修改任务——开发课堂实践提供推理机会——开发数学实践支持代数推理”四个阶段[31].除了对代数推理教学提出要求，多数研究中提及元认知指导以帮助教师更好地把握课堂.有研究者提出教师可通过自我提问来思考数学步骤，调节自身学习的能力，这会反过来影响代数推理.具体表现为：知道该做什么（理解问题）；寻找全局（联系问题）；知道如何、何时和为什么做（战略问题）；监测和评价这一进程（反思问题）[32].总之，既要关注对教师适应知识内容的有效性进行分析与评估，又要通过提升教师的自我调节，优化学生对学习过程的参与.

2.3.3 教学策略

在代数推理的教与学过程中，研究者会从学习心理的角度，为增强学生的代数推理能力，提供一些教学建议.首先是确保学生具备学习新数学策略所必需的先验知识，在建模时教师可以使用“大声思考”的技巧指导学生具体的技能[3]186.其次，研究者发现学生构建知识的类型和他们形成的模式之间存在一定的联系，学生通过使用这些模式对口头表述和符号表征之间的关系进行识别和扩展[33]，图式策略有助于学生建构完整知识结构，促进其用结构和模型的思想来解决代数推理问题.第三，培养学生的符号意识，代数推理需要学生实现具体问题情境与关系表达的转化，符号意识体现的也是学生进行分析、概括与推理的代数方法.第四，多元表征，即“文字的、表格的、图形的和符号的以及各种表征之间的灵活转换”[34]，能够让学生根据具体的代数内容或自己的操作能力进行恰当的选择，有助于理解数学符号和抽象方程在具体层面上的运行，尤其对小学生有益.最后，可以实施分阶段的渐进式教学，包括从具体到抽象的解释，从简单到复杂的问题的例子，或是始于简单概念的教学[14]101.

综上可见，在早期代数中，因为学生的数学思维习惯尚不完善，教师在代数推理教学中发挥着关键的引领作用，但是，仍需学生在代数推理教学中积极进行数学思考，尤其要营造课堂“推测”氛围.因此，代数推理教学，是一个充分交流、展示、互动的教学过程.

3 结论与讨论

综合以上国外中小学代数推理研究的文献分析，对国外研究的主要成果作如下总结，并结合我国研究现状提出几点启示.

3.1 基本结论

首先，国外代数推理研究相对较为成熟，理论与实证研究相得益彰.对算术与代数、算术思维与代数思维的辨析与比较，是理解代数推理的奠基石；代数思维和代数推理的认知分析与发展策略，则指向理论到实践的过渡，最终是要发展中小学生的代数思维和代数推理能力，这是代数教学的发展目标与方向.

其次，从研究对象与研究方法来看，研究者比较关注“早期代数”的影响，因此，对小学阶段的代数思维和代数推理发展有较多的实证研究，用实验数据论证观点.

再者，从研究结果的预期发展而言，国外的代数思维与代数推理研究能够较好地用于教学实践，美国、俄罗斯、澳大利亚、新西兰等国家都有相应的教育报告或研究项目来支持中小学校中代数课程的发展，给予数学教师专业发展的培训机会，也促进学生在代数思维和代数推理方面的提升.最后，在研究基础上，国外的代数推理研究相对而言较为重视对学习心理学的研究成果的借鉴，代数推理教学的发展策略也离不开对学生心理的分析.

3.2 研究讨论

与国外相比，我国的代数推理研究还比较少，在理论与实践的相互支持以及教师专业发展上都有所欠缺.我国代数推理研究具体可从以下几个方面做出努力.

3.2.1 把握算术与代数、算术思维与代数思维的本质区别与联系

虽然有不少研究者明确提出“在算术中教代数”或者“从算术思维过渡到代数思维”，但在理解算术与代数、算术思维与代数思维时，会局限于体会数与符号的区别、程序与结构的区别，教师仍需有意识地将区别与内容联系起来，具体地就一般化、结构、关系、函数、变化、模型、问题解决等做出细致辨别，由此，或许能对每一部分的内容提出发展目标，并在算术与代数中找到相对应的联系.

3.2.2 要在问题解决中找到代数推理任务设计的思考性与连贯性

根据已有研究，代数推理任务设计有两个基本条件，一是问题解决的重点不在于得到事实性的答案，而是关注学生展开关系转化的思考过程；二是问题解决的情境创设，可以是生活情境，联系学生的生活经验，更要呈现数学情境，使学生能够学会观察、想象、描述与概括.在中小学数学课程安排上，我国主要是以“数与代数”作为一个课程领域，数与运算、数量关系、数与式、方程与不等式、函数等内容进行交叉学习，如何保持代数内容的连贯性以及与算术内容的联系，是需要考虑的问题.而且，在我国课程标准中可发现，数学推理主要强调合情推理与演绎推理能力的发展，对代数推理任务的设计也要遵循一般推理的规范.因此，为了在“数与代数”中促进学生代数推理能力的发展，任务设计需要兼顾学生认知特点、代数知识特征、一般推理规范三个方面，以满足学生展开任务过程的心理逻辑与知识逻辑.

3.2.3 关注教师代数教学内容知识的专业发展

一方面，考虑到过去常常以学生的测试成绩作为评估教师教学的标准，在代数推理教学中，学生与教师的评估方式和内容都应发生改变.代数推理作为一种思维方式，更多地表现为教师与学生的思考能力，而且代数推理中“关系的转换”需要过程性的记录，因此以定性描述来给予教师专业素养的判定是必要的.另一方面，基于社会文化的视角，代数推理教学应该是一种集体实践，教师与学生都要参与思考过程，教师才能依据对学生的“说理”过程进行思维判断，抓住代数推理引导的契机.这对教师而言，既要考虑其教学专业素养的培养，也对其代数推理专业内容知识的学习提出严格要求.

总之，国外中小学代数推理研究已经获得了较丰富的成果，并且关注到了早期阶段代数推理能力的培养，其研究关注点和研究方法等都可以为我国相关研究提供借鉴与启发.

参考文献

[1]Kieran， C.. Learning and Teaching Mathematics[J]. Psychology Press Lid， 1997 （3）： 136-137.

[2]Kaput， J.. Transforming Algebra from an Engine of Inequity to an Engine of Mathematical Power by “Algebrafying” the K-12 Curriculum[C]// National Council of Teachers of Mathematics & Mathematical Sciences Education Board （Eds.）. The Nature and role of algebra in the K-14 curriculum： Proceedings of a National Symposium. Washington， DC： National Research Council， National Academy Press， 1998： 25-26.

[3]Koedinger， N. K. R.. Teachers＼＼" and researchers＼＼" beliefs about the development of algebraic reasoning[J]. Journal for Research in Mathematics Education， 2000， 31（2）： 168-190.

[4] 全美數学理事会. 美国学校数学教育的原则和标准[M]. 蔡金法译. 北京：人民教育出版社，2004：73.

[5] Godino， J. D.， Castro， W. F.， Ake， L. P.， & Wilhelmi， M. R.. The Nature of Elementary Algebraic Reasoning[J]. Bolema-Mathematics Education Bulletin-boletim De Educacao Matematica， 2012， 26（42B）： 483-511.

[6]鲍建生，周超著. 数学学习的心理基础与过程[M]. 上海：上海教育出版社，2009：310-339.

[7] Anna Sfard. On the dual nature of mathematical conceptions： reflections on process and objects as different sides of the same coin[J]. Educational Studies in Mathematics， 1991， 22（1）： 1-36.

[8]Glassmeyer， D.， & Edwards， B.. How middle grade teachers think about algebraic reasoning[J]. Mathematics Teacher Education & Development， 2016， 18（2）： 92-106.

[9] Tall， H. D.. The general， the abstract， and the generic in advanced mathematics[J]. For the Learning of Mathematics， 1991， 11（1）： 38-42.

[10] Booth， G.. Dynamic representation and the development of a process understanding of function Research[J]. Issues in the Learning and Teaching of Algebra， 1988， 4（3）： 11-15.

[11] Berlin， D. F.， & Hillen， J. A.. Making connections in math and science： identifying student outcomes[J]. School Science and Mathematics， 1994， 94（6）： 283-290.

[12] Pitta-Pantazi D.， Chimoni M.， Christou C.. Different types of algebraic thinking： an empirical study focusing on middle school students[J]. International Journal of Science and Mathematics Education， 2020， 18（5）： 965-984.

[13]Blanton， M.L.， & Kaput，J.J.， Elementary Grades Students' Capacity for Functional Thinking[J]. International Group For The Psychology Of Mathematics Education， 2004：136.

[14]Basir M A， Waluya S B. How Students Use Cognitive Structures to Process Information in the Algebraic Reasoning？[J]. How Students Use Cognitive Structures to Process Information in the Algebraic Reasoning？， 2022， 11（2）： 821-836.

[15] Fonger， N. L.， Stephens， A.， Blanton， M.， & Knuth， E.. A Learning Progressions Approach to Early Algebra Research and Practice[C]. 37th annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education， 2015：201-204.

[16] Harper， E.. Ghosts of Diophantus[J]. Educational Studies in Mathematics， 1987， 18（1）： 75-90.

[17] Lepak， J. R.， Wernet， J. L. W.， & Ayieko， R. A.. Capturing and characterizing students strategic algebraic reasoning through cognitively demanding tasks with focus on representations[J]. The Journal of Mathematical Behavior， 2018， 50： 57-73.

[18] Powell， S.R.， Mason， E.N.， Bos S E， et al. A Systematic Review of Mathematics Interventions for Middle‐School Students Experiencing Mathematics Difficulty[J]. Learning Disabilities Research And Practice， 2021， 36（4）：295-329.

[19]張春莉. 小学生数学能力评价研究[M]. 北京：人民教育出版社，2010：28-30.

[20] Siemon， D.， Day， L.， Stephens， M.， Horne， M.， Callingham， R.， & Watson， J.. Reframing Mathematical Futures： Using Learning Progressions to Support Mathematical Thinking in the Middle Years. 40 years on： We are still learning！[C]// Proceedings of the 40th Annual Conference of the Mathematics Education Research Group of Australasia. Melbourne： MERGA， 2017： 651-654.

[21] Indraswari， N. F.， Budayasa， I. K.， & Ekawati， R.. Algebraic reasoning in solving mathematical problem based on learning style[J]. Journal of Physics： Conference Series， 2018， 947： 012061.

[22] Walkington， C.， Petrosino， A.， & Sherman， M.. Supporting algebraic reasoning through personalized story scenarios： how situational understanding mediates performance[J]. Mathematical Thinking & Learning， 2013， 15（2）： 89-120.

[23] Powell， S. R.， & Fuchs， L. S.. Does early algebraic reasoning differ as a function of students difficulty with calculations versus word problems？[J]. Learning Disabilities Research & Practice， 2014， 29（3）： 106-116.

[24] Ana， S.， Andreja， B.， Andrija， V.， & Maja， P.. Development of abstract mathematical reasoning： the case of algebra[J]. Frontiers in Human Neuroscience， 2014， 8： 679.

[25] Carpenter， T. P. & Levi， L.. Developing conceptions of algebraic reasoning in the primary grades[C]. Paper presented at the Annual Meeting of American Educational Association， Montreal， Canada， 2000： 3.

[26] Christine Ormond. Two key ways to establish some early algebraic ideas in primary classroom[J]. APMC， 2012 （17）： 13-18.

[27]章勤瓊，谭莉. 早期代数思维的培养：小学阶段“数与代数”教学的应有之义[J]. 江苏教育，2013（33）：7-9.

[28]张文宇，傅海伦. 新西兰小学运算能力项目的影响及启示[J]. 外国中小学教育，2010（05）：48-53.

[29] Tunks， J.， & Weller， K.. Changing Practice， Changing Minds， from Arithmetical to Algebraic Thinking： An Application of the Concernsbased Adoption Model（CBAM）[J]. Educational Studies in Mathematics， 2009， 72（2）： 174.

[30] Bair， S. L.， & Rich， B. S.. Characterizing the development of specialized mathematical content knowledge for teaching in algebraic reasoning and number theory[J]. Mathematical Thinking and Learning， 2011， 13（4）： 292-321.

[31] Hunter， J.. Teacher actions to facilitate early algebraic reasoning[J]. Mathematics Education Research Group of Australasia， 2015：58-67.

[32]Kramarski， B.. Promoting teachers algebraic reasoning and self-regulation with metacognitive guidance[J]. Metacognition and Learning， 2008， 3（2）： 83-99.

[33] Steele， D. F.， & Johanning， D. I.. A schematic“theoretic view of problem solving and development of algebraic thinking[J]. Educational Studies in Mathematics， 2004， 57（1）： 65-90.

[34] Choike， J. R.. Teaching strategies for “algebra for all”[J]. The Mathematics Teacher， 2000， 93（7）： 556-560.

作者简介 谢春艳（1996—），女，湖南邵东人，教育学硕士;主要从事数学教育研究.

黄娜娜（1996—），女，内蒙古通辽人，硕士研究生;主要从事数学教育研究.

潘禹辰（1998—），女，江苏苏州人，硕士研究生;主要从事数学教育研究.

徐文彬（1966—），男，安徽宣城人，教授，博士生导师;主要从事数学教育研究.