是巧合还是必然

程峰 鲍光发

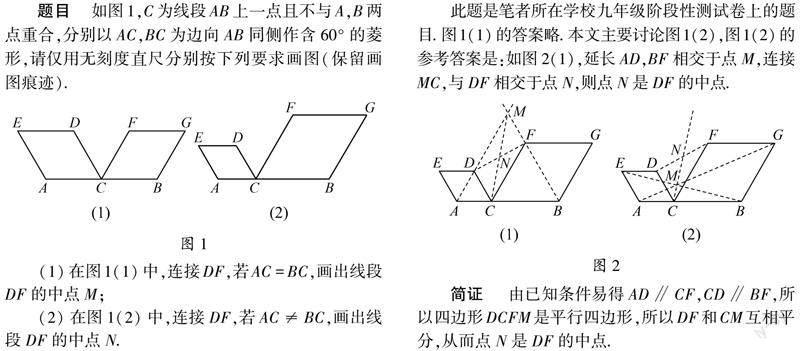
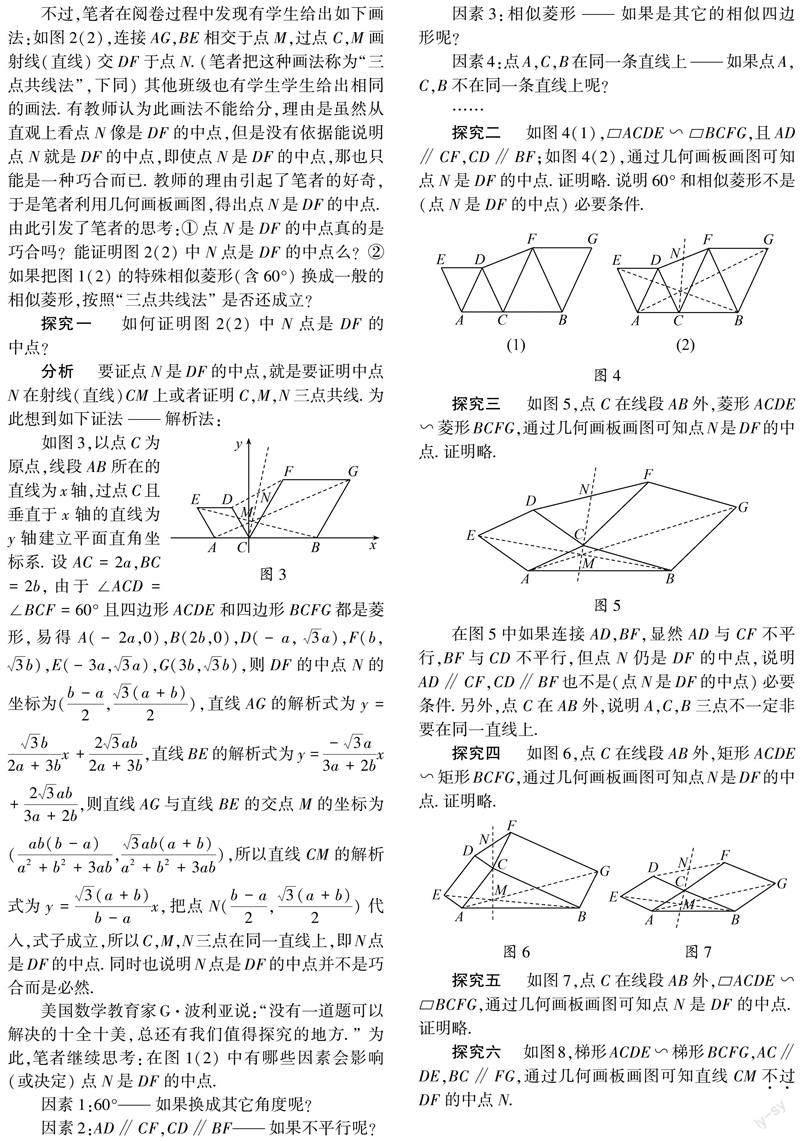
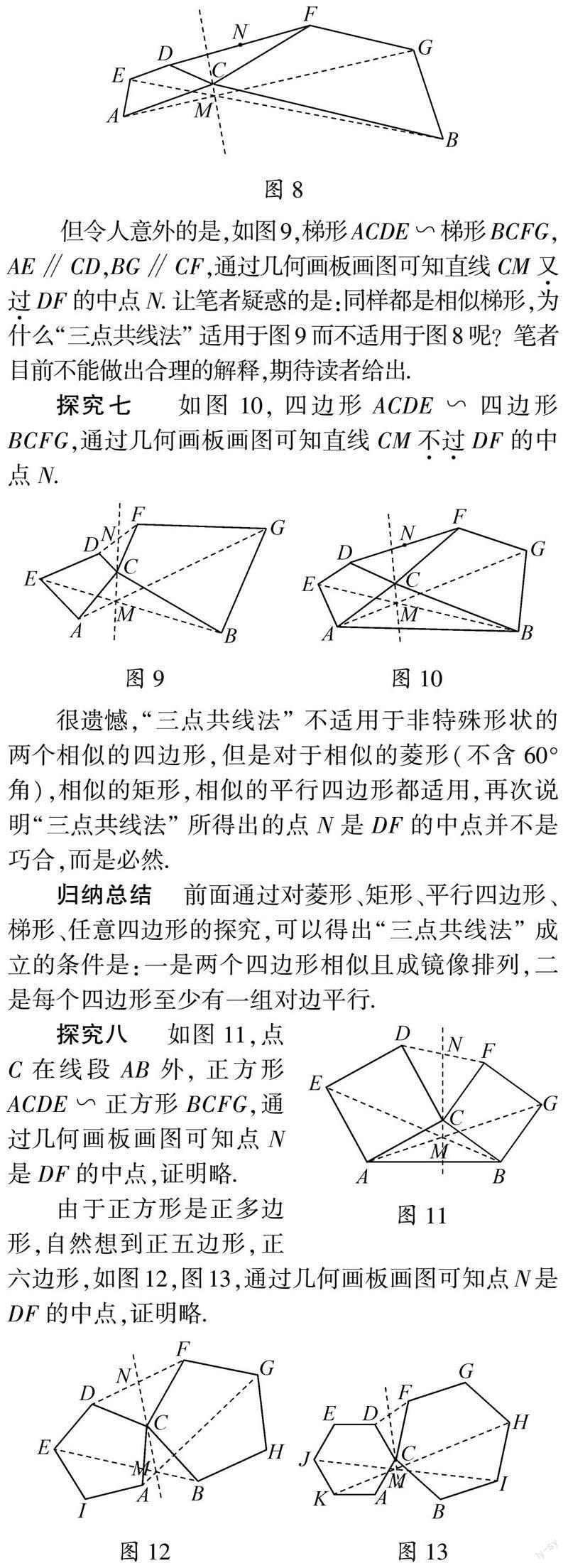
【摘 要】 一道用无刻度直尺的画图题，由于学生的画法不同于参考答案且难以确定画法是否正确，因此被老师认为是巧合，缺乏依据，从而引发了笔者的思考和探究.

【关键词】 巧合；必然；相似菱形；探究；三点共线法

显然“三点共线法”还适用于正多边形（正四边形，正五边形，正六边形），由此猜想“三点共线法”适用于正n边形（n≥4）.

笔者在讲评试卷时花了大半节课专门讲解此题，学生既兴奋又惊讶，纷纷发出感叹，一道小小的画图题竟然可以挖掘出这么多相关的问题.

教学启示

1.思画法之理，提升思维的严密性

有许多学生在解决仅用无刻度直尺的画图题时，毫无目的地用刻度尺把所有能连的两个点连起来，线是画了不少，但是没能找出真正有用的点或线，导致问题还是没有解决.即使碰巧画对了，思维也没得到任何提升.笔者在教学时要求学生在连线的过程中就要边思考，为什么要连这条线，有什么用途，依据何在，也就是明确画法后面隐藏的道理，经常这样思考，就能形成良好的合乎逻辑的思维品质，从而提升思维的严密性.本题运用解析法证明了点N是DF的中点，让学生理解“三点法”的依据，打消了学生的疑惑，让学生知其然也知其所以然.

2.悟一法多用，培养思维的发散性

在教学过程中，要从不同的认识层次，观察角度，知识背景和问题特点进行一题多变，一法多用，这样不仅能调动学生学习数学的兴趣，养成积极思考的习惯，而且能培养学生深度思考和分析问题、解决问题的能力，从而在潜移默化中提升发散性思维.本题从特殊的菱形到一般菱形到矩形到平行四边形再到正多边形，发现用“三点法”都可以找到DF的中点，这样学生对“三点法”有了更深层次的理解，同时也培养了学生思维的发散性.

3.明探究过程，培养探究能力

数学新课标的理念之一是“自主探究，合作交流”.如何让学生有自主探究的意识，知道怎样去探究，笔者认为教师自己首先要有自主探究的意识和习惯，才能更好地引领学生探究.教师要善于发现值得去探究的资源.本题笔者用几何画板验证了点N是DF的中点，并给出了证明，但并没有就此停下，而是进行更深层次的思考和探究.在讲解此题时，笔者把对此题的探究历程展示给学生，让学生对“探究”一词有更深层次的认识和理解，当然对此题也有了新的认识和理解.

参考文献

[1]周炼.谈“作图题”教学[J].中小学数学（初中版），2020（9）：39-42.

[2]易良斌.注重几何直观强化逻辑推理丰富数学模型——2018年杭州市中考數学第23题赏析及教学启示[J].教学月刊·中学版（教学参考），2018（10）：58-62.

作者简介

程峰（1975—），男，中小学高级教师;主要研究课堂教学、解题（变式）教学等;发表文章20余篇.

鲍光发（1971—），男，中小学高级教师;主要研究初中数学课堂教学;曾获市级比赛课一等奖.