NAPLAN考查“测量”内容的试题研究
海洋 吴红德 林子植


【摘 要】 “测量”内容作为义务教育阶段数学课程标准中数与代数内容领域的重要组成部分,对培养学生的“数感”“量感”有着重要作用.文章从考查的试题主题与标准、试题分布、试题特征三方面出发,对NAPLAN义务教育阶段的试题进行分析研究.结果表明,对“测量”内容的试题命制应该以学业质量标准为基础,尊重学生个体差异,选择合适的测量工具的同时还要注重试题情境的现实性,以真正激发学生的数学兴趣.
【关键词】 澳大利亚;NAPLAN;测量;试题内容
自2001年颁布的《全日制义务教育数学课程标准(实验稿)》中提及“数感”到《义务教育数学课程标准(2011年版)》将“数感”作为数学十大核心词之一,再到《义务教育数学课程标准(2022年版)》(以下简称“新课标”)再次明确要着力培养学生的“数感”与“量感”可以发现,“测量”作为新课标下课程内容的重要组成部分,始终贯穿于我国义务教育的各个阶段.新课标在描述二者时指出:“数感”是指对于数与数量、数量关系及运算结果的直观感悟;“量感”则是指对事物可测量属性及大小关系的直观感知[1].其内容的学习是培养学生“数感”与“量感”的重要途径[2],也是学生深入学习数学的重要前提.因此,深入研究“测量”内容领域是必要且有深刻意义的.但通过对相关文献的梳理发现,我国关于“测量”内容的相关研究较少,需要更多的借助已有测试项目的成功经验.
澳大利亚全国读写与数学能力评估项目(National Assessment Program—Literacy and Numeracy,NAPLAN)作为澳大利亚政府在国家层面按照统一评价标准开展的基础教育质量评价活动,可以使澳大利亚政府、教育当局和学校通过其评价结果来确定澳大利亚学生是否达到了良好的教育成果[3].其在考查“测量”内容的试题方面,具有较为成熟的实践经验.基于此,本研究以“NAPLAN试题中如何考查‘测量内容”为问题主线,从有关“测量”试题的主题与标准、分布和特征三方面进行深入分析,获得启示,以期为我国基础教育阶段关于数学“测量”内容的试题命制提供有益参考.
1 NAPLAN“测量”内容的试题主题与标准分析
1.1 NAPLAN“测量”内容的试题主题
NAPLAN项目针对澳大利亚三、五、七、九年级的学生,包含4个领域的内容,分别是阅读、写作、语言(拼写、语法与标点)与数学.其中数学测试按照课程标准《The Australian Curriculum Mathematics》(《澳大利亚国家课程:数学》)[4]中设置的3个内容领域进行,即“数与代数”“测量与几何”“统计与概率”,主要评估学生对数学知识、技能和理解的语境化运用,具体分为理解、熟练、问题解决、推理四个认知水平层次.关于“测量”的知识内容主要由常见的量和几何中的量组成.常見的量主要有长度、时间、质量、容积、温度等;而几何中的量主要包括面积、周长、体积和角度.根据NAPLAN官方网站发布的信息,现对三、五、七、九年级考查的“测量”内容的主题汇总如表1所示.
从表1呈现的内容看,三年级主要考查长度、面积、体积、时间、质量、容量、周长;五年级相比三年级增加了角度内容,主要考查长度、面积、体积、时间、质量、容量、角度、周长;七年级主要考查长度、面积、体积、时间、质量、容量、角度、周长;九年级主要考查长度、面积、体积、时间、质量、角度、温度.
1.2 NAPLAN“测量”内容的试题标准
NAPLAN为“数学”测试内容设置了国家最低标准[5].分别从“数”“空间”“代数、函数和模式”“测量、概率和数据”“数学运算”这五个方面对“国家最低标准”作出了具体说明.“国家最低标准”中明确规定了三、五、七、九年级学生所应达到的最低等级要求,而测试题也是按照相应内容的水平要求进行编制的,通过测试可以了解学生的“数学”是处于、超过还是低于相应年级的“国家最低标准”.其中对“数学”的评价结果共分为10级,每个年级分别有6个不同层次的水平.3年级为1至6级,其中2级为要求达到的“最低标准”;5年级为3至8级,其中4级为要求达到的“最低标准”;7年级为4至9级,其中5级为要求达到的“最低标准”;9年级为5至10级,其中6级为要求达到的“最低标准”.现对“测量”内容的最低标准汇总如表2所示.
从表2内容中可以看出,最低标准对三年级学生“测量”方面的要求主要是对各主题内容进行简单的认识、理解、比较和简单计算;对五年级学生更加强调使用标准单位对各主题内容进行测量;对七年级学生增加了各项主题内容的测量方法、数据读取和记录、计算等方面的具体要求;而对九年级则更加强调使用国际单位进行测量和比较,更加注重运用各种简单的测量方法解决实际问题.整体看,关于“测量”内容的“国家最低标准”描述了学生在数学学科“测量”领域通常可以达到的一些最基本的知识、技能和理解水平.
2 NAPLAN“测量”内容的试题分布分析
知识是能力产生的本源,也是数学核心素养生成的本源[6].对学生“测量”内容掌握情况的考查可以通过对知识的考查来体现.因此,对考查“测量”内容的试题分布分析尤为重要.在明确了关于考查“测量”内容的主题和标准后,以NAPLAN2016年度测试卷为样本,对三、五、七、九年级考查“测量”内容在试题中的分布数量进行统计,其结果如表3所示.由表3数据可知,NAPLAN2016年测试卷在三、五、七、九年级中考查的“测量”内容涵盖了“面积、周长、角度、长度、时间、质量、容积”七个方面.
从内容维度看,考查最多的是“长度、面积、周长”三部分,其中“长度”考查了10道试题,“面积”考查了6道试题,“周长”考查了5道试题,“容积”考查了2道试题,而与“体积”相关的试题却没有被考查.从考查的各试题内容数量在不同年级的分布情况看,“长度、面积、周长”在三、五、七、九年级均进行了考查;“质量、时间、容积”主要在三、五年级进行考查,而在七、九年级考查较少,“体积”内容在三、五、七、九年级均未进行考查.
从年级维度看,三年级考查了“面积、周长、长度、时间、质量、容积”六个方面,共计9道试题;五年级考查了“面积、周长、角度、长度、时间、质量、容积”七个方面,共计10道试题;七年级考查了“面积、周长、角度、长度、时间”五个方面,共计5道试题;九年级考查了“面积、周长、角度、长度”四个方面,共计9道试题.
3 NAPLAN“测量”内容的试题特征分析
由表3数据可以看出,NAPLAN对“测量”内容各主题的考查较为丰富,既有常见的量,也有几何中的量.综合考虑小学和初中的试题均能有所列举以便于进行对比分析,现对NAPLAN测试卷中三、七年级考查“长度、面积、周长、质量、角度、时间”这六部分内容的典型试题进行举例分析,从而进一步探究NAPLAN试题是如何考查“测量”内容的.
3.1 “长度”内容试题及分析
例1 (小学三年级)艾伦有3个夹子,夹子的尺寸有小、中、大三种,图1分别显示了大夹子和小夹子的长度,则中等尺寸夹子的长度可能是多少?
1.2厘米 B.4厘米 C.6厘米 D.8厘米
例2 (中学七年级)塔妮娅有两根完全相同的塑料管,她把其中一根切成长度相等的五个部分,把另一根切成长度相等的两个部分(如图2).切完后长的塑料管比短的塑料管长9cm.请问短的塑料管长度是多少?
评析 例1考查准确读取直尺上的整数刻度值并能够测量物体的长度和比较测量值的大小;例2考查根据等量关系建立方程从而计算物体的长度.对比来看,例1的试题内容更为简单易懂,考查的内容也较为基础;例2的试题内容较显复杂,通常需要设立未知数建立方程求解;但两道试题的出题方式均以图形的方式给出,较为直观.因此,其小學阶段只需要学生掌握测量长度工具的使用和对基本概念的理解,而初中阶段则更加注重对学生分析问题和解决问题能力的培养.
3.2 “面积”内容试题及分析
例3 (小学三年级)图3中哪个灰色图形的面积最大?
例4 (中学七年级)图4显示了电视机屏幕的长度和宽度,请问电视机屏幕的面积是多少?
评析 例3考查学生对图形面积属性的理解,通过对组成灰色图形的小三角形数量的计算,从而比较图形面积的大小关系;例4考查计算长方形面积的方法,学生需能准确读取标准单位制下的长度数据并掌握计算长方形面积的方法.对比来看,例3只是考查学生对面积概念属性的理解,例4则要求学生掌握计算面积的方法,小学阶段对于知识技能的要求更低.
3.3 “周长”内容试题及分析
例5 (小学三年级)艾玛正在用回形针测量卡片的长度(如图5),则这张卡片四边的总长度是多少?
例6 (中学七年级)图6中五边形的边长均相等且为3.5cm,四块相同的五边形连在一起组成了一个更大的图形,则这个较大图形的周长是多少?
A.42cm B.49cm C.56cm D.70cm
评析 例5考查识别物体的形状并使用“回形针”这一非正式单位测量周长,通过对“回形针”数量的计算,使学生掌握长方形周长的概念和测量方法;例6考查计算组合图形的周长,通过对比单一图形和组合图形的关系,从而掌握计算组合图形周长的方法.对比来看,例5仅考查了学生对长方形周长概念属性的理解,而例6则要求学生进一步掌握计算复杂图形周长的方法.
3.4 “质量”内容试题及分析
例7 (小学三年级)瑞娜正在用天平(如图7)比较四个不同物体的重量,请问哪个物体最重?
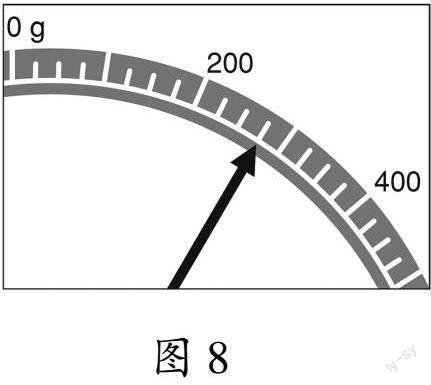
例8 (中学七年级)芬恩在厨房的秤上放了一些面粉,图8为表盘的一部分,请问芬恩在秤上放了多少克面粉?
评析 例7考查对质量的比较,学生要能够使用天平来比较物体质量的大小;例8考查对测量工具的使用,学生要能够准确识读测量工具上显示的数据.对比来看,无论是小学还是初中对“质量”内容的考查均较为基础,都是对量的属性理解、大小的比较和对工具使用等方面的考查.
3.5 “角度”内容试题及分析
例9 (小学五年级)如图9所示,一架梯子靠在墙上,梯子与地面之间标记为A的角度和90°之间的大小关系是?
例10 (中学七年级)鲁比为家里的墙壁设计了一幅长方形的画,在长方形内她添加了三条直线,如图10,则角x为多少度?
评析 由于小学三年级不考查“角度”内容,故列举五年级试题.例9考查角度大小的比较,学生要掌握直角三角形中各角度的大小关系;例10考查直角、平角的概念,学生要会根据角的概念来求未知角的角度值.对比来看,小学阶段的试题主要考查学生对具体的直角三角形的感知、认识和理解,初中阶段的试题主要考查学生对角的概念及角度关系的理解以及在此基础上的问题解决能力.两种试题均以实际生活情境为前提.
3.6 “时间”内容试题及分析
例11 (小学三年级)图11的时钟显示了某天下午两个不同的时刻,则两个时刻之间相差多少分钟?
例12 (中学七年级)田径嘉年华活动在上午10:30开始,持续了2个小时,活动结束后罗斯便直接回家了,他在路上花费了1个小时.请问罗斯什么时间到家的?
评析 例11考查准确读取模拟时钟和数字时钟上的时刻,并会计算两时刻之间的时长;例12考查计算时间段的长度并能够根据时长来推断时刻.对比来看,二者均考查学生对时刻和时长的简单识读和计算,对时间概念的基本认识和理解,小学试题的问题情境更为简洁,而初中阶段的试题情境稍显复杂.
4 结论与启示
澳大利亚NAPLAN项目中关于考查“测量”的“最低标准”的设置、内容的设置、试题的呈现方式和考查测量的方法等方面颇具特色.在标准方面,以“最低标准”为底线,研判育人质量;在内容设置方面,突出“测量”内容的丰富性和广泛性,全面夯实基础;在试题呈现方式上,以学生实际生活为背景,增加了内容的情境性、趣味性和插图的直观性;在考查测量的方法上,突出了对不同“测量”内容属性的理解、测量工具的使用和数据的计算,发展了学生“数与形”相结合的思想,提升了学生的测量能力.现将NAPLAN如何考查“测量”内容的有关结论与启示总结如下.
4.1 结论
4.1.1 以“最低标准”为底线,重视基础知识的学习
NAPLAN“国家最低标准”中明确规定了三、五、七、九年级学生所应达到的最低等级要求,通过测试可以了解学生的“数学”是处于、超过还是低于相应年级的“最低标准”.从“最低标准”所描述的行为动词看,“使用”“识别”“阅读”“比较”“应用简单的测量公式”等,这些行为动词指向了最基础的知识、技能和理解水平.从考查“测量”内容的六个主题看,所考查的试题均是对概念属性的理解、测量工具的使用和简单的计算.因此,NAPLAN“国家最低标准”对数学“测量”内容的重点描述了学生通常可以达到的一些最基本的知识、技能和理解水平,以“最低标准”为底线,重视基础知识的学习.
4.1.2 考查的测量内容丰富,使用的测量工具广泛
从NAPLAN2016年测试卷在三、五、七、九年级考查“测量”内容的分布情况可以看出,无论是内容维度,还是年级维度,NAPLAN考查的“测量”内容都较为丰富,考查“测量”试题的数量也较多.究其原因,一是“测量”内容包含了广泛的量,既有常见的量(如:长度、时间、质量、容积、温度等),也有几何中的量(如:面积、体积、周长、角度等),对这些“量”的认识增加了学生对生活的理解和体会;二是“测量”内容的应用非常广泛,如测量长度、比较长短、计算面积、称重物体、看时间等,和生活联系很紧密,体现了数学具有广泛应用的特点.
此外,从NAPLAN考查“测量”内容的试题来看,考查“长度”时用到了标准测量工具——直尺;考查“周长”时用到了非标准测量工具——回形针;考查“质量”时分别用到了天平和磅秤;考查“时间”时用到了模擬时钟和电子时钟.整体看,考查测量工具的使用较为广泛,也间接说明对于“测量”内容的考查离不开对测量工具使用的考查.
4.1.3 以问题解决为导向,试题突出真实情境
从考查“测量”内容的试题来看,试题以问题解决为导向,而数学问题本身就是一种情境,不同的问题展示了不同的情境,但NAPLAN试题突出了实际问题和真实情境.无论是试题文字语言还是试题所对应的配图,都描述和展示了生活中的真实场景和真实物体,在阅读试题时能充分的感受到问题场景,符合生活经验,具有一定的阅读性.如例1中考查“长度”的夹子、例4中考查“面积”的电视机、例9中考查“角度”的梯子等,这些试题都描述了现实生活中的真实场景,“夹子”“电视机”“梯子”等都是真实物体,其将知识的考查与问题的解决联系起来,使真实情境贯穿始终.
4.2 启示
4.2.1 以学业质量标准为基础命制试题内容
新课标对学生所要学习的内容和要求进行了较为明确的规定,学生在完成本学科课程学习任务后,学业成就表现是否达到了学业质量要求是我们关心的重点问题,因为它将影响学生的自身发展.而学业质量标准是以本学科核心素养及其表现水平为主,同时结合课程内容,对学生学业成就表现的总体刻画.根据课程标准中不同内容、不同认知水平要求来命制不同难度等级的“测量”试题对于不同年龄阶段、不同学段的学生来说是十分重要且有效的.因此,在命制“测量”内容的相关试题时应充分依据新课标中的学业质量标准.
4.2.2 尊重学生个体差异,选择符合特征的测量工具
每个人都是独立的个体,不同年级、不同个体之间均存在着或多或少的差异.比如,小学生正处于接触大千世界的启蒙期,他们对于现实世界的认识还比较少、比较基础,他们更多需要的是去感知、去体验;而中学生已经对客观世界积累了一定的认识,心理有了一定程度的发展,他们需要对现实世界中更复杂、更细致的内容进行深入了解与学习.因此,在考查“测量”内容的试题时应该考虑到学生的个体差异和年级差异等因素,选择符合学生认知特征的测量工具,适时提升他们关于“测量”内容的理解和运用水平.
4.2.3 注重试题情境现实性,激发学生数学学习兴趣
从数学学习的认知本质看,数学学习离不开数学情境[7].数学情境主要是指现实情境、纯数学情境与科学情境.数学问题往往包含于各种实际情境当中,或是对各种情境的高度概括和归纳,或是对各种情境的抽象和理解.新课标明确指出“从现实生活或具体情境中抽象出数学问题”“在具体情境中,能进行简单的估算”“体验从具体情境中抽象出数的过程”等等,均表明了情境的重要性.因此,在考查“测量”内容的试题时应突出情境化特征,并与现实情境相关联,使得真实问题从真实生活中来,这样便可使抽象的问题具体化,有利于增强学生对试题理解的同时激发他们对“测量”相关知识的学习兴趣.
参考文献
[1]中华人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京:北京师范大学出版社,2022.
[2]朱丽梅,张廷艳.中日韩义务教育阶段数学课程标准“测量”领域比较研究[J].教师教育学报,2020,7(05):104-111.
[3]National Assessment Program:Literacy and Numeracy.2016 Information for Parents and Carers[EB/OL].(2022-3-16)[2022-11-05].http://www.nap.edu.au/_resources/NAPLAN_2016_information_for_parents_web.pdf.
[4]Australian Curriculum,Assessment and Reporting Authority(ACARA).The Australian Curriculum:Mathematics[EB/OL].(2012-04-29)[2022-11-05].http://www.australiancurriculum.edu.au/Mathematics.
[5]National Assessment Program:Literacy and Numeracy.National Minimum Standards:Numeracy[EB/OL].(2022-3-16)[2022-11-05].http://www.schools.nsw.edu.au/learning/712assessments/naplan/nms/numeracyYr7.html.
[6]喻平.基于核心素养的高中数学课程目标与学业评价[J].课程·教材·教法,2018,38(01):80-85.
[7]黄翔,李开慧.关于数学课程的情境化设计[J].课程·教材·教法,2006(09):39-43.
作者简介 海洋(1990—),男,硕士生,主要从事数学教育研究.
吴红德(1999—),男,硕士生,主要从事数学教育研究.
林子植(1983—),男,博士、副教授、硕士生导师,主要从事数学教育研究.
中学数学杂志(初中版)2023年1期
