阿伏伽德罗常数测定实验的改进
庞明伦


摘要:利用实验室常用的玻璃类分析仪器和电化学实验相关装置,并衔接目前中学生可能的接受程度和化学课程标准对实验技能的基本要求,设计了操作简便且结果较准确的阿伏伽德罗常数的测定方法,可供有需要的教师做参考选用。
关键词:阿伏伽德罗常数测定;实验改进;实验探究
物质的量作为微观和宏观层次的“桥梁”,通过阿伏伽德罗常数和摩尔质量,将微粒个数和物质质量联系起来,揭示出物质之间的计量学关系[1]。阿伏伽德罗常数测定过程中有三个重要的里程碑, 分别由洛施密特[2]、爱因斯坦[3]、让佩兰相继发现。后续亦有诸多如电化学分析法[4]、晶体结构分析法[5,6]、单分子膜法[7-9]、黑体辐射法,α粒子计数法,平方差法等,带动了高端测量方法的发展。
目前教材并未对阿伏伽德罗常数的测定方法作详细理论描述,也没有设计测定阿伏伽德罗常数的学生实验。电化学和晶体结构是化学选修部分的内容。结合目前中学生可能的接受程度和化学课程标准对实验技能的基本要求,设计了以电化学和晶体结构知识点为基础的两种测定阿伏伽德罗常数的学生实验,该方法操作简单,结果较准确,药品价廉无害。通过一些实验基本操作,和“数格子”数据矫正法,锻炼了学生的实验技能。
1实验方法
1.1电化学分析法
1.1.1实验原理:
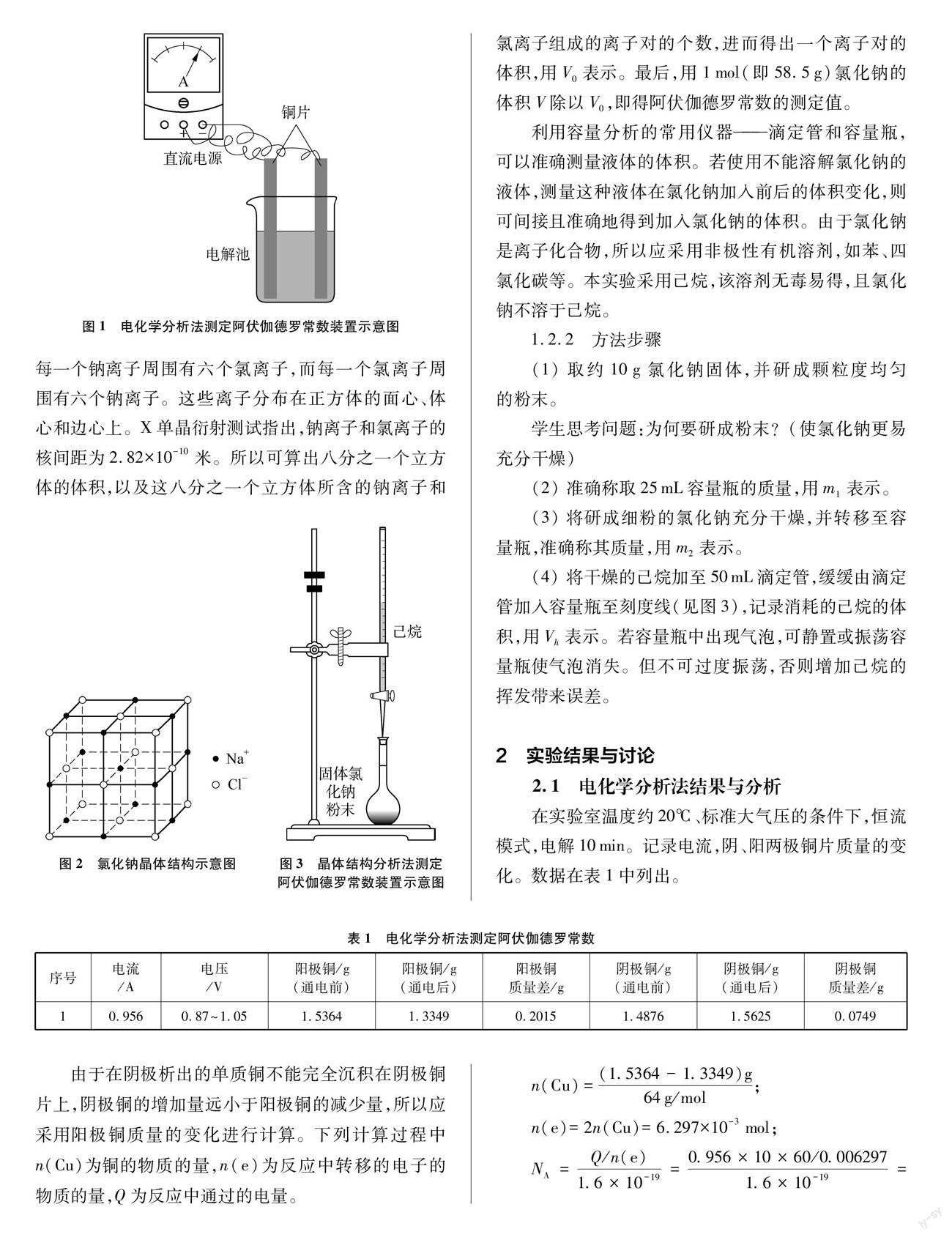
实验选用铜片作为阴阳两极,硫酸铜溶液为电解质溶液,用普通直流电源电解。
利用法拉第定律,计算出电解过程中通过的电量Q=I×t,(I: 电解电流,t: 电解时间);结合阳极铜片质量的减少量和化学计量关系,计算出电解过程中通过的电子的物质的量n(e)= ∆m/64×2,(∆m:铜片的质量变化,64:铜的摩尔质量数值,2:铜的化合价),从而计算出1 mol电子的电量为Q/n(e),最后用1 mol电子的电量除以单个电子的电量(1.6×10-19库伦),可得阿伏伽德罗常数的测定值NA = □(□(Q⁄n(e) )/〖1.6×10〗^(-19) )。
1.1.2方法步骤:
(1)在100 mL烧杯中配置50 mL约0.2 mol/L的硫酸铜溶液
(2)准备两片约1 cm×8 cm的铜片,用砂纸打磨后,在分析天平上准确称其质量。
(3)将打磨后的两片铜片的一端分别浸至硫酸铜溶液中,另一端用导线分别与直流电源的正、负极相连,如图1所示。
(4)采用恒流模式进行电解。调整电流和电压,将电流控制在1安左右,电解10分钟。
(5)小心取出二铜片,用去离子水冲去铜片上附着的溶液;晾干称重。
1.2晶体结构分析法
1.2.1实验原理
使用X射线衍射可以精确测定晶体结构。图2为由X单晶衍射测出的氯化钠晶胞绘制图。可以看出,每一个钠离子周围有六个氯离子,而每一个氯离子周围有六个钠离子。这些离子分布在正方体的面心、体心和边心上。X单晶衍射测试指出,钠离子和氯离子的核间距为2.82×10-10米。所以可算出八分之一个立方体的体积,以及这八分之一个立方体所含的钠离子和氯离子组成的离子对的个数,进而得出一个离子对的体积,用V0表示。最后,用1 mol(即58.5 g)氯化钠的体积V除以V0,即得阿伏伽德罗常数的测定值。
利用容量分析的常用仪器,滴定管和容量瓶,可以准确测量液体的体积。若使用不能溶解氯化钠的液体,测量这种液体在氯化钠加入前后的体积变化,则可间接且准确地得到加入氯化钠的体积。由于氯化钠是离子化合物,所以应采用非极性有机溶剂。如苯、四氯化碳等[6]。实验采用己烷,该溶剂无毒易得,且氯化钠不溶于己烷。
1.2.2方法步骤
(1)取约10 g氯化钠固体,并研成颗粒度均匀的粉末
学生思考问题:为何要研成粉末?(使氯化钠更易充分干燥)
(2)准确称取25 mL容量瓶的质量,用m1表示
(3)将研成细粉的氯化钠充分干燥,并转移至容量瓶,准确称其质量,用m2表示
(4)将干燥的己烷加至50 mL滴定管,缓缓由滴定管加入至容量瓶至刻度线(见图3),记录消耗的己烷的体积,用Vh表示。若容量瓶中出现气泡,可静置或振荡容量瓶使气泡消失。但不可过度振荡,否则己烷挥发带来误差。
2实验结果与讨论
2.1电化学分析法结果与分析
在实验室温度约20℃,标准大气压的条件下,恒流模式,电解 10 min。记录电流,阴、阳两极铜片质量的变化。数据在表1中列出
由于在阴极析出的单质铜不能完全沉积在阴极铜片上,所以阴极铜的增加量远小于阳极铜的减少量。所以应采用阳极铜质量的变化进行计算。下列计算过程中 n(Cu)为铜的物质的量,n(e)为反应中转移的电子的物质的量,Q为反应中通过的电量。
n(Cu) = ((1.5364-1.3349) g)/(64 g/mol) ;
n(e) = 2 n(Cu) =6.297×10-3 mol
NA = □(□(Q⁄n(e) )/〖1.6×10〗^(-19) ) = □(□((0.956×10×60)⁄0.006297)/〖1.6×10〗^(-19) ) = 5.70×1023 mol-1
由上述结果可以看出,测定值与理论值6.02×1023较为接近,误差为5%。由开始时电流不稳定,高于记录值0.956安导致。雖使用电流传感器装置进行积分矫正可减少误差,但是需要复杂设备[10]。为此,可采用“数格子”的面积矫正法。此法要求在前期电流未稳定时,每10秒读一次电流值,直至电流稳定至0.956安。将数据绘图,以电流为纵轴,电解时间为横轴(图4)。曲线下的面积即为矫正后通过的电量。矫正值为590库伦。用此矫正值进行计算,可得阿伏伽德罗常数的实验值为5.86×1023,已经十分接近理论值。
2.2晶体结构结果与分析
在实验室约20℃,标准大气压的条件下,测定粉末状固体氯化钠的体积。数据在表2中列出。
由氯化钠晶胞的八分之一个立方体计算一个离子对的体积。
八分之一个立方体的体积为(2.82×10-8)3 =2.24×10-23 cm3;在每个八分之一立方体中,钠离子和氯离子分别在顶角,且数量为4个,所以钠离子和氯离子在每个八分之一立方体中的实际个数均为1/8× 4 =1/2个;即每个八分之一个立方体含有0.5个离子对,体积为2.24×10-23 cm3;所以,每个离子对的体积为4.48×10-23 cm3。
由于加入20.42 mL己烷即达25 mL容量瓶刻度线,所以氯化钠的体积即为4.58 cm3,其质量为9.5633 g。所以1 mol (即58.5 g)氯化钠的体积为 V (1 mol NaCl) = 58.5 × 4.58/9.5633 =28.02 cm3
NA = (V (1 mol NaCl))/〖4.48×10〗^(-23) = 28.02/〖4.48×10〗^(-23) =6.25 ×1023 mol-1
由上述结果可以看出,实验测定数据与文献数据6.02×1023 mol-1较为接近,误差约为4%。由于每个离子对的体积为较精确的测量数据,本测定实验导致误差可能与所用的氯化钠没有充分干燥、己烷的挥发和己烷分子与氯化钠离子不是完全互斥等因素有关。
3结语
电化学和晶体结构法测定阿伏伽德罗常数的方法操作简单且实验结果较准确。一般学校均有相关实验器材,可作为普遍通用的学生实验。电化学法测定阿伏加德罗常数,向学生展示阴、阳两极发生的变化。学生亲自搭建电解池,对学习电化学非常有帮助。值得一提的是,国内教材对实验数据的处理方法提及较少,面对得到的实验数据,学生往往不知如何下手。由于直流电源自身不稳定,学生可学习面积矫正法,优化得出结论。
相似的,在晶体结构测定法中,学生练习了滴定管、容量瓶等容量分析仪器的操作,这些操作细节经常以考题的形式出现。最后,分析实验过程中的各个因素,如己烷挥发,研磨不彻底影响干燥等,对实验结果造成偏高或偏低的影响,是锻炼学生逻辑思维能力的有效要素。
参考文献:
[1]马艳秋. 物质的量教育学设计[J]. 中学化学教学参考, 2007, (10):9-11
[2]杨旭东. 阿伏伽德罗常数测定中的三个里程碑[J]. 化学史,2006, (10):33-35;
[3]爱因斯坦文集. 第二卷[M]. 北京:商务印书馆. 1977.
[4]Lawrie Ryan, Roger Norris. Cambridge AS and A Level Chemistry Coursebook, 2nd edition, 277-278;
[5]2001年烟台市检测题
[6]张八合. 阿伏伽德罗常数的测定[J]. 中学化学教学参考,1998, (7): 36
[7]易洪.阿伏加德罗常数测定的新进展[J].计量学报,2007, 28(4): 394-399
[8]朱纪飞,李连结. 阿伏伽德罗常数测定实验探析[J]. 实验教学与仪器, 2004, (1): 22-23
[9]趙玉玲. 中学化学教学中进行科学方法教育的探索[J]. 山东教育, 2001, (7):61-62
[10]彭捷,唐群. 基于电流传感器的NA测定[J]. 化学教学,2009, (11): 11-13

