在直观操作中体验,在体验中发展数学思维
张蕾


[摘 要] 教师应加强直观操作教学,添加让学生动手操作的内容,让学生直接借助“眼、手、口、耳”多感官去感知事物,以获得具象的体验,深化对所学知识的理解,发展数学思维。文章阐述了直观操作的几种做法,以期让直观操作发挥其教学价值,促进学生有效学习数学。
[关键词] 直观操作;数学思维;体验
数学具有很强的抽象性与逻辑性,小学生的思维是具象且感性的,因而对于抽象思维较为薄弱的小学生而言,抽象的数学知识常常令他们望而生畏。事实上,倘若教师能从小学生的思维特点出发,借助具体实例、直观展示、直接接触或生动描述向学生“讲述”数学理念,则可以让数学教学更生动、更形象。为此,教师应加强直观操作教学,添加让学生动手操作的内容,让学生直接借助“眼、手、口、耳”多感官去感知事物,以获得具象的体验,深化对所学知识的理解,发展数学思维。那么,教师该如何实施直观操作教学呢?笔者现以小学数学日常教学为例,结合自己的教学经验,谈谈做法与想法。
一、身体触摸,开启发现之旅
几何直观是一种意识,普遍存在于学生的数学学习中,并渗透于数学教学的过程中。事实上,教材中设计的丰富多彩的活动形式都能引领学生去触摸、观察、测量、实验,同时调动他们的视、听、触等感官进行思维活动。因此,日常教学中,教师也需要注重挖掘与培养的方式,通过身体触摸,引领学生开启发现之旅,为学生学习数学插上腾飞的翅膀。
案例1 圆的认识
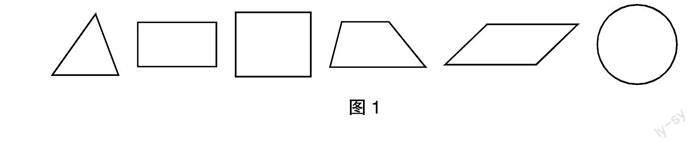
师:大家看,这是什么形状?(教师缓慢地从一个信封中掏出一个圆形的纸片,在学生观察之后又放回了信封,信封内装有图1所示的各种形状纸片)
生(齐):圆形。
师:我们从这个信封中将圆摸出来,有没有难度?
生1:一点都不难。
师:为什么?请说说你的想法。
生1:圆没有角,是曲线结构,其他的图形都有角,所以一摸就摸出来了。
师:非常好。那大家看,老师手上的这个图形是没有角的,你是否会错误地将它摸成圆呢?(教师高举一个椭圆形纸片)
生2:也不会。
师:为什么呢?
生2:圆是平滑而饱满的,它不是。
生3:这个椭圆有些部位的弧线十分平缓,有些部位的弧线十分急促,而圆每个部位的弧线都是一样的。
师:那下面哪位同学愿意来试一试,摸一摸圆呢?(学生争先恐后地举手,之后教師抽取部分学生上台,并将这些图形一一放在学生手中,让学生判断是否为圆)
……
对于学生而言,通过“摸”这样的身体触摸方式去获得数学知识是一种重要的学习方法。在触摸的过程中,学生随时都在思考。唯有这样,才能在操作中发展学生的思维,让思维向着更深处迈进。以上教学过程中,教师倘若仅仅是让学生通过“看”这种视觉感官来认识圆,则学生的思维量是很少的。因此教师在视觉感知的背景下,让学生用手触摸,从而有效地融合了视觉与触觉,深化了学生对“圆”的直观感知。显然,这样的教学过程有效提升了几何直观的教学成果,更重要的是通过具有数学味的数学探究过程,调动了学生的思维经验,让学生的智慧源源不断地从指间流淌出来,使学生获得更加深刻的学习体验。
二、使用学具,展开思维盛宴
小学数学教学离不开学具的应用,教师需要充分利用好学具,以直观方式给予学生充分的活动时间和思维空间,让学生通过学具的感知、操作和体验,展开思维盛宴,学会科学探索的方法,以获得思维的历练和发展。
案例2 角的度量
师:通常有一个专门的单位用于角的度量,是什么?
生1:度。
师:很好,大家看,三角尺上一共有三个角,大家试着描一描最小的那个角。(教师高高举起手中的一个三角尺,学生在教师的安排下动手操作)
师:你们描得真好,那有谁知道这个角的度数?
生2:我记得老师上次说过这个角是30度。
师:的确是30度(教师及时在刚刚描下的角上标出“30°”)。
师:现在有了这个角,我们就可以度量所有的……
生(齐):30°的角。
师:非常好,那这个第二大的角又是多少度呢?你们猜一猜。(指着三角尺上的另一个角)
生3:60°
师:不错,有了这个角,我们就可以度量所有的……
生(齐):60°的角。
师:大家也把它描下来,不过我们可以把它与刚才30°的角画在一起。大家试一试。(学生开始描角,教师巡视)
师:你们画得真不错!大家一起来看图2,这是最标准的画法。现在有了这个工具,我们不仅可以度量所有的30°角,还可以度量所有的60°角。
师:若再加上一个又一个的角,这个度量工具是不是会更加强大呢?(学生开始尝试,并生成了图3图6所示的作品)
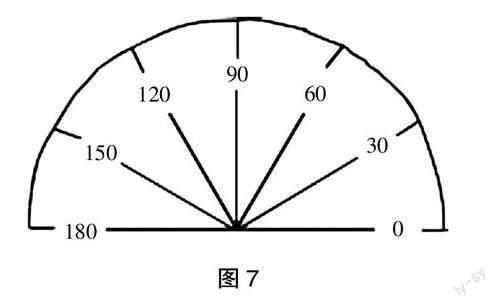
师:哇,你们的作品中出现了功能最强大的度量工具,下面我们一起改造一下图6,就这样细细地分一分刻度,大家看,现在你们发现了什么?(教师一步步地将图6改造成图7的模样)
生4:这不就是我们的量角器吗?
师:是吗?大家一起来对比一下……
以上教学中,教师精心设计,将学习量角器演变为制作量角器,让学生通过动手操作深入理解了量角器的制作原理,从而突破了教学重难点,提升了学生的动手操作能力和数学思维能力。
三、行为演绎,促进思维深化
教学数学不仅需要让学生掌握数学知识,还需要发挥数学对学生思维能力和创新能力培养方面的重要作用。行为演绎是直观操作的灵魂,是学生直观获取抽象知识的重要策略。因此,教师需要关注学生的直观感受,让学生在行为演绎中获得感知与体验,促进思维深化。
案例3 以一道思考题的探究为例
师:倘若想要连接两根绳子,该如何操作?
生1:打结。
师:谁用绳子打过结?(大家都摇头表示没有)
师:那你们会打结吗?(学生又一次搖头)
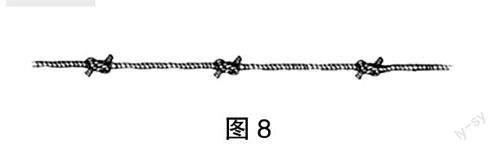
师:那我们一起来观察一下图8,绳子相连和我们平时手拉手像不像?
生2:特别像。
师:那我们就假扮成“小短绳”,自己来打一打结,如何?(有两个学生自告奋勇上来打结)
师:现在大家看,连结两根绳子需要打多少个结?
生3:1个。
师:再来一根“小短绳”,现在需要打多少个结?(又有一个学生加入)
生4:2个。
……(就这样逐一增加“小短绳”,一直到8根“小短绳”拉手站成一排)
师:现在需要打多少个结?
生5:7个。
师:从刚才的操作中,你们有何发现?
生6:每增加一根绳子,结也随之多1个。
生7:接下来,9根绳子就需要打8个结,10根绳子就需要打9个结……
对于低学段的小学生而言,抽象知识的生成往往需要附着于直观的操作之中,只有这样,他们才能清晰而深刻地领悟知识。以上案例中,对于这样一道思维含量较高的思考题,教师通过创设“小短绳打结”的情境,让学生体验打结这一有趣的数学现象,随着绳子的增加,学生也经历了从简单到复杂的探究历程,自然而然地发现了其中蕴含的规律,并举一反三地概括出其中蕴含的结论。这是一个通过直观操作深化思维的过程,通过提供给学生适当的活动方式,为学生留下了更多的活动空间和思考余地,进而水到渠成地促进了学生思维的深化。
总之,学生的学习并非被动接受知识,所有的新知学习都需要通过自身的再创造进行内化,进而转变为他们自己的认知结构。这就需要数学教师牢牢把握小学生的思维特征,借助身体触碰、使用学具和行为演绎,为学生提供好的直观操作的做法,让学生在感知和体验的同时锻炼动手能力,进一步发展数学思维。当然直观操作的方法不止这几种,教师需要充分挖掘直观操作的各种有效做法,用真正富有生命价值的方法去浸润思维、能力处于发展中的小学生,让直观操作发挥其应有的教学价值,促进他们有效学习数学。

