基于复杂度与性能联合优化的卫星导航信号捕获方法

张鹏程，黄新明，侯林源，李井源，欧钢

(国防科技大学电子科学学院,长沙 410073)

0 引言

信号捕获是导航接收机的重要组成部分，捕获性能和捕获计算复杂度会影响整个导航系统的工作[1].与连续信号不同，短突发信号具备突发和短时的特点，突发信号的起始点、起始位置不确定，具有随机性，是一个非周期信号；短突发信号不间断传输时间太短，没有明确的定义来说明持续多长时间，导致短突发信号的捕获难度较大[2].卫星无线电定位系统(RDSS)入站信号和低轨铱星STL(Satelles Time and Location)信号，都是典型的短突发信号[3].传统的码相位并行捕获难以满足短突发信号捕获的需求，相干积分长度过长，增益下降，且快速傅里叶变换(FFT)点数较大，计算复杂度高.

目前捕获算法的优化主要集中在弱信号的捕获和提升性能上[4]，对于计算复杂度的研究相对较弱.文献[5]推导了分段相关-视频积累捕获算法的处理损耗，并采用最大处理损耗最小化准则，分析了最优中频积累时间的计算方法和变化规律，但并未给出全过程的处理损耗分析和检测损耗的解析表达式.文献[6]将捕获过程分为相关层、搜索层和判决层考虑，分别讨论每层的捕获计算量，引入单位计算复杂度下的等效理想监测能力因子，以单位计算复杂度检测性能最优为准则，提出了搜索层二维搜索的优化方法.文献[7]基于匹配滤波器和快速离散匹配傅里叶变换，提出了补偿算法，在降低性能的同时也减少了计算量.但目前尚未形成计算复杂度的详细量化分析.

根据短突发信号的特点，采用并行频率搜索的分段相关-视频积累捕获算法，将信号分段相关，可以压缩中频积累时间，扩大多普勒频率的容限，避免了大规模的FFT 运算，但计算复杂度仍有较大的优化空间.本文在详细推导捕获性能和计算复杂度的基础上，建立联合优化因子，与单一的捕获性能优化进行对比，平衡了捕获性能和计算复杂度之间的关系，此方法可用于指导卫星导航信号尤其是短突发信号的捕获模块的设计.

1 分段相关-视频积累捕获算法

信号的捕获本质上是在载波多普勒频率与码相位所构成的二维假设参数空间上进行信号检测与估计的过程[8].本文采用分段相关-视频积累捕获算法将信号均匀划分为若干段，每一段分别进行相关积累，其相关结果再进行视频积累，结合频域并行捕获算法和匹配滤波器算法，在传统匹配滤波器的基础上采用FFT 的方法实现对频域的并行搜索，提高捕获效率，具体的实现结构如图1 所示.

信号总时间为T，将信号划分为N段，中频积累时间Ta=T/N、在每段信号中有M个相关器，FFT 输入点数为M、补零至2 的整数次幂Fp，每个小的相关器相干积分点数为L，对应的相干积分时间Tc=T/(N·M).假设采样率为fs，采样间隔为Ts，每段相干点数为L，其中L=Tc×fs，每次相干积分一共M段；然后将得到的M点相干积分值进行Fp点的FFT 运算；最后进行N次后积累，可采用平方律检波的方式进行后积累.

1.1 捕获性能

捕获性能主要由捕获过程中的检测损耗决定，检测损耗是捕获算法与理想相干检测之间的差异，可以用来比较检测量之间的性能差异[9].分段相关-视频积累捕获算法主要包括L点相干积分、Fp点FFT、包络检波和N次视频后积累，对各部分信号变化进行推导，得到分段相关-视频积累快速捕获的损耗.

1)L点相干积分

分段相关-视频积累捕获算法其相干积分输出信号为

式中：C为信号功率；R(τ)为本地码与信号扩频码的自相关函数；fd为多普勒频率；ϑ=πfd×(2m+L-1)+θ0；θ0为信号初相.由码相位引起的损耗为Dcode=R2(τ)；由多普勒频率引起的损耗为

2)Fp点FFT

为便于进行FFT 运算，一般将M点数据进行补零至Fp点(Fp为2 的整数次幂)，FFT 运算表达式为

此过程是一个频率分档的过程，在进行L点相干积分之后，数据速率变为fs/L；进行Fp点FFT 运算后，频谱分辨率Δf=(fs/L)/Fp.在此频率分档下，多普勒最大频率差为

仿照第一部分计算损耗的方法，可以得出此过程的实际多普勒损耗为

考虑到多普勒频率差的上限值，此时多普勒损耗最大为

则在信号检波之前，其信噪比(SNR)为

式中：信号功率C=A2/2；自相关函数Dcode=R2(τ)=1/4(码相位相差最大为0.5 码片)；多普勒估计偏差ωd=2πfd.

3)包络检波

根据等效检波损耗可得到基于包络检波的并行频率捕获的输出SNR 为[10]

结合上述分析，可以得出FFT 输出的到包络检波器输入端的SNR 为

式中：C/N0为信号载噪比(CNR)；Fp为FFT 输出点数.故包络检波后，信号的检测损耗为

4)N次视频后积累

导航信号经过相干积分之后，输出Fp点向量，平方律检波输出判决量为Fp点向量平方求和，并取最大判决量：

式中，N为视频后积累次数.

综合式(8)～(9)，即可得到分段相关-视频积累捕获算法的检测损耗.

1.2 计算复杂度

计算复杂度可以定义为捕获过程中乘法器和加法器计算量的总和.信号总时间为T，均匀划分为N段，在每一段进行检波前中频积累，每一段相干积分时间为T/N，每T/N时间的信号数据分为M段，每个小的相关器的相干积分点数为L点(对应的相干积分时间Tc=T/(MN-1)，当采样率为fs时(对应的采样间隔为Ts)，满足L=Tc×fs=Tc/Ts，Nc表示捕获中码相位搜索单元数.

对于基2 的NFFT点FFT，复数乘法运算次数α和复数加法次数β为

一次复数乘法运算相当于4 次实数乘法加上2 次加法，一次复数加法运算相当于2 次实数加法运算，故乘法运算次数α1和加法运算次数β1为

分段相关-视频积累捕获算法的总计算复杂度如表1～2 所示.

表1 乘法器计算复杂度

表2 加法器计算复杂度

可将计算复杂度视为乘法器和加法器计算量的总和，由于每个小的相关器点数L=T fs/(MN-1)，则计算复杂度的表达式可改写为

2 最优中频积累时间

捕获算法优化通常建立在总的积累时间T给定的情况，计算最优中频积累时间，对不同频率搜索间隔、不同接收机灵敏度、不同相关器个数三种情况分别进行优化设计.在总的积累时间确定的情况下，最优分段数与最优中频积累时间可以相互转化，所以确定最优分段数的同时也就确定了最优中频积累时间.

2.1 接收机灵敏度、相关器个数给定时的不同多普勒搜索间隔

根据1.1 节分析得到的检测损耗，采用最大损耗最小化准则，最大损耗的多普勒频率偏差为频率搜索间隔的一半，故式(8)～(9)可改写为：

在分段相关-视频积累快速捕获方法中，存在一个最优的分段数和最优中频积累时间使得捕获性能最优即检测损耗Lc最小，该最优分段数和最优中频积累时间与输入SNR 和多普勒频偏大小等有关.

设定总时间T为3 ms，输入CNR 为45 dB-Hz，码相位搜索间隔为0.5 个码片，每一段相关器个数M为8，改变多普勒搜索间隔fdΔ，最大多普勒偏差fd为多普勒搜索间隔的一半，分析检测损耗与分段数N、中频积累时间Ta之间的关系，确定最优分段数Nopt、最优中频积累时间Topt、最小检测损耗Lmin和计算复杂度O0.图2 给出了不同多普勒搜索间隔时检测损耗Lc随分段数N、中频积累时间Ta的变化曲线.

图2 不同多普勒搜索间隔时Lc 随N 和Ta 的变化曲线

上述分析是建立在只考虑捕获性能的条件下，并未考虑捕获计算复杂度的影响，为了适应低功耗、短突发信号捕获等场景，需要对捕获算法的计算复杂度进行优化.本文综合考虑计算复杂度和捕获性能，建立联合优化因子y进行优化，其表达式为

式中，a、b为比例系数，按照实际需求调节合适的比例系数，建立联合计算复杂度和捕获性能优化捕获因子，其余仿真条件不变.

图3 给出了不同多普勒搜索间隔时联合优化因子y随分段数N、中频积累时间Ta的变化曲线.对比表3 和表4，可以看出：考虑计算复杂度的影响后，最小检测损耗变大，但计算复杂度下降；在多普勒搜索间隔fdΔ=2 000 Hz 时，检测损耗变大约1.7 dB，但计算复杂度减小了21.2%.

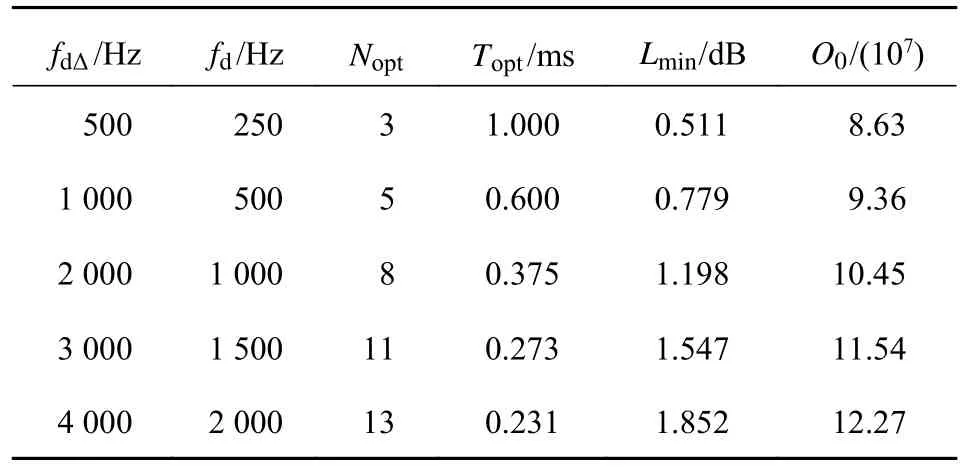
表3 不同多普勒搜索间隔下最优分段数N

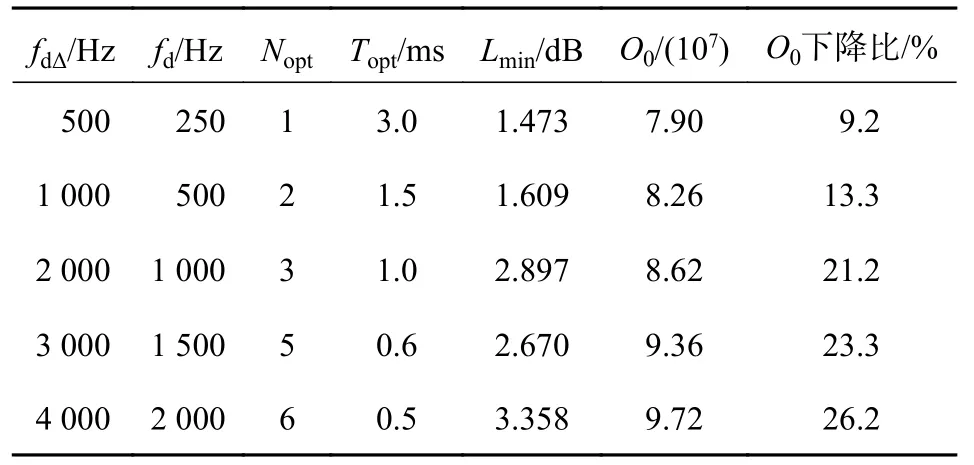
表4 不同多普勒搜索间隔联合下最优分段数N

图3 不同多普勒搜索间隔时y 随N 和Ta 的变化曲线

2.2 多普勒搜索间隔、相关器个数给定时的不同接收机灵敏度

对应不同接收机灵敏度的情况，即不同的信号CNR，设定总时间T为3 ms，码相位搜索间隔为0.5 个码片，多普勒搜索间隔fdΔ为1 000 Hz，每一段相关器个数M为8，改变输入CNR，分析检测损耗与分段数N之间的关系，同理可以确定两种优化方法的最优分段数、最小检测损耗和计算复杂度.

图4 给出了不同CNR 时检测损耗和联合优化因子y随分段数N的变化曲线.可以看出：在不同CNR情况下，两种优化方法均存在最优分段数；随着CNR变大，最优分段数Nopt也在变大；考虑计算复杂度后，联合最优分段数Nopt相比于单一捕获性能最优分段数变小，当CNR 为50 dB-Hz 时，联合最优分段数Nopt变为2，此时损耗增大约1 dB，计算复杂度下降约18%.

图4 不同CNR 时Lc 和y 随N 的变化曲线

2.3 多普勒搜索间隔、接收机灵敏度给定时的不同相关器个数

对应不同相关器个数M的情况下，设定总时间T为3 ms，码相位搜索间隔为0.5 个码片，多普勒搜索间隔fdΔ为1 000 Hz，输入CNR 为45 dB-Hz，分析在不同相关器个数M的情况下，检测损耗与分段数N之间的关系，同理可以确定两种优化方法的最优分段数、最小检测损耗和计算复杂度.

图5 给出了不同相关器个数时检测损耗和联合优化因子y随分段数N的变化曲线.可以看出：在不同的相关器个数M的情况下，两种优化方法均存在最优分段数，且最优分段数随着M变大而变小；考虑计算复杂度后，联合最优分段数N与单一捕获性能最优的分段数基本保持一致，在M为16 时联合最优分段数为4，此时损耗增大约0.3 dB，计算复杂度下降约4%.

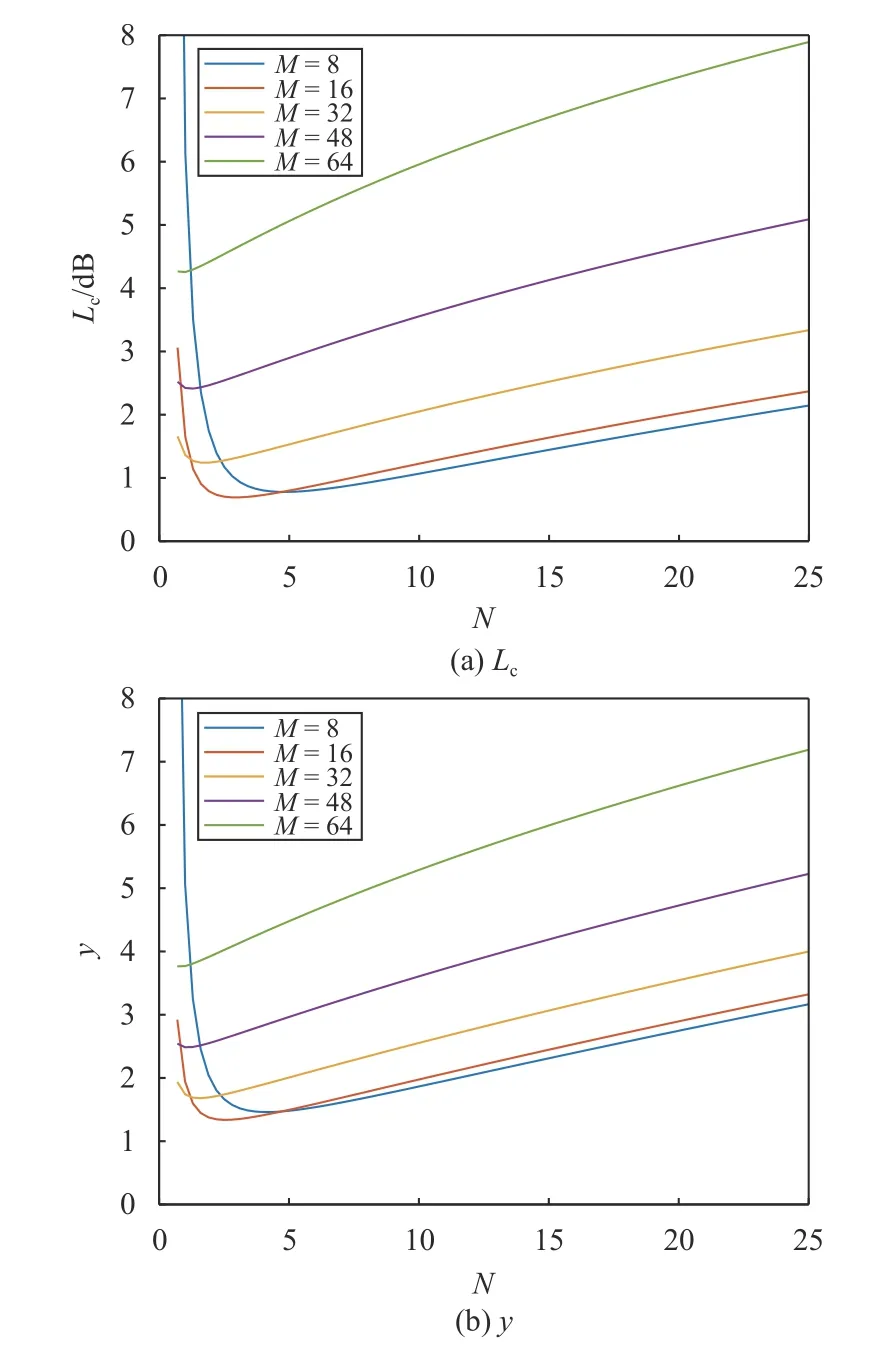
图5 不同相关器个数M 时Lc 和y 随N 的变化曲线

3 结束语

本文针对卫星导航尤其是短突发信号的捕获，提出了一种基于复杂度与性能联合优化的卫星导航信号捕获方法，采用并行频率搜索避免大规模点数的FFT 运算，详细推导了分段相关-视频积累捕获算法的捕获性能和计算复杂度，建立了联合优化因子.在不同多普勒搜索间隔、不同接收机灵敏度、不同相关器个数的情况下分别分析最优分段数，对比分析了捕获性能最优和联合最优的计算复杂度和捕获性能，仿真结果表明：

1)随着多普勒搜索间隔变大、信号CNR 变大，最优分段数也随之变大，最优中频积累时间变小，但相关器个数变大时，最优分段数变小，最优中频积累时间变大；

2)捕获性能和计算复杂度联合最优分段数相比于单一捕获性能最优分段数变小，在损失一定捕获性能的情况下可降低计算复杂度；

3)捕获性能和计算复杂度联合优化方法在不同多普勒搜索间隔、不同接收机灵敏度的情况时，相比于传统优化方法，计算复杂度下降明显，但在不同相关器个数情况时，两种优化方法结果基本保持一致.

本文可以为导航信号尤其是短突发信号的捕获提供优化策略，且对捕获算法计算复杂度的优化也有重要意义.