基于IRS辅助MIMO通信的双时间尺度信道估计
马诗婷
(南京邮电大学 通信与信息工程学院,江苏 南京 210003)
0 引言
多输入多输出(Multiple-Input Multiple-Output,MIMO)技术自提出以来一直在无线通信领域扮演着重要角色。然而,为降低硬件成本和能源消耗,未来需要更高能效的技术,因此智能反射面(Intelligent Reflecting Surface,IRS)以其低成本、低能耗的优势脱颖而出[1-3]。IRS 是由低成本的大型无源反射元件组成的平面,每个无源元件可以独立地反射接收到的信号并调整元件的相移,从而产生幅值和相移可重构的反射信号,以此增强有用信号或抑制干扰信号。然而,IRS 辅助通信的信道估计面临比传统通信场景信道估计更为严峻的挑战。这是由于大多数IRS 采用全被动元素,仅配备了简单的板载信号处理单元,只能反射电磁波,并不具备处理复杂信号的能力,难以获取信道状态信息(Channel State Information,CSI)。目前,大多数信道估计方法通过利用基站(Base Station,BS)和用户设备(User Equipment,UE)的有源收发器估计出BS、IRS 与UE 之间的级联信道,即BS-IRS-UE 级联信道[4-5]。尽管大多数预编码方案都是基于级联信道的知识,但存在一些预编码方案[6]需要BS-IRS 信道和IRS-UE 信道的单独CSI。更重要的是,级联信道估计方法的导频开销非常高,典型的IRS 辅助多用户无线通信系统配有大的BS 天线、IRS 元件和UE。高导频开销在实践中限制了频谱效率并导致信道估计延迟,而对于高移动无线通信,这个问题可能更加严重,因此研究可以在短相干时间内进行准确信道估计的方法十分必要。
1 相关研究
目前关于IRS 辅助无线通信的研究有很多,例如文献[6-11]均对联合优化BS 处的预编码矩阵和IRS 处的反射系数向量进行了研究,然而多用户MIMO 的预编码问题被证明是非凸的和NP-hard[9]的。因此,文献[10-11]试图为IRS 辅助的通信系统找到接近最优的联合波束成形解决方案。此外,文献[12-13]对IRS 辅助安全通信问题进行了探讨。然而,在众多相关研究中,针对IRS 辅助通信系统信道估计的研究还很有限。例如,文献[4]提出一个时隙只开启一个IRS 元件,成功地估计出IRS 元件的级联信道。由于其他IRS 元件不发射导频,因此信道估计精度会受到接收信噪比(Signal-To-Noise Ratio,SNR)下降的影响。文献[5]设计了一系列反射系数向量,并实现了级联信道的最小方差无偏(Minimum Variance Unbiased,MVU)估计,然而该方案的导频开销等于IRS 元件的数量乘以UE 的数量,限制了其在具有大量IRS 元件系统中的应用。文献[14]提出一种在IRS 辅助MISO 通信系统的场景下利用双时间尺度特性估计信道的方法,并显著降低了平均导频开销,但只考虑了UE 单天线的情况,有一定局限性。文献[15]提出一种巧妙的方法减少导频开销,首先估计一个UE 的级联信道,并将其作为参考信道,然后利用不同UE之间信道的相关性估计其他UE 的级联信道,但该方法在SNR 较低时信道估计不准确。文献[16-17]利用IRS 信道矩阵的低秩特性构造联合稀疏矩阵,并设计矩阵填充问题实现级联信道估计。文献[18]通过挖掘IRS 级联信道的结构化稀疏特征提升信道反馈性能,显著降低了信道估计开销。文献[19-20]使用深度学习技术解决信道估计问题。文献[21]利用毫米波下大规模阵列的信道稀疏性减少导频开销。文献[22-23]概述了IRS 辅助无线通信系统中信道估计的基本原理、解决方案和未来机会,并提出一种具有低导频开销的信道估计新方案。文献[24]研究了IRS 信道的单结构稀疏性,并提出一种降维信道反馈方案,该方案具有较低的信道反馈开销。
然而,以上文献中的方法仅适用于低秩或稀疏信道的特殊场景,且存在信道估计实现复杂度过高、准确性较差等问题。为此,本文提出一种基于IRS 辅助的多用户MIMO 上行无线通信的系统模型,利用信道的双时间尺度特性分别估计BS-IRS 和 IRS-UE 之间单独的信道状态信息。仿真结果显示,与多种已有方案相比,该方案降低了导频开销和归一化均方误差,具有一定优势。
2 系统模型
本文建立的 IRS 辅助的多用户MIMO 上行无线通信系统模型如图1 所示,其由一个具有N个反射元件的IRS、1个配备MR根天线的BS和K个配备MT根天线的UE 组成。上行链路BS接收到的信号表示为:
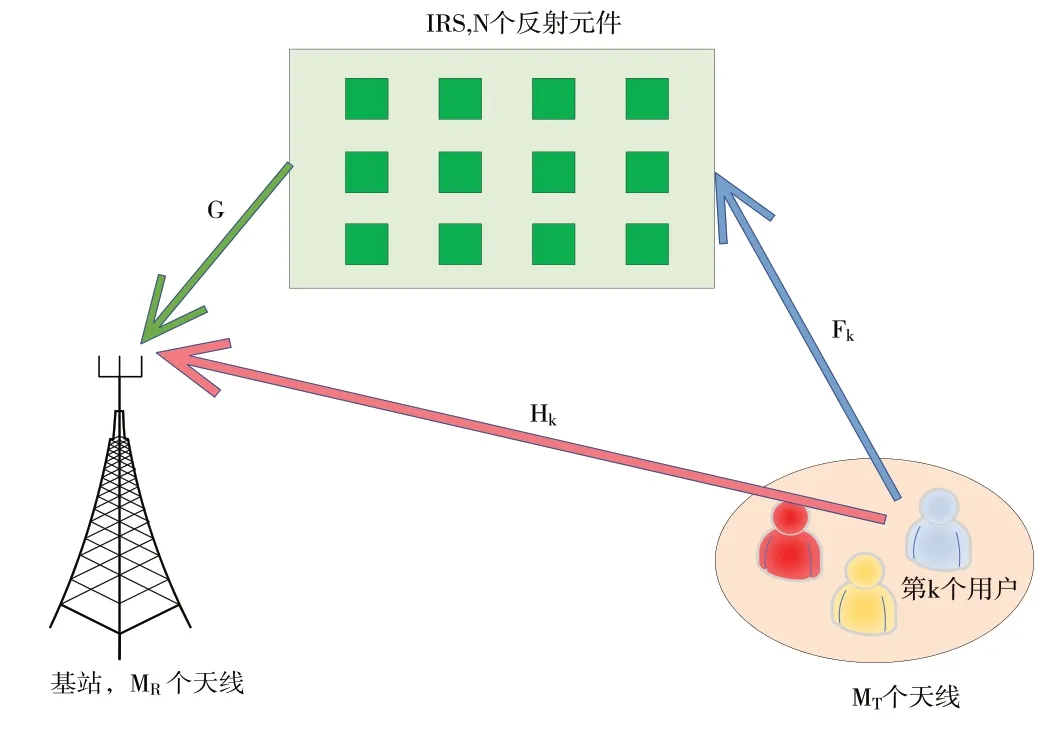
Fig.1 System model图1 系统模型
3 准静态BS-IRS信道估计
采用文献[14]中提出的基于坐标下降的信道估计算法估计准静态BS-IRS 信道。如图2 所示,在估计信道G时,传输帧由(N+1)个子帧组成,每个子帧持续L个时隙。在第t个子帧中,IRS 处的反射系数向量为。在第m1个时隙中,第m1根BS 天线发送一个非零导频,其余(MR-1)根BS 天线不发送导频。其余BS 天线接收到的导频可表示为:
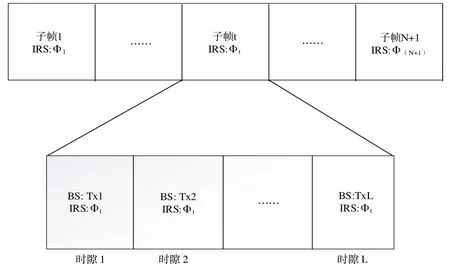
Fig.2 Large-timescale channel estimation frame structure图2 大时间尺度信道估计的帧结构
以下分3 个阶段估计准静态BS-IRS 信道。首先将问题划分为N个独立的子问题,每个子问题为估计BS 与单个IRS 元件之间的信道;其次估计每个子问题的初始值;最后,通过坐标下降法迭代优化对BS-IRS 信道进行估计。
首先将问题分为N个子问题,表示为:
分别通过求解N个子问题估计准静态BS-IRS 信道。对于给定的n,将第n个子问题表示为:
然后计算信道初始值,表示为:
最后利用坐标下降法迭代优化,在每i次外部迭代中,MR个信道的估计值都从第一个到最后一个进行迭代优化。第i次外部迭代信道估计值(具体证明详见文献[14])表示为:
4 移动IRS-UE和BS-UE信道估计
使用传统上行链路导频传输方案[5]估计移动IRS-UE和BS-UE 信道。如图3 所示,上行导频传输帧由τ0个子帧组成,每个子帧持续K个时隙。在第t个子帧中,IRS 处的反射系数向量为,反射系数向量的元素从{ +1,-1}中随机抽取。在一个子帧的K个时隙中,UE 发送上行导频序列,即,k=1,2,…,K。
为了区分来自不同UE 的导频,假设不同UE 发射正交导频序列,即:

Fig.3 The uplink channel estimation frame structure图3 上行链路信道估计的帧结构
在第t个子帧中,将多时隙导频传输模型表示为:
5 导频开销分析
在准静态信道估计中,BS-IRS 信道中有MRN个系数需要在大时间尺度上进行估计。本文使用(N+1)个子帧,每个子帧由L个时隙组成。为确保接收到的导频数大于信道系数数量,需要L≥2。相关导频开销为τ1=(N+1)L,与L成正比。在移动信道估计阶段,IRS-UE 信道中含有的NKMT个系数和BS-UE 信道中含有的MTKMR个系数均需在小时间尺度内估计。由于BS 在K个时隙的一个子帧中获得MRK个导频测量值,至少需要个子帧。因此,小时间尺度信道估计的导频开销为
在两次信道估计方案中,准静态BS-IRS 信道在大时间尺度上进行估计,因此需要根据BS-IRS 信道的估计频率计算平均导频开销。具体地,令TL和TS分别表示大时间尺度信道和小时间尺度信道的信道相干时间,并且TL=αTS且α≫1。在TS时间段内,平均导频开销计算为τ=当L=2 时,所需最小导频开销为
表1 为不同信道估计方案导频开销比较,其中:A 为本文方案;B 为采用级联信道的最小方差无偏估计方案[5];C为利用不同用户信道之间相关性进行估计的方案[15]。

Table 1 Pilot overhead comparison of different channel estimation schemes表1 不同信道估计方案导频开销比较
图4、图5、图6、图7 分别为导频开销与BS 天线数MR、IRS 元件数N、UE 数K、UE 天线数MT之间的关系,其中α=4。在图4 中,方案A 和方案C 的导频开销随着BS 天线数增加而下降,这是由于BS 可以在具有更多天线的时隙中获得更多上行链路导频测量值,而方案B 的导频开销与BS天线数无关。图5、图6、图7 结果表明IRS 元件数越多,UE越多,UE 天线数越多,需要的导频越多。可以看出,方案A的导频开销略低于方案C,显著低于方案B。
6 仿真结果与分析

Fig.4 Relationship between pilot overhead and MR(N=64,K=8,L=2,MT=2)图4 导频开销与BS天线数的关系(N=64,K=8,L=2,MT=2)
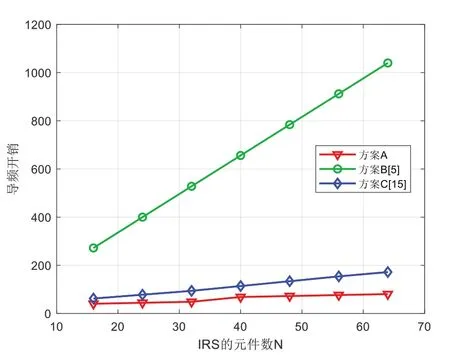
Fig.5 Relationship between pilot overhead and N(MR=32,K=8,L=2,MT=2 )图5 导频开销与IRS元件数的关系(MR=32,K=8,L=2,MT=2)
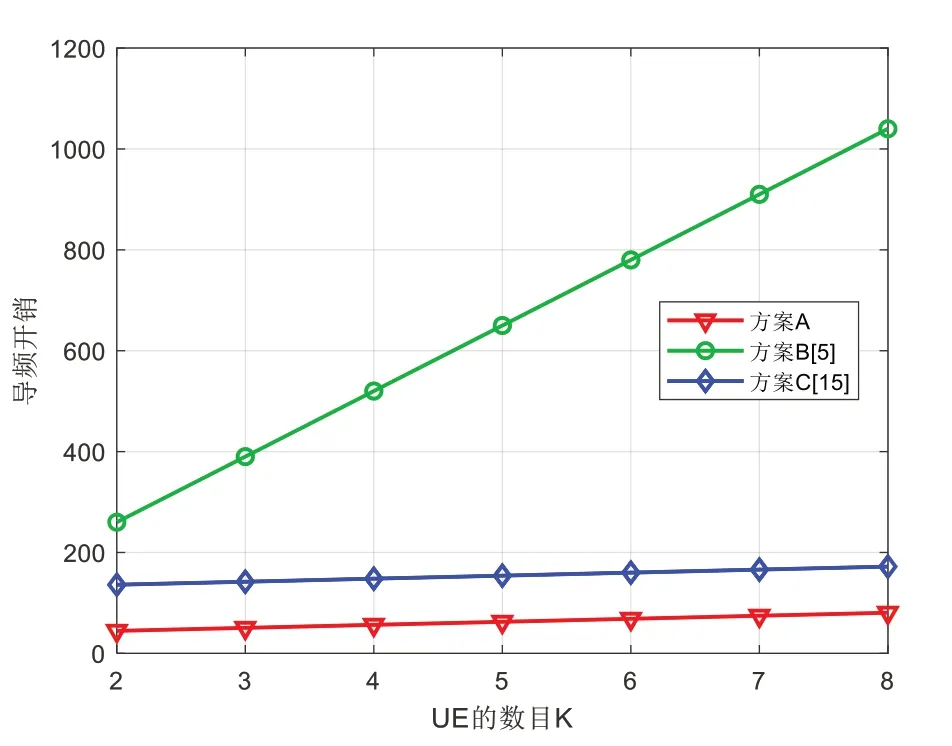
Fig.6 Relationship between pilot overhead and K(MR=32,N=64,L=2,MT=2)图6 导频开销与UE数的关系(MR=32,N=64,L=2,MT=2)
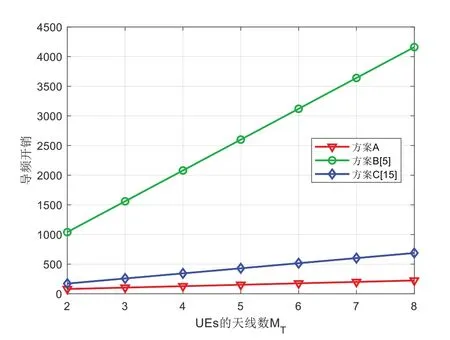
Fig.7 Relationship between pilot overhead and MT(MR=32,N=64,K=8,L=2)图7 导频开销与UE天线数的关系(MR=32,N=64,K=8,L=2)
对于大时间尺度信道估计中的双链路导频传输,将信干噪比定义为:
对于小时间尺度信道估计中的上行导频传输,将信噪比定义为:
NMSE 为归一化均方误差(Normalized Mean Square Error),用于评价预测值与实际值的拟合效果。其中,级联信道的NMSE 定义为:
直接信道的NMSE 定义为:
图8、图9 分别为级联信道和直接信道的NMSE 与上行SNRs的关系,可以看出二者的NMSE 均随SNR 的变大而降低,且方案A 的NMSE 比方案C 更低。虽然方案B 的信道估计更准确,但这主要是由于其导频开销比方案A 高出一个数量级。

Fig.8 Relationship between NMSE for the cascaded channel and uplink SNRs图8 级联信道的NMSE与上行SNRs的关系
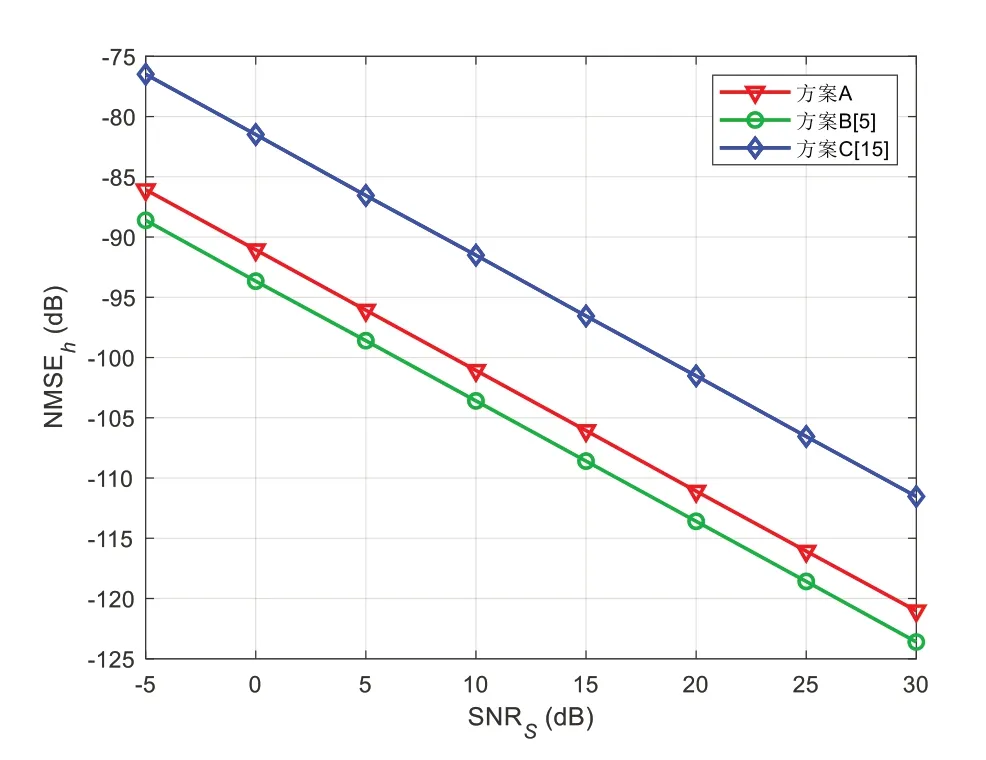
Fig.9 Relationship between NMSE for the direct channel and uplink SNRs图9 直接信道的NMSE与上行SNRs的关系
7 结语
本文提出IRS 在多用户MIMO 通信信道估计应用的新场景,利用信道的双时间尺度特性进行信道估计,分别通过基于坐标下降的信道估计算法和最小二乘算法估计BS-IRS 信道和IRS-UE 信道,在低导频开销的情况下实现了信道的准确估计。今后IRS 辅助通信的信道估计还可以扩展到更加丰富的场景,例如:①当使用多个IRS 辅助无线通信时,寻找一种低导频开销的信道估计方法;②当IRS 辅助高速移动的无线通信时,寻找一种传输协议进行信道估计并缓解多普勒频移。

