基于组合模型的天然气日负荷预测研究
邵必林,裴明洋,邓小玉
(西安建筑科技大学 管理学院,陕西 西安 710055)
0 引言
天然气作为一种清洁燃料,是我国实现碳达峰和碳中和的首选能源。精准的天然气日负荷预测不仅可以保障国民日常生活的稳定,而且在能源企业日常运维过程中也发挥着重要作用。随着城市的更新发展,当前形式对天然气调峰、管网的运维等提出了更高要求,天然气负荷预测成为能源系统面临的最棘手任务之一[1]。
刘春霞等[2]基于小波神经网络建立短期天然气负荷预测模型,并通过遗传算法优化预测模型的权值和阈值。张少平等[3]基于BP 神经网络建立短期天然气负荷预测模型,并以改进的粒子群算法优化预测模型的参数。两者都以神经网络为基础建立单一预测模型,但是基于单一模型的负荷预测无法捕捉负荷数据线性与非线性结合的特性,具有较大风险,因此组合模型与单一模型相比有一定优势。姜秋龙等[4]基于LSTM 和BP 神经网络建立两阶段预测模型,第一阶段用LSTM 进行初步预测,第二阶段用BP神经网络预测残差,最后将两阶段的预测值之和作为最终预测值,这种两阶段的预测模型易造成误差累积。为了克服单一模型的缺陷,Vinayak 等[5]提出4 种单一模型结合的组合模型,将单一模型预测的结果通过简单加权组成并联模型并验证了该模型的优越性。但是,简单的平均加权无法有效地分配各单一模型的贡献,采用群智能算法可使各单一模型的权重得到合理分配。
本文以民用天然气为对象,除考虑温度[6]、日期类型[7]、前一日负荷[8]和前两日负荷的影响外,还将引入舒适度和风寒系数[9]作为天然气负荷的影响因素,并验证了这两个指数与负荷存在较高的相关性。首先采用Elman神经网络和NARX 神经网络分别对天然气负荷进行预测,然后用改进的粒子群算法进行权重分配,将单一模型进行组合。基于实例分析表明,改进的粒子群算法性能优越,基于改进粒子群算法的组合预测模型精度高并且泛化能力较强,引进气象综合因子和前两日负荷的预测模型适用性更强。
1 模型建立
1.1 Pearson相关分析
Peasron 相关分析可以判断序列之间的相关程度,实现数据的降维和选优[10],相关系数的计算公式如下:
其中,R 表示影响因素a与b的Pearson 相关系数,和分别表示数据序列a和b的均值,ai和bi分别表示数据序列a和b的第i个数据,其中i=1,2,3,…,n。
本文选取平均温度[11]、风速和相对湿度[12]3 个气象因子进行可视化分析,它们与负荷的关系如图1—图3所示。
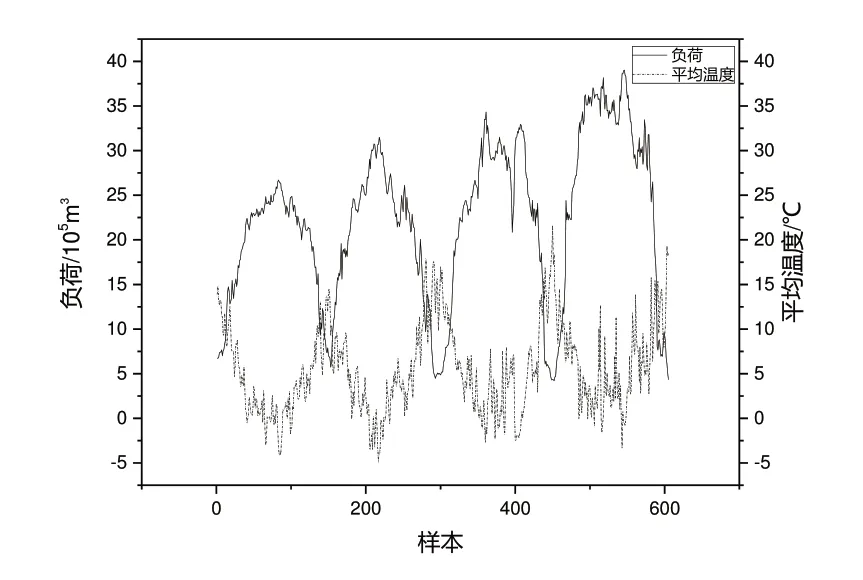
Fig.1 Variation relationship between temperature and load图1 温度与负荷的变化关系
由图1 可知,温度与负荷变化呈现出一定规律,负荷随温度的上升而下降,两者呈比较明显的负相关。由图2、图3 可知,风速和相对湿度与负荷的关系并不明显。对温度、风速和相对湿度与负荷进行相关性分析,结果如表1所示。
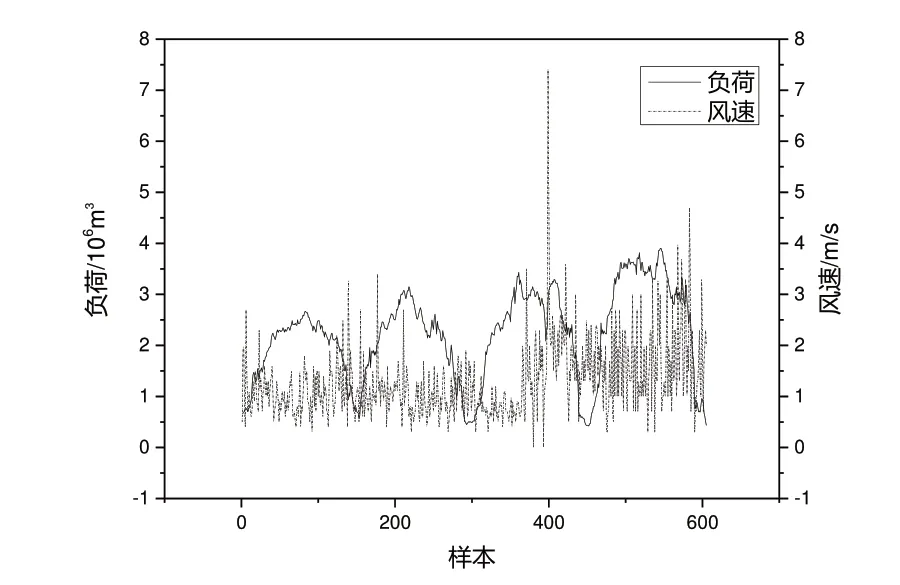
Fig.2 Variation relationship between wind speed and load图2 风速与负荷的变化关系
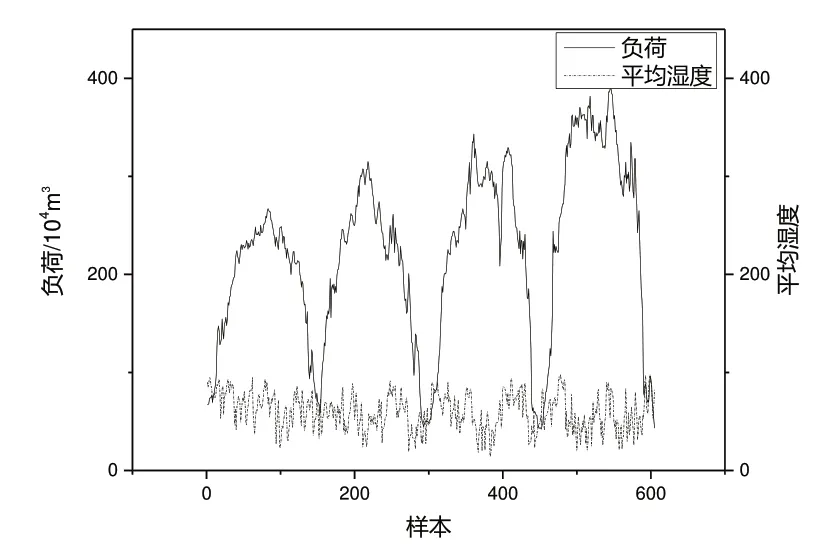
Fig.3 Variation relationship between relative humidity and load图3 相对湿度与负荷的变化关系

Table 1 Pearson correlation analysis results of daily natural gas load and influencing factors表1 天然气日负荷与影响因素的Pearson相关分析结果
由表1 可知,负荷与最高温度、最低温度和平均温度之间具有高度的负相关关系,其中与平均温度的相关性最高,负荷与风速和相对湿度的相关性微弱,但是风速和相对湿度会影响人体的舒适度,从而影响人们对天然气的使用。因此,本文引入舒适度指数和风寒指数两个气象综合因子作为负荷的影响因素。气象综合因子由多种气象因子综合而成,其中风寒指数综合了风速、气温和人体在舒适状态下的平均温度,舒适度指数综合了温度、风速和相对湿度。对舒适度指数和风寒指数与负荷进行相关性分析,结果如表2所示。

Table 2 Pearson correlation analysis results of daily natural gas load and meteorological integrated factors表2 天然气日负荷与气象综合因子的Pearson相关分析结果
由表2 可知,负荷与舒适度指数和风寒指数相关性显著,与舒适度指数具有负相关关系,与风寒指数具有正相关关系。由于人们的行为惯性,天然气日负荷也会受到历史负荷的影响,因此将前一负荷和前两日负荷也作为影响因素。此外,日期类型也会影响天然气的使用,因此将非工作日和工作日分别量化为0.7和0.5[13]。
1.2 Elman神经网络模型建立
Elman 神经网络是由输入层、隐含层、承接层和输出层组成的多层神经网络,与BP 神经网络[14]相比,增加了可以储存上一时刻历史信息的承接层,使网络处理动态信息的能力增强[15]。模型数学表达式为:
其中,x、l、y分别表示输入层、中间层以及输出层的节点向量,ly是承接层的反馈向量。w1、w2和w3分别表示输入层与中间层、承接层与中间层、中间层与输出层的连接权重。
模型构建主要包括以下几个要点的确定:输入、输出以及隐藏节点个数。Elman 神经网络参数设置如表3 所示,隐含层节点根据经验公式和试验确定。

Table 3 Parameter settings of Elman neural network表3 Elman神经网络参数设置
1.3 NARX神经网络模型建立
NARX 是一种动态神经网络,除输入层、隐含层和输出层外,还包含一个输入和输出的延迟层,同时网络具有反馈机制,使网络可以更生动地进行自适应调节[16]。模型数学表达式为:
其中,x(t)、y(t)分别表示神经网络的输入和输出,du和dv分别是输入和输出的最大延迟,f{·}为训练得到的网络结构。NARX 神经网络参数设置如表4 所示,隐含层节点根据经验公式和试验确定。

Table 4 Parameter settings of NARX neural network表4 NARX神经网络参数设置
1.4 TLPSO算法
1.4.1 标准粒子群算法改进
粒子群算法(Particle Swarm Optimization,PSO)是通过模拟鸟群觅食而产生的优化算法,其参数较少并且性能优越,在许多领域都有应用,但是其容易陷入局部最优值[17],并且在位移过程中没有考虑粒子间的关联性,但是多数文献只是提出了非线性惯性权重[18-21],考虑粒子间联系的相关研究较少。鉴于此,本文对标准粒子群算法进行改进:①提出随机惯性权重代替线性惯性权重;②将教学算法[18](Teaching Learning-based Optimization,TLBO)与粒子群算法相融合,引入教学思想,使粒子在每次迭代过程中兼顾其他粒子的位置,加强粒子间的联系,避免算法后期陷入局部最优。改进后算法(TLPSO)的速度更新公式和位置更新公式如下:
其中,w表示惯性权重;Vi,t和Xi,t分别表示粒子i在第t次迭代中的速度和位置;c1、c2表示常数;pbi和gbt分别表示单个粒子和整个粒子群搜索到的最优位置;pmt表示粒子群中所有粒子位置的平均值;r1、r2、r3、r4、r5表示[0,1]之间的随机数,round表示四舍五入函数。
TLPSO 的参数设置如表5所示。

Table 5 Parameter settings of TLPSO表5 TLPSO的参数设置
1.4.2 改进模型验证
为验证改进模型的有效性,选取5 个测试函数对改进前后算法性能作比较,分别为Griewank 函数(F1)、Sphere函数(F2)、Rastrigin 函数(F3)、Drop-wave 函数(F4)和Easom 函数(F5),测试函数具体情况如表6所示。

Table 6 Test function表6 测试函数
由表6 可知测试函数的维度、最优值和自变量范围。采用表6 的测试函数进行仿真实验,利用改进前后的算法分别寻优20 次,记录寻优结果并进行统计,分析对比两者的性能,结果如表7所示。
由表7 可知PSO 与TLPSO 的仿真及统计分析结果,与PSO 寻优结果相比,TLPSO 的20 次仿真最优值和平均值与目标值更为接近,平均绝对误差更小。除F4 函数外,TLPSO20 次仿真结果的方差也更小,表明改进算法的性能也更加稳定,对于F4 函数,PSO 的寻优值与目标值-1 差距过大,因此在5个测试函数的仿真上,TLPSO 的稳定性和寻优能力均优于PSO。通过仿真实验和分析表明,TLPSO 与PSO 相比在低维和高维都表现出更好的性能。
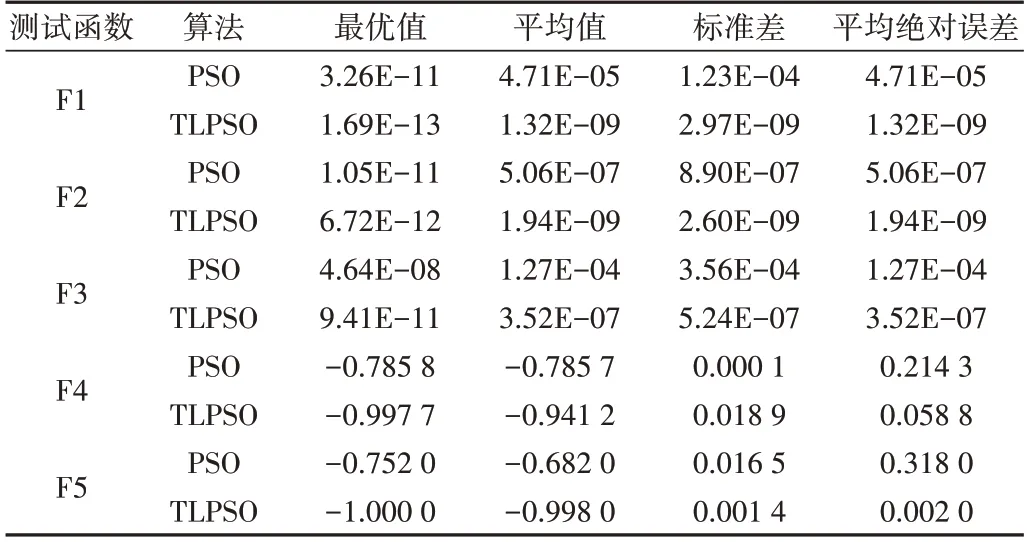
Table 7 PSO and TLPSO simulation and statistical analysis results表7 PSO与TLPSO仿真及统计分析结果
1.5 组合预测模型建立
选用前一日负荷、前两日负荷、最高气温、最低气温、平均气温、风寒指数、日期类型、舒适度指数和天然气负荷为Elman 神经网络和NARX 神经网络的输入,对未来天然气日负荷进行预测。
基于TLPSO 和并联神经网络的天然气日负荷预测流程如下:①收集天然气负荷及相关影响因素数据;②对异常数据作归一化处理;③划分训练集和测试集;④建立基于Elamn 神经网络和NARX 神经网络的天然气负荷预测模型;⑤建立TLPSO-Elamn-NARX 并联组合预测模型;⑥输出仿真结果并进行模型性能分析。
由于天然气负荷预测具有不确定性和复杂性,在使用单一模型进行预测时具有较大的风险性,即任何单一的预测模型在不同的情况下都不能取得令人满意的效果,因此并联组合模型在预测天然气负荷预测时有一定优势。天然气负荷并联组合预测是指在使用多个单一模型进行预测后,采用可靠的方法确定单一模型的权重,将各权重与对应模型的预测结果相乘并相加以提高预测精度。并联组合预测模型公式如下:
其中,f(x)为并联组合预测模型预测结果;g(xi)为第i个单一模型预测结果;wi为第i个单一模型权重,且w1+w2=1。
组合模型的均方误差(Mean-square Error,MSE)越小,表示组合模型预测性能越好,因此对组合模型的均方误差进行寻优并对Elman 神经网络模型和NARX 神经网络模型进行权重分配,TLPSO 的适应函数为:
其中,w1、w2分别为ELamn 神经网络模型和NARX 神经网络模型权重,MSEELman、MSENARX分别为ELamn 神经网络模型和NARX 神经网络模型的均方误差。
2 预测实例分析
本文选取西安市某气站连续4 年11 月到3 月日负荷数据进行仿真,以前574 个数据为训练集训练模型,后31个数据为测试集检验模型精度,将两组数据进行归一化处理以加快网络收敛速度。
本文采用平均绝对百分比误差(Mean Absolute Percent Error,MAPE)和平均绝对误差(Mean Absolute Error,MAE)作为验证组合模型预测效果的指标。
其中,et为t时刻预测值与实际值的差值,yt为t时刻的实际值,n为预测天数。为研究并联组合模型的性能,在只考虑气温和日期类型情况下进行实验仿真以对比TLPSOElamn-NARX 模型与两种单一模型、平均权重组合模型的误差指标。4种模型预测结果如图4所示。
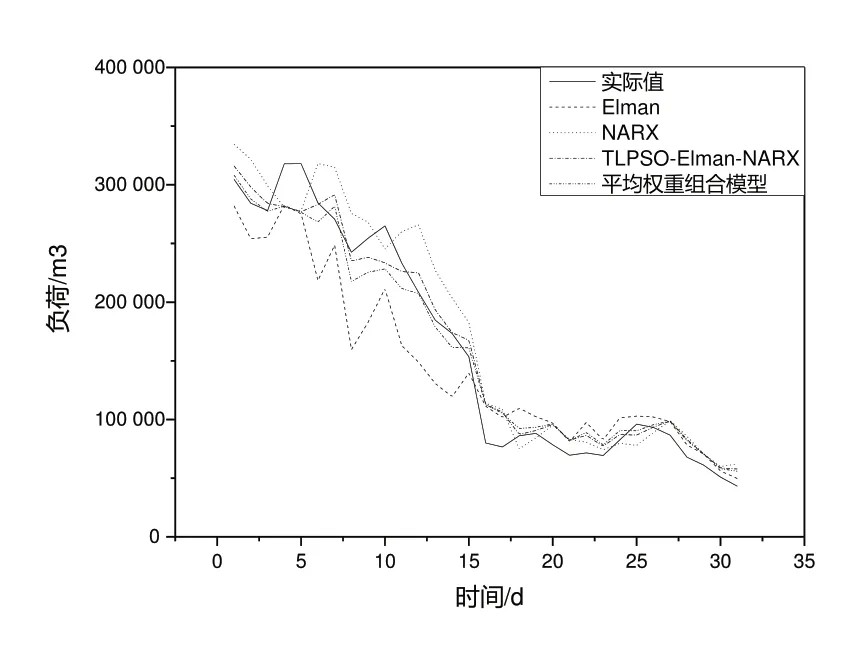
Fig.4 Prediction results of parallel combination model图4 并联组合模型预测结果
由图4 可知,TLPSO-Elamn-NARX 模型预测效果明显比Elamn、NARX 和平均权重组合模型更接近实际值。
为研究综合气象因子、前两日负荷对负荷预测精确度的重要贡献,采用控制变量法进行仿真,对比并联组合模型添加综合气象因子、前两日负荷前后的预测准确率,结果如图5和图6所示。
由图5、图6 可知,TLPSO-Elamn-NARX 模型在添加综合气象因子和前两日负荷后预测精度有显著提高,并且前两日负荷对预测精度的影响比综合气象因子更大。有无气象综合因子和前两日负荷模型预测效果评价指标如表8所示。
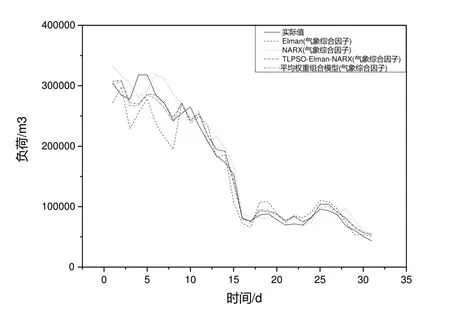
Fig.5 Prediction results with and without meteorological comprehensive factors图5 有无气象综合因子的预测结果
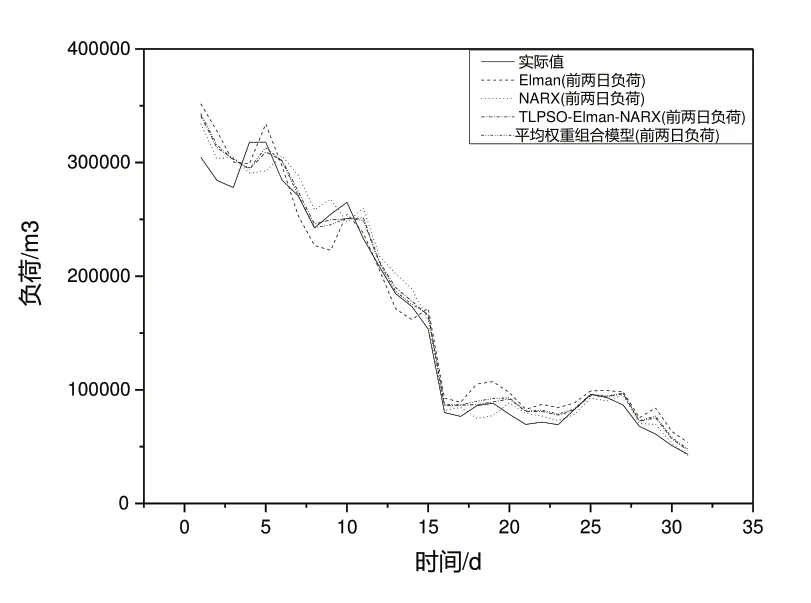
Fig.6 Prediction results with and without first two days' load图6 有无前两日负荷的预测结果
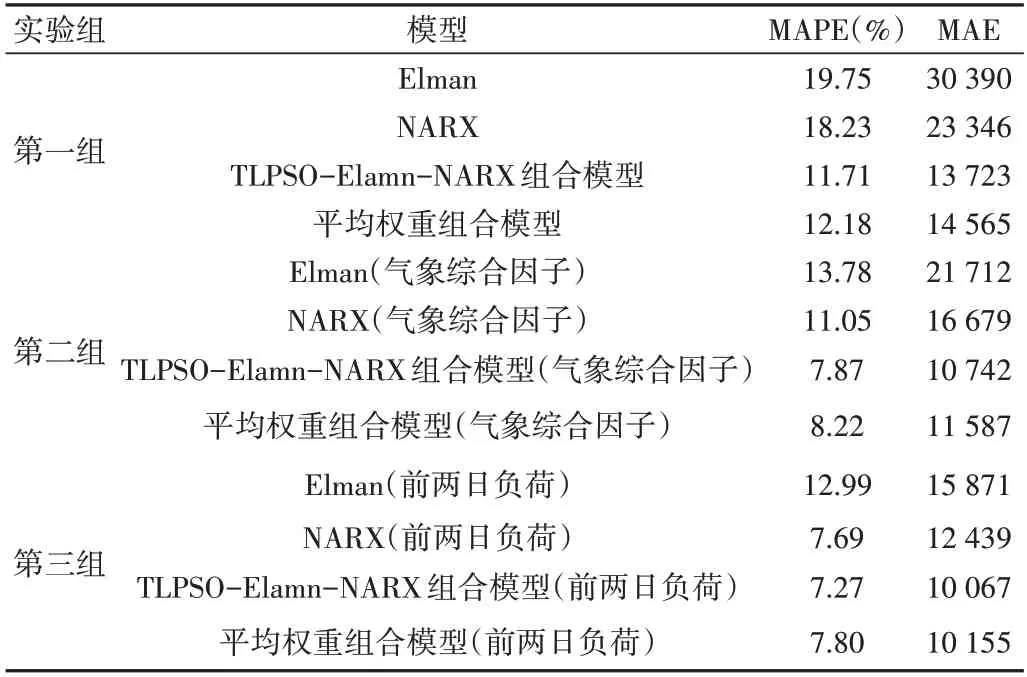
Table 8 Evaluation of prediction effect of models表8 模型预测效果评价
由表8 可知,第一组实验中,TLPSO-Elamn-NARX 组合模型的预测准确率高于单一模型和平均权重组合模型,相较于两个单一模型MAPE 和MAE 下降幅度较大,较平均组合模型MAPE 和MAE 分别降低0.47%和842,预测效果有较大提升。
第二组实验中,加入气象综合因子的模型MAPE、MAE 均有较大提升,表明气象综合因子可以有效提高预测模型精度。
第三组实验中,加入前两日负荷的模型MAPE、MAE均有较大提升,表明前两日负荷可以有效提高模型预测精度,并且前两日负荷对预测精度的影响比气象综合因子要大。但是平均权重组合模型的MAPE 未能降低,表明平均权重组合模型具有一定的局限性。
上述3 组实验结果表明,TLPSO-Elamn-NARX 组合模型可以将单一模型的优势组合起来,有效提高负荷预测精度,平均提升绝对误差百分比为3.03%。TLPSO 模型与单一模型和平均权重模型相比具有极大优越性。此外,多组仿真结果表明,所提模型结果与单一模型相比较为稳定,鲁棒性更好。
3 结语
针对天然气负荷预测精度不高、单一模型预测结果不稳定等问题,本文从影响因素和模型两个方面入手。对于影响因素,采用相关性分析剔除冗余的影响因素并引入气象综合因子,运用敏感性分析论证了分别加入气象综合因子和前两日后多种预测模型的性能。对于预测模型,提出了一种并联组合模型,采用TLPSO 分配Elman 神经网络模型和NARX 神经网络模型的权重。
实例分析表明,融入“教学思想”的随机权重粒子群算法在低维度和高维度搜索速度和精度都优于标准粒子群算法;加入气象综合因子后预测模型误差大幅降低,预测结果更加接近真实值,组合模型的性能优于单一模型和平均权重组合模型。所提出的方法不仅降低了预测误差,而且大幅度提高了稳定性,为天然气负荷预测提供了一种高效的方法,同时对提高天然气企业的管理效率具有借鉴价值。下一步研究将在现有组合模型基础上进行优化,寻找精度更高且结构更加简化的模型。

