改进麻雀搜索算法优化支持向量机的人脸识别

周凯莉，吴有超，姜元昊，周 枫

（1.江苏科技大学 计算机学院；2.江苏科技大学 机械学院，江苏 镇江 212003）

0 引言

目前成熟的人脸识别与分类算法有卷积神经网络（Convolutional Neural Network，CNN）［1］、特征脸方法（Eigenfaces）［2］、局部二元模式直方图（Local Binary Patterns，LBP）、改进的特征脸方法（Face Net）［3］、三维识别、主成分分析（Principal Component Analysis，PCA）［4］与支持向量机（Support Vector Machine，SVM）结合的内核方法等。内核方法首先从训练图像集的协方差矩阵中接收特征向量，计算每张图像的主要成分，然后将未知图像的主要成分与所有其他图像的成分进行比较。内核方法的重难点在于支持向量机进行图像识别分类时如何提高准确度。其中一种思路是采用智能算法优化支持向量机的核函数和惩罚参数，建立识别分类器应用于人脸识别特征分类。

将人脸识别用于身份认证具有重要的安全意义，因此目前市场对人脸识别技术的需求依然旺盛。本文基于内核方法，先使用主成分分析法对图片提取响应特征，提出加入自适应调整惯性权重策略［5］的改进麻雀搜索算法［6］与支持向量机融合（Improved Sparrow Search Algorithm-Support Vector Machine，ISSA-SVM）的人脸特征识别分类模型［7］。实验结果表明，该算法在人脸识别领域的应用具有理论可行性，为人脸识别相关算法的拓展提供了其他可行思路。

1 相关研究

群体智能算法是一个庞大的体系，已应用比较成熟的有遗传算法（Genetic Algorithm，GA）、蚁群算法（Ant Colony Algorithm，ACO）、灰狼算法（Grey Wolf Algorithm，GWO）、粒子群优化算法（Particle Swarm Optimization，PSO）等。麻雀搜索算法（Sparrow-Search-Algorithm，SSA）受到麻雀觅食行为和反捕食行为的启发而提出，属于智能仿生算法中粒子群优化算法（PSO）的其中一种，用于模拟群体智能所产生的一种进化计算技术（Evolutionary Computation）。相较于其他智能优化算法，麻雀搜索算法是一种高效、灵活、内存占用低、易于实现的搜索算法，适用于大规模搜索问题。

薛建凯［8］首次提出模拟麻雀觅食行为和预警行为的模拟优化算法，同时制定相应规则，再建立对应的数学模型，归纳了算法的实现步骤；冯璋［9］引入非线性收敛因子，利用动态权重调整适应度值改进灰狼算法，优化支持向量机的核函数和惩罚参数在人脸识别中的应用，实验结果表明，改进的灰狼算法分类器（Improved Grey Wolf Algorithm-Support Vector Machine，IGWO-SVM）最终识别准确率为88.3%；吴永红等［10］提出基于学习因子与惯性权重动态调整的粒子群算法优化支持向量机参数（Particle Swarm Optimization-Support Vector Machine，PSO-SVM），最终的识别准确率为81%；左建国［11］提出基于蜂群算法的选择性集成SVM 分类器进行人脸识别分类。但这些群智能仿生算法本身或经过优化后，仍会受限于自身弊端，即容易陷入局部最优问题。

2 麻雀搜索算法

2.1 原理介绍

麻雀搜索算法的基本思想是将搜索空间分成若干个子空间，然后对每个子空间进行搜索，直到找到目标或搜索空间为空为止。仿生算法是一种基于生物进化思想的算法，如粒子群算法PSO 通过模拟生物进化过程，逐步优化解法，最终找到最优解［12-13］。麻雀搜索算法更加注重局部最优解，在一定程度上克服了PSO 算法的局限性。

麻雀是一种小型鸟类的统称，通常少则十几只，多则几十只聚集在一起。规定由N 只麻雀组成的种群表示形式如式（1）所示。该麻雀种群中每只麻雀可能有3 种行为：一是作为种群中负责搜索食物的发现者；二是作为加入发现者的跟随者，向发现者的位置移动觅食；三是警戒侦查者，当警戒麻雀发现危险，立即发出鸣叫。其中，发现者与跟随者的行为身份是可以动态转变的，但总体比例不变。当警戒侦察者发出鸣叫，跟随者向安全区域散开，群体中间的发现者随机走动，向安全区的跟随者靠近。

2.2 发现者位置更新

SSA 中的发现者为群体搜索食物，每个发现者都有一个适应度值，值越高找到食物的几率越大，其带动跟随者进行种群移动。在每次迭代过程中，发现者位置公式的更新如式（2）所示。

式中，参数t为当前迭代次数，itermax为最大迭代次数，Xij是第t次迭代时第i只麻雀个体在第j维中的位置信息，α为(0，1)区间上的随机数，L为每个因子均为1 的一个l×d的矩阵，Q是服从标准高斯分布的随机变量的一个样本，R2为警戒者发出的预警值，R2∈(0，1)。ST为预警安全值，ST∈(0.5，1)。若R2＜ST，表明未发现捕食者，种群状态安全；若R2≥ ST，表示部分个体发现或遭遇捕食者，所有麻雀响应危险警报，需要快速飞到其他安全区域。根据公式（2）可知，下次迭代过程中的发现者围绕当前位置移动。移动位置值的变化范围Y如式（3）所示。

2.3 跟随者位置更新

在每次迭代中，跟随者位置更新如式（4）所示。

2.4 预警行为

群体中的所有麻雀都具有相同的预警机制，该机制可理解为，一群麻雀觅食过程中有约10%-30%的麻雀意识到有捕食者，从而触发报警机制。警戒者的位置更新如式（5）所示。

上述公式中，k为随机数，k∈[-1，1]；β为随机步长控制系数，服从方差为1、均值为0 的高斯分布［14］；fi表示第i个麻雀个体的适应度值；fg代表当前最佳适应度值；fw表示当前最糟糕的适应度值；ε 表示最小的参数，以避免分母为零。当fi＞fg，意味着个体处于群体边缘；当fi=fg，表明在群体中间的麻雀意识到了危险，需要散开飞向安全的地方。

3 改进麻雀搜索算法

麻雀搜索算法需要克服的问题是平衡局部搜索与全局搜索，尽量避免陷入局部最优。采取如下所述的优化策略：

3.1 Tent混沌映射

目前，群体智能算法初始种群个体的生成是在给定范围内随机生成数组，导致初始个体具有较大的随机性和不确定性，算法效果不佳。因此，可以通过改进初始化种群的方式改进算法的优化和收敛性能，提升局部探索能力与全局探索能力。常见的混沌映射函数有Chebyshev、Circle、Gauss、Iterative、Logistic、Piecewise、Sine、Singer、Sinusoidal、Tent 等。图1 给出了这些混沌映射函数在参数区间［0，1］上的分布情况。

观察图1，对比其他函数，发现Tent 产生的混沌序列具有良好的分布性和随机性。将Tent 映射用到群智能优化算法中，选择多个不同的初始值，能产生稳定分布的混沌序列。为保证初始种群个体的自随机性，采取Tent 映射初始化麻雀种群来增加多样性，提高ISSA 算法的收敛速度。Tent 映射混沌的表达式如式（6）所示，经过伯努变换产生表达式如（7）所示。

3.2 自适应调整惯性权重策略

第i只麻雀在j维上的搜索能力如（8）所示。

其中，Xij是第i只麻雀位置在第j维上的分量，x*表示第i个麻雀移动过程最好位置的第j维分量，Xbest是全局最好位置的第j维分量，ε 是一个很小的正常数。由式（8）可推出：若Xij距x*较远，而x*距Xbest较近，则ISA 的值较大，此时全局搜索能力较强，应该适当减小惯性权重，增强局部搜索能力。反之，则应增大惯性权重。自适应调整惯性权重策略公式如（9）所示。

其中，α∈（0，1］，为控制惯性权重变化速度的参数。实验结果表明，当α=0.3 时，算法性能最佳，因此取α为常量0.3。

式（2）中引入自适应惯量，重新更新发现者所在位置，改进后的公式如（10）所示。

3.3 算法停滞问题

算法后期随着不断迭代，种群多样性丧失，导致过早收敛。一般引入柯西分布或高斯分布作为变异步长，解决算法停滞问题。图2 对比了标准高斯分布和标准柯西分布的概率密度函数曲线。图中显示，高斯分布峰值最高，两边走势陡峭。柯西分布的峰值比高斯分布低，速度走势更平缓。因此，高斯分布局部性强，容易得到局部最优解；而柯西分布全局性强，容易跳出局部最优解。

采用柯西变异来增加种群的多样性，可以适当提高算法的全局搜索能力，增加搜索空间。首先引入柯西变异公式，如式（11）所示。

其次，采用非线性动态递减权值策略，提高算法性能，如式（12）所示。r在区间［0，a］内随迭代次数非线性递减，t为迭代次数，k为调节系数，设置k与a都为常量1。

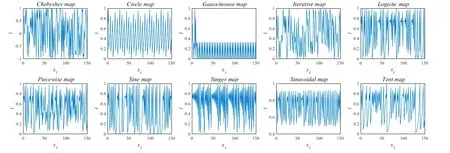
Fig.1 Chaotic function distribution图1 混沌函数分布图

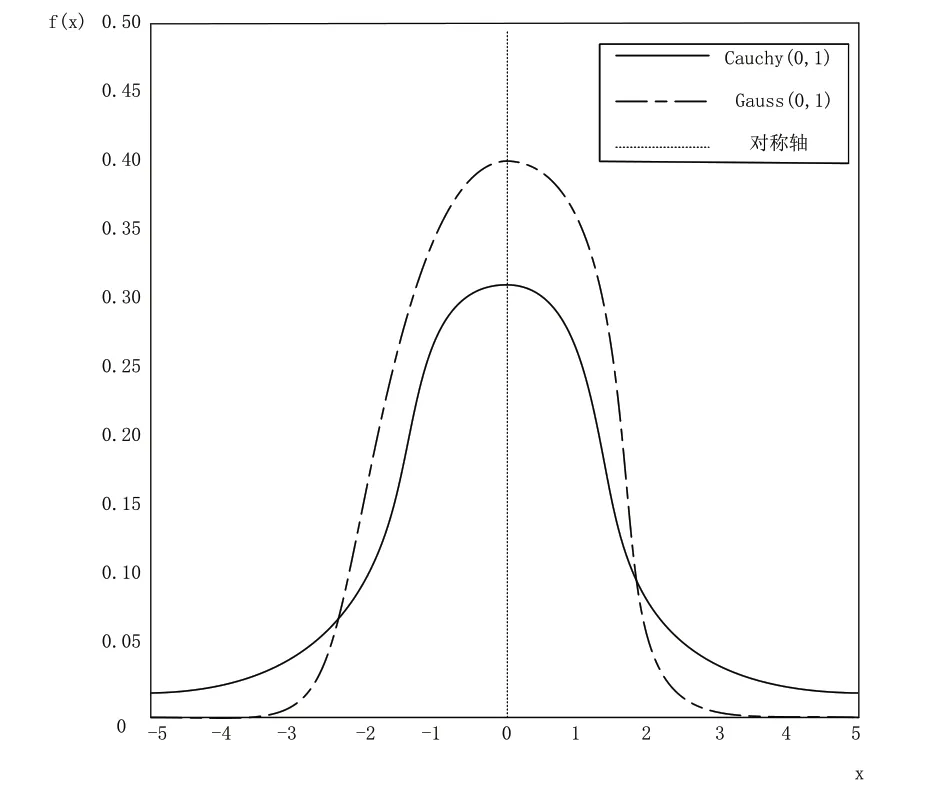
Fig.2 Probability density function curve of standard Gaussian distribution and the Cauchy distribution图2 标准高斯分布与柯西分布的概率密度函数曲线

δ 为麻雀的聚集度，h 为控制因子，自适应调整聚集度δ的大小，聚集度函数如式（13）所示。

选择当前适应度最佳的个体进行混合变异，变异公式如（14）所示。

4 SVM参数优化

4.1 支持向量机

支持向量机（SVM）是目前广泛研究与使用的分类算法，其核心思想是从输入空间向高维空间作映射，找到合适的最优分类超平面，实现对样本的分类。将其转化为需要解决的实际问题后可描述为：使最近样本到决策边界最大化。SVM 的推导优化目标函数如式（15）所示，其约束函数为yi(wTΦ(xi) +b) ≥1。将求最大值问题转换为求极限值问题，用拉格朗日乘子进行求解。

在实际环境中，存在少量异常分布样本。为允许异常样本存在，引入松弛因子ξ，使每个样本都有对应的松弛变量，引入松弛变量后的间隔问题称为软间隔。在式（15）的约束条件中加入松弛因子后的推导式如式（16）所示。当c趋于很大时，意味着分类严格，不能有错误；当c趋于很小时，意味着可以容忍更大的错误，且c是需要根据具体应用场景指定的一个参数。

Φ(x)是一种变换方法，即核函数变换。当数据集不是线性可分时，需利用核函数将数据集映射到高维空间，使得数据在高维空间中线性可分。高斯核函数RBF 是最常用的一种核函数，定义如式（17）所示。其中，σ 为核函数参数，用于控制高斯核函数的局部径向作用范围。当σ值很大时，样本分布更分散；当σ 趋于很小时，样本密度更集中，从而导致过拟合问题。所以，SVM 模型中的重点就是要选取合适的核函数参数。

4.2 参数优化

综上，首先需要找到最优的惩罚因子c 和核函数参数σ。将c 和σ 一起［18］组成麻雀种群初始化值（ci，σi），不断迭代整个算法，最终得到麻雀的最佳位置，即取得最优解，用于初始化麻雀算法和SVM 参数。

然后计算适应度值，将最优解保留。将特征选择最终转化为二元优化问题，优化后的特征选择结果用0 和1 表示，未选择该特征结果为0，选择该特征结果为1。在算法迭代过程中，使用适应度函数计算值评估解的质量，对ISSA-SVM 分类器所得到的最优解进行分类，根据其分类准确率与特征选择所选特征子集个数设计适应度函数，如式（18）所示。

其中，a［p（train）］、a［p（test）］为训练集和测试集（验证集）准确率，根据自身需要可选择只用训练集准确率或综合考虑验证集准确率。选择的特征个数为r，总特征个数为N，得到的适应度值为f，可使整个ISSA-SVM 分类器性能最佳。

4.3 样本判别

算法改进了SVM 的分类方法，在选取支持向量并得到最优分类超平面后，正类样本集和负类样本集均按各样本与分类超平面间的距离进行内部排序。随后将正类样本集内的中位数与负类样本集内的最大数分别定义为人脸相似度为100%和0%的端点值，每当处理需判断的新样本时，根据其与分类面的位置及距离得到其人脸相似度值。此时，距离超出100%和0%端点值的点将直接按端点值数据进行处理。接下来，改进麻雀算法将自适应地调整人脸相似度的接受阈值，以实现错误分类率这一评价指标数值的最小化。出于可视化目的，图3 展示了这一判别思想在

二维平面上的一个例子。

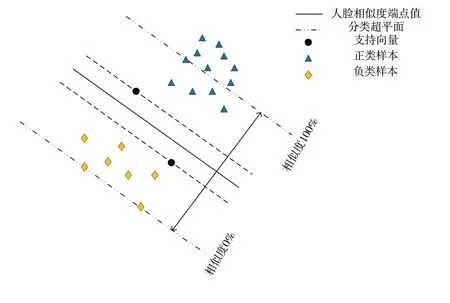
Fig.3 Face similarity value schematic图3 人脸相似度值示意图

4.4 人脸特征识别分类流程

麻雀搜索算法是一种基于群体智能的搜索算法，将改进的麻雀搜索算法用于解决优化问题，并将其与识别向量机结合，用于人脸识别。图4 描述了该过程的算法流程。

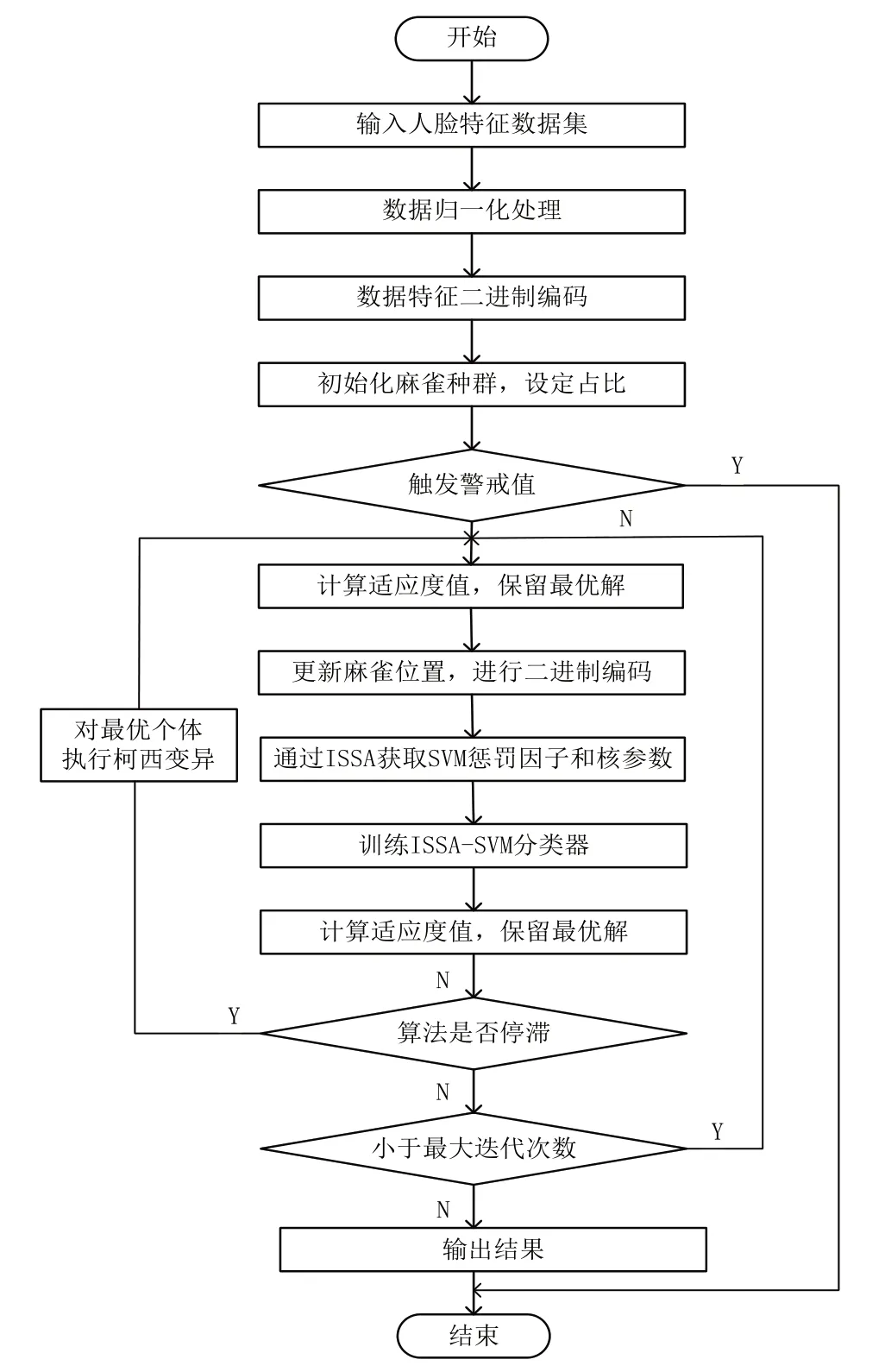
Fig.4 ISSA-SVM algorithm flow图4 ISSA-SVM 算法流程

5 仿真与实验

5.1 实验环境与条件假设

选择文献［6］和文献［7］所述算法进行对比仿真实验。实验环境如下：Windows10 64 位，处理器Intel（R）Core（TM）i7-8265U，主频2.2 GHz，内存16GB；仿真软件Matlab2021a。

为验证本文使用Tent 映射改进的麻雀搜索算法ISSA具有较强的稳定性，选择传统的麻雀搜索算法SSA 进行对比实验。遵循公平性原则，相关参数与迭代次数均保持一致。种群规模为100，安全值为0.8，发现者与跟随者的比例分别为0.3、0.2，最大迭代次数为500。

图5 为两个算法部分收敛曲线的对比图，水平方向代表迭代次数，垂直方向的坐标是一个越小越好的评价量，表示错误分辨率。传统麻雀搜索算法在迭代次数达到400次时，错误分辨率从43%左右降到约3%，开始逐渐收敛，而改进后的麻雀搜索算法在200 次左右即趋于收敛，收敛速度明显提高，错误分辨率为1.5%。

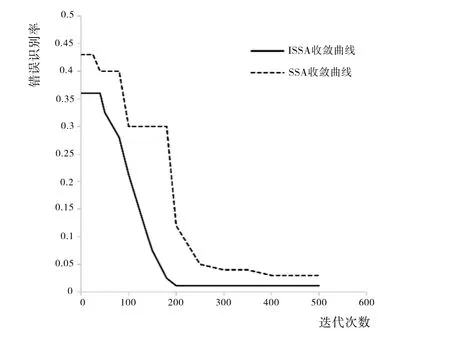
Fig.5 Comparison of convergence curve图5 收敛曲线对比

5.2 实验过程

采用某公司提供的人脸特征库进行实验，选取总样本数量672 个，分为训练集和测试集。取其中538 组作为训练样本，134组作为测试样本。ISSA-SVM 模型训练集样本分类结果如图6 所示，测试集样本分类结果如图7 所示。由图6 得出，训练集样本分类全部正确，其中0～269 组样本单调递增。测试集样本分类图中，两个样本分类错误，整体分类识别正确率为98.5%。

实验过程中，SSA 算法与ISSA 算法具有相同的输入数据、环境、优化SVM 惩罚因子c 和核函数参数σ。一旦确定这两个参数的最优值，将不会随着迭代动态更新。将SVM分类器、使用麻雀搜索算法优化SVM 的分类器（SSASVM）以及使用本文改进的麻雀搜索算法优化SVM 的分类器（ISSA-SVM）进行20 次实验，给出3 个算法的平均耗时。耗时记录如表1所示。

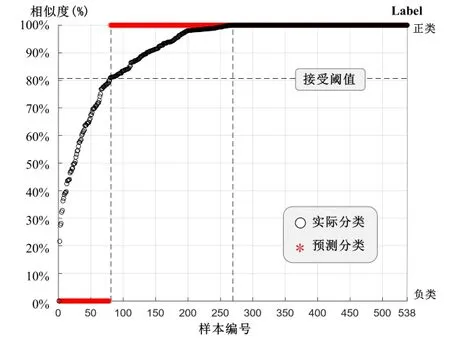
Fig.6 Training set sample classification diagram图6 训练集样本分类图

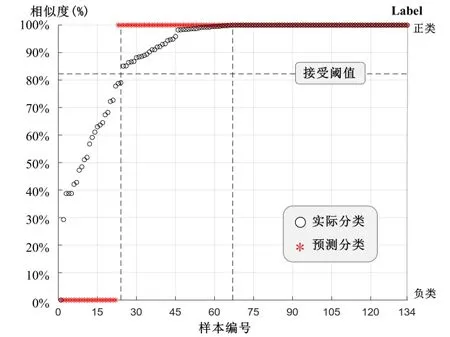
Fig.7 Testing set sample classification diagram图7 测试集样本分类图

Table 1 Comparison of average time consumption表1 平均耗时比较

结果显示，不管是未经改进的SSA 还是改进后的ISSA，其改变核参数与惩罚因子，与默认SVM 分类器的平均耗时仅相差0.000 095s，不会影响参数优化的效果和性能。

共实验20 次，与文献［9］中EGWO-SVM、文献［10］中PSO-SVM 算法给出的数据进行对比，给出SVM 的惩罚因子与核参数的解，优化参数比较如表2 所示。结果表明，ISSA-SVM 分类器对于人脸特征识别具有较好的稳定性。

在表2 的支持向量机参数基础上继续进行实验，最后得出不同优化算法分类器的训练集准确率、测试集准确率以及最终准确率。表3 列出了上述3 种识别方法的识别率对比结果。

Table 2 Optimized SVM parameters comparison表2 优化SVM参数比较

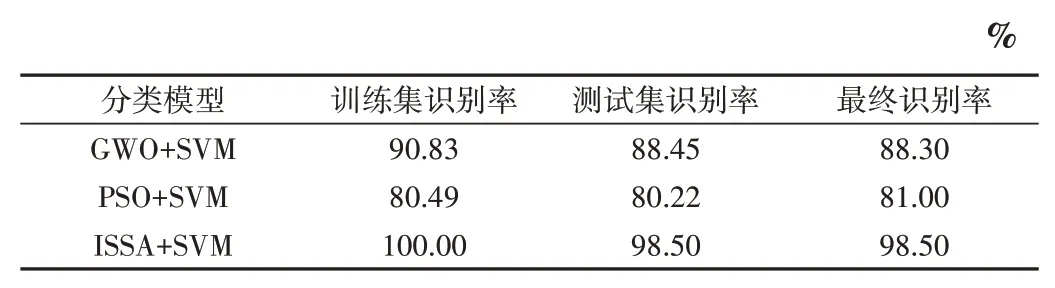
Table 3 Comparison of identification rate表3 识别率比较

5.3 结果分析

通过将本文优化的麻雀搜索算法ISSA 与传统麻雀搜索算法进行比较，表明ISSA 具有更高的准确性、更短的算法耗时和更广泛的适用性。将改进后的麻雀搜索与支持向量机相结合，优化惩罚因子与核参数，将文献［9］和文献［10］给出的算法结果与本文提出的分类模型进行比较，结果显示，ISSA-SVM 分类器在人脸特征识别方面具有较高的识别率和稳定性。

6 结语

将人脸识别用于身份认证对于安全保障具有重要意义，是值得研究的技术方向。本文提出一种基于改进麻雀搜索算法与支持向量机融合的人脸特征识别分类方法，新颖、简单、实用性强。实验结果证明，本文提出的ISSASVM 分类器在人脸特征识别分类方面的应用具有可行性。但是优化SVM 惩罚因子c 和核函数参数σ 后，这两个参数的最优值一旦确定，是不会随着迭代动态更新的。接下来的研究内容是算法如何在运行状态也能更新SVM 参数值，实现动态更新。同时使用该算法实现人脸识别模块，通过刷脸验证身份，做好信息加密，做到标准化、规范化。