6-DOF混联采茶机器人机构设计与动平衡分析
沈惠平 吉恩成 丁文芹 邓嘉鸣 华 耀 李 涛
(1.常州大学现代机构学研究中心, 常州 213164; 2.农业农村部南京农业机械化研究所, 南京 210014)
0 引言
2020年我国以水果、茶叶等为主的种植面积约1.7×108hm2,产量达2.6×108t,占全球果、茶产量的50%,成为世界第一的果(苹果、梨等)、茶等特经作物生产大国。其中,果、茶等生长的丘陵山区所占耕地比例在60%以上,且果、茶园地势不平坦,田间情况比较复杂。采摘机器人不仅可解决收获环节的劳动力替代问题,而且可保证采摘的效率与质量。
国内外学者已研究了一些采茶机器人及其技术。杜岳峰等[1]分析了农业机械智能化设计技术;顾宝兴等[2]研发设计了一种智能移动水果采摘机器人,它主要由智能移动平台、采摘机械臂、末端执行器、横向滑移机构和控制系统组成;秦广明等[3]设计了一种由茶叶图像摄取识别装置、控制电路板、智能采茶机器手、茶叶回收装置等组成的自走式智能田间采茶机器人;范元瑞[4]设计了一种Delta并联式自动采茶机,它安装于履带底盘小车,通过视觉相机识别适采叶芽并确定采摘点,以能耗为指标,利用Lamé曲线和Bézier曲线对轨迹规划曲线进行参数优化;尚凯歌[5]设计一种具有选择性采摘的名优茶采摘机器人设计方案,对其机械结构设计和运动学进行分析,并进行控制系统设计;WANG等[6]设计了一种由四轮独立转向、5自由度收获、导航和双目立体视觉系统组成的番茄采摘机器人,提升了采摘效率和精度;周天娟等[7]分析了设计果蔬采摘机器人需解决的主要问题是识别和定位果实,在不损害果实植株的条件下,按照一定的标准完成果蔬的收获。傅隆生等[8]研究了棚架式栽培模式自然生长条件下簇生猕猴桃无损采摘机器人末端执行器;周增产等[9]发明了移动式黄瓜收获机器人样机,该样机由行走车、机械手、视觉系统和末梢执行器组成;高凤[10]设计了采茶机器人的并联机构和末端执行器,并对其进行了运动学分析;陆怀民[11]研制了林木球果采集机器人,该机器人采用履带式拖拉机作行走机构,上部安装6自由度机械手,提升了采摘效率,降低了作业难度;HAYASHI等[12]发明了由圆柱形机械手、末端执行器、机器视觉单元、存储单元和移动单元组成的草莓收获机器人,可大幅提升采摘成功率;ARMADA等[13]设计一个用于水果采摘和搬运板条箱的完全自主机器人;卢伟等[14]设计了新颖的柑橘采摘机械手和末端执行器,并进行了运动学分析及仿真;高浩等[15]设计一种猕猴桃采摘机构,具有识别、夹持和扭转的功能。
在机构优化设计方面,叶柳等[16]以机构最大高度、急回特性和最大加速度为优化目标,使用惩罚函数和复合形法相结合的优化算法对六连杆冷温锻压力机传动机构进行尺寸优化;吕明青等[17]以滑块速度波动、压力角、侧向力和机构机械增益为优化性能指标,通过统一量纲和线性加权的方式构造出反映综合性能的多目标优化函数,采用遗传算法对六连杆传动机构进行了多目标优化设计。
综上可知,目前对用于非结构环境下精准采摘用6-DOF混联采茶机构的研究还较少。本文设计一种6-DOF混联采茶机器人,可用于茶园内任意位姿的茶叶采摘;对其进行运动学分析和机构杆长的尺寸优化,并利用有限位置法对其进行摆动力完全平衡设计;用遗传算法对该机构进行部分平衡优化。同时,分别验证摆动力完全平衡设计的正确性,以及部分平衡优化的良好结果。
1 6-DOF混联采茶机构设计与位置分析
1.1 机构描述
根据基于方位特征(POC)的机器人机构拓扑结构设计理论[18],设计一个6自由度的混联操作手[19],如图1所示。

图1 6-DOF混联采茶操作手
其中,机构串联部分包括:水平横梁通过两端移动副P1悬挂在固定于机架的两平行导轨上,设定静坐标系原点O固定在平行导轨末端,可作前后移动(X方向);通过移动副P2悬挂于水平横梁可作左右移动(Y方向);构件的上端通过移动副P3与铅垂梁连接,可作上下移动(Z方向);铅垂动臂的上端通过转动副R5与铅垂梁的下端连接,从而可绕铅垂梁的轴线转动(γ)。这样,串联机构部分可实现三平移一转动(X-Y-Z-γ)的独立运动。
机构并联部分包括:铅垂动臂的下端通过转动副R0与平面四杆机构(即:R1‖R2‖R3‖R4)的底边构件6连接,即平面四杆机构整体可绕铅垂动臂上的转动副R0轴线转动;构件6的左端通过联轴器与电机连接,而电机安装于铅垂动臂的支承板上,构件2上安装手抓。这样,手抓可实现绕转动副R0的转动β和绕R2轴线的转动α。
于是,6-DOF混联操作手可实现三平移三转动(3T3R)的输出运动(X-Y-Z-γ+α-β)。
该6-DOF混联采茶机器人将安装于如图2所示的移动底盘正下方。已研制完成的移动底盘允许串联模组负责大范围内运动,其中X、Y、Z方向移动的最大距离分别为600、800、200 mm,绕Z轴转动的角度可达360°;而并联部分转动角β可在[0°, 300°]之间变化,α可在[0°, 45°]之间变化。因此,该6-DOF混联采茶机器人可对茶叶任意位姿进行采摘。

图2 安装6-DOF混联采茶机器人的行走移动底盘
图2为履带式多动能机架样机,混联操作手悬挂于其正下方,其工作原理为:当行走的移动底盘移动到一片采茶区域时,采茶机器人末端的摄像头(安装在采茶剪刀的附近)识别出茶叶的位置与姿态,其信号反馈给控制系统,赋予6个伺服电机开始运动,从而使采茶剪刀能以任意姿态到达茶园空间任意位置的茶根部进行精准采摘。
1.2 机构位置分析
6-DOF混联采茶机器人机构的坐标系建立及各参数标注,如图3所示,其中,并联部分的lFH=l1、lHJ=l2、lJG=l3、lFG=l4、lHP=l′1;串联部分的横向导轨长度lAB=l7、纵向导轨长度l8、竖直连杆长度lCD=l6、竖直连杆长度lDE=l5。
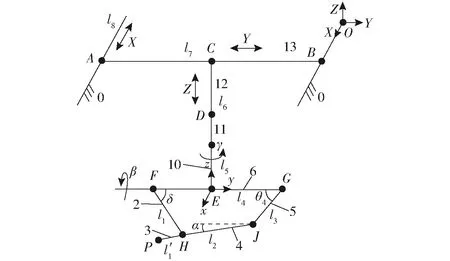
图3 6-DOF混联机构运动学建模
进一步,x、y、z方向的直线移动输入分别为S1、S2、S3,绕z轴转角为γ;平面四杆机构整体绕转动副R0轴线的转角为β,手抓3绕转动副R2轴线旋转的角度为α,输入转角为θ4,设手抓3与水平方向的辅助夹角为δ。
在右侧静导轨上建立静坐标系OXYZ,易知,A=(S1,-l7,0),B=(S1,0,0),C=(S1,-S2,0),D=(S1,-S2,-S3),E=(S1,-S2,-S3-l5)。
1.3 机构正解求解
已知:3个移动输入S1、S2、S3和3个转动输入角θ4、β、γ,求:手抓上点P的位置P=(x,y,z)及其姿态(α,β,γ)。
以平面四杆机构构件6之中点E为原点建立动坐标系oxyz,则在oxyz中,设四杆机构的初始位置在平面yoz上,各点坐标:E*=(0,0,0)、F*=(0,-l4/2,0)、G*=(0,l4/2,0)、J*=(0,l4/2-l3cosθ4,-l3sinθ4)、H*=(0,l4/2-l3cosθ4-l2cosα,-l3sinθ4-l2sinα)、P*=(0,l4/2-l3cosθ4-(l2+l′1)cosα,-l3sinθ4-(l2+l′1)sinα)。
其中,α、δ的计算可由几何约束关系lHJ=l2建立的位置方程整理,并简化得
A1sinα+B1cosα+C1=0
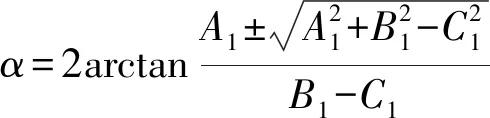
(1)
其中
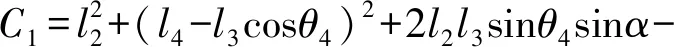
同时,也有
A2sinδ+B2cosδ+C2=0

(2)
其中A2=-2l1l3sinθ4B2=-2l1(l4-l3cosθ4)
在动坐标yoz平面上,四杆机构各坐标转换到静坐标系OXYZ的坐标为
(F,G,J,H,P)T=T×(F*,G*,J*,H*,P*)T+lOo′
其中
式中T——动坐标系相对于静坐标系的旋转矩阵[20]
lOo′——动平台原点o在静坐标系下的位置矢量
③疗效判定有效:自觉症状(疼痛、麻木、感觉异常)较前改善,体格检查(膝反射、跟腱反射)较前好转,但未达正常,神经传导速度较治疗前虽有所提升,但速度提升在5 m/s以下。显效:感觉无明显症状或症状有显著好转,膝反射及跟腱反射基本正常,神经传导速度接近或能够达到正常或加快速度≥5 m/s。无效:自觉症状无好转,膝反射及跟腱反射无好转,神经传导速度较治疗前无好转。显效+有效=总有效。
则各点坐标在静坐标系的坐标分别为
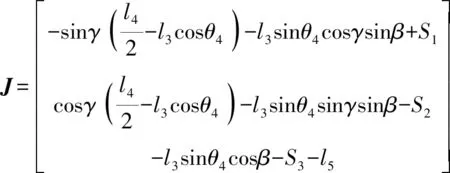
1.4 机构位置反解求解
已知:动平台上点P=(x,y,z,α,β,γ),求输入参数θ4、β、γ、S1、S2及S3。
(1)由α求θ4
由式(1)整理并简化得
A3sinθ4+B3cosθ4+C3=0
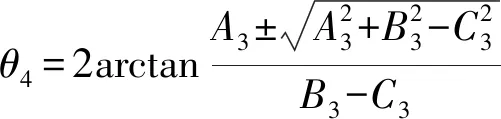
(3)
其中
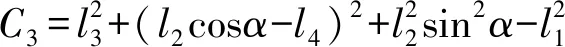
(2)β、γ为独立转动,显然β、γ易知。
(4)
1.5 正逆解验算
设该机构结构参数为:l1=200 mm,l2=250 mm,l3=150 mm,l4=400 mm,l′1=50 mm,β=30°,γ=50°。取输入位移S1、S2、S3分别为65、55、75 mm。
设输入角θ4=40°,由式(1)、(2)求得该机构的位置正解为α1=-59.970 5°,α2=22.599 6°。此时,点P坐标为(167.311 3,-34.254 8,16.432 6) mm与(143.940 7,-259.419 7,-308.341 8) mm。
进一步,将α1=-59.970 5°,α2=22.599 6°代式(3)、(4)得到该机构位置逆解如表1所示。

表1 位置逆解数值
表1中的第4组数值与正解一样,因此,正、逆解公式推导正确。
2 杆长优化
为了达到较高速采摘,同时减轻整个移动底盘正上方的悬挂质量,需要质量较轻的采摘机械手。因2-DOF的并联模块为一个需要整体绕水平Y轴大转动(β)的平面四杆机构,因此,其杆件材料采用高强度的工业铝7076,同时优化构件杆长。这样,在完全满足其运动要求和采摘效率的要求下,使其材料最少、杆件总长最短,成为较实用的选择方法。
2.1 设计变量
为简化优化过程,某些杆件长度由结构所需预先确定,剩余杆件长度由优化来确定,具体为:
(1)预先确定的参数主要为串联部分的尺寸参数,即:横向导轨长度lAB=l7=700 mm、纵向导轨长度l8=650 mm;竖直连杆长度lCD=l6=100 mm,竖直连杆2长度lDE=l5,可在长度0~50 mm范围内变化,其外部长度变化范围为0~150 mm。
(2)优化确定的参数主要为并联部分参数:设置lFG=l4=400、300、200、150 mm,lHP=l′1=50 mm,因此,只需优化3根杆长度,即l1、l2、l3。
因此,整个6-DOF机器人机构优化的设计变量为x=[x1x2x3]=[l1l2l3]。
2.2 目标函数
目标函数f(x)为机构总杆长(各杆件长度之和)最小,即minf(x)=l1+l2+l3。
2.3 约束条件
机构尺寸的具体要求为:①长×宽×高:650 mm×700 mm×500 mm。②移动量:X≤700 mm;Y≤650 mm;Z≤150 mm。③转角:α≤90°;0°≤β≤90°;0°≤γ≤360°。
(1)杆长约束条件(l3、l4分别为最短杆长、最长杆长)
g1(x)=l3-l2≤0
(5)
g2(x)=l3-l1≤0
(6)
g3(x)=l3-l4≤0
(7)
g4(x)=l2-l4≤0
(8)
g5(x)=l1-l4≤0
(9)
g6(x)=l3+l4-l1-l2≤0
(10)
(2)传动角约束条件(∠FHJ为传动角)
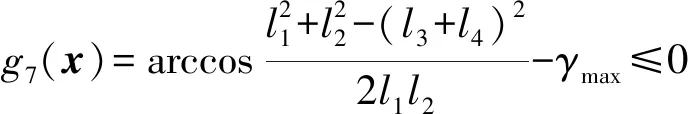
(11)
(12)
其中γmin=45°,γmax=135°。
2.4 优化结果
由上述优化模型(式(5)~(12)),运用非线性规划的fmincon求解最优方法,求得最长杆长l4=150 mm时的优化杆长,优化前后各杆参数如表2所示。
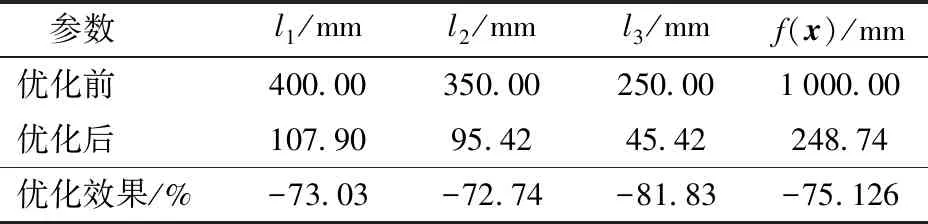
表2 优化前后杆长参数比较
由表2可知,机构参数优化后,3根杆的长度均有明显缩短,总长度比优化前减少751.26 mm,大大减少了采茶机器人的制造成本,并使采茶机构的尺度参数更加合理。同时,对其进行仿真分析,满足实际运动要求。
3 机构摆动力完全平衡分析
移动底盘平均速度为0.5 m/s,6-DOF 混联采摘机器人末端操作平均速度为1.0~1.5 m/s,可见其采摘速度较快。因整个机器人、特别是并联部分属于非对称布置,其高速运动情况下所产生的震动力较大,不仅会影响采摘机器人的性能和寿命,而且会影响采摘速度、精度和效率。因此,需要对整个悬挂的并联操作手进行动平衡分析和计算,移动行走机器人机架平均速度为0.5 m/s,6-DOF 混联采茶机构的末端操作手空载时平均速度为1.5 m/s,可见其保证了采摘效率,速度较快。因此,在速度运动较快的情况下,并联部分同时采用非对称布置,其高速运动下所产生的偏心力与偏心距较大,从而增加了采茶机械手的不稳定并引起振动,影响其采摘精度和机械使用寿命。因此,需要对整个悬挂的并联操作手进行动平衡分析,完全平衡是给杆件添加其他位置和远超杆件本身质量,使得整个机构的质心位置在运动时保持恒定,从而使摆动力为0。
3.1 有限位置法
有限位置法[21-22]是对树枝构件添加配重以实现摆动力完全平衡,平衡时,机构在任意位置上的总质量矩为同一常量。因此,可取若干个位置上的质量矩建立线性方程组,即为摆动力完全平衡条件。
3.2 机构添加配重位置建模
图4为6-DOF混联采茶机构的摆动力平衡配重设计方案,其中,pi、qi(i=1,2,3,4)为各杆件重心位置参数。
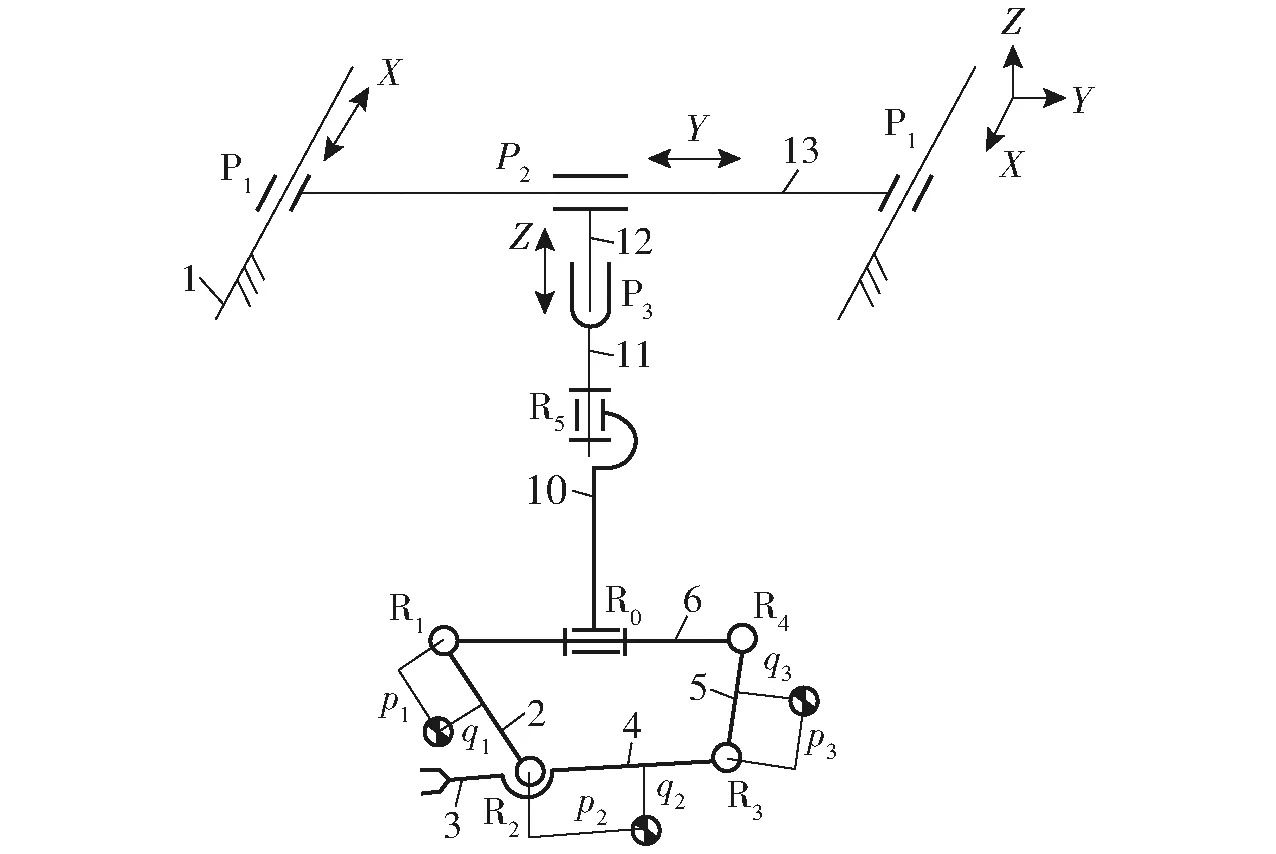
图4 机构配重方案
3.3 机构未平衡时总质量矩
该机构由并联部分的平面四杆机构和串联部分组成,对本机构而言,主要由并联部分产生摆动力,故对该部分进行平衡分析。
设mi、ri(i=1,2,3,4)分别表示构件i质量、质心位置。
构件1、2、3、4质心位置分别为
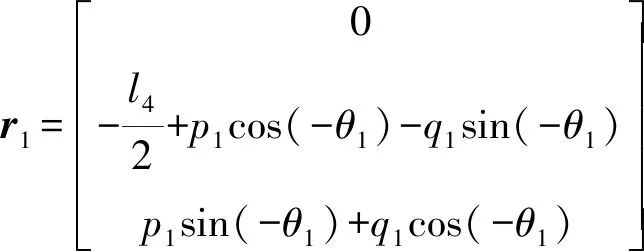
因此,并联部分平面四杆机构总质量矩为
MR=m1r1+m2r2+m3r3+m4r4
式中M——构件1、2、3、4总质量
R——平面四杆机构总质心位置
则有
在不同位置θik时,机构总质量矩可写为
(13)
式中θik、αik——在不同机构运动位置时构件位置角
i——构件编号
k——机构运动位置编号
3.4 摆动力完全平衡条件及其配重参数求解
3.4.1机构平衡后总质量矩
对树枝构件1、2、3进行配重,连枝构件4不添加配重。因此,机构添加配重后总质量矩为
(14)



3.4.2机构摆动力完全平衡条件
机构总质量矩为零时,机构摆动力完全平衡,即
基于有限位置法进行摆动力完全平衡时,有限的任一位置质量矩恒为一个常数。则有
式中 [MRx]j、[MRy]j、[MRz]j——机构在j位置时在x、y、z方向上的质量矩分量
[MRx]0、[MRy]0、[MRz]0——机构初始位置时在x、y、z方向上的质量矩分量
即
(15)
其中 ΔCij=cosθij-cosθi0ΔSij=sinθij-sinθi0
式中fi——各构件配重参数系数
3.5 机构摆动力完全平衡数值求解
由第2节优化后杆长参数可知:l1=107.9 mm,l2=95.42 mm,l3=45.42 mm,l4=150 mm,l′1=50 mm。
各杆件的质量参数:m1=0.125 34 kg,m2=0.109 66 kg,m3=0.046 82 kg,m4=1.782 42 kg,m′1=0.062 63 kg。
各构件的质心位置参数为:设每个杆件均为均质杆,其质心为杆件的几何中心,即pi=li/2(i=1,2,3,4),qi=0(i=1,2,3,4),具体为:p1=53.95 mm,p2=47.71 mm,p3=22.71 mm,p4=75 mm,p′1=25 mm。
由式(14)可知,共有6个未知数,每个位置可有2个位置方程。因此,需要3组位置方程才能求解,即需要4个位置。在4个位置上分别取驱动角θ4为0°、20°、40°、60°,计算得到完全相同的构件配重参数,为
ΔC1j=(ΔC11,ΔC12,ΔC13)=
(-0.121 0,-0.098 4,-0.066 9)
ΔS1j=(ΔS11,ΔS12,ΔS13)=
(0.106 2,0.118 6,0.108 7)
ΔC2j=(ΔC21,ΔC22,ΔC23)=
(0.148 4,0.137 1,0.101 8)
ΔS2j=(ΔS21,ΔS22,ΔS23)=
(-0.085 0,-0.114 3,-0.118 9)
ΔC3j=(ΔC31,ΔC32,ΔC33)=
(-0.060 3,-0.173 6,-0.266 0)
ΔS3j=(ΔS31,ΔS32,ΔS33)=
(0.342 0,0.300 8,0.223 2)
将各杆件杆长、质量、质心位置参数及ΔCij、ΔSij,代入式(14)中,此时,取不同组输入角位置时,求解得到构件1、2、3的配重参数为
(16)
(17)
(18)
3.6 摆动力完全平衡效果验证
采用机构质心位置和摆动力总量及其分量都保持恒定的方法,验证摆动力完全平衡的正确性。
机构总质心为
(19)
机构总摆动力为
(20)
其中
式中mμ——各构件质量μ——构件编号
n——活动构件数
3.6.1摆动力平衡前后质心轨迹对比
将所设置的配重质心位置和质量参数代入式(19),并用Matlab绘制摆动力完全平衡前后机构总质心轨迹及其在x、y、z方向上的轨迹,如图5所示。由图5a可知,平衡前,机构总质心的波动面域较大;平衡后,机构总质心在点(0,21.6,0)mm处保持静止。由图5b可知,平衡前后,质心在x方向的轨迹保持不变,即质心在yoz平面上运动。由图5c、5d可知,平衡前,机构总质心在y、z轴方向的质心轨迹波动极差(曲线中最大值与最小值之差)分别为24.2、24.1 mm;平衡后,机构总质心轨迹在y、z方向上都保持静止。
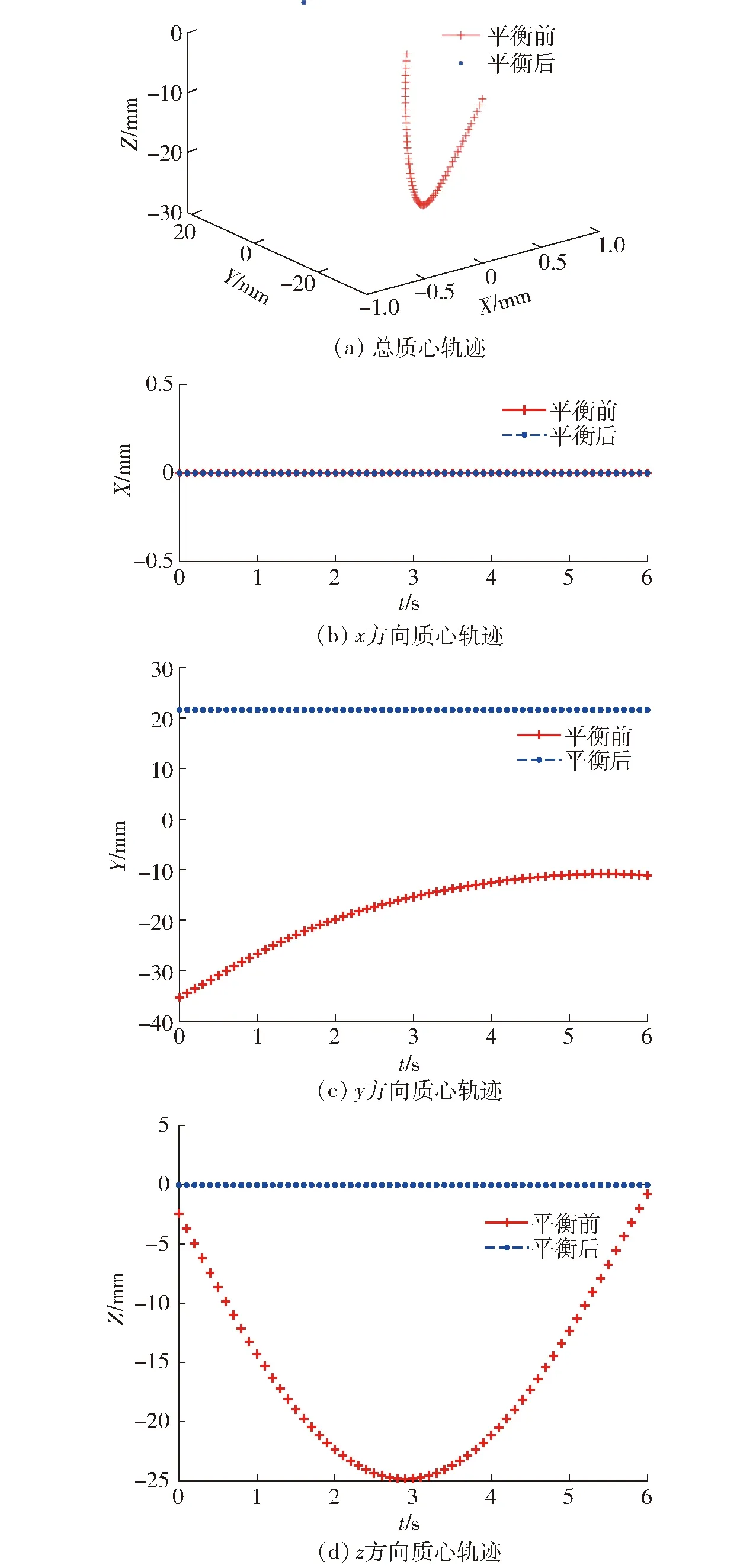
图5 摆动力完全平衡前后机构总质心轨迹对比
3.6.2摆动力平衡前后机构总摆动力
将所设置的配重质心位置和质量参数代入式(20),并用Matlab绘制出摆动力完全平衡前后机构的总摆动力及其在x、y、z方向上的摆动分力,如图6所示。
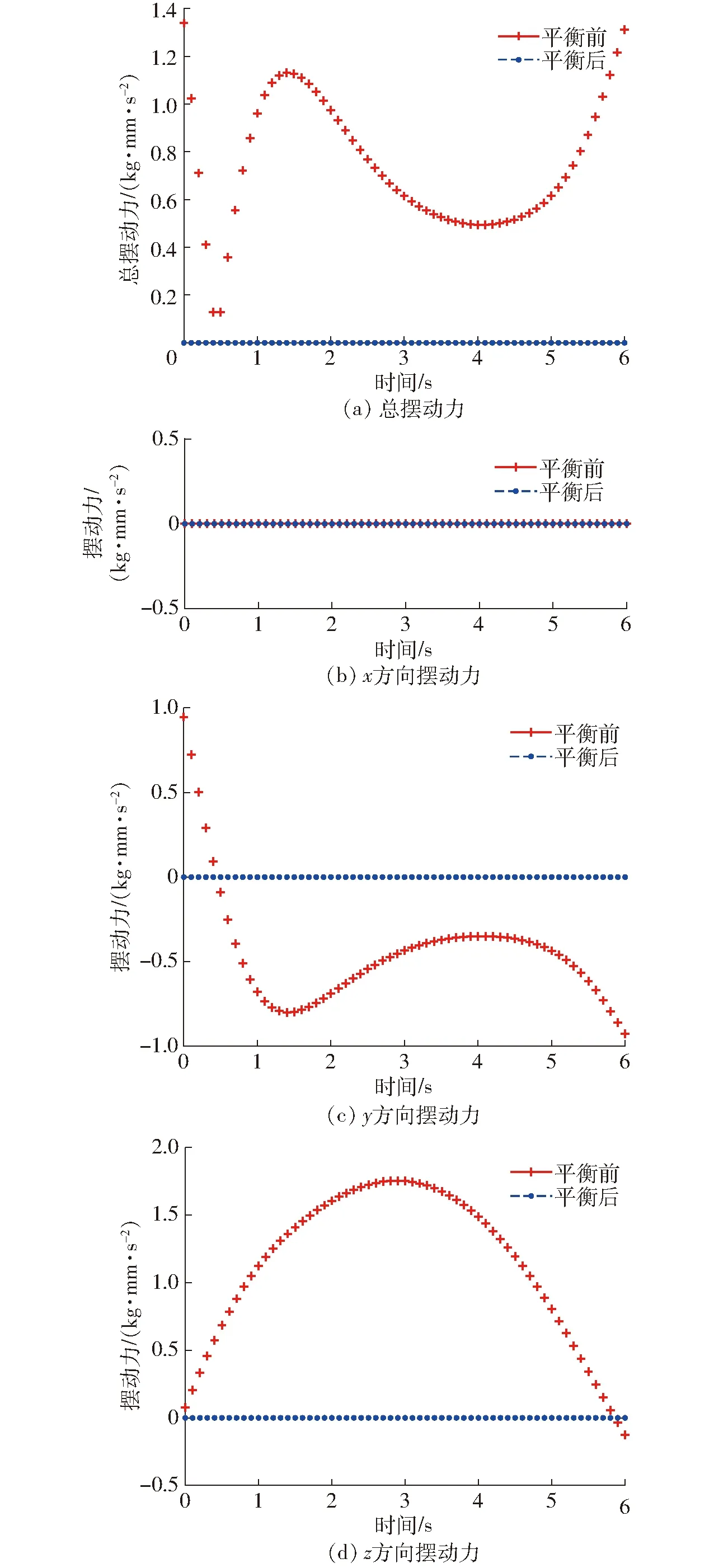
图6 摆动力完全平衡前后机构摆动力对比
由图6可知,平衡前,机构摆动力在x、y、z方向的极差分别为0、1.88、1.88 kg·mm/s2,总摆动力极差为1.2 kg·mm/s2。平衡后,机构对机架的作用力为零。
综上可知:平衡后机构总质心位置不变,且对机架的作用力为零。因此,摆动力完全平衡的有限位置法有效。
完全平衡可使得整个机构的质心位置在运动过程中保持恒定,从而使摆动力为零,但添加的质量超过杆件本身的质量;在实际应用时,一般采取在合适的位置上布置较小的质量,使得整个机构所产生的摆动力最小,因此,常采用对整个机构进行摆动力部分平衡设计与优化。
4 机构摆动力部分平衡优化设计
从基于有限位置法的机构摆动力完全平衡后的效果可以看出,机构所配重的质心位置参数已远超机构杆长,使机构额外质量增大。因此,从实际应用的角度出发,仅对摆动力进行部分平衡优化即可,即所增加的配重质心位置和质量参数都设置在可接受的范围之内,达到部分平衡。
遗传算法(GA)相较于其他的优化算法,具有目标群体大、优化计算更加精确的优点。因此,应用遗传算法对该机构进行摆动力部分平衡优化。
4.1 优化模型
4.1.1机构目标函数确定
目标函数取为总机构摆动力均方根最小,即
(21)
其中
式中Fx、Fy、Fz——摆动力在x、y、z方向上的分量
4.1.2设计变量和约束条件确定
将配重质量设置为杆质量的0.2~5倍,配重位置为杆长的0~1倍,如表3所示。
4.2 优化过程
4.2.1算法基本参数及优化结果
遗传算法基本参数为:种群规模20、最大迭代次数147、交叉概率0~1、变异概率0~1、摆动权重0.4、加速系数2、缩放因子0~1、交叉因子 0.8~1。
将设置的配重质心位置和质量代入式(21),利用Matlab算法工具箱,计算出优化结果如表4所示。

表4 部分平衡优化结果
4.2.2摆动力部分平衡后与平衡前对比
(1)总质心轨迹
由图7a可知,机构部分平衡前后,机构总质心轨迹区域大大减少,其在x、y、z的质心轨迹如图7b~7d所示。

图7 摆动力部分平衡前后质心轨迹对比
由表5可知,摆动力部分平衡后,机构总质心轨迹在y、z方向上的波动分别减少53.72%、25.10%,其中,机构在y轴方向上的质心轨迹波动优化效果最优。

表5 质心轨迹在各方向上优化效果
(2)摆动力部分平衡前后机构摆动力
如图8a所示,在x、y、z方向上的摆动力即Fx、

图8 摆动力部分平衡前后总摆动力对比
Fy、Fz,x、y、z的部分摆动力如图8b~8d和表6所示。

表6 摆动力在各方向上的优化效果
由图8和表6可知,摆动力部分平衡优化后,虽然在z方向上的优化效果一般,但总摆动力整体优化效果比较明显,证明了摆动力部分平衡优化的有效性。
5 结论
(1)提出了一种安装于移动底盘的6-DOF混联采茶机器人机构,机构具有较好的新颖性;并对机构进行了位置正逆解计算及验证。
(2)运用非线性规划法,以机构总杆长最短为优化目标对机构杆长进行优化,优化效果较为显著。
(3)采用有限位置法对该机构的摆动力进行完全平衡设计和分析;又运用遗传算法对机构进行摆动力部分平衡优化设计,优化后质心轨迹在y、z方向上的波动分别减小53.72%、25.10%,而摆动力在y、z方向上的波动分别减小52.66%、-17.02%,总摆动力减小43.33%,达到部分平衡优化的目的。

