基于群智能优化算法的土壤水动力参数反演

苏李君 郭 媛 陶汪海 张亚玲 单鱼洋 王全九,

(1.西安理工大学理学院, 西安 710054; 2.西安理工大学西北旱区生态水利国家重点实验室, 西安 710048;3.西安理工大学水利水电学院, 西安 710048)

0 引言

在土壤物理学中,一般采用Richards方程描述非饱和土壤水分运动[1],而描述土壤含水率与基质势关系的土壤水分特征曲线模型是求解Richards方程的关键。常用的土壤水分特征曲线模型有Gardner模型[2-3]、Brooks-Corey模型[4]、Gardner-Russo模型[5]、Van Genuchten模型[6]等。由于这些模型的高度非线性,导致通过田间或室内直接测定土壤水动力性质费时费力,且易引入较大的不确定性,因此间接估计土壤水动力参数的方法越来越受到重视。目前,许多学者基于遗传算法和粒子群算法提出了土壤水分特征曲线模型参数的反演方法[7-16]。杨坤等[7]基于遗传算法建立了土壤水分运动参数识别的优化计算模型,并通过土壤含水率实测值验证了模型的可行性。由于遗传算法全局搜索能力极强,但局部寻优能力较差,郭向红等[8]通过Levenberg-Marquardt算法较强的局部优化能力来提高遗传算法的收敛速度,提出了反演土壤水动力参数的混合遗传算法。陈大春等[10]、马亮[11]分别采用随机粒子群算法和改进粒子群算法构建了Van Genuchten模型参数的反演模型。

群智能优化算法是一种具有全局优化性能、通用性强且适合于并行处理的算法,在解决大空间、非线性、全局寻优、组合优化等复杂问题方面具有独特的优势[17]。莫愿斌等[18]提出一种改进萤火虫算法(GSOPB)对Van Genuchten模型参数进行优化。为了解决土壤水分特征曲线 Van Genuchten 模型参数优化的非线性拟合问题,付强等[19]提出了可变步长的改进萤火虫算法(MFA),与粒子群算法、遗传算法、萤火虫算法相比,该算法模拟结果精度更高,适用性更强。与萤火虫算法相比较,鲸鱼优化算法和灰狼优化算法具有收敛速度快、寻优精度高和全局寻优能力强等优点[20-21]。本文基于数值模拟和代数方程,采用鲸鱼优化算法和灰狼优化算法对土壤水动力参数进行反演,旨在为土壤水动力参数的反演提供新的途径和方法。

1 材料与方法

1.1 土壤水分运动方程

一维非饱和土壤条件下的达西定律可表示为

(1)

式中q——土壤水分通量,cm/min

K(h)——非饱和土壤导水率,cm/min

h——土壤水吸力,cm

z——空间坐标值,向上为正,cm

φ——流动方向与垂直轴之间的夹角(即垂直流动φ=0°,水平流动φ=90°)

假设土壤为均质、各向同性的刚性多孔介质,则在初始含水率分布均匀的条件下,一维垂直入渗问题可用Richards方程表示为

(2)

式中θ——土壤体积含水率,cm3/cm3

T——时间,min

θ0——初始含水率,cm3/cm3

θs——土壤饱和含水率,cm3/cm3

为求解方程,BROOKS-COREY提出了一个描述土壤含水率和土壤基质势之间关系的模型

(3)

式中Se——有效饱和度

θr——土壤滞留含水率,cm3/cm3

n——形状系数

hd——进气吸力,cm

根据Mualem模型[22],式(1)中的非饱和导水率K(h)可以表示为

(4)

式中Ks——饱和导水率,cm/min

m——参数

基于HYDRUS-1D[23-25]软件模拟的数据,本文采用智能优化算法反演土壤水动力参数,反演的参数主要有θr、θs、hd、n和Ks。通过反演得到的参数计算相应的累积入渗量、入渗率、湿润锋深度和含水率数据,并进行误差分析。采用相对误差Re[26]和决定系数R2[26]来验证群智能优化算法反演参数的准确度。

1.2 数据来源

HYDRUS-1D[23-25]软件可以用来模拟不同初始和边界条件下的一维土壤水分运动。因此,本文使用HYDRUS-1D模拟非饱和土壤水分在初始含水率均匀分布、定水头条件下的一维垂直非饱和土壤水分入渗过程,并生成不同时间的累积入渗量、入渗率、湿润锋深度和土壤含水率数据。将模拟时间10等分,基于生成的数据构建目标函数,采用智能优化算法对土壤的水动力参数进行反演。表1列出了美国农业部分类方案中11(土壤序号1～11)个土壤结构[26]的土壤水动力参数。土壤12的土壤水动力参数、累积入渗量、入渗率、含水率、湿润锋深度、入渗时间等数据来自马东豪等[27]的实测试验数据,用于验证本文方法的可行性。

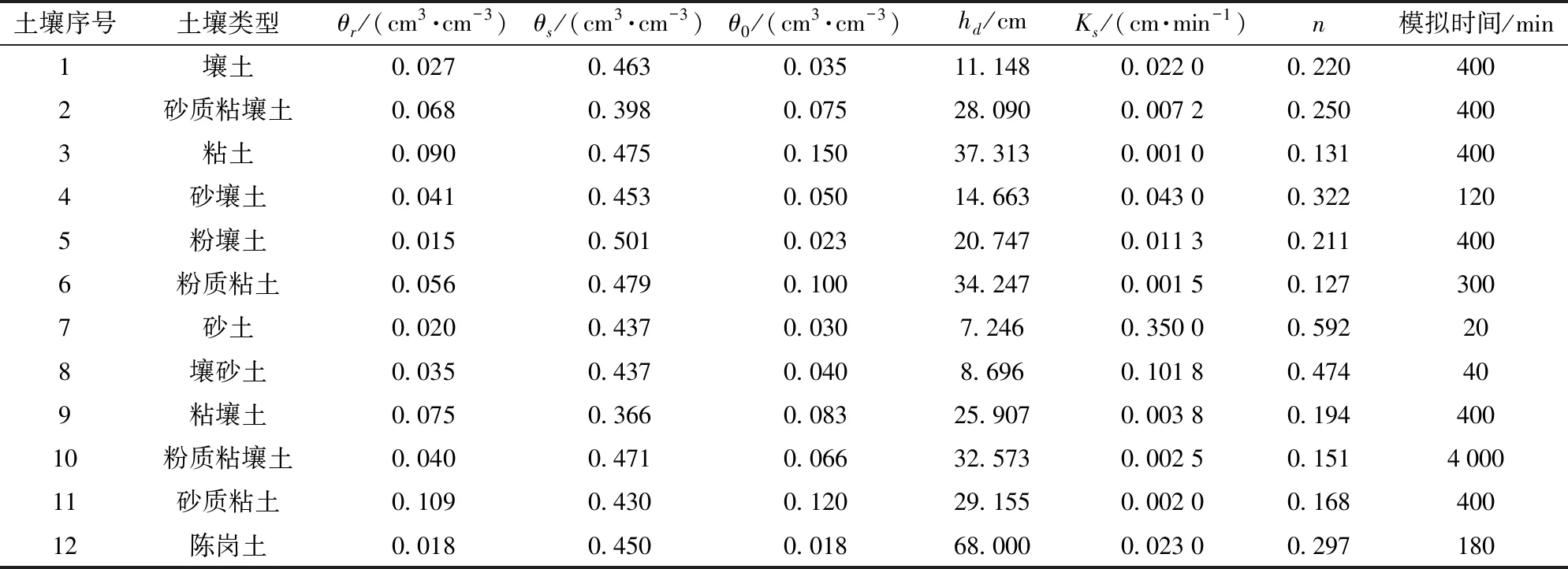
表1 土壤水动力参数

1.3 代数方法

代数方法是利用非饱和土壤水分垂直入渗问题的解析解[27-29]构建反演模型的目标函数。首先将群智能优化算法随机生成的土壤水动力参数代入解析解,获得累积入渗量I、入渗率i、土壤含水率θ和入渗时间T的代数解,再与HYDRUS-1D模拟得到的结果作比较,最后优化出使得目标函数最小的一组参数。选取SU等[28]提出的解析解构建模型,代数表达式为

(5)

(6)

(7)

(8)

其中

式中zf——湿润锋深度

其中,T根据三点高斯求积公式计算得到。

1.4 数值方法

数值方法是利用有限差分法构建土壤水分运动方程的数值模拟模型,并将群智能优化算法随机生成的土壤水动力参数代入数值模型,模拟得到累积入渗量I、入渗率i和土壤含水率θ的数值解数据,再与HYDRUS-1D模拟得到的结果作比较,优化出使目标函数最小的一组参数。具体的有限差分格式为:

式中 Δx——空间步长,cm

Δt——时间步长,min

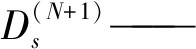
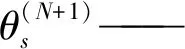
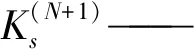
为了验证差分格式与HYDRUS-1D模拟结果的一致性,将表1中壤土参数代入差分格式中,得到的累积入渗量、入渗率和含水率与HYDRUS-1D模拟结果相比较,相对误差分别为1.13%、1.59%、3.16%,决定系数分别为0.999 3、0.991 2、0.986 4,由此可见两种数值方法的模拟结果具有一致性。因此,本文采用差分格式与群智能算法相结合构建数值反演方法。

1.5 目标函数

选取合适的目标函数能有效解决参数反演的非唯一性问题,提高反演结果的精确度[30],所以目标函数的选取极其重要。本文采用累积入渗量、时间、含水率、湿润锋深度的误差构建目标函数。在代数方法中,选取模拟时间10等分所对应的累积入渗量、湿润锋深度以及最终时刻10个深度上的土壤含水率,并将湿润锋深度代入式(8)计算相应的入渗时间,根据入渗时间、累积入渗量和土壤含水率构建目标函数,因此代数方法可采用目标函数1和目标函数2进行反演。

目标函数1

(9)

式中o——目标函数值

I1i——累积入渗量的近似解

Ii——HYDRUS-1D模拟得到的累积入渗量

Tci——入渗时间的近似解

Ti——HYDRUS-1D模拟得到的入渗时间

目标函数2

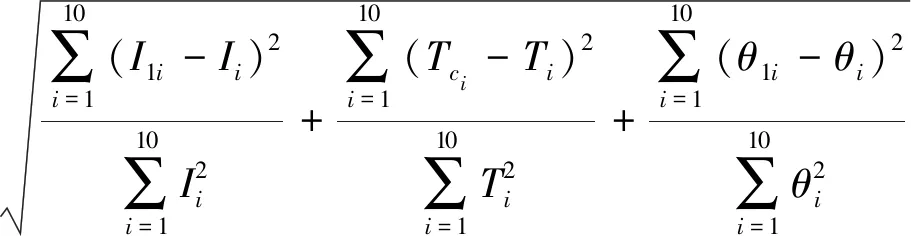
(10)

式中θ1i——土壤含水率的近似解

θi——HYDRUS-1D模拟得到的土壤含水率

在数值方法中,选取与HYDRUS-1D模拟中相同时间下的累积入渗量、湿润锋深度以及相同深度的土壤含水率建立目标函数,因此数值方法采用目标函数3进行反演。

目标函数3

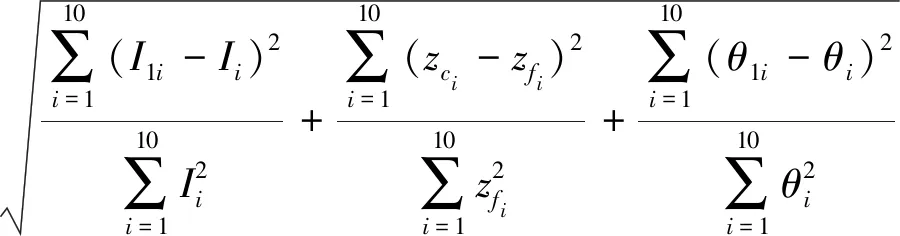
(11)

式中zci——差分格式模拟得到的湿润锋深度

1.6 群智能优化算法

1.6.1鲸鱼优化算法

鲸鱼优化算法(Whale optimization algorithm,WOA)[31]是模仿座头鲸的觅食行为提出的一种新型启发式优化算法。该算法主要包含包围、捕食和搜索猎物3个阶段。

包围阶段数学模型为

X(t+1)=X*(t)-(2ar-a)|CX*(t)-X(t)|

(12)

式中t——当前迭代次数

X*(t)——第t代全局最优位置

X(t)——第t代个体位置

a——常数,从2线性减少到0

r——[0,1]中的随机向量

C——[0,2]中的随机向量

每个鲸鱼个体在朝目标游动时,采取缩小包围圈和螺旋前进两种策略,为使这两种方式同时进行,在建模中设置执行优化任务时选择两种行进方式的概率均为50%,捕食阶段数学模型表示为

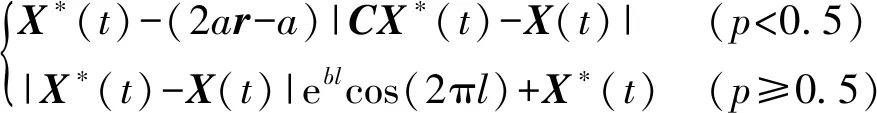
(13)

式中b——常数l——[0,1]中的随机数

p——[0,1]中的随机数

搜索猎物阶段数学模型为

X(t+1)=Xrand-(2ar-a)|CXrand-X(t)|

(14)

式中Xrand——从当前种群中选择的随机位置(随机鲸鱼)

综上所述,鲸鱼优化算法的流程图如图1所示,A为协同系数向量。

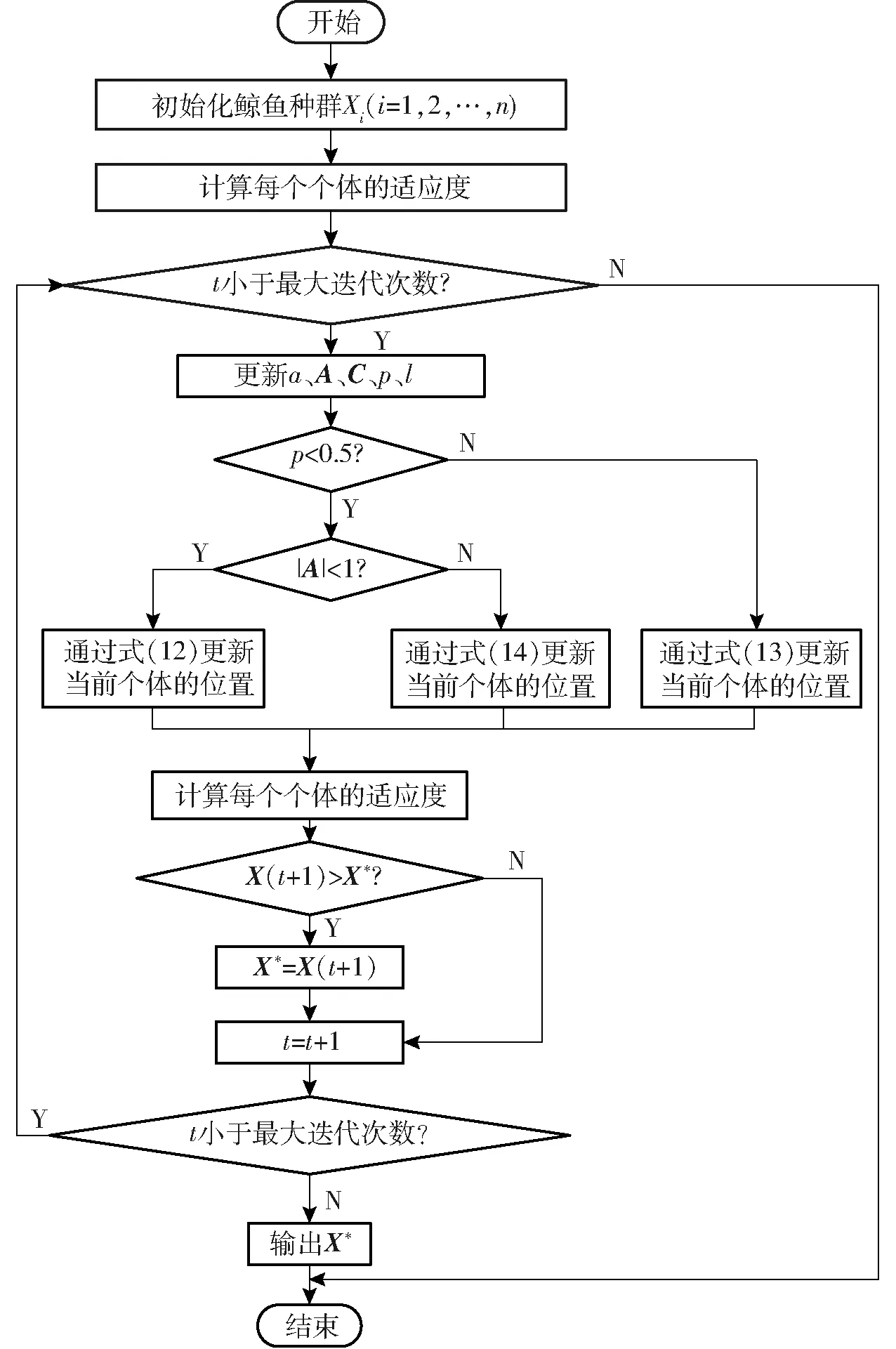
图1 鲸鱼优化算法流程图

1.6.2灰狼优化算法

灰狼优化算法(Grey wolf optimizer,GWO)是由MIRJALILI等[32]提出的一种群智能优化算法。将狼群中适应度最好的3匹灰狼依次标记为α、β、δ,而剩下的灰狼标记为ω。灰狼捜索猎物时会逐渐地接近猎物并包围它,该行为数学模型为

X(t+1)=Xp-|2ar3-a||2r4Xp-X(t)|

(15)

式中Xp——猎物位置

r3、r4——[0,1]中的随机向量

在每次迭代过程中,保留当前种群中的最好3只灰狼(α、β、δ),然后根据它们的位置信息来更新其它搜索代理(包括ω)的位置。该行为数学模型为

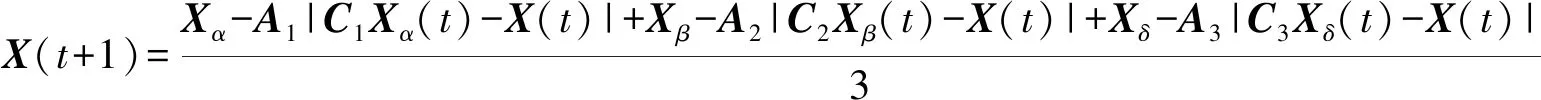
(16)

式中Xα、Xβ、Xδ——当前种群中α、β、δ的位置向量

A1、A2、A3——协同系数向量

C1、C2、C3——协同系数向量

综上所述,灰狼优化算法的流程图如图2所示。

图2 灰狼优化算法流程图

1.7 优化过程

利用群智能优化算法求解土壤水动力参数的基本思想是:根据土壤水分特征曲线模型确定待优化参数,即决策变量,种群中每个个体所处空间位置均包含一组决策变量。分别选择目标函数1、2、3作为适应度函数,通过适应度函数来衡量个体所处空间位置的优劣,利用搜索策略不断更新种群个体位置直至获取最佳空间位置,即获得待优化问题的最佳决策变量。本文针对代数与数值两种方法构建的目标函数,采用鲸鱼优化算法和灰狼优化算法反演Brooks-Corey-Mualem模型参数,利用Matlab软件分别对代数和数值的群智能优化算法进行程序编写,算法流程如图3所示。

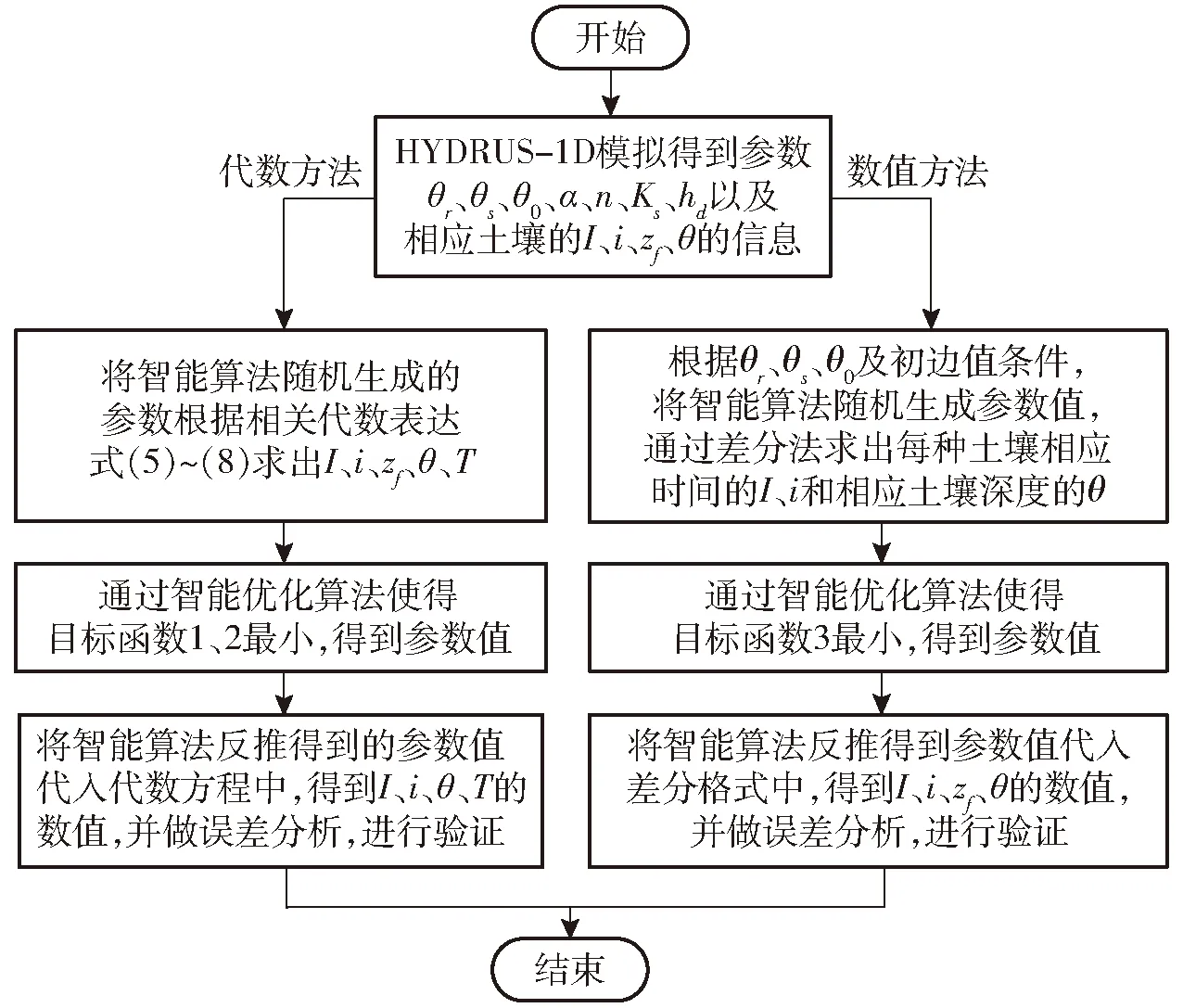
图3 代数方法与数值方法反演Brooks-Corey-Mualem参数优化过程

2 结果与分析

2.1 代数方法反演结果

基于代数方法,采用鲸鱼优化算法和灰狼优化算法对11种土壤的θr、θs、hd、n、Ks共5个参数进行反演,或者固定几个参数值时反演其他参数值。在优化算法中,设置种群个数为500,最大迭代次数为3 000,平均运行时间为70 s。以壤土为例,参数反演结果如表2所示。11种土壤参数的反演结果表明,鲸鱼优化算法在目标函数1和目标函数2下目标函数值的范围分别为0.004 31～0.060 32和0.030 74～0.084 76,参数反演值的相对误差平均值为0.24%～27.76%和0.38%～23.82%;灰狼优化算法在目标函数1和目标函数2下目标函数值的范围分别为0.004 14～0.060 32和0.013 08～0.073 31,参数反演值的相对误差平均值为0.12%～27.71%和0.23%～25.14%。对于两种群智能优化算法,虽然目标函数1的目标函数值小于目标函数2,但目标函数1的参数误差大于目标函数2。因此,为了更准确地反演参数,可选取目标函数2为适应度函数。

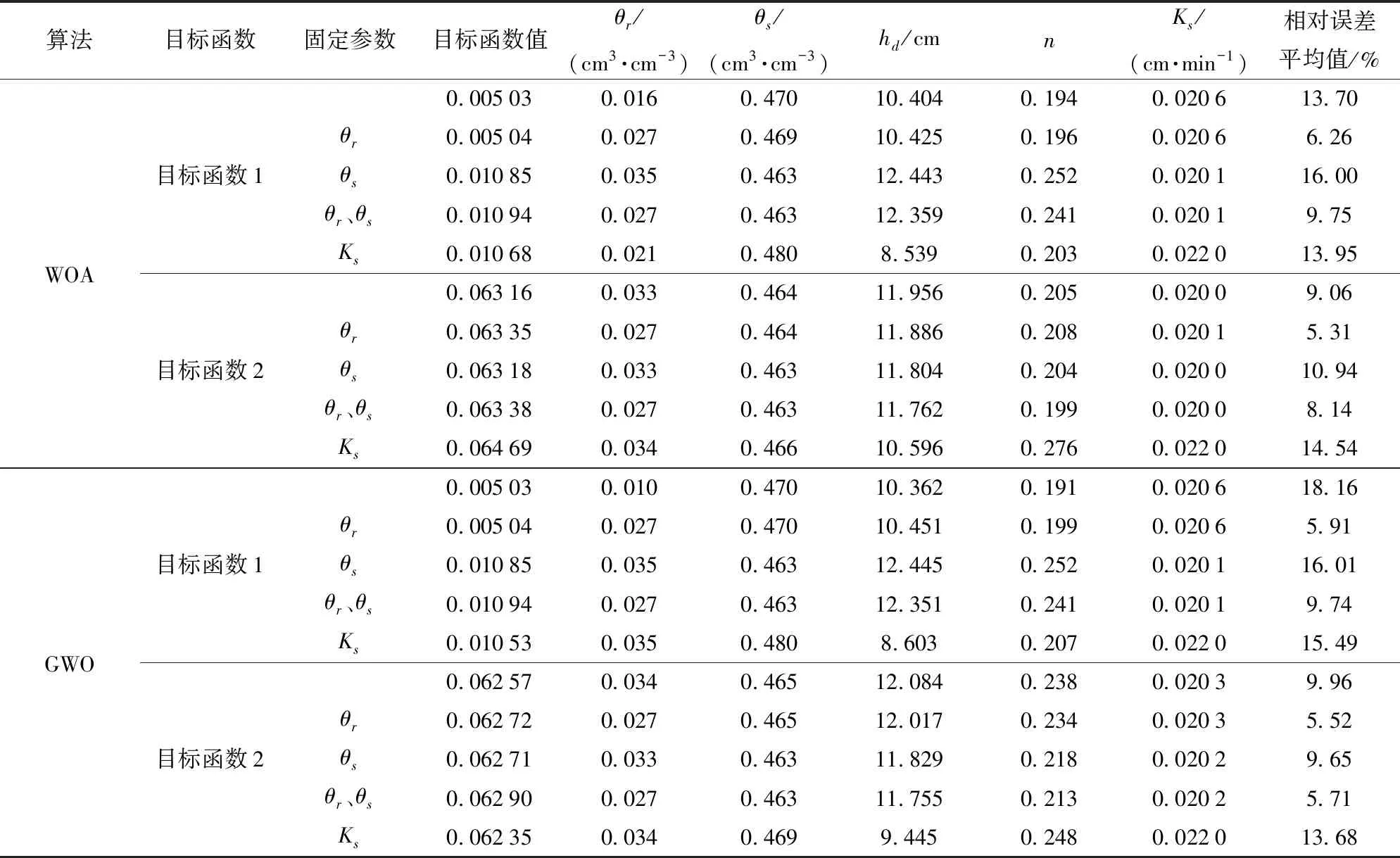
表2 不同优化算法及目标函数下壤土参数反演结果

针对11种土壤的参数,在目标函数2下,鲸鱼优化算法反演θr、θs、hd、n、Ks的相对误差分别不超过47.02%、0.06%、4.97%、17.01%和3.18%,灰狼优化算法反演θr、θs、hd、n、Ks的相对误差分别不超过53.43%、0.12%、7.31%、17.06%和3.62%。从参数误差可以看出,θr的反演误差较大。

由于θr、θs和Ks可以通过室内试验测量得到[33],因此可考虑固定这3个参数,反演其他参数值。当固定θr时,鲸鱼优化算法反演θs、hd、n、Ks的相对误差不超过0.05%、6.43%、14.20%、2.34%,灰狼优化算法反演的相对误差不超过0.13%、8.92%、25.80%、3.38%;当固定θs时,鲸鱼优化算法反演θr、hd、n、Ks的相对误差不超过43.67%、8.72%、15.10%、2.45%,灰狼优化算法反演的相对误差不超过45.79%、8.78%、15.17%、4.44%;当固定Ks时,鲸鱼优化算法反演θr、θs、hd、n的相对误差不超过47.36%、0.12%、9.00%、12.90%,灰狼优化算法反演的相对误差不超过47.27%、0.12%、5.26%、13.87%;当同时固定θr和θs时,鲸鱼优化算法反演hd、n、Ks的相对误差不超过3.97%、10.92%、2.67%,灰狼优化算法反演的相对误差不超过10.02%、17.98%、3.78%。

在目标函数2下,对于11种土壤反演得到的参数,不固定参数时鲸鱼优化算法反演θs、hd、n、Ks4个参数的相对误差平均值为0.01%～4.45%,固定θr反演θs、hd、n、Ks4个参数的相对误差平均值为0.11%～6.93%,固定θs反演hd、n、Ks3个参数的相对误差平均值为0.22%～5.23%,固定Ks反演θs、hd、n3个参数的相对误差平均值为0.02%～4.38%,固定θr、θs反演hd、n、Ks3个参数的相对误差平均值为0.23%～3.81%;不固定参数时灰狼优化算法反演θs、hd、n、Ks4个参数的相对误差平均值为0.05%～4.89%,固定θr反演θs、hd、n、Ks4个参数的相对误差平均值为0.39%～6.89%,固定θs反演hd、n、Ks3个参数的相对误差平均值为0.35%～5.26%,固定Ks反演θs、hd、n3个参数的相对误差平均值为0.03%～4.67%,固定θr、θs反演hd、n、Ks3个参数的相对误差平均值为0.37%～6.34%。

综上可知,在目标函数2下,不固定参数时选用鲸鱼优化算法反演θs、hd、n、Ks4个参数的精度优于灰狼优化算法;固定参数θr时灰狼优化算法反演θs、hd、n、Ks4个参数的精度优于鲸鱼优化算法;固定参数θs时鲸鱼优化算法反演hd、n、Ks3个参数的精度优于灰狼优化算法;固定参数Ks时鲸鱼优化算法反演精度优于灰狼优化算法;固定参数θr和θs时,鲸鱼优化算法反演hd、n、Ks3个参数的相对误差最小,反演效果最好,反演结果如表3所示。

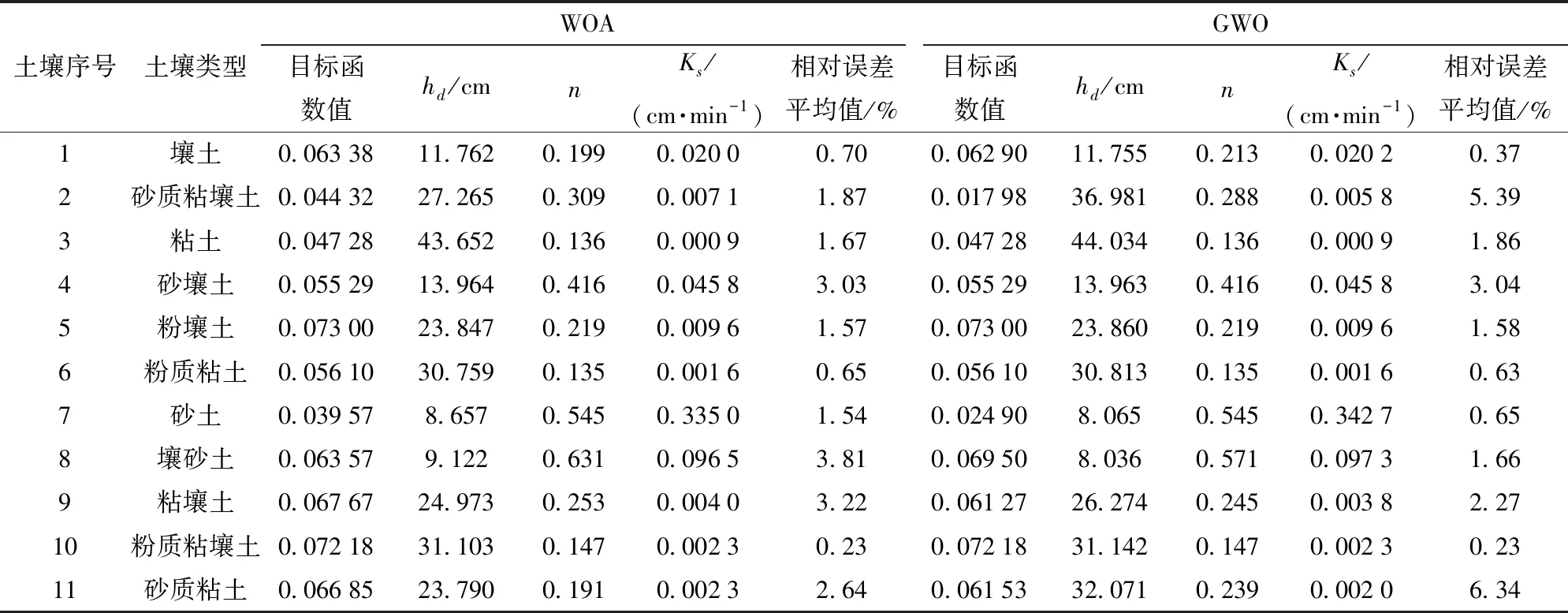
表3 目标函数2下鲸鱼优化算法和灰狼优化算法固定θr、θs反演其他参数值结果

以壤土、砂质粘壤土、粘土、砂壤土为例,将鲸鱼优化算法在目标函数2固定参数θr、θs下反演得到的参数代入式(5)～(7)中,得到的累积入渗量、入渗率、土壤剖面含水率的代数解与HYDURS-1D的结果作比较,比较结果如图4～6(其中,代数解是在固定参数θr、θs下鲸鱼优化算法针对目标函数2反演得到)所示。从图4～6可知,代数解与HYDURS-1D模拟得到的结果基本一致,11种土壤的累积入渗量、入渗率、含水率的相对误差都在9.74%以下,决定系数都在0.904 0以上。这表明,鲸鱼优化算法在目标函数2固定参数θr、θs下反演得到的土壤参数可以较为准确地描述土壤水分运动。

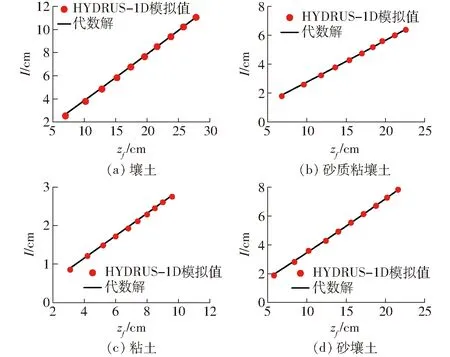
图4 代数方法与HYDRUS-1D模拟得到的累积入渗量对比

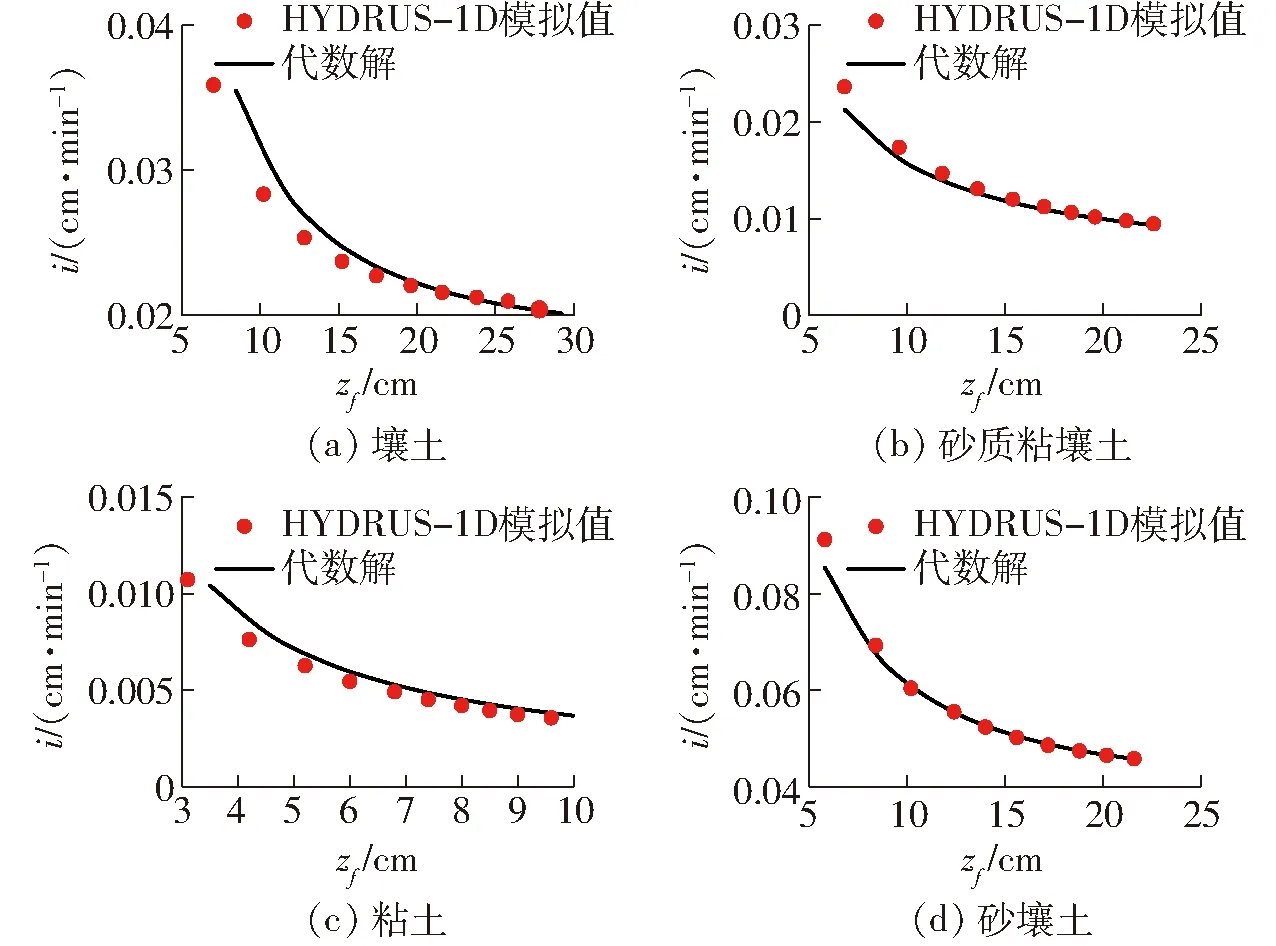
图5 代数方法与HYDRUS-1D模拟得到的入渗率对比

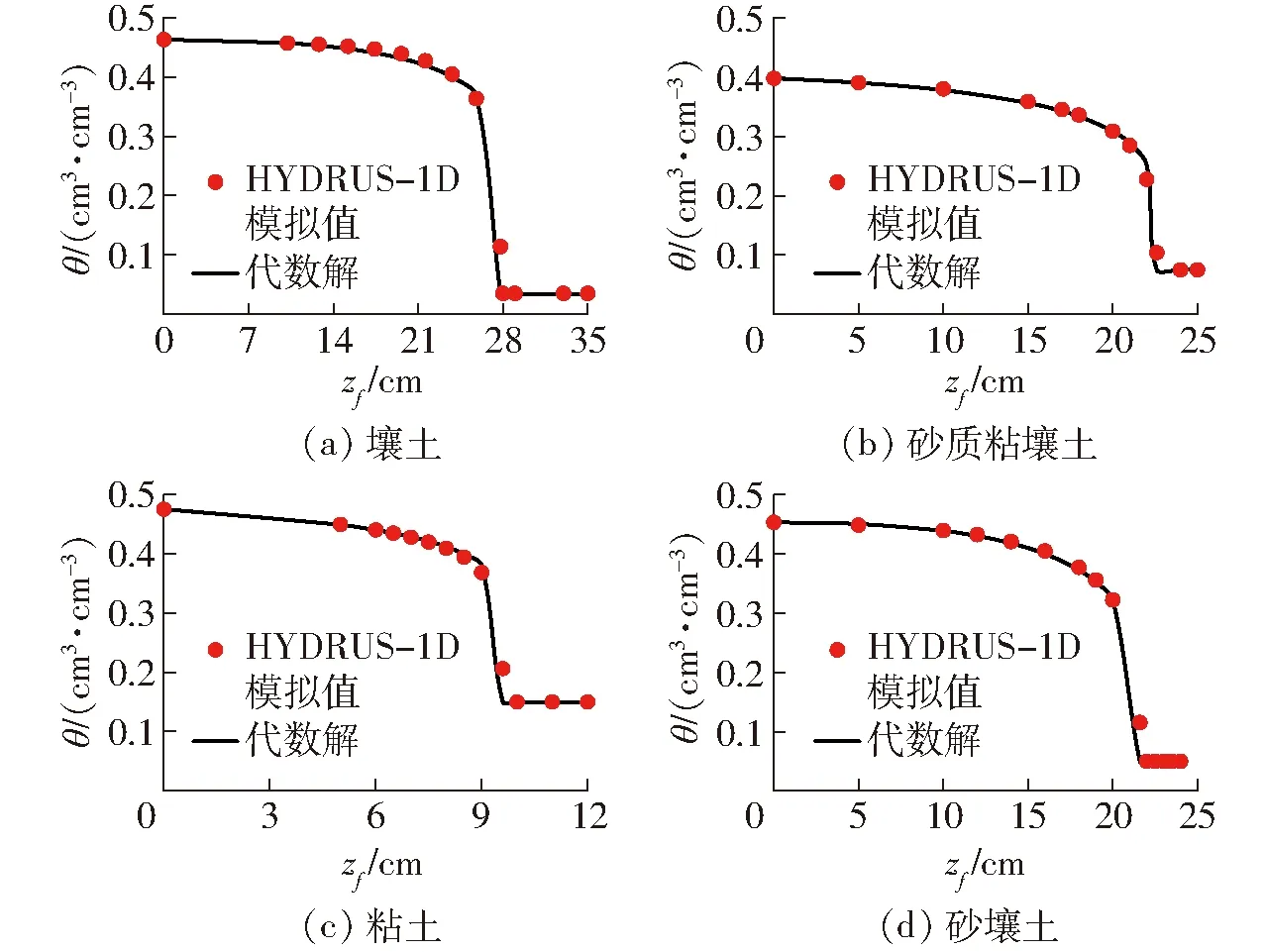
图6 代数方法与HYDRUS-1D模拟得到的土壤剖面含水率对比

2.2 数值方法反演结果

相对于代数方法,数值方法计算量较大,因此在优化算法中,设置种群个数为50,最大迭代次数为100,平均运行时间为115 s。11种土壤参数的反演结果表明:在鲸鱼优化算法下,除了砂壤土和粉质粘壤土的目标函数值分别为0.170 25和0.093 26外,其余土壤的目标函数值均在0.000 22～0.008 70之间,11种土壤反演结果的相对误差平均值在3.21%～14.93%之间;在灰狼优化算法下,除了砂壤土的目标函数值为0.169 63外,其余土壤目标函数值均在0.001 22～0.009 89之间,11种土壤反演结果的相对误差平均值在2.10%～12.86%之间。分析目标函数值可以发现,目标函数值并不影响反演参数的相对误差。因此,在数值方法中,灰狼优化算法在目标函数3下反演的参数结果优于鲸鱼优化算法。

由于在代数方法中,固定参数θr、θs的鲸鱼优化算法反演效果最好,因此在数值方法中同样考虑固定θr、θs参数值。表4为灰狼优化算法和鲸鱼优化算法在目标函数3下固定θr、θs的反演结果,结果表明:在鲸鱼优化算法下,除了砂壤土和粉质粘壤土的目标函数值分别为0.169 44和0.091 93外,其余土壤目标函数值均在0.000 22～0.002 81之间,反演参数的相对误差平均值在0.45%～15.20%之间;在灰狼优化算法下,除了砂壤土的目标函数值为0.169 44外,其余土壤目标函数值均在0.000 06～0.000 75之间,反演参数的相对误差平均值在0.04%～1.05%之间。因此,在数值方法中,灰狼优化算法固定θr、θs参数值反演土壤参数的值更精确。

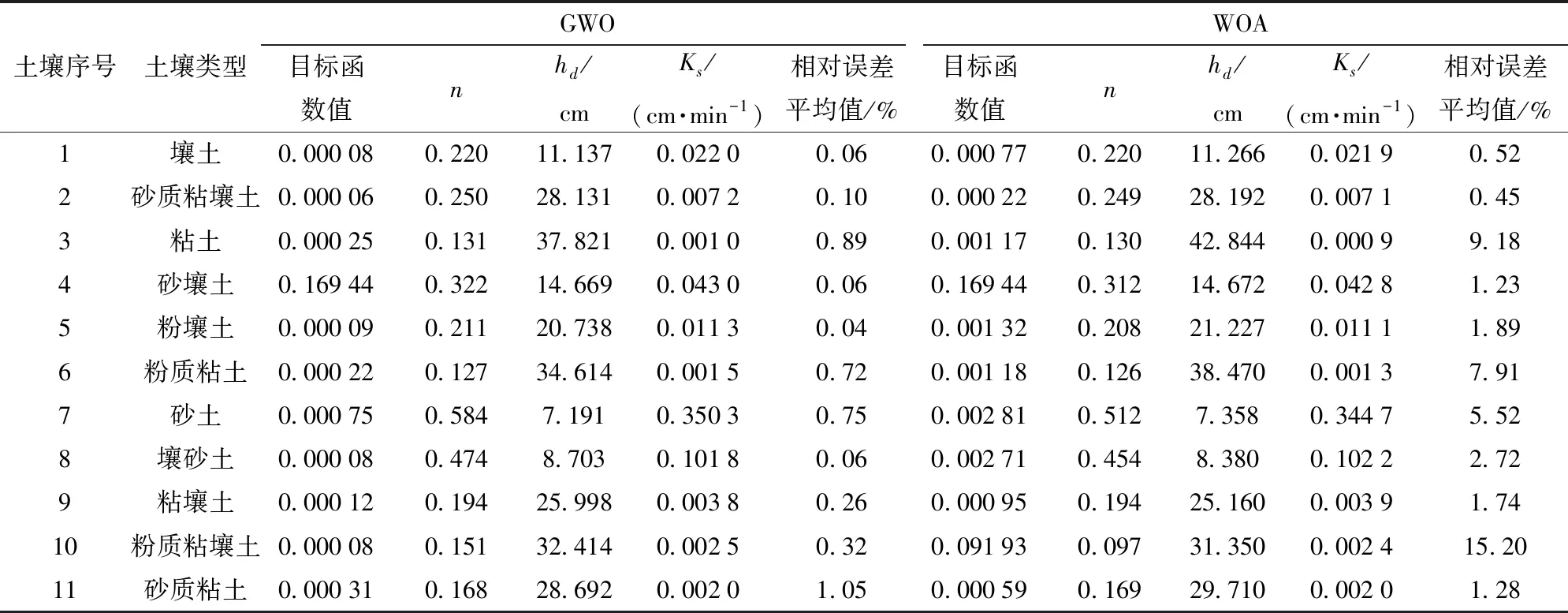
表4 目标函数3下灰狼优化算法和鲸鱼优化算法固定θr、θs反演的参数值

以壤土、砂质粘壤土、粘土、砂壤土为例,将灰狼优化算法在固定参数θr、θs下反演得到的参数代入差分格式中,得到的累积入渗量、入渗率、剖面含水率的数值结果与HYDRUS的结果作比较,比较结果如图7～9(其中,数值解是在固定参数θr、θs下灰狼优化算法针对目标函数3反演得到)所示。从 图7～9 可知,数值解与HYDRUS的结果基本一致,11种土壤的累积入渗量、入渗率、剖面含水率的相对误差都在2.53%以下,决定系数都在0.991 7以上,反演时间为115 s。这表明,灰狼优化算法在目标函 数3下固定θr、θs可以通过数值方法较准确地反演土壤参数。综合分析代数方法与数值方法反演

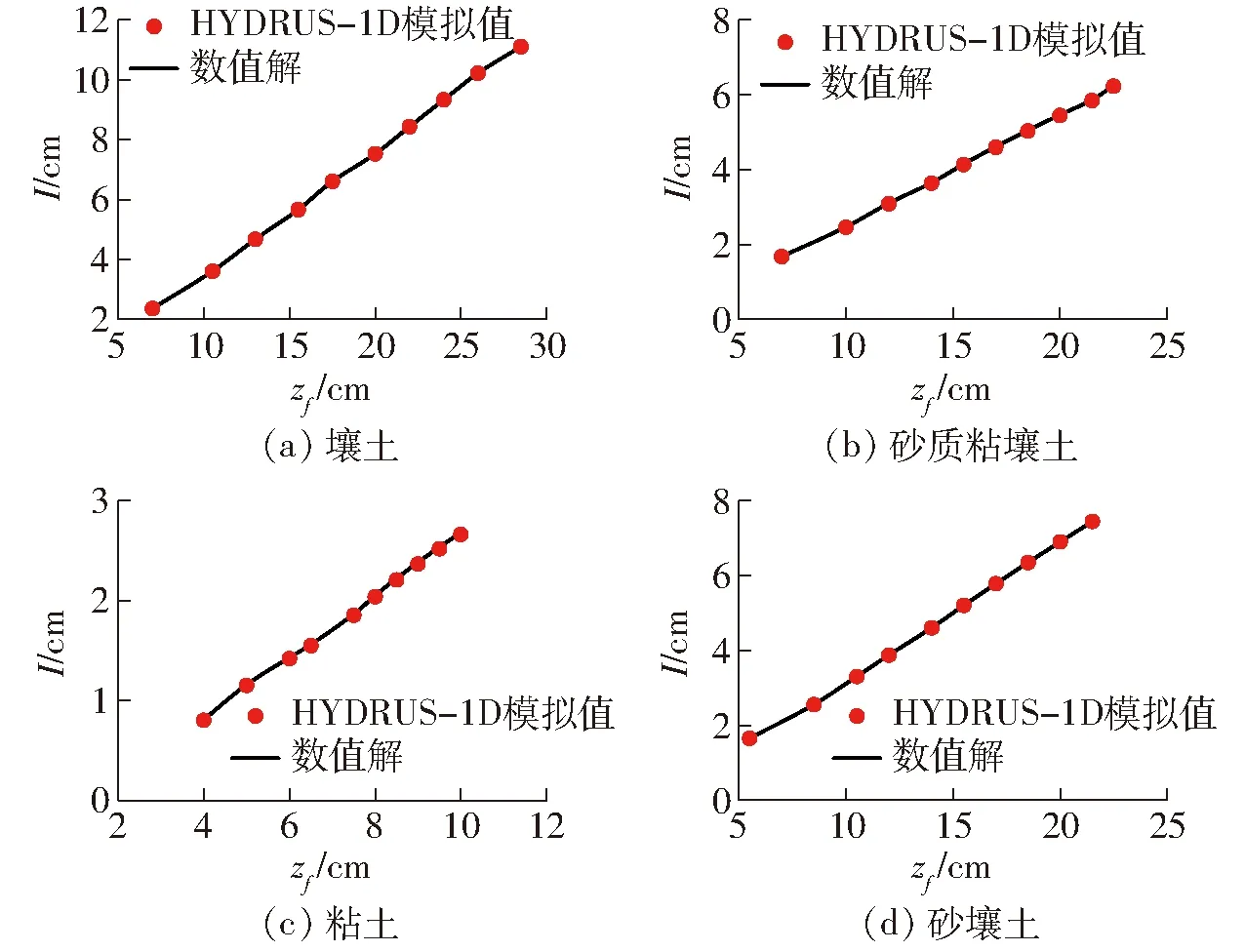
图7 数值方法与HYDRUS-1D模拟得到的累积入渗量对比

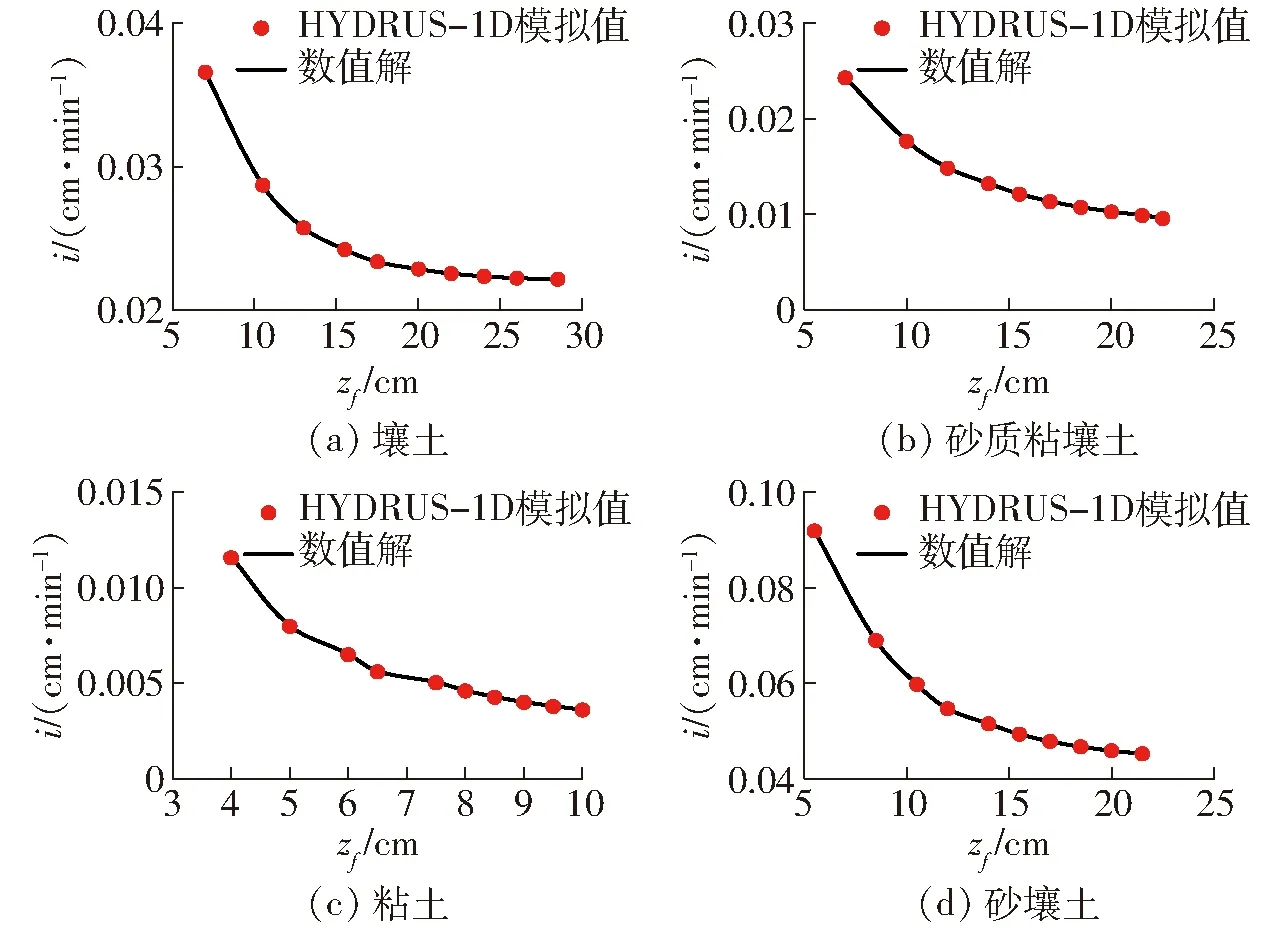
图8 数值方法与HYDRUS-1D模拟得到的入渗率对比

图9 数值方法与HYDRUS-1D模拟得到的土壤剖面含水率对比

结果的相对误差,可知数值方法在固定θr、θs时参数反演的精度比代数方法高。

2.3 方法验证

为评估代数方法和数值方法反演参数的准确性,利用马东豪等[27]的入渗试验数据(陈岗土垂直入渗180 min,如图10所示)进行反演,其中陈岗土的参数θr、θs、hd、n、Ks分别为:0.018 cm3/cm3、0.450 cm3/cm3、68.000 cm、0.297、0.023 0 cm/min。在代数方法与数值方法下固定θr、θs反演参数hd、n、Ks得到的累积入渗量与湿润锋深度、入渗率与湿润锋深度、剖面含水率和湿润锋深度的关系如图10 所示。

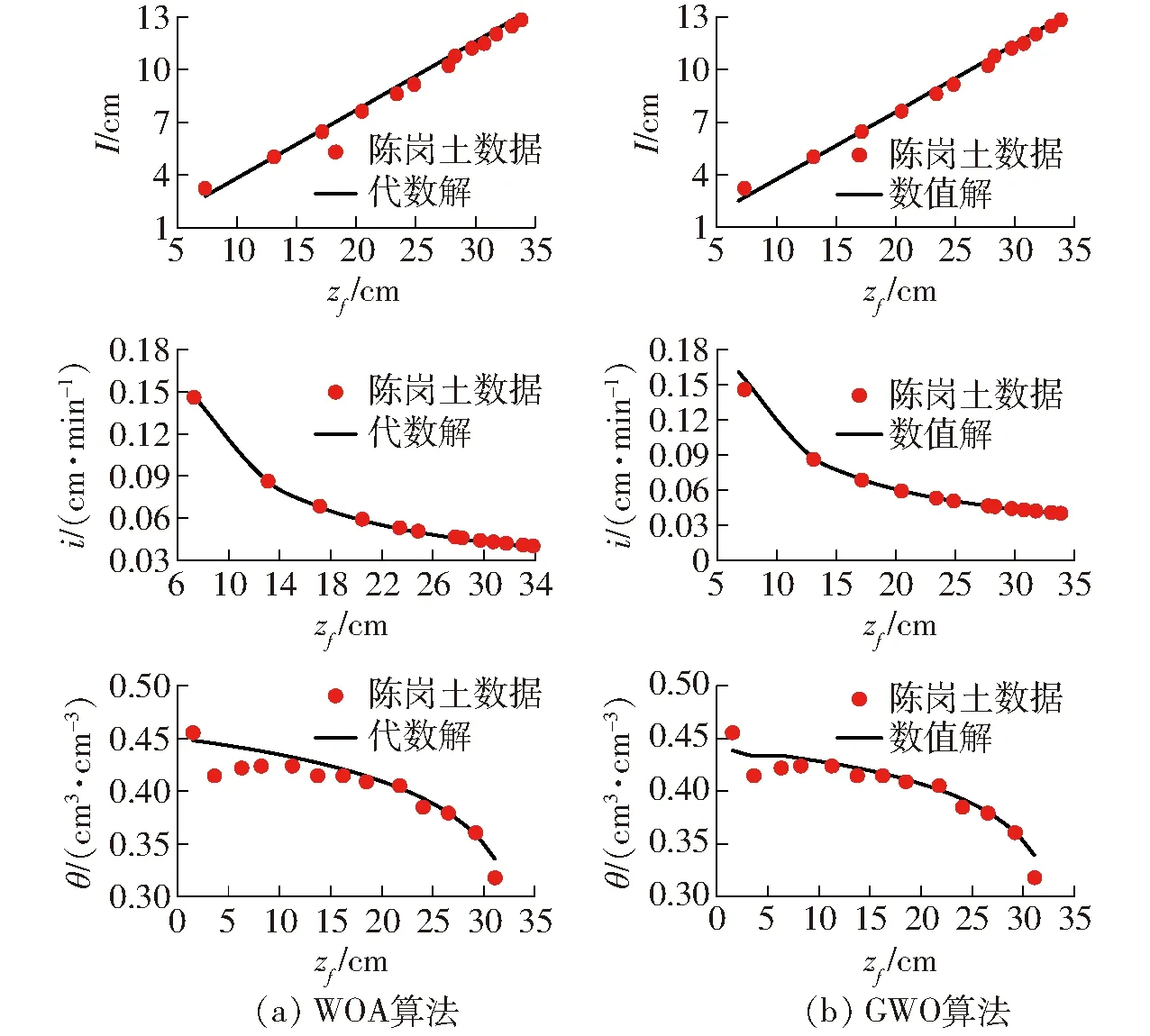
图10 固定θr、θs时代数方法、数值方法反演得到的累积入渗量、入渗率、土壤剖面含水率与实测陈岗土数据对比

在代数方法中,不固定参数时,鲸鱼优化算法反演得到参数θr、θs、hd、n、Ks分别为:0.013 cm3/cm3、0.425 cm3/cm3、61.829 cm、0.147、0.019 2 cm/min,累积入渗量、入渗率、剖面含水率的相对误差分别为4.02%、15.48%、4.17%,决定系数分别为0.982 9、0.860 9、0.840 0;固定参数θr、θs时,鲸鱼优化算法反演得到参数hd、n、Ks分别为:74.524 cm、0.190、0.018 6 cm/min,累积入渗量、入渗率、剖面含水率的相对误差分别为3.30%、1.28%、3.26%,决定系数分别为0.987 5、0.999 1、0.843 3,如图10a所示。

在数值方法中,不固定参数时,灰狼优化算法反演得到参数θr、θs、hd、n、Ks分别为0.016 cm3/cm3、0.427 cm3/cm3、78.622 cm、0.131、0.017 1 cm/min,累积入渗量、入渗率、剖面含水率的相对误差分别为3.46%、5.62%、2.87%,决定系数分别为0.986 3、0.982 8、0.878 4;固定参数θr、θs时,灰狼优化算法反演得到参数hd、n、Ks分别为68.408 cm、0.156、0.020 9 cm/min,累积入渗量、入渗率、剖面含水率的相对误差分别为2.55%、6.63%、2.59%,决定系数分别为0.992 5、0.976 1、0.900 9,如图10b所示。

由式(5)可以看出,当湿润锋深度已知时,累积入渗量主要受到参数θs的影响,因此当累积入渗量的试验数据较为准确时,θs具有较好的反演精度;参数n决定了土壤剖面含水率的形状,且敏感性较高,土壤含水率剖面形状较小差异都会对参数n的反演结果造成较大影响。从图10可以看出,土壤含水率的实测数据变化波动较大,因此,虽然累积入渗量、入渗率和土壤含水率反演误差较小,但代数方法和数值方法对参数n的反演结果均产生了较大误差。

3 结论

(1)代数方法中,采用目标函数2的反演精度优于目标函数1。在目标函数2下,θr未知时,选用鲸鱼优化算法反演θs、hd、n、Ks4个参数;θr已知时,可考虑选用灰狼优化算法反演θs、hd、n、Ks4个参数;θr和θs已知时,可考虑选用鲸鱼优化算法反演hd、n、Ks3个参数,且反演效果最优。

(2)数值方法中,固定参数θr、θs时,灰狼优化算法反演hd、n、Ks3个参数的结果更精确。试验过程中,代数方法的运行时间短,反演一次结果所需的时间大约为70 s,但参数反演的精度低于数值方法;数值方法的运行时间长,但反演精度较高。在实际应用过程中,可以根据不同的需求选择合适的方法。