工况对盾构机主驱动轴承润滑特性的影响*

梁志鹏 程永龙 苏建新

(1.河南科技大学机械工程学院 河南洛阳 471000；2.中铁工程装备集团有限公司 河南郑州 450000)

盾构隧道掘进机(简称盾构机)，是目前隧道施工的核心设备，其国产化率已达到90%以上[1]。而盾构机主驱动轴承是盾构机的三大核心部件之一，目前主要依赖于进口[2]。我国正处于交通工程建设的飞速发展期，在建及规划建设各种隧道超过3万km[3]，盾构机具有广阔的市场前景。因此，盾构机主驱动轴承国产化已成为亟需解决的问题。研究表明，盾构机主驱动轴承在平稳运行状态时，其润滑方式为弹性流体动压润滑，因此对盾构机主驱动轴承进行弹性流体动压润滑研究，可以为主驱动轴承的结构设计和运行状况监测提供理论参考，对提高盾构机主轴承使用寿命和可靠性具有重要意义。

目前，国内外学者针对轴承弹流润滑进行了大量的研究，形成了较为成熟的理论方法。1886年，REYNOLDS[4]提出了Reynolds方程，揭示了流体动压的形成机制，奠定了流体动力润滑的理论基础。1990年，VENNER 等[5]基于多重网格法研究了线接触弹流润滑问题。2005年，VENNER和WIJNANT[6]通过数学模型研究了时变载荷对弹性流体动力润滑的影响。2015年，龙雨诗[7]运用多重网格法对点接触轴承的弹性流体润滑问题进行了研究。2019年，肖少兵[8]研究了温度场对角接触轴承润滑性能的影响。2021年，LIU等[9]基于多重网格法，提出了一种新的压力约束算子对弹流润滑问题进行研究。

综上，轴承弹性流体动压润滑的研究已较为深入，但尚未有基于隧道工程实际工况条件的盾构机主轴承弹流润滑研究的文献。本文作者建立了实际工况条件下的盾构机主轴承弹流润滑模型，采用多重网格法分析不同工况下盾构机主轴承的润滑状态，为盾构机主轴承设计制造及使用维护提供了理论参考。

1 轴承结构及工况条件

以某型号盾构机主驱动轴承为例，其结构如图1所示，包含了3列沿圆周均布的滚子，形成了轴向滚子-滚道接触副(包括主推滚子-滚道接触副、副推滚子-滚道接触副)和径向滚子-滚道接触副。滚子参数如表1所示，滚子和滚道所用材料为GCr18Mo，材料属性如表2所示。轴承所用润滑油为320齿轮油，润滑油参数如表3所示。盾构机主轴承转速为12 r/min。

图1 盾构机主驱动轴承结构简图Fig.1 Structural diagram of main drive bearing of shield machine

表1 某盾构机主驱动轴承滚子参数Table 1 Parameters of main drive bearing roller of a shield machine

表2 某盾构机主驱动轴承材料属性Table 2 Material properties of main drive bearing of a shield machine

表3 润滑油材料属性Table 3 Material properties of lubricating oil

盾构机主驱动轴承主要受轴向力、径向力和倾覆力矩。工作时，主驱动轴承主要受力为轴向推力，分析大量盾构机主轴承磨损数据可知，其主要的磨损接触副为主推滚子-滚道接触副。

以某隧道工程实际测得的轴承受力情况为例，如表4所示，占比99.9%的工况下轴承受力为：轴向力Fa≤24 000 kN，径向力Fr≤9 900 kN，倾覆力矩M≤12 100 kN·m。极限受力工况为：轴向力Fa≤27 000 kN，径向力Fr≤12 000 kN，倾覆力矩M≤15 000 kN·m。

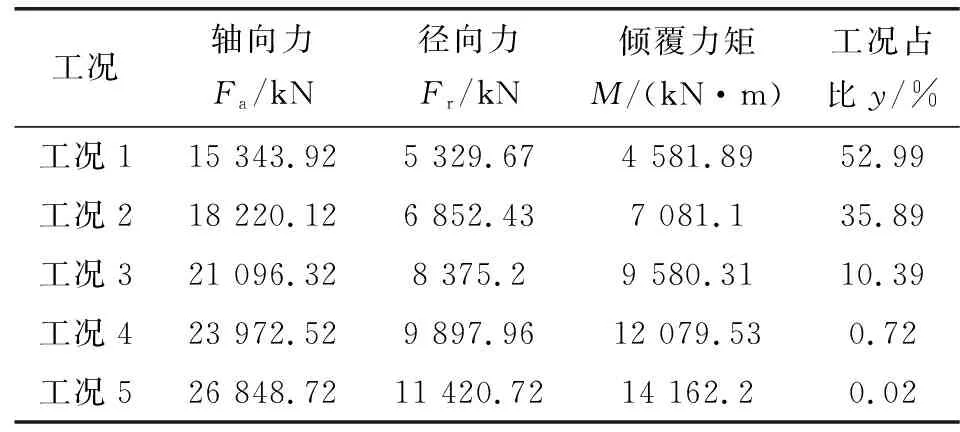
表4 某隧道工程盾构机主驱动轴承载荷分布Table 4 Load distribution of main drive bearing of shield machine in a tunnel project

2 主轴承滚子载荷分布

文中参考文献[10-13]中三排滚子受载计算方法，建立盾构机三排滚子载荷分布模型，对三排滚子载荷分布进行计算，为下一步主驱动轴承润滑特性分析提供载荷参数。

2.1 轴向力作用下的滚子载荷分布

轴向力Fa均匀作用在主推滚子上，其滚子受力Qa为

(1)

式中：Zz为主推滚子数量。

2.2 倾覆力矩下滚子载荷分布

仅考虑倾覆力矩时，将倾覆力矩M等价为偏心轴向力F1和F2(如图1所示)。F1作用于主推滚子，F2作用于副推滚子。

主推滚子在偏心力F2作用下，滚子承受载荷Qz为

(2)

副推滚子在偏心力F2作用下，滚子承受载荷Qf为

(3)

(4)

式中：Qmax为偏心力作用下滚子最大负载；δa为滚子最大接触变形；Dpw为滚子组节圆直径；θ为倾覆力矩作用下内圈倾覆角；φ为滚子位置角；n为载荷-变形系数，取n=9/8。

滚子承载范围角φ为

φ=arccos(1-2ε)

(5)

平衡方程为

F=ZQmaxJa(ε)sinα

(6)

式中：Ja(ε1)和ε1按照2e/Dpw的值再依据文献[10]中给出的关系，利用插值法求得；α为滚子接触角，圆柱滚子取α=90°。

将上述值代入式(5)、(6)分别求得Qzmax、φz然后代入式(2)求得Qz。

同理，将取得的Ja(ε2)和ε2代入式(5)、(6)分别求得Qfmax、φf，然后代入式(3)求得Qf。

2.3 径向力作用下滚子负载

对轴承受力分析可知，径向力主要作用在径向滚子上，则径向滚子负载Qr为

(7)

(8)

式中：Qrmax为径向力Fr作用下滚子最大负载；δr为径向滚子最大接触变形；Gr为滚子径向游隙。

滚子承载范围角φr为

(9)

平衡方程为

Fr=ZrQrmaxJr(ε3)

(10)

不考虑径向滚子径向游隙时，即Gr=0，则由文献[10]中给出的关系，利用插值法求得Jr(ε3)和ε3。代入式(9)、(10)分别求得Qrmax、φr；然后代入式(7)求得Qr。

2.4 滚子受载模型验证

文献[11]中轴承结构与文中相同，其滚子参数见表5。其轴向力为20 000 kN、倾覆力矩为9 700 kN·m、径向力为2 500 kN。验证结果见表6。

表5 文献中盾构机主驱动轴承滚子参数Table 5 Parameters of main drive bearing roller of shield machine in reference

表6 文中模型和文献[11]计算的滚子受载位置及大小比较Table 6 Comparison of the loaded position and size of the roller calculated by the model in the paper and the reference[11]

文中模型误差主要来源于负荷分布积分Ja选取时所用参考文献不同，选取结果有一定误差；同时在计算过程中保留结果的精度有一定的误差。文中主要研究主推滚子的润滑状态，其误差≤1%，误差较小，可应用于滚子受载分析。

2.5 滚子实际载荷

根据受力分析可得到盾构机主驱动轴承的三排滚子负载。其中，主推和副推滚子受轴向力Fa和倾覆力矩共同作用，径向滚子受径向力Fr作用。依据文献[11]中滚子实际载荷分布计算方法，可得到极限工况和99.9%工况条件下三排滚子载荷分布情况如图2所示。180°～360°滚子负载分布情况与0°～180°对称。

图2 极限工况和99.9%工况条件下三排滚子负载Fig.2 Load of three row rollers under extreme working conditions and 99.9% working conditions

经分析可知，盾构机主驱动轴承主推滚子所受载荷远远大于副推滚子及径向滚子，与得到的主轴承主推滚子-滚道磨损最为严重这一分析结果相同。因此，下文主要分析主推滚子-滚道的弹流润滑特性。

3 轴承弹流润滑数学模型

3.1 等温线接触弹流润滑方程

文中建立盾构机主驱动轴承等温线接触弹流润滑数值模型，考虑润滑油黏压方程、密压方程，分析主驱动轴承润滑特性。

(1)Reynolds方程

(11)

量纲一化Reynolds方程：

边界条件为

入口区P(X0)=0

出口区P(Xe)=0，dP(Xe)/dX=0

式中：P为量纲一油膜压力，P=p/pH；p为油膜压力，Pa；pH为最大Hertz接触压力，Pa；X为量纲一坐标，X=x/b，b为Hertz接触半宽，μm；x为卷积速度方向标量。

(12)

其中：

量纲一化膜厚方程：

式中：H为量纲一膜厚，H=hR/b2，h为膜厚，m；R为当量半径，mm；H0为量纲一中心膜厚；E为当量弹性模量，Pa。

(3)黏压方程

(13)

量纲一化黏压方程：

式中：η*为润滑油量纲一黏度，η*=η/η0；η0为常压下的润滑油黏度，Pa·s。

(4)密压方程

(14)

量纲一化密压方程

式中：ρ*为润滑油量纲一密度，ρ*=ρ/ρ0；ρ为润滑油密度，kg/m3；ρ0为常压下的润滑油密度，kg/m3。

1954—2017年全市共报告百日咳病例158 947例，年平均发病率为53.66/10万；死亡298例，年平均死亡率为0.10/10万；病死率为0.19%。在此期间，出现3次报告发病率在200/10万以上的流行高峰，其中1959年为最高峰 （报告发病率为538.13/10万）。

(5)载荷平衡方程

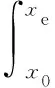
(15)

量纲一化载荷平衡方程：

3.2 数值计算方法

文中采用多重网格法(V循环)求解Reyonlds方程[14]，压力收敛判断准则为

(1)多重网格法

依据文献[15-16]可知，在求解弹流润滑问题时，采用多重网格法全近似格式(FAS)，其第k层网格方程为

LkPk=fk

(16)

式中：Lk为数值算子；Pk为所求解向量；fk为右端项向量，上标k代表网格层的序数。

第k-1层网格方程为

Lk-1Pk-1=fk-1

(17)

其中：

如果第k层网格光滑，则第k+1层网格初始值为

(18)

(2)迭代方法

文中2种迭代方法混合使用，当压力对润滑状态影响远大于膜厚影响时，采用Gauss-Seidel法；当压力影响小于膜厚时，采用Jacobi双极子法。

压力修正方程为

(19)

其中：Gauss-Seidel法δi公式为

Jacobi双极子法δi公式为

计算流程如图3所示。设置初始参数：节点数为129，膜厚方向网格层数为5，起点坐标为-4，终点坐标为1.4。

图3 等温线接触弹流润滑计算流程Fig.3 Calculation flow of isotherm contact elastohydrodynamic lubrication

3.3 弹流润滑模型验证

文献[14]中给定工况参数分别为：载荷176.8 kN，综合弹性模量221 GPa，润滑油黏度0.03 Pa·s，当量接触半径0.02 m，平均速度0.855 m/s，滑滚比0.25。基于上述参数计算轴承的油膜压力和膜厚分布，结果如图4所示。可见文献[14]结果与文中模型结果变化趋势相同，数值存在一定误差，油膜压力最大误差为5.99%，膜厚最大误差为6.54%。两者误差总体在合理范围之内，证明了文中模型的合理性。

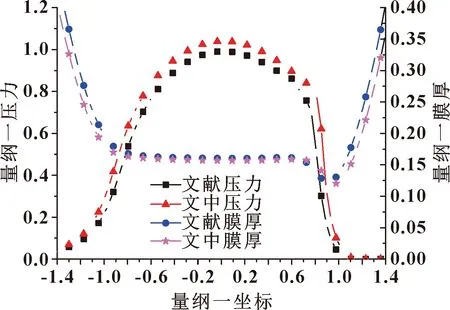
图4 文献[14]与文中模型得到的油膜压力和膜厚比较Fig.4 Comparison of oil film pressure and film thickness obtained in literature[14] and the model in the paper

4 结果分析

4.1 主推滚子弹流润滑特性

盾构机主驱动轴承主推滚子最大负载如表7所示。随着盾构机主驱动轴承受力的增大，主推滚子最大负载也在增大。

表7 不同工况条件下主推滚子最大负载 单位：kNTable 7 Maximum load of main push roller under different working conditions Unit：kN

99.9%工况和极限工况下轴承的油膜压力和膜厚分布如图5所示。

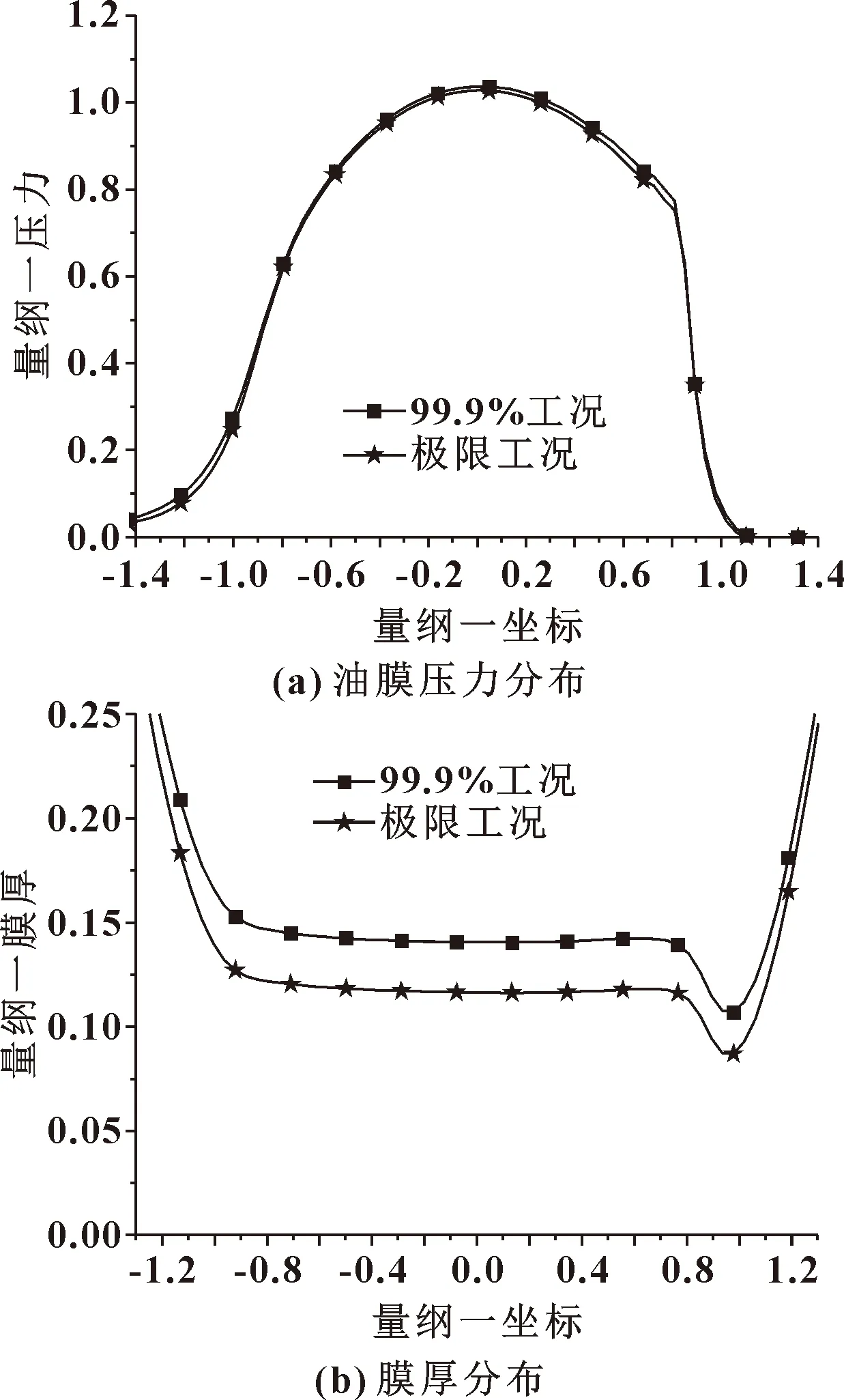
图5 极限工况和99.9%工况下主推滚子油膜压力和膜厚分布Fig.5 Distribution of oil film pressure(a)and film thickness (b)of main push roller under extreme working condition and 99.9% working condition

由图5(a)可知，在极限工况下油膜压力分布曲线先上升然后下降，二次峰值不明显，趋于光滑；99.9%工况条件下油膜压力分布趋势相同，但二次峰值较为明显。由图5(b)可知，极限工况下膜厚分布曲线先下降然后趋于平稳，最后上升，突变较为明显；99.9%工况条件下油膜压力分布趋势相同。可见，2种工况条件下轴承润滑特性变化趋势相似，其整体数值差别较小。

图5中极限工况下量纲一最大油膜压力和最小膜厚值分别为1.028和0.087，99.9%工况条件下量纲一最大油膜压力和最小膜厚值分别为1.037和0.107。量纲一化最大油膜压力差约为0.009，其差值相对较小。量纲一化最小膜厚差约为0.020，其数值差别较大。

4.2 不同工况下润滑特性分析

在实际测得的工况条件下的滚子位于最大负载处的量纲一油膜压力和膜厚分布如图6所示。结果表明，随着盾构机主驱动轴承所受轴向力、径向力及倾覆力矩的增大，油膜压力和油膜厚度在逐渐减小，但是其变化趋势相同。从图6(a)可以看出，油膜压力受轴承受力变化的影响较小；不同工况条件下油膜压力曲线均先上升然后下降，二次峰值较明显。

图6 不同工况下主推滚子油膜压力及膜厚分布Fig.6 Distribution of oil film pressure(a)and film thickness(b) of main push roller under different working conditions

从图6(b)可以看出，油膜厚度受轴承受力变化的影响较大，且受力越大，膜厚越小；不同工况条件下膜厚变化曲线一致，均为先下降再趋于平稳然后上升，且均产生突变。

4.3 不同滚子位置下润滑特性分析

不同工况条件下不同位置的主推滚子负载分布如图7所示，不同工况条件下主驱动轴承量纲一最大油膜压力和最小膜厚随滚子位置变化情况如图8所示。

图7 不同工况下不同位置主推滚子负载分布Fig.7 Load distribution of main push roller at different positions under different working conditions

图8 不同工况下不同位置主推滚子的最大油膜压力和最小膜厚分布Fig.8 Distribution of maximum oil film pressure(a)and minimum film thickness(b)of main push roller at different positions under different working conditions

结果表明，随着盾构机主驱动轴承主推滚子位置由0°转动到180°，滚子负载在逐渐变小，而滚子量纲一最大压力和最小膜厚在逐渐变大；两者均在滚子负载最大处取得最小值，在滚子负载最小处取得最大值；滚子处于相同位置时，两者均随着盾构机所受径向力、轴向力和倾覆力矩的变大而减小。

5 结论及展望

建立实际工况条件下的盾构机主驱动轴承等温线接触弹流润滑模型，并分析了某隧道工程实际工况下主驱动轴承的润滑特性。主要结论如下：

(1)不同工况条件下盾构机主轴承主推滚子油膜压力和膜厚变化情况相同，均出现二次峰值；工况条件对油膜压力影响较小，对膜厚影响较大，且二者均随受力的增大而减小。

(2)滚子位于不同位置时的最大油膜压力和最小膜厚与滚子负载变化情况相反，在滚子位于负载最大位置时二者均为最小值，而滚子位于负载最小位置时，二者均为最大值；滚子位于相同位置时，二者最值均随着盾构机主驱动轴承受力的增大而减小。

上述研究表明，盾构机主驱动轴承在实际工作中，受力越大对其润滑特性影响越大，可以作为隧道地质情况选择时的参考依据，同时可以为实际施工时主轴承润滑状态监测提供理论参考。另外，文中的计算结果仅是局部约束条件下简化模型的计算结果，只能反映其润滑特性规律，不能真实反映整个盾构机主驱动轴承实际工况条件下的润滑特性；同时，文中未考虑运行过程中主轴承温度变化情况及温度变化对油膜压力及膜厚的影响。下一步需要针对上述问题进行深入的研究，以准确反映主轴承润滑特性。