基于Carreau流变模型的圆柱滚子轴承热混合润滑分析*
何文卓 刘晓玲 朱鹏娟 周亚林
(青岛理工大学机械与汽车工程学院 山东青岛 266520)
圆柱滚子轴承是最为常见的滚子轴承,其主要特点是负荷能力大、摩擦因数小、回转精度高,被广泛应用于各类低速重载工况下的大型设备中。随着机械设备向着高速、重载的方向发展,轴承的工作条件也越来越恶劣,使得实际工况中润滑油往往呈现出显著的非牛顿特性[1-2]。CUPU等[3]基于Power Law流变模型研究稳态等温线接触条件下轴承性能参数变化对压力和膜厚的影响。尹昌磊等[4]基于Newton和Ree-Eyring流体,对线接触等温和热弹流润滑进行了数值分析,研究了润滑油的流变性对线接触弹流润滑油膜黏度的影响,以及在不同滑滚比下压力、膜厚及温度的分布规律。上述研究均表明润滑油的剪切稀化行为对轴承接触表面润滑摩擦特性的影响不可忽略。
近些年来,以Carreau为代表的幂函数流变模型逐渐兴起,人们发现该流变模型更能反映弹流润滑的油膜特征,因此对于Carreau流变模型的研究越来越广泛[5]。刘剑平等[6]采用Carreau流变模型和Ree-Eyring流变模型,对线接触弹流润滑进行了数值分析,结果表明与Ree-Eyring流变模型相比,Carreau流变模型的理论分析结果更能反映剪切稀化流体的实际弹流油膜厚度,并且幂函数形式的流变模型更能反映剪切稀化流体的流变特性。杨萍等人[7]在Carreau流变模型的基础上,推导出了新的幂函数流变模型,并进行了热弹流润滑分析。
上述对接触表面弹流润滑的研究虽考虑了润滑油的非牛顿特性,但假设接触副表面是光滑的,并没有考虑表面粗糙度的影响,而表面粗糙度会对润滑状态产生重要影响,甚至会导致润滑失效。且在实际工程中,轴承的接触副大都处于混合润滑状态。对于其混合润滑的研究,REN等[8]提出了考虑粗糙表面的三维线接触混合润滑模型。ZHU等[9]基于确定性模型改进了线接触混合润滑模型,针对轴承等关键传动零部件,考虑了表面粗糙度等工程实际问题。周江敏等[10]研究了表面粗糙度及热效应对非牛顿混合润滑的影响,基于平均流量模型,考虑表面粗糙度以及热效应,建立线接触非牛顿混合润滑模型,探讨了表面粗糙度对膜厚、膜厚比、平均摩擦因数、载荷比及温度分布的影响,并与等温解进行比较。
综上所述,已有对接触表面润滑的研究多基于Ree-Eyring非牛顿流体,因此,本文作者基于Carreau流变模型,考虑表面粗糙度的影响及轴承实际的混合润滑状态,求解非牛顿流体热混合润滑问题,探讨滑滚比、卷吸速度和载荷对轴承润滑特性的影响,并与牛顿流体数值解进行对比,为进一步优化轴承参数提供润滑理论依据。
1 数值计算模型
1.1 圆柱滚子轴承运动分析
图1所示为轴承的结构示意图[11-12]。图中,ω为内圈角速度,ωj为滚子自转角速度,ωc为保持架的角速度,Di为内滚道直径,Do为外滚道直径,Dm为节圆直径,Dr为滚子直径,Fr为径向载荷,Qo为受载滚子最大法向载荷,φj为受载滚子中心线与径向载荷作用线之间的夹角,Qj为φj位置上滚子所受的法向载荷。
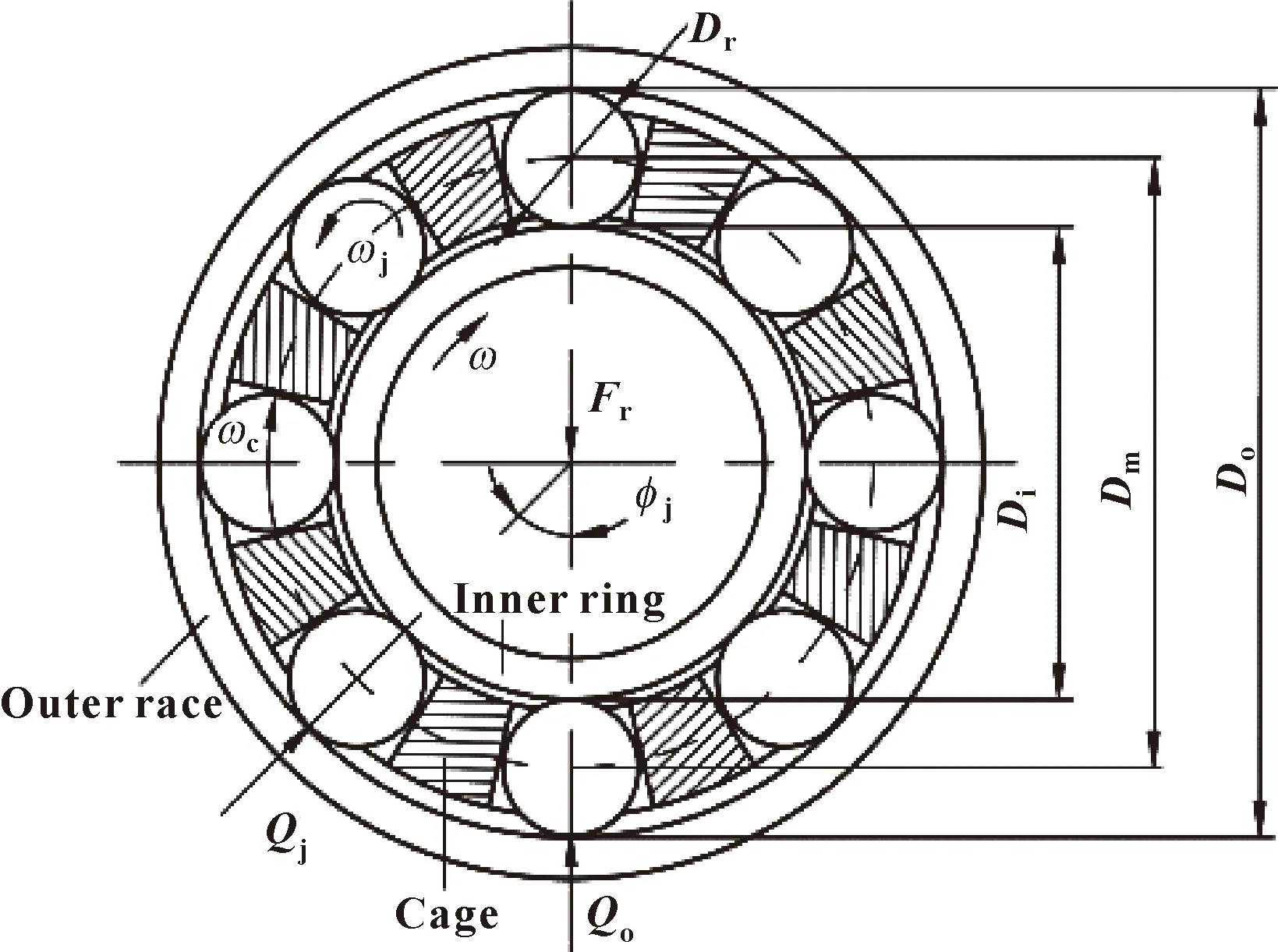
图1 轴承结构示意Fig.1 Schematic of cylindrical roller bearing
轴承外圈固定,内圈转动。假设圆柱滚子轴承做匀速运转,其中,滚子的速度为
(1)
内圈的速度为
(2)
圆柱滚子与内圈的接触副可以等效为图2所示2个圆柱的线接触模型,u1、u2为两接触表面的切向速度(m/s),曲率半径分别为R1、R2。当量半径R与曲率半径R1、R2的几何关系为
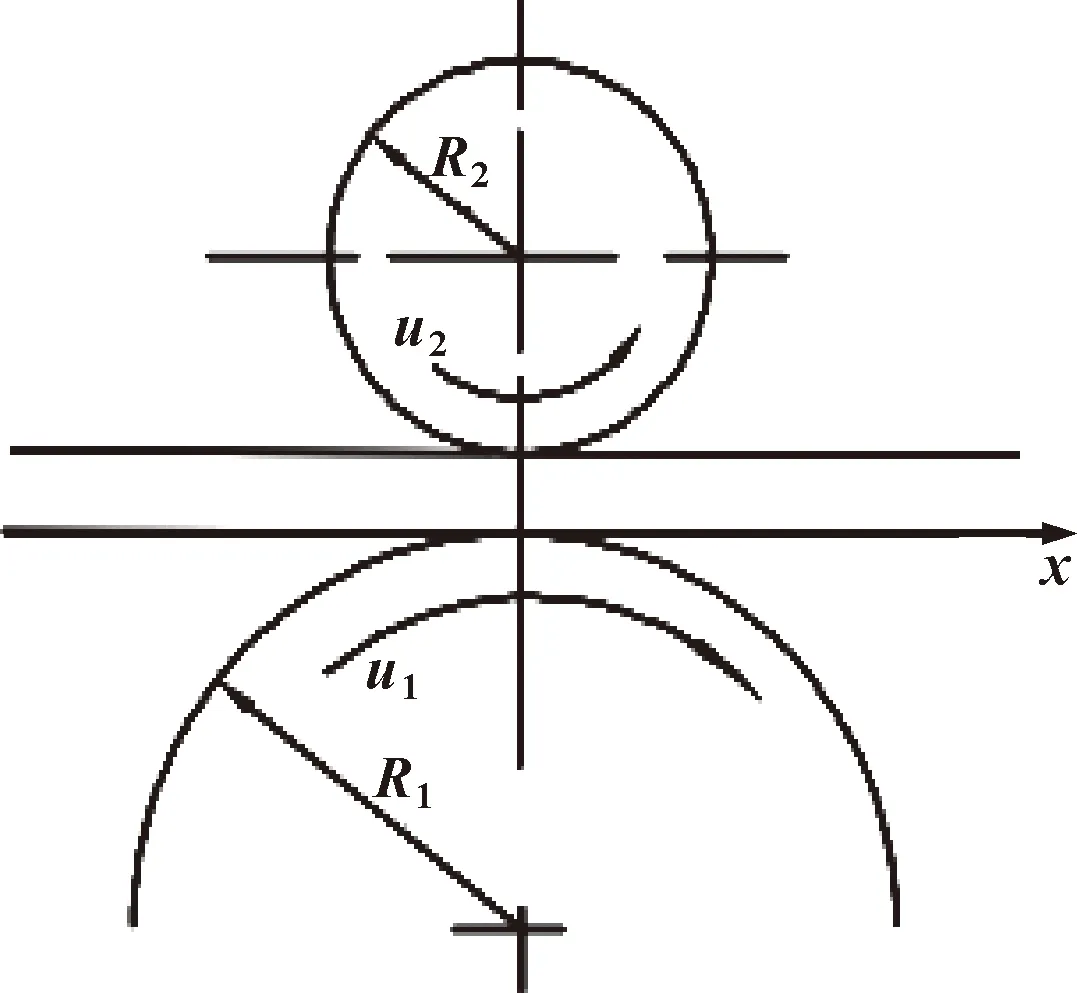
图2 几何关系Fig.2 Geometric relation
(3)
1.2 混合润滑基本方程
采用Carreau流变模型[5],等效黏度方程为
(4)
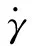
在全膜润滑时载荷由油膜承担,而在混合润滑时,粗糙峰和润滑油膜共同承载[13],所以总压力p是油膜压力ph与粗糙峰压力pa之和:
p=ph+pa
(5)
文中,粗糙峰接触压力pa、接触副的摩擦力F及平均摩擦因数fc的表达式和文献[10]一致。
图3所示是粗糙表面接触模型,u1、u2是固体1、2的运动速度,ht表示实际油膜厚度,h表示2个粗糙表面中线构成的名义膜厚。

图3 粗糙表面接触模型Fig.3 Rough surface contact model
(1)Reynolds方程
由Patir和Cheng平均流量模型[14],推导出广义平均Reynolds方程:
(6)
其中:
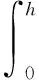
式中:φx为压力流量因子;ue为卷吸速度,ue=(u1+u2)/2;hT为两固体表面的平均间隙;ρ为润滑油的密度。
hT的表达式[15]可写为
(7)
压力流量因子φx的表达式[14]为
(8)
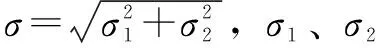
广义平均Renynolds方程的边界条件为
(9)
式中:xin、xout表示计算域的边界。
(2)密压密温、黏压黏温关系
用Tait状态方程[16]描述润滑油的密压密温关系
[1-ε(T-T0)]
(10)

黏压黏温关系[16]
(11)
式中:η0为润滑油环境黏度(Pa·s);V是流体质点体积(m3);V0为环境体积;Vocc为占有体积;B是无量纲常数。
(3)载荷平衡方程
载荷平衡方程的表达式为
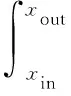
(12)
载荷比的表达式为
(13)
(4)油膜名义厚度
油膜名义厚度h由下式求得:
(14)
式中:h00表示两表面的变形量;R为两固体的综合曲率半径;E′为两固体的综合弹性模量。
(5)能量方程
温度T可由油膜能量方程求得:
(15)
式中:c表示润滑油的比热容;k表示润滑油的热传导系数;u表示油膜流速;Qa是由粗糙峰引起的单位体积热量。
(16)
式中:us表示2个粗糙峰接触时的滑动速度,us=|u1-u2|;fa表示粗糙峰接触时的摩擦因数。
(6)固体热传导方程
固体1、2的能量方程:
(17)
式中:c1、c2分别表示固体1、2的比热容;ρ1、ρ2分别表示固体1、2的密度;k1、k2分别表示固体1、2的热传导系数。
固体1、2表面满足如下的热流量连续条件:
(18)
2 数值方法

在数值计算中,采用多重网格法求解油膜压力,采用多重网格积分法求解膜厚方程中的弹性变形,采用逐列扫描法求解油膜温度。网格层数为6,最高层网格节点数为961个节点。压力和温度的收敛精度为1×10-4,载荷的收敛精度为1×10-3。程序的计算采用文献[17]的方法,如图4所示。其中,ω1、ω2、ω3分别为压力、膜厚和温度松驰因子。
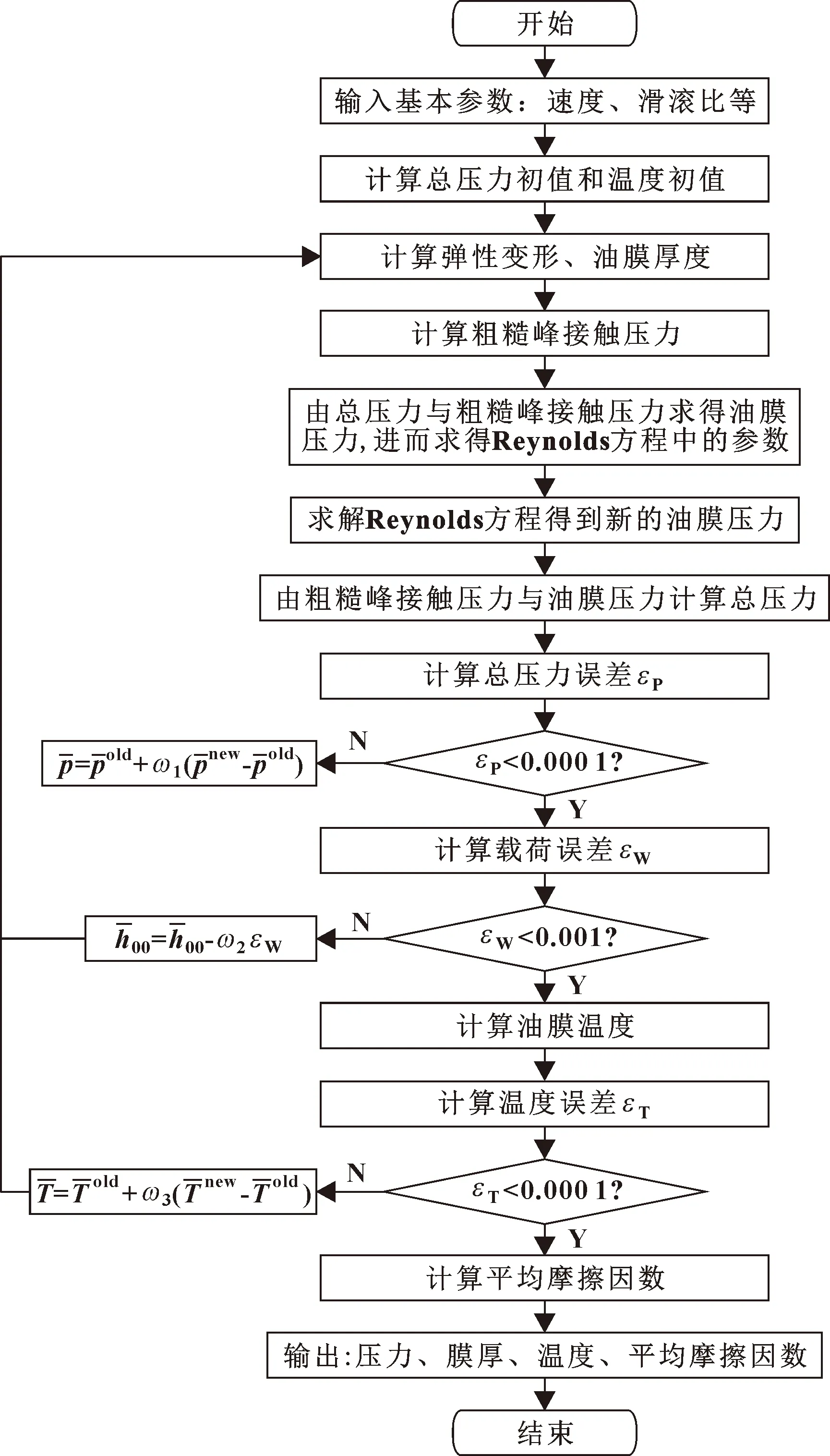
图4 计算程序流程Fig.4 Flow of calculation program
3 计算结果及分析
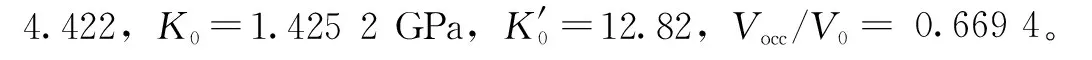

表1 润滑油参数Table 1 The parameters of lubricating oil
滑滚比定义为ζ=(u1-u2)/ue,在ζ=0.05、W=1×10-4(pH=0.91 GPa)、Ue=1×10-11时,得到了Carreau流变模型的热混合润滑条件下的压力、膜厚,并与相同工况下的牛顿流体进行了比较,如图5所示。可以看出,Carreau流变模型在混合润滑状态下的压力与牛顿流体的差别很小,膜厚略低于牛顿流体。
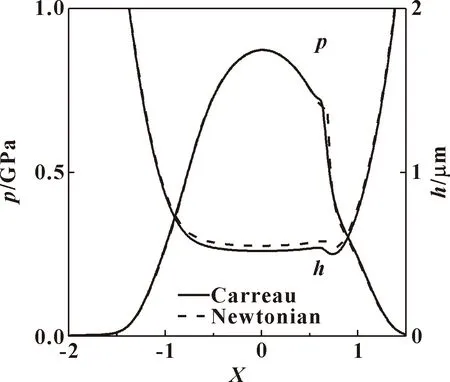
图5 Carreau非牛顿流体与牛顿流体压力及膜厚的 比较(ζ=0.05,W=1×10-4,Ue=1×10-11)Fig.5 Comparisons of pressure and film thickness between Carreau non-Newtonian and Newtonian fluids for ζ=0.05,W=1×10-4 and Ue=1×10-11
3.1 滑滚比的影响
在W=1×10-4、Ue=5×10-11条件下,基于轴承实际,选取较小滑滚比,且滑滚比在0.00~0.08之间变化,求解在混合润滑状态下,不同滑滚比时Carreau非牛顿流体的油膜最高温度、最小膜厚、平均摩擦因数等参数,并与牛顿流体数值解进行对比。如图6所示。
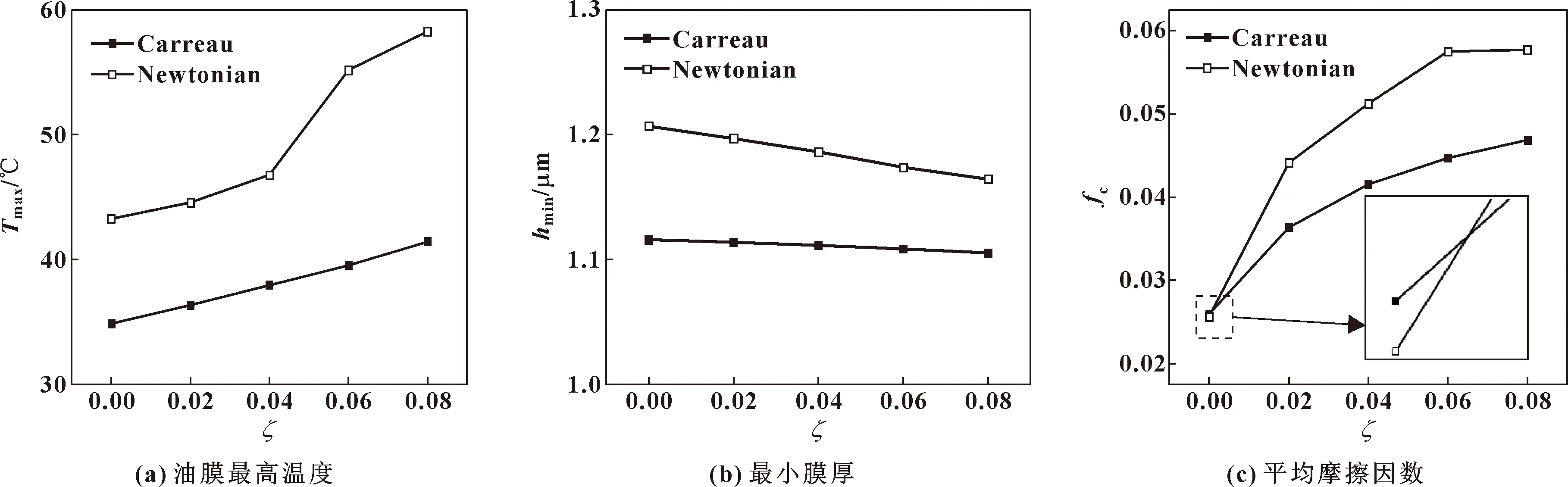
图6 不同流变模型油膜最高温度、最小膜厚和平均摩擦因数随滑滚比变化的趋势Fig.6 Variations of maximum film temperature(a),the minimum film thickness(b),and average friction coefficient(c)with slide-roll ratio in different rheological models
图6(a)给出了在不同滑滚比下,Carreau非牛顿流体和牛顿流体油膜最高温度的变化。可知,随着滑滚比的增加,Carreau非牛顿流体和牛顿流体最高油膜温度均增加,主要是因为随着滑滚比的增加,剪切发热增加,逐渐取代了压缩功在热效应中的主导作用。同时,Carreau非牛顿流体中的剪切发热要低于牛顿流体剪切发热,因此,Carreau非牛顿流体油膜温度要低于牛顿流体油膜温度。由图6(b)可知,最小膜厚都随着滑滚比的增大而减小,主要是因为压缩功和剪切热的存在而导致的油膜温度升高,黏度降低,膜厚变薄。在小滑滚比下,Carreau非牛顿流体最小膜厚低于牛顿流体的最小膜厚,且减小的趋势与牛顿流体相比较为平缓。由图6(c)可知,当滑滚比ζ=0时,Carreau非牛顿流体与牛顿流体平均摩擦因数相差较小。随着滑滚比的增大,平均摩擦因数也在增大。这是由于界面滑动速度的增加导致油膜厚度降低,使剪切应力增大,总的摩擦力增大,载荷不变,因此平均摩擦因数增大。
3.2 卷吸速度影响
在上述模型中,滚子与内圈的平均速度可视为卷吸速度。在ζ=0.05、W=1×10-4条件下,卷吸速度在0.2~1.0 m/s之间变化,求解混合润滑状态下不同卷吸速度时的数值解,并将油膜最高温度、膜厚比λ(λ=hmin/σ)、载荷比与牛顿流体数值解进行对比。
图7所示为压力随卷吸速度的变化。可看出在载荷一定时,随着卷吸速度的增大,油膜压力ph逐渐增大,固体接触压力pa逐渐减小,总压力p变化不大。
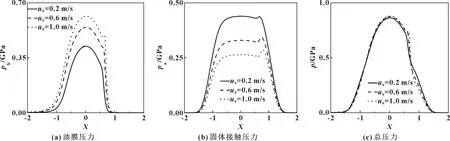
图7 Carreau非牛顿流体压力随卷吸速度变化的趋势(ζ=0.05,W=1×10-4)Fig.7 Variations of Carreau non-Newtonian fluid pressure with entrainment velocity for ζ=0.05 and W=1×10-4:(a)oil film pressure;(b)asperity pressure;(c)total pressure
图8给出的是油膜厚度随卷吸速度变化的趋势。可以看出随着卷吸速度的增大,油膜厚度明显增大。卷吸速度越小,润滑膜厚越小,这是因为剪切变稀的非牛顿性使得流体的黏度随着剪应变率的提高而变小,要承受同样的载荷,润滑剂的膜厚需要变得更薄来增加承载能力。
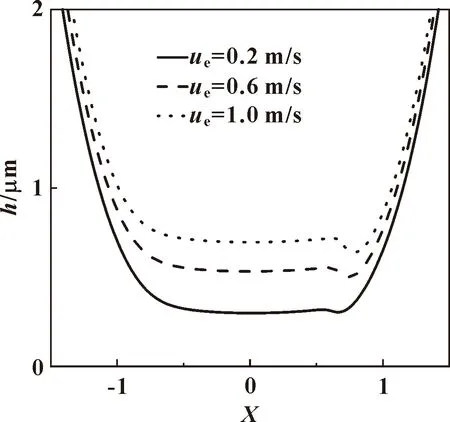
图8 Carreau非牛顿流体油膜厚度随卷吸速度变化的趋势(ζ=0.05,W=1×10-4)Fig.8 Variations of oil film thickness of Carreau non-Newtonian fluid with entrainment velocity for ζ=0.05 and W=1×10-4
图9(a)给出了不同卷吸速度下,2种流体油膜最高温度的变化。可知,非牛顿流体最高油膜温度整体上低于牛顿流体;在卷吸速度较小时,两者温度差值不大,在卷吸速度较大的时候,两者的差值逐渐增大,且都随着卷吸速度的增大而增大,这是因为随着卷吸速度的增大,对润滑油的压缩和剪切使得润滑油的温度明显上升。由图9(b)可知,膜厚比随着卷吸速度的增大而增大,而且增大的趋势基本相同。又因为σ不变,所以它们的膜厚也在增大。当卷吸速度较小时,两者的膜厚比没有太大的差别。由图9(c)可知,随着卷吸速度的增大,两者的载荷比逐渐减小。这是因为两者的膜厚都在增大(见图9(b)),这让接触的粗糙峰变少,粗糙峰承受的载荷减小,总载荷不变,从而载荷比也在变小。又因为非牛顿流体的膜厚整体上小于牛顿流体的膜厚,所以它的载荷比要大于非牛顿流体的载荷比。2种流体膜厚变化的趋势大致一样,使得载荷比的变化趋势也大致相同。
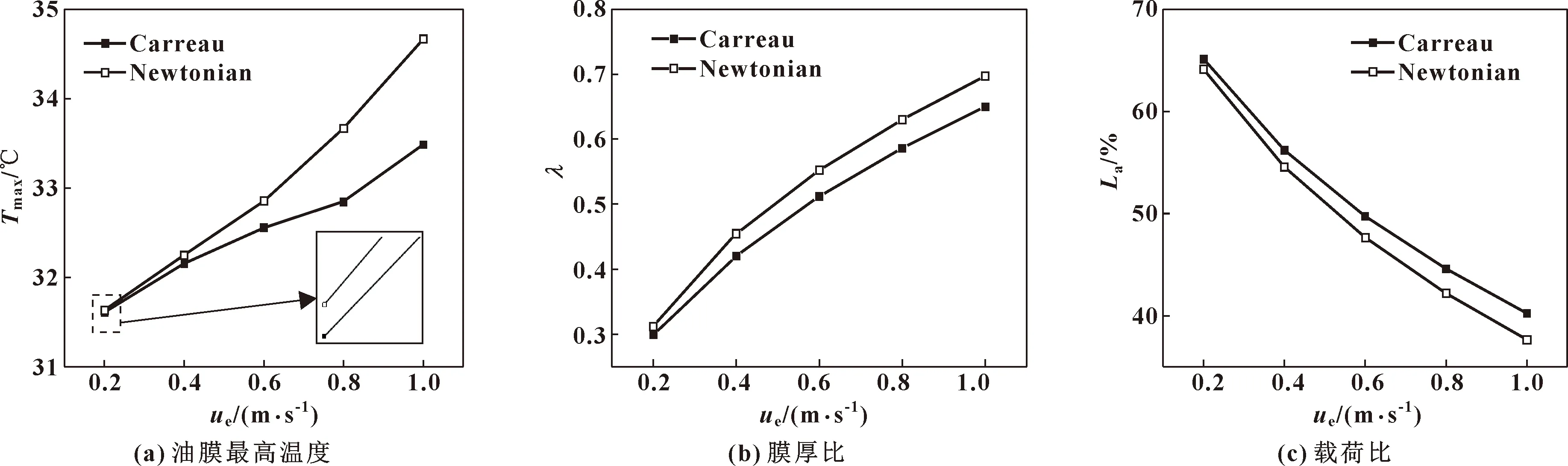
图9 不同流变模型油膜最高温度、膜厚比和载荷比随卷吸速度变化的趋势Fig.9 Variations of oil film maximum temperature(a),film thickness ratio(b),and the load ratio(c)with entrainment speed in different rheological models
3.3 载荷影响
由Hertz接触理论可知,接触区的载荷与最大Hertz压力有关,因此文中考虑最大Hertz压力的影响,在ζ=0.05、Ue=2×10-11条件下,求解最大Hertz压力在0.3~1.8 GPa之间变化时混合润滑状态下不同载荷时的数值解,并将油膜最高温度、膜厚比、载荷比与牛顿流体数值解进行对比。
图10所示为总压力p、油膜压力ph及固体接触压力pa随最大Hertz压力的变化趋势。可知随着最大Hertz压力的增大,三者都逐渐增大。
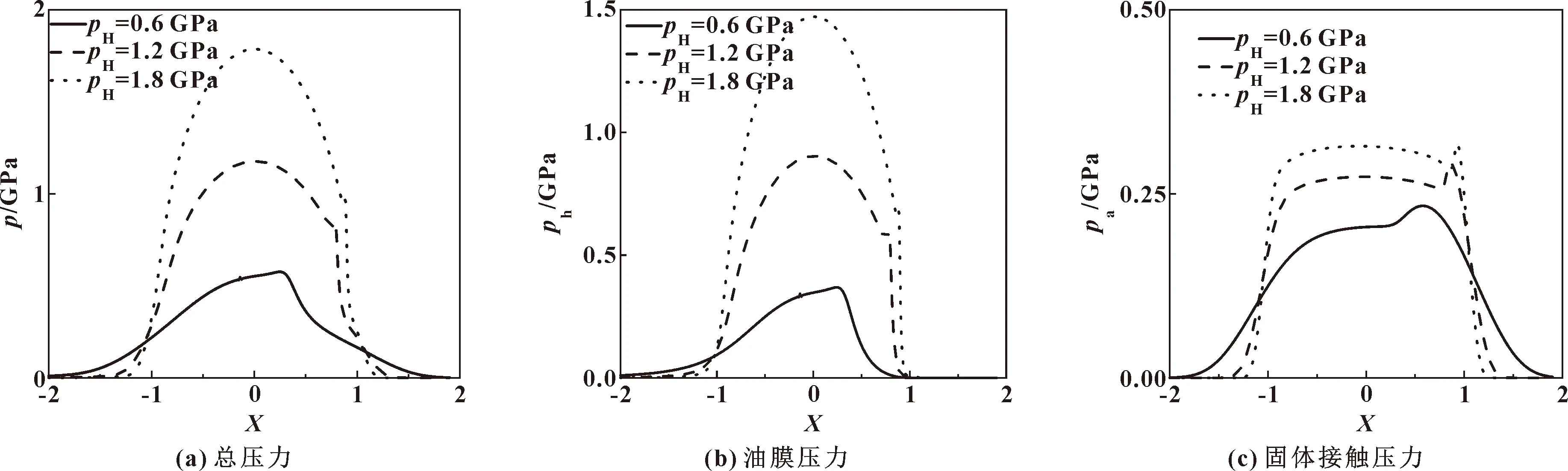
图10 Carreau非牛顿流体压力随最大Hertz压力变化的趋势(ζ=0.05,Ue=2×10-11)Fig.10 Variations of Carreau non-Newtonian fluid pressure with maximum Hertzian pressures for ζ=0.05 and Ue=2×10-11:(a)total pressure;(b)oil film pressure;(c)asperity pressure
图11给出的是油膜厚度随最大Hertz压力变化的趋势。可以看出随着最大Hertz压力的增大,油膜厚度逐渐减小,这是为了承受更多的载荷。

图11 Carreau非牛顿流体油膜厚度随最大Hertz压力变化的趋势(ζ=0.05,Ue=2×10-11)Fig.11 Variatione of oil film thickness of Carreau non Newtonian fluid with maximum Hertzian pressures for ζ=0.05 and Ue=2×10-11
图12(a)给出了最高油膜温度随最大Hertz压力的变化。可以看出,当最大Hertz压力较小时,2种流体的油膜温度相差不大。在最大Hertz压力变大的过程中,两者的差值逐渐增大,而且牛顿流体油膜温度上升趋势更为明显。由图12(b)可知,膜厚比都随着最大Hertz压力的增大而减小,而且最大Hertz压力对2种流体膜厚比的差值没有太大的影响。当最大Hertz压力较小时,两者的膜厚比没有太大的差别。由图12(c)可知,随着最大Hertz压力的增大,两者的载荷比逐渐减小。这是因为在混合润滑中,总载荷由油膜和粗糙峰共同承担,随着最大Hertz压力的增大,油膜压力和固体接触压力都在增大,油膜压力增大的幅度远高于固体接触压力增大的幅度(如图10所示),这使得粗糙峰承受的载荷在总载荷中占比减小,因此载荷比也变小。同时Carreau非牛顿流体的膜厚整体上小于牛顿流体的膜厚,粗糙峰承受的载荷更多,所以它的载荷比要大于牛顿流体的载荷比。
4 结论
(1)在圆柱滚子轴承中,随着滑滚比的增大,油膜温度整体上升,膜厚下降趋势平缓,平均摩擦因数增大,与牛顿流体相比,Carreau非牛顿流体的油膜温度、膜厚及平均摩擦因数都较小。
(2)随着卷吸速度的增大,油膜压力上升,固体接触压力下降,使得载荷比减小;而随卷吸速度的增大,油膜温度和膜厚比上升;Carreau非牛顿和牛顿流体的膜厚比和载荷比的变化趋势相似。
(3)随着最大Hertz压力的增大,油膜压力和固体接触压力都在升高,油膜压力上升的幅度比固体接触压力上升的幅度大,使得载荷比下降;而随最大Hertz压力的增大,油膜温度增大,膜厚比减小。2种流体的膜厚和载荷比随最大Hertz压力的变化趋势大致相同。

