一题“多”解 多解归“一”——从一道矩形的翻折问题谈起

文／金明

矩形的翻折问题一直是中考压轴题的高频考点，同学们遇到这类问题时常常无法将已知条件和数学知识建立联系，更不知从哪方面入手。现借助一道矩形内翻折问题的变式拓展，帮助同学们熟悉相关数学模型。

例题 如图1，在矩形ABCD中，AB=4，BC=6，点E为BC的中点，将△ABE沿AE折叠，使点B落在矩形内的点F处，连接CF，求CF的长。

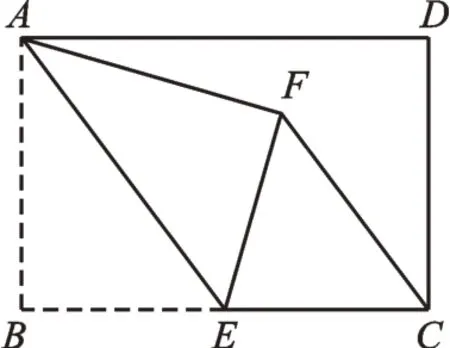
图1

【分析】由EF=EC=EB可构造出直角三角形BFC，即将求线段CF的长转化为“解直角三角形”。连接BF交AE于点K，如图2，由“翻折”的性质得到垂直，再由已知直角（∠ABE=90°）得到常见的“母子相似模型”（∠ABE=∠BKA=90°），其常用的结论是“三组直角三角形相似”和“角的等量关系”。本题也可以利用△ABE∽△BFC进行求解，或利用中位线先求KE，再求CF。

【简解】如图2，连接BF交AE于点K。

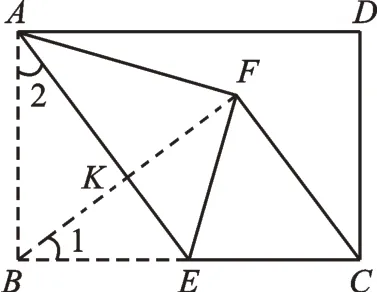
图2

变式1 如图3，连接BF并延长，交线段AD于点G，求线段FG的长。

图3

变式2 如图4，延长EF交线段AD于点G，求线段FG的长。

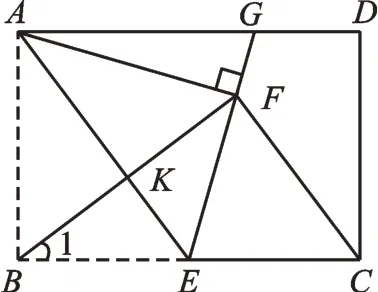
图4

【分析】变式2的出发点是想让同学们体会“角平分线”“平行”“等腰三角形”在矩形翻折问题中的应用，这里称之为“平行+角平分线模型”。当然，除此之外还有其他不同的方法。

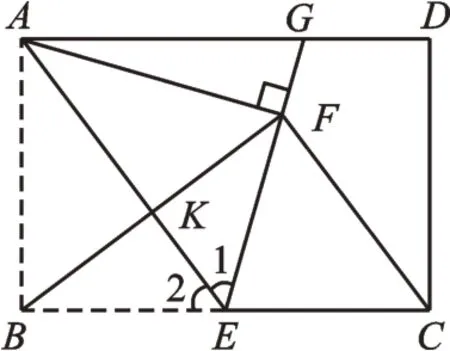
图5

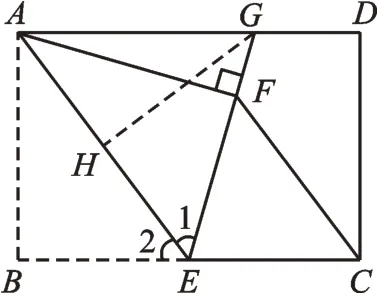
图6

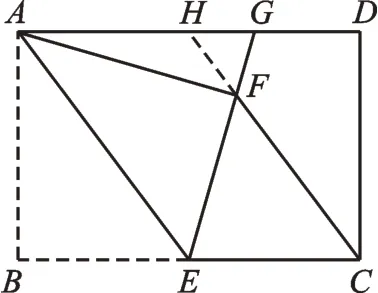
图7

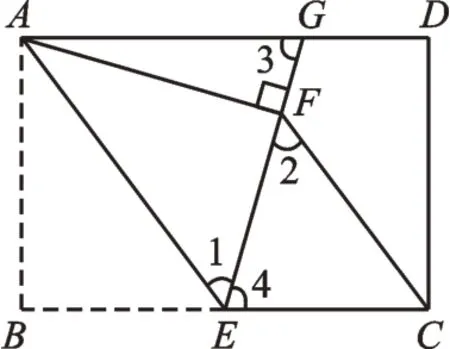
图8

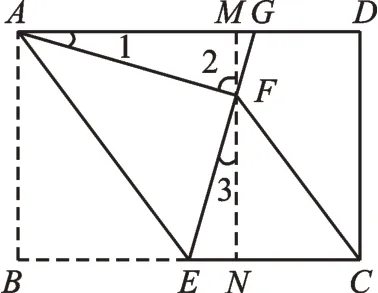
图9

方法6（三角形全等）：如图10，过点G作GH⊥BC于点H。易证四边形AGHB为矩形，则GH=AB=AF，∠AGH=∠AFG=90°。由AG//BH，得∠AGF=∠GEH，易证△AFG≌△GHE。设GF=x，则GE=3+x，EH=GF=x，GH=AB=4。在Rt△GEH中，EH2+GH2=EG2，则x2+42=（3+x）2，解得x=，则GF。

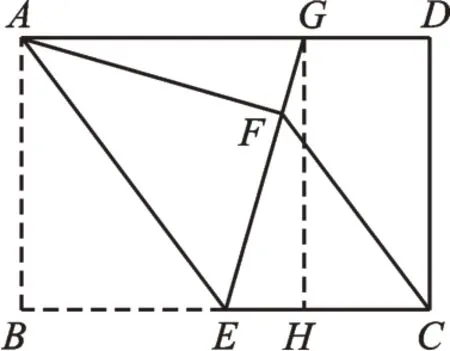
图10

方法1 与方法2 的突破口在“等腰三角形”，可通过平行线+角平分线产生的角度数量关系得到一组相等的角，进而得到“等腰三角形”。方法1 侧重等腰三角形的“腰相等”，通过设未知数，利用勾股定理列方程求解；方法2 侧重等腰三角形的对称性，利用“三线合一”的性质求出相应的线段，再利用“三角函数”求解线段。

方法3、方法4 利用相似进行求解。在方法3 中，已知EF，求GF，观察到AD//BC，进而通过延长线段，构造常见的“8 字型”相似求解；在方法4 中，发现图中不需要添加辅助线，便得到EF和GE所在的三角形相似（△AGE∽△CEF），进而得解。

方法5 与方法6 是利用解决以矩形为背景的问题中最常见的方法（化斜为直）来解决问题，其本质是通过作垂直构造直角三角形，利用直角三角形特殊的边角关系进行求解。

至此，虽一题多解，但通过多种方法的总结与内化，我们发现，万变不离其宗，多解可以归一，“平行+角平分线模型”“三角形相似”“化斜为直”是解决矩形翻折问题重要的突破口。