基于三角函数的改进混沌加密系统研究

薛建华,徐蔡余

(1.南京理工大学 泰州科技学院,江苏 泰州 225300;2.南京理工大学 公共事务学院,江苏 南京 210014)

随着技术不断革新,互联网带动着社会高速发展,但其无边界的特性,给信息安全带来了巨大的挑战。近些年,一种“以数据为中心”的安全理念被提出并广为讨论和研究,其中密码技术备受关注。利用非线性系统迭代结果难以预测、对初始条件的变化极端敏感、运行效率高、保真度高等特性而提出的混沌加密方法,是密码技术领域的一个新兴研究方向,应用前景十分广阔[1,2]。

混沌加密的关键基础是混沌非线性系统,例如传统的Logistic映射、Sine映射、PWLCM映射、Kent映射、Henon映射、Lorenz映射等[3-6]。近些年来,一些专家学者提出新的混沌加密系统,以应对日益复杂、严峻的信息安全形势,例如：周红亮等[7]提出一种新的混沌系统结合DNA编码的加密算法,实现了较高的加密、解密效率,但计算复杂,且受限于GTCA配对规则,易遭受攻击;汪乐乐等[8]针对传统的混沌系统安全性低的问题,提出一种基于Henon映射与Logistic映射的分数阶双混沌系统,实现了较强的初值敏感性和较低的计算复杂度,但混沌系统的叠加并不能扩大有效参数空间;王永等[9]通过对Sine映射进行分段处理和参数耦合,提出一种三维混沌模型,实现了更大的Lyapunov指数以及更均匀的概率分布;贾晓霞等[10]结合Tent映射提出一种高维混沌扩散的加密方案,扩大了密钥空间、增强了安全性能;Khade等[11]将Logistic映射拓展为三维系统3D-Logistic,Lone等[12]将3D-Logistic与Arnold变换、仿射希尔密码进行组合,通过图像加密进行了验证;Dua等[13]利用余弦函数对三维混沌系统ILM进行改进尝试,推导出新的三维混沌系统CT-ILM;张赛男等[14]通过联级耦合实现了logistic-sine-cosine混沌加密,获得了较好效果,进一步验证了三角函数在混沌加密方面的优势。

相比而言,传统的一维混沌系统结构形式简单、运行效率高、易于实现,但处于混沌状态的参数空间较窄,有效密钥空间有限,安全性不高。新兴混沌系统及相关加密算法,往往结构复杂、实现难大度,要么相空间分布不均匀或呈现规律明显易遭受攻击,要么运行效率低下、实用性不强,呈现出一定的局限。研究新的具备较大参数范围、较好混沌效果、运行效率高、形式简单的多维非线性系统,是十分实际而又有意义的工作,也是当下的一个热点[15]。

本文通过对一个基于正余弦的二维混沌系统进行优化改进,进一步拓展出新的三维混沌系统;根据Lyapunov指数、分岔图、相位图以及混沌时序图、直方图等,来反映系统改进后的混沌性能;采用编码加密算法进行仿真试验,通过对系统改进前后的试验结果分析、对比,验证该方法的可行性和适用性。

1 改进的三维混沌系统

刘明明等[16]提出一个基于正余弦的二维混沌系统(详见式1),结构简单、运行效率高,但在加密应用时存在一些不足：一是有效参数空间不连续且阶段性有效范围较窄(如图1(a)所示),随着参数值增大,系统不断出现向稳定态收敛的现象,应用价值受限;二是相空间分布不均匀,呈现规律较明显(如图1(b)所示),并且混沌直方图两端高、中间低(如图1(c)、(d)所示),分布不均匀,易遭受攻击。出现这些不足,主要原因是式(1)设计简单且正余弦函数的弧度值子公式相近,当Xn=π/4-k·π或Yn=k·π-π/4(k∈Z)时正余弦值相等,易造成2个子式等效。文献[16]通过参数与正余弦函数相乘扩大了相空间范围,但也增大了子式等效的概率。

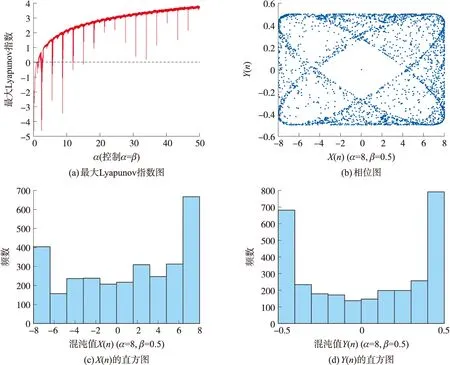
图1 式(1)的最大Lyapunov指数图、混沌相位图及直方图

(1)

1.1 改进思路

(1)本文针对上述不足,首先从两个方面进行改进：一是舍弃与正余弦函数相乘的参数,将迭代变量的值范围控制在[-1,1],虽然缩小了相空间范围,但也降低了系统向稳定态收敛的概率;二是改造正余弦函数的弧度值子公式,分别对其中一个变量添加控制参数与其相乘,提高结构复杂度,避免失效。

改进后的二维混沌系统函数关系公式如下

(2)

(2)令f1的控制参数ρ等价于常量-λ,公式变换如下

f1(Xn,Yn)=cos(Xn-λYn)=cos(λYn-Xn)

(3)

构造出新的二维混沌系统

(4)

(3)引入新变量Z,令

Zn+1=f3(Xn,Yn)=tan(γXn·Yn)

(5)

式中：(γXn·Yn-π/2)(modπ)≠ 0,由于Xn∈[-1,1]、Yn∈[-1,1],故本文取γ=1.19。

(4)用变量Z分别代换f1与f2的变量X和Y,提高系统复杂度

Xn+1=f1(Yn,Zn)=cos(λYn-Zn)

(6)

Yn+1=f2(Xn,Zn)=sin(μXn-Zn)

(7)

(5)对系统添加控制参数α、β,令α与其相乘扩大相空间范围,对β取模将相空间映射到值域[0,β),让混沌分布更加均匀。函数关系变换如下

(8)

经上述改进,拓展出一个新的三维混沌系统,命名为“CST-3D”,其函数关系公式为

(9)

式中：α≥β≥1。为了实现较均匀的混沌分布,本文取α=10 000、β=10。

1.2 混沌性能

CST-3D的Jacobian矩阵式为

(10)

控制参数λ=μ,通过Matlab仿真计算Jacobian矩阵得出Lyapunov指数[17],如图2中(a)图所示：μ∈[0,+∞)时,Lyapunov指数恒大于0,系统保持着稳定且连续的混沌状态,并与图2中的分岔图(b)、(c)和(d)形成对应,效果较好。

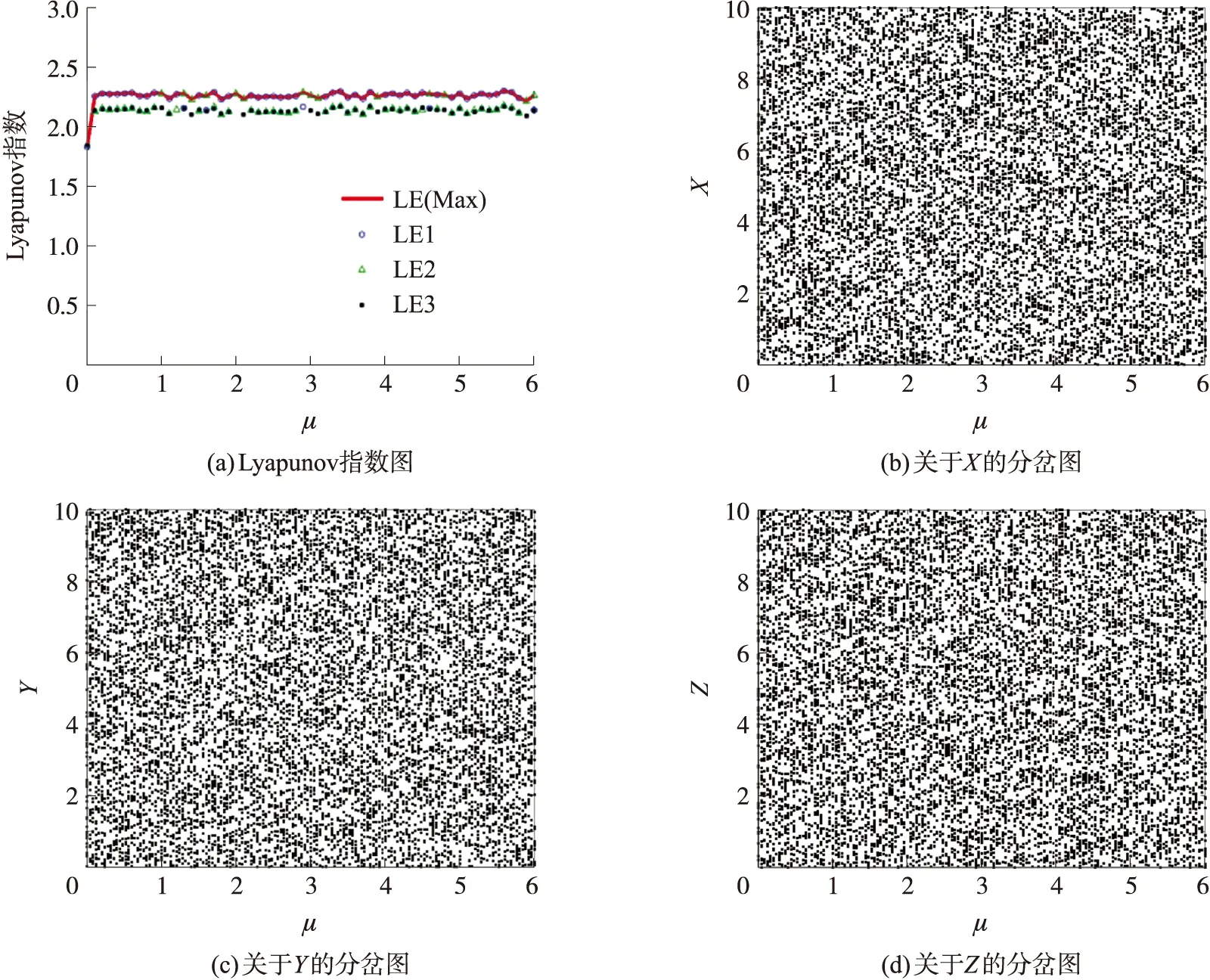
图2 CST-3D的Lyapunov指数图和分岔图

令g(X,Y,Z)=0,计算出系统仅有1个平衡点s=(0,0,0)。对该平衡点线性化得Jacobian矩阵J0为

(11)

其特征值λ0=0,可见平衡点s为不动点。系统CST-3D要进入混沌状态,其初始值(X0,Y0,Z0)≠(0,0,0)。

取CST-3D的参数λ=5.6、μ=4.8,变量X、Y、Z的初始值为(1,1,1),迭代运算后的结果如图3和图4所示。由图可见,X、Y、Z的值混乱无序,直方图分布均匀,混沌吸引子呈现出良好的混沌效果。

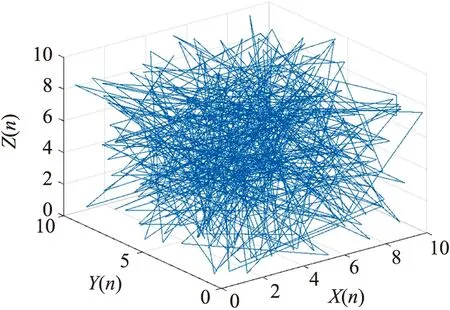
图3 CST-3D的混沌吸引子

图4 CST-3D的混沌时序图及直方图

1.3 对比分析

对比来自文献[16]的式(1),新系统CST-3D在三个方面有明显改进：

(1)对比图1(a)与图2(a)可知,CST-3D解决了式(1)有效参数空间不连续且随着参数增大不断向稳定态收敛的局限。CST-3D在参数μ∈[0,+∞)时便可进入连续、稳定的混沌状态,有效参数空间更大,实用性更佳。

(2)对比图1(b)与图3可知,CST-3D解决了式(1)的相空间分布区域遍历性差的问题。式(1)的相空间存在固化的边界,其X∈[-8,8]且Y∈[-0.5,0.5],范围受限且分布规律明显;而CST-3D的相空间范围为(X,Y,Z)∈[0,β),大小取决于控制参数β,范围更大、更可控且分布遍历性较好。

(3)对比图1(c)、(d)与图4(d)、(e)、(f)可知,CST-3D解决了式(1)中混沌直方图“两端高、中间低”的分布不均匀问题,且受控于参数α与β的差值,加密应用中安全性能更高。

2 试验验证

混沌加密属流密码范畴,是利用混沌非线性系统生成密钥序列与明文进行耦合的一种加密方法。为验证上述混沌系统的可行性,本文采用编码加密算法进行仿真试验,并重点围绕安全性进行分析和对比。

2.1 编码加密算法

编码加密算法的大致思路是：将混沌系统的初值(X0,Y0,Z0)以及初始迭代次数M作为密钥,用混沌系统进行迭代运算产生一系列混沌值并组成流密码序列,然后扩散至GF(216)。其中,密钥序列的生成原理如下。

步骤1CST-3D迭代运算生成一系列混沌值。函数关系公式如下

(12)

(13)

式中：1≤i≤n-1。

步骤2每个混沌值取t个有效数,按一定逻辑形成混沌序列T,相应函数关系公式如下

(14)

式中：1≤k≤n,0≤i≤t-1。

步骤3依次局部选取混沌序列T的5位密钥集,形成流密码序列K,并逐一对216取模,将每一位密码均扩散至GF(216)。函数关系公式如下

Ki={Ti,T(i+1)(modp),T(i+2)(modp),T(i+3)(modp),

T(i+4)(modp)}(mod216)

(15)

K={K0,K1,…,Kp-1}

(16)

式中：0≤i≤p-1,p=3nt。

上述过程中,流密码序列K的长度p不小于明文长度;其密钥空间为216p,随着密码长度的增长呈指数式扩大,可有效抵御穷举攻击。混沌迭代次数d≥1,具体取值可根据实际应用场景综合运行效率确定。密钥扩散的思路,依据混沌自相似性理论,即局部选取的混沌密钥集在分布形态上与整体相似[18,19],保持着混沌序列整体的伪随机特征。如此,既能获得较好的加密效果,又能实现较快的加密、解密速度。

2.2 混沌密钥序列随机特性测试

本文依据国家标准《信息安全技术 二元序列随机性检测方法》,对混沌加密系统产生的密钥序列进行了随机性测试。分别以本文CST-3D、文献[16]的式(1)、文献[11]的3D-Logistic、文献[13]的CT-ILM等4个混沌系统为基础,用编码加密算法生成1MB的混沌密钥序列作为实验对比样本,测试结果如表1所示。

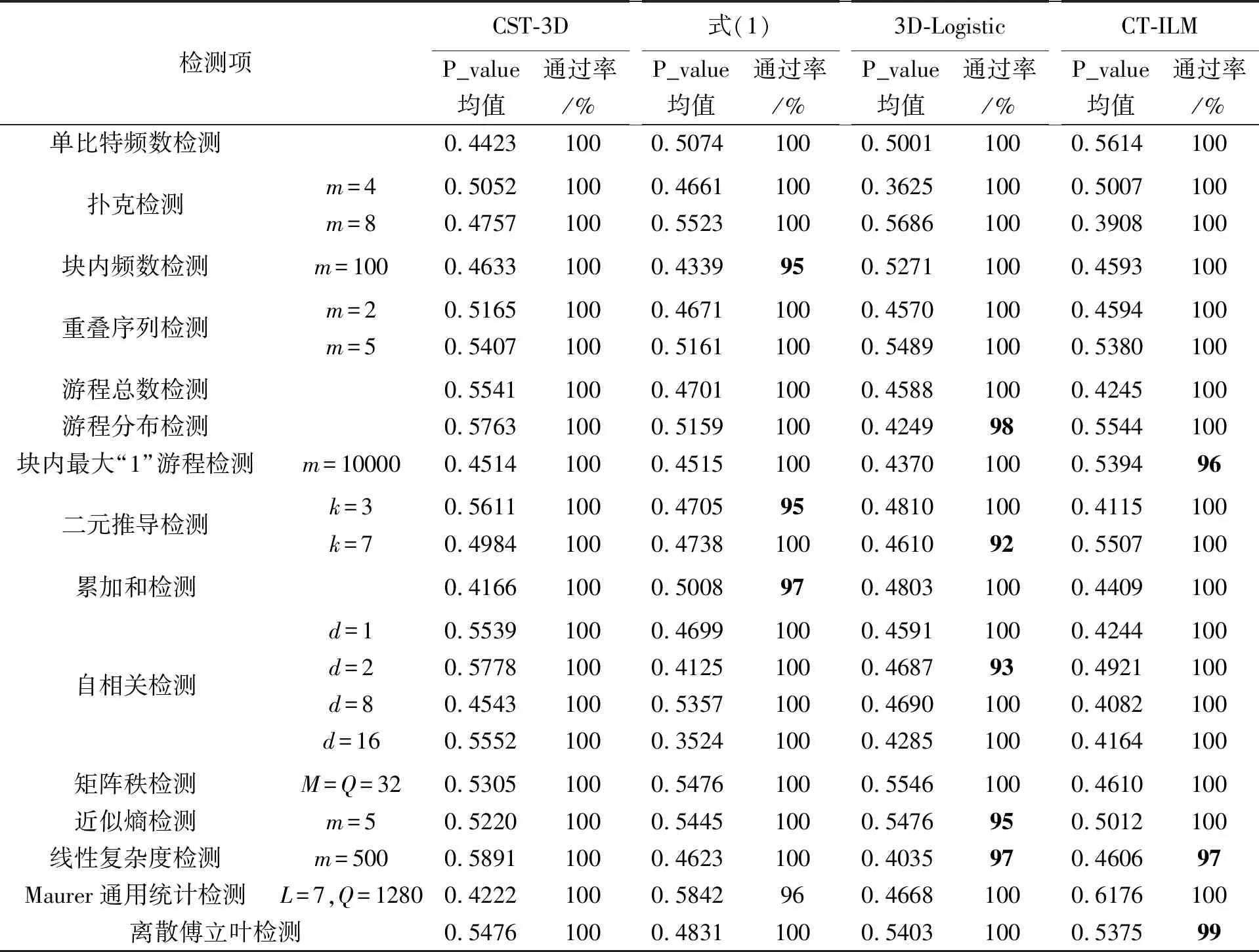
表1 混沌密钥序列随机特性检测结果及对比

CST-3D生成的混沌序列样本,15项检测全部100%通过,测试结果P_value均大于显著性水平α(α=0.01);式(1)生成的样本,在块内频数检测、二元推导检测(k=3)、累加和检测、Maurer通用统计检测等4项试验中,存在小概率检测不通过情况;3D-Logistic生成的样本,在游程分布检测、二元推导检测(k=7)、自相关检测(d=2)、近似熵检测、线性复杂度检测等5项试验中,检测没有完全通过,个别项目不通过机率接近8%;CT-ILM生成的样本,在块内最大“1”游程检测、线性复杂度检测、离散傅立叶检测等3项试验中,小概率检测不通过。由此可见,本文的三维混沌系统CST-3D与编码加密算法符合国家随机性检测标准;对比国内外相关研究发现,混沌系统的随机性能CST-3D>CT-ILM>式(1)>3D-Logistic。

2.3 流密码序列信息熵与初始条件敏感性测试

本文基于CST-3D系统的编码加密算法,生成的流密码序列信息熵较大,呈现出较高的不确定性,如图5所示。尤其当数据量不超过16 KB时,流密码序列的信息熵近似于理论极值。可见,该方法具有良好的抗熵值分析攻击性能。

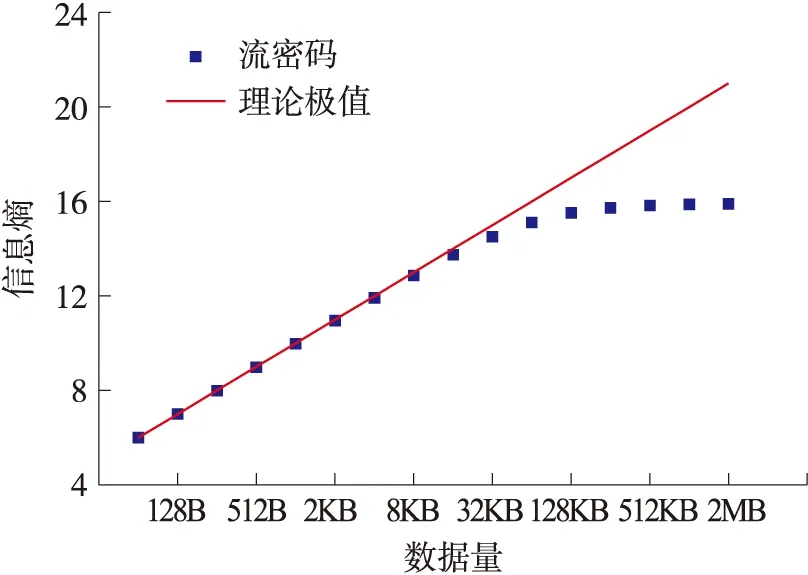
图5 流密码序列信息熵分析

与传统动力学系统不同的是,混沌系统微小的初始差异将随着时间不断放大,迭代运算产生的混沌序列甚至有可能完全不同。根据范九伦等[20]提出的初值敏感性检验方法,设定CST-3D系统初值(X0,Y0,Z0)=(1,1,1)、参数(λ,μ,γ)=(5.6,4.8,1.19)、初始迭代次数M=300,通过对上述7个值逐一进行微小变化后生成1MB流密码序列,用编辑距离算法分别计算相似度,进行两两对比分析差异,结果如表2所示。初值或参数微小变化前后生成的流密码序列,差别很大;8种实验条件下产生的流密码序列,彼此之间相似度小于0.008%,几乎完全互不相同。可见,本文提出的混沌系统CST-3D对初始条件极为敏感,具备良好的抗差分分析攻击性能。

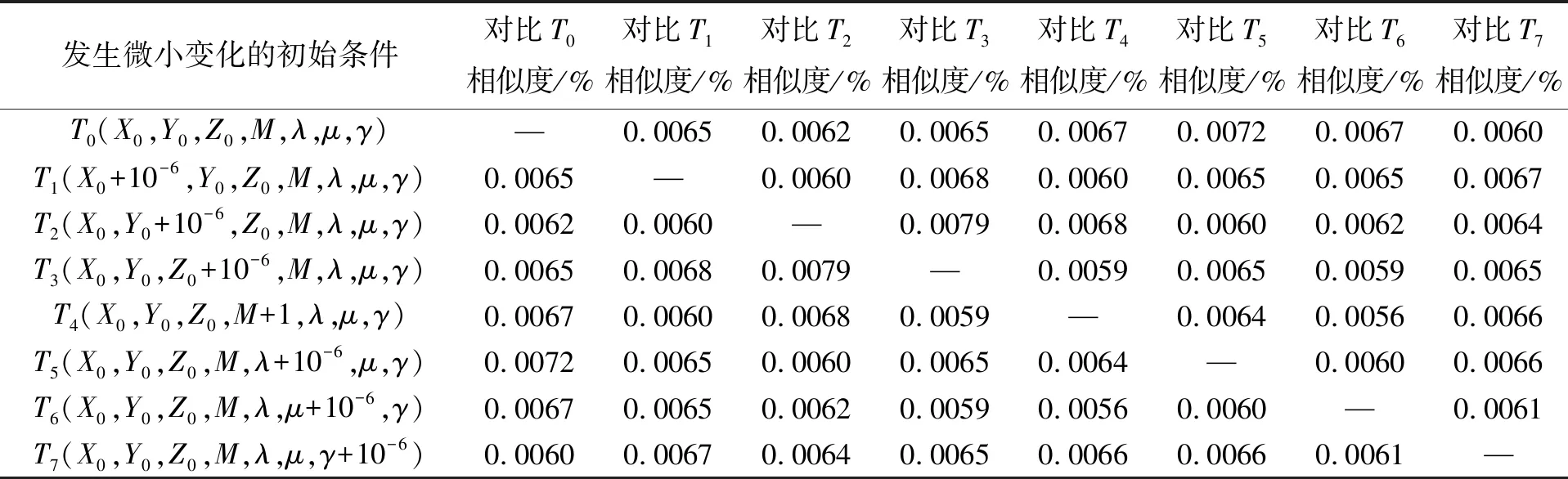
表2 初始条件微小变化前后生成的流密码序列相似度检测结果

2.4 明文与密文直方图对比

学生档案中的《普通高等学校招生考生报名登记表》,加密前后的直方图如图6所示。加密前,明文的直方图分布特征十分明显;加密后,直方图分布均匀,明文统计特征完全被隐藏。对比发现,CST-3D系统加密产生的密文直方图,较“式(1)”与3D-Logistic的密文直方图分布更加均匀,没有特别明显的统计特征,可以较好地抵御统计攻击;与国外学者新提出的CT-ILM系统相比,效果不相上下。

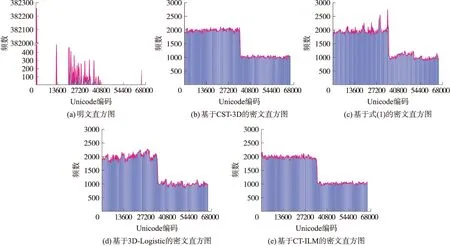
图6 学生《普通高等学校招生考生报名登记表》直方图及对比

3 结束语

本文通过对一个二维正余弦混沌系统进行改进、优化,并进一步拓展出新的三维混沌系统CST-3D,采用编码加密算法进行了仿真试验验证。结果表明,本文方法具有以下特性和优势。

(1)CST-3D系统混沌性能良好,当参数λ=μ≥0便可进入连续、稳定的混沌状态,有效参数空间得到进一步扩大。迭代运算后,变量X、Y、Z的值混乱无序,直方图分布均匀;相空间遍历性佳,范围拓展至[0,β),空间更大、更可控。

(2)CST-3D系统和编码加密算法,符合国家随机性检测标准,对初值和参数的变化极为敏感,生成的流密码序列信息熵较高,安全性较好。信息加密后直方图分布均匀,明文统计特征完全被隐藏,具有良好的抵御攻击能力。

(3)CST-3D系统形式简单、运行效率高,实际应用价值颇高。系统设定了5个控制参数,给加密应用的安全设计提供了更多的空间,在政务平台、金融网络、教育招生等对信息安全要求较高的领域更具优势,应用前景广阔。