污染环境下具有强Allee 效应的食饵-捕食系统收获策略 *

钟 颖，韦煜明，彭华勤

（广西师范大学 数学与统计学院，广西 桂林 541006）

0 引言

据2020 年合国的报道，过去40 年生物多样性降低了68%，最主要的原因是人为活动，例如过度开采，环境的污染和气候的变化等，因此对渔业资源进行科学的管理［1-4］是很有必要的。由于工业迅速发展，工业废水排放量增加，导致水生环境的污染更加严重，美国杂志《科学》报道，如果不缓解海洋污染和过度开采，到2050 年之前，渔业资源的物种和数量将趋于灭绝。因此建立具有毒素污染和收获的食饵捕食的数学模型具有重要的现实意义。Kar［5］与Das［6］研究了在有毒环境中，具有捕获的食饵-捕食模型，Kar［7］讨论了两类竞争种群在污染环境中的收获策略。当种群密度降低时，种群动力学的经典观点认为，由于自然资源有限，个体在较低的数量下会有更好的发展，但Allee 效应认为情况正好相反，对于濒危的物种更容易受到Allee 效应的影响，增加灭绝的可能性。因此具有Allee 效应的研究受到了重视。［8-12］

我们改进文献［6］中的食饵捕食模型，假设猎物受到强Allee 效应的影响，Das 忽略了消化饱和因素，在本文中加入Holling-Ⅱ型饱和功能反应函数在对种群资源进行捕获时，文献［6］没有考虑到现实生活中对物种需求的差异性，本文设猎物和捕食者的捕捞努力量分别为E1、E2。基于以上假设，我们构建数学模型：

其中x(t)，y(t) 分别代表猎物和捕食者在t时刻的种群密度，猎物种群按logistic 增长率生长，r1、k1分别是猎物种群的自然增长率和承载能力，种群密度必须超过m才能存活，d为捕食者死亡率，q1、q2分别是猎物和捕食者的捕获系数，α表示捕食者对猎物种群的消耗率，β为转化率，γ1x3、γ2y2分别表示外界毒素对猎物和捕食者种群的影响，其中猎物直接受到外界毒素的感染，捕食者以猎物为食受到间接感染。

接下来讨论该模型的局部稳定性，全局稳定性及最优收获策略。利用理论分析，可以实现更科学的可持续资源利用以及良好的经济效益，从而促进渔业的发展。

1 平衡点的稳定性分析

灭绝平衡点A0对于所有参数值都存在；当捕食者消失即y= 0 时，通过计算得到，其中故时，边界平衡点存在；联立方程（2）（3）消除yˉ，有

当M3＜0，M4＜0 时方程（5）存在唯一的正解［13］。由式（2），当时，

此时，正平衡点A3(xˉ，yˉ) 存在。

定理1（i）对于所有参数值，A0总是渐近稳定的；

（iv）当ω1＞0，ω2＞0 时，A3是稳定结点或稳定焦点。

证明：给出系统在任意平衡点(xe，ye) 的Jacobian 矩阵

（i）对于A0，其特征方程是( -mr1-q1E1-λ)( -d-q2E2-λ)= 0，特征方程根λ1=-mr1-q1E1＜0，λ2=-d-q2E2＜0，因此A0是局部渐进稳定的。

（ii）对于A1，其特征方程是：

因此当λ1＜0，λ2＜0 时，A1是局部渐进稳定结点。

（iii）对于A2，其特征方程是：

如果λ1＜0，λ2＜0 被满足时，A2是局部渐进稳定结点。

（iv）对于A3，它的特征方程是

其中

当毒素不存在时，即γ1=γ2= 0，此时因此当ω1＞0 时，λ1，λ2是2 个负实数或带有负实部的共轭负根，此时A3是一个稳定的结点或焦点。可以得出结论，在满足条件时，共存平衡点在有毒素和无毒素情况下的稳定性不改变。

2 全局稳定性

在这一节，通过构建合适的Liapunov 函数研究模型（2）的全局稳定性。定义Liapunov 函数：

其中h，j是待定的正常数，容易证明得，在非平凡平衡点(xˉ，yˉ) 处有V= 0，除了(xˉ，yˉ) 以外的正常数(x，y) 都有V＞0。

定理2条件满足时，正平衡点A2是全局渐近稳定的。

证明：式（7）对t求导，有

3 生物经济平衡

Clark［14］指出生物平衡是由ẋ=ẏ= 0 给出的，生物经济平衡［16］是生物平衡和经济平衡的组合，经济平衡由π= 0 给出。令c1，c2分别是猎物和捕食者每单位捕捞努力量的成本，p1，p2分别是猎物和捕食者每单位生物量的价格，假定都是常数，则净收入函数：

下面分3 种情形讨论：

情形1：c1＞p1q1x，此时捕捞猎物的成本大于利益，因此停止捕捞，即= 0。从方程（9c）中有

将式（10）代入到（9a）中，得

(H1)其中x*是方程（11）的正根，当(H1) 成立时，情形1 的生物经济平衡存在。

情形2：c2＞p2q2y，此时捕捞捕食者的成本大于利益，因此停止捕捞，即= 0。从方程（9c）中有

将式（12）代入到（9b）中，得

(H2)：当(H2) 成立时，情形2 的生物经济平衡存在。

情形3：c1≤p1q1x，c2≤p2q2y，此时捕捞猎物和捕食者的利润大于等于成本，故两种物种都捕捞。由式（9c），有

把（14）代入到（9a）（9b）中，得

当(H3) 和(H4) 同时成立时，情形3 的生物经济平衡存在。

4 最优收获策略

在本节中，用Pontryagin′s 最大值原理［16］探讨最优收获策略，目标是使受状态方程（1）约束的J最大化，考虑连续收入时间流的现值J：

其中δ是瞬时年贴现率，π(x，y，E1，E2)=(p1q1x-c1)E1+(p2q2y-c2)E2，控制变量Ei(t) 受到

的约束，这里的Emax是收获努力量的最大可行上限。

构造哈密顿函数［14］：

其中λ1(t)，λ2(t) 是伴随变量，令σ1(t)=e-δt(p1q1x-c1)-λ1q1x，σ2(t)=e-δt(p2q2y-c2)-λ2q2y为开关函数，由于哈密顿函数是伴随变量的线性函数，因此最优控制必须是Bang-Bang 控制和奇异控制的结合。

在Bang-Bang 控制中，最优收获策略的Ei(t) 必须满足以下条件：

函数λi(t)eδt，i=(1，2) 为影子价格，p1q1x-c1为收获猎物的利益，p2q2y-c2为收获捕食者的利益，因此当成本小于经济利润时，E(t)=Emax，当成本大于经济利润时，E(t)= 0。

当σ(t)= 0 时，最优控制E*：0 ＜E*＜Emax。此时控制约束没有控制力，有，可得

在文献［13］中，伴随变量λ1(t)，λ2(t) 满足以下式子：

我们考虑上述问题的最优平衡解，由ẋ=ẏ= 0 解得

把式（22）和（23）分别代入到式（20）和（21）中，整理可得

从方程（24）和（25）中消除λ2，引入微分算子，得到

其中

数或具有正实部的共轭复数，此时方程（26）的解的形式是：

其中A1，A2是任意常数

如果A1=A2= 0，则λ1有界，

同理可得

其中B1，B2是任意常数

如果B1=B2= 0，则λ2有界

联立方程（22）（23）和（30）可以得到最优平衡解。

再次写出经济利润的表达式：

注意到：（i）当δ→∞时，此时经济利润消失；

（ii）当δ→0 时，经济利润达到最大值。

5 数值模拟和结论

在本小节中，通过数值模拟验证上面的分析结果。将参数值分别设置为r1= 0.6，k1= 40，m= 0.02，α= 0.5，β= 0.3，b= 0.8，d= 0.01，γ1= 0.005，γ2= 0.008，q1= 0.04，q2= 0.01，E1= 2，E2= 4。

例1：模型（1）的灭绝平衡点A0对于所有参数总是稳定的，通过计算可以得到系统的边界平衡点A1=(29.8609，0)，A2=(0.154，0)，系统的共存平衡点A3=(0.1943，0.0551)；其中A1的两个特征值λ1=-17.7415，λ2= 0.3099，因此A1为鞍结点；A2的两个特征值λ1= 0.0915，λ2=-0.0089，因此A2为鞍结点；对于共存平衡点，通过计算求出ω1=-0.1179，ω2= 0.0009，因此可以得到λ1+λ2=-ω1＞0，λ1λ2=ω2＞0，它的两个特征值具有正实部，故A3不稳定。利用软件Matlab 画出系统在各类平衡点处的相位图，从图1 中可以得到：结论与上述分析的结论相一致。

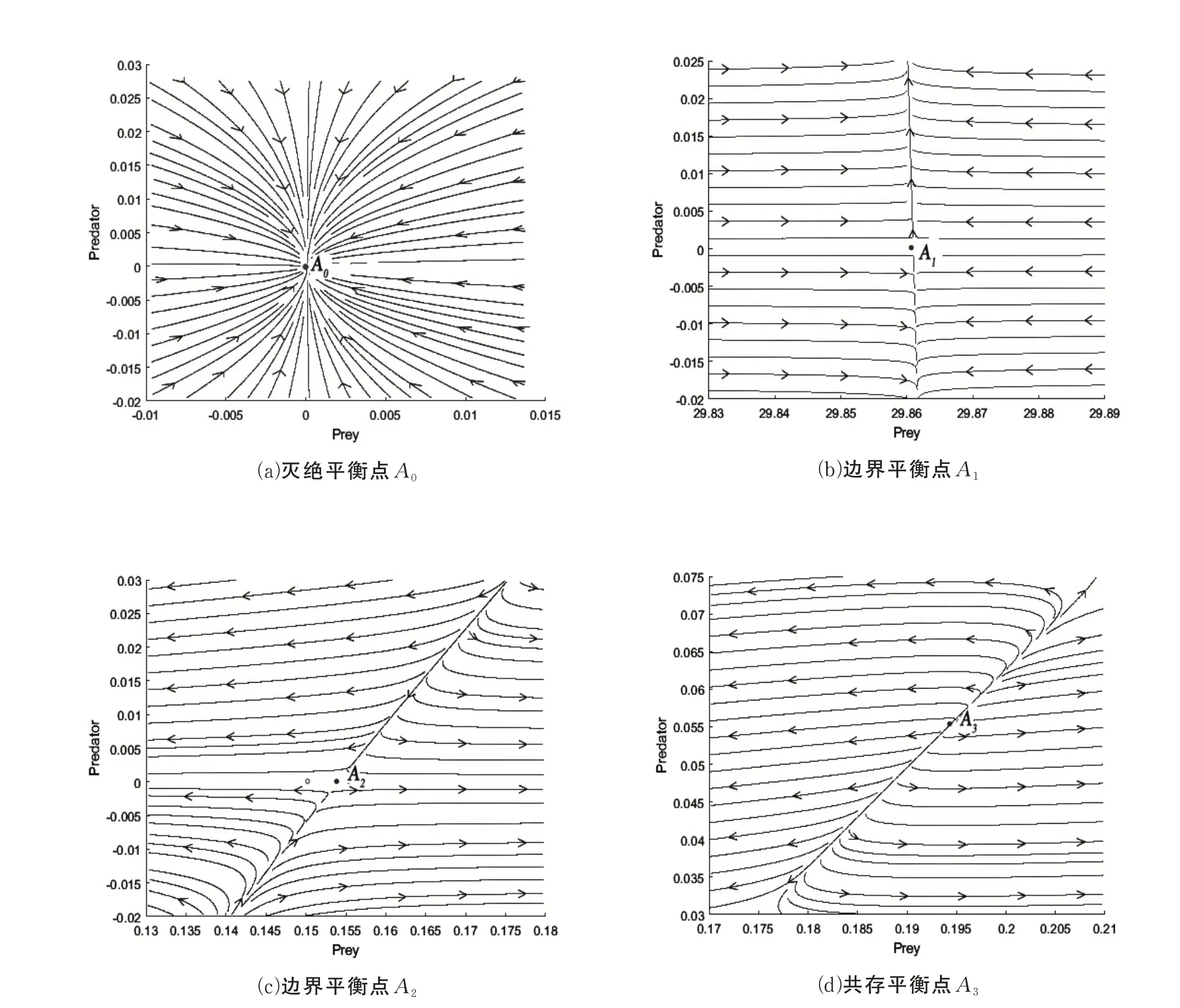
图1 系统在不同平衡点的相位图

当外界毒素不存在即γ1=γ2= 0 时，计算得到共存平衡点A3=(0.1923，0.0528)，ω1=-0.6109 ＜0，此时共存平衡点仍保持不稳定。

例2：设参数值q1= 0.4，α= 0.05，p1= 0.5，p2= 0.6，c1= 3，c2= 2，γ2= 0.0002，其他参数与例1 一样保持不变，

上述结果表明，外界毒素不存在时情形2 的生物经济平衡点不存在，但情形1 和3 的生物经济平衡点存在，因此毒素并不影响生物经济平衡点的存在性，但是在没有外界毒素存在时，观察到情形1 生物经济平衡点处的猎物种群密度比在有毒素存在条件下的种群密度要高，情形1 和情形3 在生物经济平衡点的捕捞努力量也比在有毒素情形下的要高。这说明了毒物系数强度影响系统的生物经济平衡点的大小，但不会影响其存在性。

例3：设置参数，其余参数与例1 相同，利用软件Matlab 分别画出猎物和捕食者种群在有毒素和没有毒素情形下的时间序列图，分析毒素存在对种群大小的影响。

从图2 中可以看到猎物种群在不同毒物浓度下都趋于一个确定的常数，但毒素存在时的猎物种群密度低于毒素不存在的情形。由图2，可以看到毒素存在时捕食者种群随着时间趋于一个确定的数，而当毒素不存在时，捕食者种群会一直增加。因此能够得出结论：随着毒性作用的增加，这两个物种的种群密度将逐渐下降，当毒物系数足够大时，种群最终将有灭绝的趋势。

图2(a) 猎物和捕食者种群在污染环境下的时间序列图

图2(b) 猎物和捕食者种群在环境无污染下的时间序列图

表1 污染环境下的生物经济平衡点

表2 无污染环境下的生物经济平衡点