不确定平方和凸多项式优化的SDP松弛与鲁棒鞍点刻画

谭 玟,孙祥凯

(重庆工商大学 数学与统计学院,重庆 400067)

凸多项式优化是凸优化问题的一个重要模型,在自动控制系统、交通运输和工程设计等领域应用广泛,并取得了很多研究成果[1-4].平方和凸多项式优化作为凸多项式优化问题的一个子类,近年来也得到广泛关注,因为它可以等价地表示为一个半定线性优化问题,并能通过内点法有效解决[5].此外,平方和凸多项式优化具有精确的半正定规划(SDP)松弛问题,且原问题与其对偶问题之间存在零对偶间隙[6-8].

上述研究平方和凸多项式优化问题时,通常需要假设所考虑优化问题模型的数据是精确的.但在实际应用中,由于测量、制作误差以及不精确数据等诸多因素影响,所建模型的优化问题不可避免地存在不确定数据.因此,带有不确定参数的平方和凸多项式优化问题目前已引起人们广泛关注.例如: Jeyakumar等[9]基于常见的不确定集,得到了不确定平方和凸优化问题的鲁棒解刻画和精确的SDP松弛问题; Chuong[10]借助线性矩阵不等式以及平方和条件,研究了不确定多目标平方和凸多项式优化问题的最优性条件和对偶定理; Jiao等[11]借助标量化方法,刻画了不确定多目标平方和凸多项式优化问题的鲁棒有效解,并证明了对应的标量问题与松弛问题之间的零对偶间隙; Chuong等[12]借助一类鲁棒型闭凸锥约束规格,刻画了不确定凸二次多目标优化问题的鲁棒(弱)有效解的最优性条件.

受上述研究结果的启发,本文给出一类不确定平方和凸优化问题的鲁棒鞍点定理.首先,借助鲁棒优化方法,引入不确定平方和凸多项式优化问题的鲁棒对等问题; 然后,借助一类鲁棒型特征锥约束规格,得到该不确定平方和凸多项式优化问题的精确SDP松弛问题; 最后,引入该不确定平方和凸多项式优化问题的Langrange函数,并借助平方和条件给出其鲁棒鞍点定理.

1 预备知识

定义1[5]设f为n上的实多项式,若多项式

f(x)-f(y)-f(y)T(x-y)

注1显然,平方和凸多项式是凸多项式,但反之不一定成立[13-14].进一步,凸二次函数和凸可分离多项式都是平方和凸多项式.此外,一个平方和凸多项式可能既不是二次的也不是可分离的[5].

本文考虑如下不确定平方和凸多项式优化问题(UP):

其中vj(j=1,2,…,m)为不确定参数且属于不确定集Vj⊆k,f:n→和gf:n×Vj→(j=1,2,…,m)均为给定的函数.若无特殊说明,本文总假设f是平方和凸多项式,对任意的vj∈Vj,gj(·,vj)是平方和凸多项式,对任意的x∈n,gj(x,·)是仿射函数,即

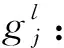
定义2问题(UP)的鲁棒可行集定义为

F∶={x∈n|gj(x,vj)≤0,∀vj∈Vj,j=1,2,…,m}.

2 精确SDP松弛

下面借助一类鲁棒型约束规格,建立问题(UP)的精确SDP松弛问题.

2) 显然,若鲁棒Slater条件

{x∈n|gj(x,vj)<0,∀vj∈Vj,j=1,2,…,m}≠Ø

成立,则鲁棒型特征锥约束规格(RCCCQ)成立[19].因此条件(RCCCQ)弱于鲁棒Slater条件.

下面借助条件(RCCCQ),给出问题(UP)的精确SDP松弛问题.

定理1对于问题(UP),假设F≠Ø.若条件(RCCCQ)成立,则

证明: 结合文献[20]中定理3.1及文献[21]中定理2.1的证明方法,易得结论成立.

推论1[9]对于问题(UP),假设F≠Ø.若鲁棒Slater条件成立,则

证明: 由注2中2)并结合定理1,易得结论成立.

注3由于条件(RCCCQ)弱于鲁棒Slater条件,因此定理1改进并推广了文献[9]中定理2.3的相关结果.

若不确定集Vj(j=1,2,…,m)为单点集,则易得如下结论.

推论2考虑如下平方和凸多项式优化问题(P):

假设{x∈n|gj(x)≤0,j=1,2,…,m}≠Ø,且f:n→与gj:n→(j=1,2,…,m)均为平方和凸多项式.若条件(CCCQ)成立,则

3 鲁棒鞍点定理

注4若不确定集Vj(j=1,2,…,m)为单点集,则问题(P)的Lagrange函数定义为

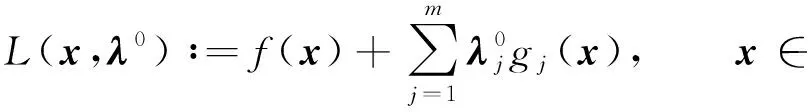
即对任意的x∈n,有

(1)

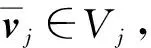
故结合式(1)可得

另一方面,对任意的x∈n,有

例1设m=1,k=2.令不确定集V1⊆2为

考虑不确定平方和凸多项式优化问题(UP):

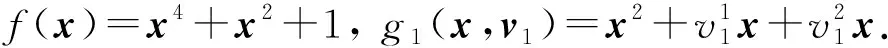
易证

证明: 由注2中2)并结合定理2,易得结论成立.

证明: 由注2中1)并结合推论2及定理2,易得结论成立.