一维函数光子晶体的界面态

韩 梦,李 宏,张斯淇,赵东旭,刘晓静,吴向尧

(1.吉林师范大学 物理学院,吉林 四平 136000; 2.吉林工程技术师范学院 量子信息技术交叉学科研究院,吉林省量子信息技术工程实验室,长春 130052)

光子晶体是一种折射率周期变化的人工微结构材料[1-3],光子晶体应用广泛,其带隙和折射率等可根据需要进行调控,从而实现光的传输、控制和放大等,如基于光子禁带中禁止光传播的特性制备反射镜,通过控制光子禁带的范围,即可控制反射的频率范围.由于光子晶体具有光子带隙和光子局域特性,使其可精确控制光子运动,因此光子晶体将成为光电集成和光子集成的一种关键性基础材料[4].随着拓扑物理学的发展[5-6],界面态已成为光子晶体领域中的一个研究热点[7-8].文献[9-10]研究了光子晶体界面态,并给出2个反转对称光子晶体结构(PC)组合产生界面态的条件; 文献[11-12] 利用电子束蒸镀技术制备了具有反转对称特征的光子结构,通过实验证明了界面态的存在.一维光子结构的界面态类似带隙中的透射模,在一维反转对称结构构成的组合结构中,其界面态受拓扑特征保护,即对各类噪声具有很强的鲁棒性[13].文献[14]研究了具有反转对称特征的一维层状光子晶体结构,对光子晶体组合结构的阻抗虚部进行了计算,分析了组合结构中存在多个界面态的条件以及多界面态的位置和数目,并对组合结构内的电场分布进行了计算,结果表明,在界面态频率处的光波存在明显的光子局域.通过改变元胞数目可调控界面态的位置,并满足对界面态不同的应用需求.但上述研究的光子晶体均为常规型,即折射率为常数.本文利用传输矩阵法给出一维组合函数型光子晶体的匹配矩阵和传输矩阵,在此基础上研究一维函数光子晶体的界面态,并研究折射率端点值、介质厚度和入射角对界面态位置的影响,从而实现对界面态位置的调节.

1 一维函数光子晶体的匹配矩阵和传输矩阵

传输矩阵法是分析计算一维光子结构常用的方法,利用匹配矩阵和传输矩阵可逐层描述光波在层状光子结构的界面处以及在介质中的传输规律.光波在入射角为θj、厚度为dj的第j层常规介质中传输的传输矩阵P(kj,dj)[14]为

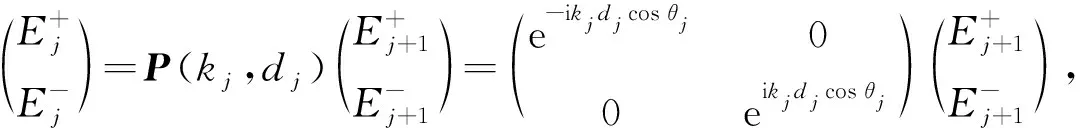
(1)

其中

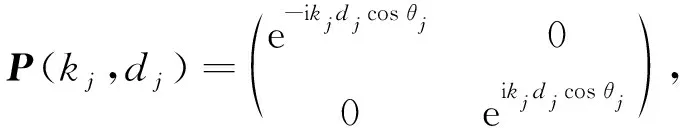
(2)

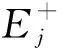
对于函数介质B,其折射率为线性函数型

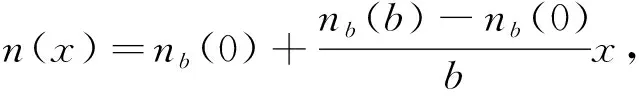
(3)

在光子晶体函数介质B中选取微元Δx,其对应的相位为

(4)

则厚度为b的函数介质B的相位为

(5)

将式(5)代入式(2)中,可得函数型介质B的传输矩阵

(6)

光波从第j层到第(j+1)层的电场强度关系[14]为

(7)

其中匹配矩阵

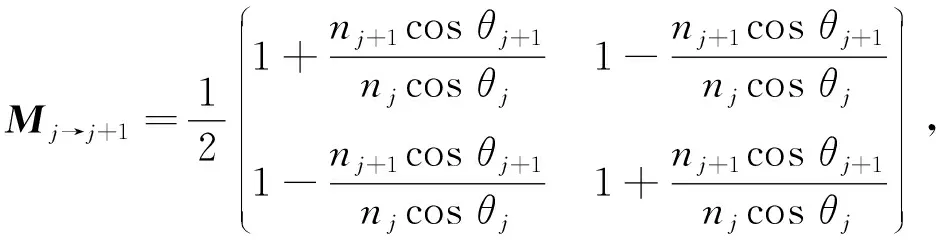
(8)

nj和nj+1分别为第j层和第(j+1)层介质折射率,函数型介质匹配矩阵在形式上与常规型介质匹配矩阵相同,但nj和nj+1对应函数型介质折射率的端点值.

光波在PCⅠ和PCⅡ结构中一个周期的传输矩阵TPCⅠ和TPCⅡ分别为

TPCⅠ=Pa·Mab·Pb·Mba·Pa,

(9)

TPCⅡ=Pb·Mba·Pa·Mab·Pb.

(10)

对于具有N个周期单元的一维反转对称光子结构PCⅠ+PCⅡ,当处在空气中时,入射光波从空气射入该结构后,在光子结构中传输后射入空气,此时总传输矩阵为

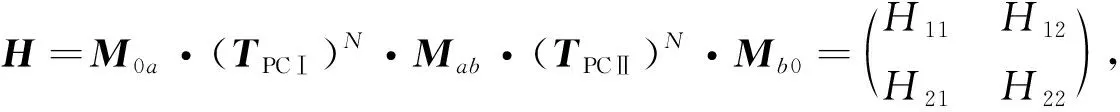
(11)

通过计算可得

(12)

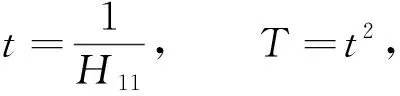
(13)

其中r为反射系数,t为透射系数,R和T分别为反射率和透射率.

光学结构的表面阻抗与反射系数的关系为

(14)

其中Z为光学结构表面阻抗,Z0为真空中的阻抗,rR和rI分别为反射系数的实部和虚部.由此可分别计算光子晶体阻抗的实部和虚部.

2 数值结果

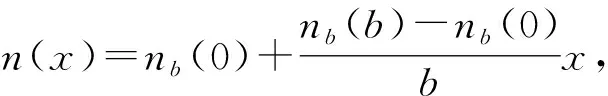
PCⅠ,PCⅡ及组合结构的反射率和阻抗虚部如图2所示.由图2(A)可见,PCⅠ在第1个带隙内阻抗虚部为负数.由图2(B)可见,PCⅡ在第1个带隙内阻抗虚部为正数,在第2个带隙内PCⅠ和PCⅡ均为负数.图2(C)给出了组合结构的反射率及PCⅠ和PCⅡ阻抗虚部求和的结果.由图2(C)可见,在第1个带隙内,Im(ZPCⅠ)+Im(ZPCⅡ)=0,且在第1个带隙内阻抗虚部之和为0的位置出现了界面态,而在第2个带隙内阻抗虚部之和不为0,未出现界面态.若增大计算波数范围,则由计算结果可知,在1,3,5等奇数带隙内PCⅠ和PCⅡ的阻抗虚部符号相反,在2,4,6等偶数带隙内PCⅠ和PCⅡ的阻抗虚部符号相同.因此,一维函数型反转对称组合结构的光子晶体仅奇数带隙存在界面态,偶数带隙不存在界面态.

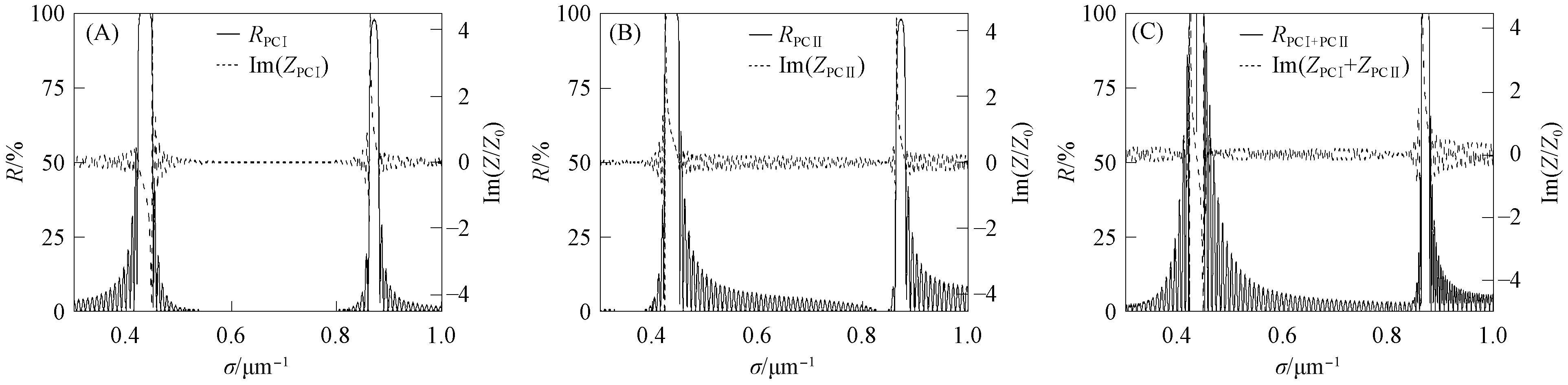
图2 PCⅠ(A),PCⅡ(B)及组合结构(C)的反射率和阻抗虚部Fig.2 Reflectance and imaginary part of impedance of PCⅠ(A),PCⅡ(B) and composite structure (C)

由于函数光子晶体具有起始值和终点值可调的特性,因此调节函数光子晶体端点值即可调节界面态的位置.当函数型介质B的折射率起始值分别为nb(0)=1.23,1.25,1.27时,组合结构的反射率和界面态如图3所示.由图3可见,当起始值逐渐增大时,在第3个带隙中禁带红移,禁带宽度增大,界面态位置随带隙移动而红移.当函数型介质B折射率终点值分别为nb(b)=1.30,1.32,1.34时,组合结构的反射率和界面态如图4所示.由图4可见,当终点值逐渐增大时,在第3个带隙中禁带红移,禁带宽度增大,界面态位置随带隙移动而红移.

图3 介质B折射率起始值为1.23(A),1.25(B),1.27(C)时组合结构的反射率和界面态Fig.3 Reflectance and interface states of composite structure when initial point values of refractive indexes of medium B are 1.23 (A),1.25 (B) and 1.27 (C)

图4 介质B折射率终点值为1.30(A),1.32(B),1.34(C)时组合结构的反射率和界面态Fig.4 Reflectance and interface states of composite structure when endpoint values of refractive indexes of medium B are 1.30 (A),1.32 (B) and 1.34 (C)

介质A厚度为585,615,665 nm时组合结构的反射率和界面态如图5所示.由图5可见,随着介质A厚度的增大,禁带红移,禁带宽度减小,界面态位置随带隙移动而红移.介质B厚度为355,385,405 nm时组合结构的反射率和界面态如图6所示.由图6可见,随着介质B厚度的增大,禁带红移,禁带宽度增大,界面态位置随带隙移动而红移.

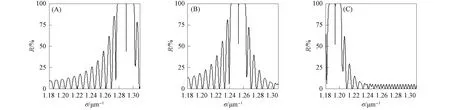
图5 介质A厚度为585(A),615(B),665 nm(C)时组合结构的反射率和界面态Fig.5 Reflectance and interface states of composite structure when thicknesses of medium A are 585 (A),615 (B) and 665 nm (C)

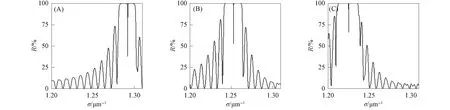
图6 介质B厚度为355(A),385(B),405 nm(C)时组合结构的反射率和界面态Fig.6 Reflectance and interface states of composite structure when thicknesses of medium B are 355 (A),385 (B) and 405 nm (C)

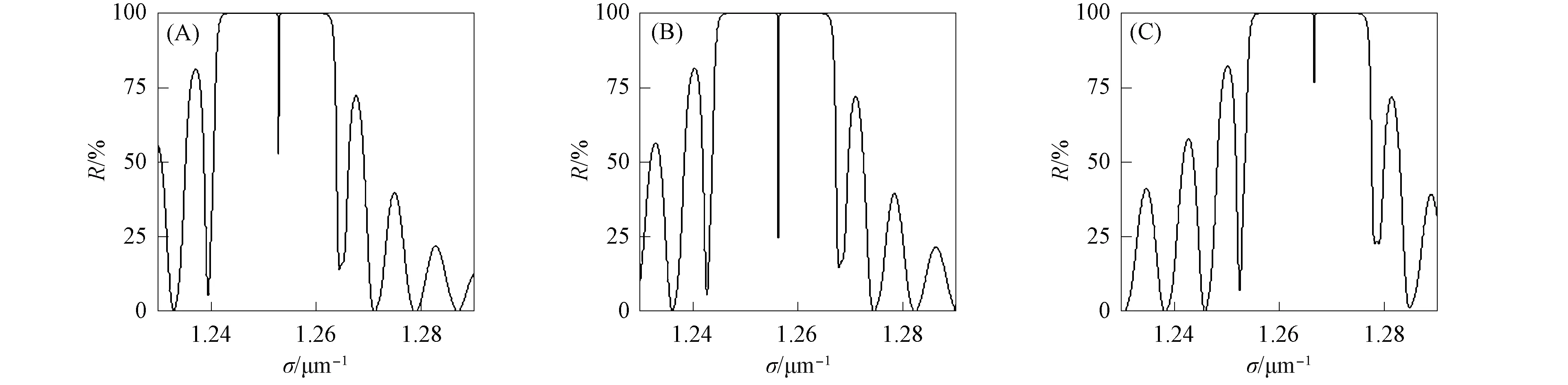
图7 入射角θ=0(A),π/36(B),π/18(C)时组合结构的反射率和界面态Fig.7 Reflectance and interface states of composite structure whenincident angles of θ=0 (A),π/36 (B) and π/18 (C)

入射角θ=0,π/36,π/18时组合结构的反射率和界面态如图7所示.由图7可见,随着入射角的增大,禁带蓝移,但宽度不变,界面态位置随带隙移动而蓝移.计算结果表明,当θ≥π/8时,界面态消失.

综上,本文研究了一维反转对称型函数光子晶体界面态,计算结果表明: 在总阻抗虚部为0的位置出现界面态; 对函数介质,当折射率的起始端点值增加时,带隙位置红移,界面态位置随带隙移动而红移,当折射率的终点值增加时,带隙位置红移,界面态位置随带隙移动而红移; 当常规介质A厚度增大时,禁带红移,禁带宽度减小,界面态位置随带隙移动而红移; 当函数介质B厚度增大时,禁带红移,禁带宽度增大,界面态位置随带隙移动而红移; 当入射角增加时,带隙位置蓝移,界面态位置随带隙移动而蓝移.因此,对反转对称型函数光子晶体,通过改变函数介质折射率端点值即可改变界面态位置,即反转对称型函数光子晶体的界面态具有可调节性.