基于K-medoids聚类算法的多源信息数据集成算法

祝 鹏,郭艳光

(内蒙古农业大学 计算机技术与信息管理系,内蒙古 包头 014109)

随着信息和电子网络社会的不断发展,人们生活和生产等各领域都存在各种信息,多数信息都依靠网络作为获取和分享载体,其拥有海量的信息资源,为满足用户的需求,根据信息的类型和功能分为不同的信息平台.但随着日益上升的数据量以及时刻都在更新变化的信息需求,各统计类、计算类、储存类等平台均受到一定程度的制约.而信息数据集成算法能高效解决上述问题,可将具有多元、异构的数据进行统一化集成管理,从而高效、快速地获取用户所需的信息.

文献[1]提出了一种基于适应高维海量数据的并行聚类集成算法,在数据采样阶段计算每个少数类样本的近邻值,再生成与该值相关的多个平衡数据集,将数据经过训练用于分类器上,分类后将平衡数据完成集成,该算法只对数量较少且较稳定的数据集有用,而在数量多且难度较大的数据上进行对比时,集成效果较差,实用性不强; 文献[2]采用一种基于迭代模糊聚类算法的集成模糊分类器,该分类器在第0阶段输出被扩充到原始空间的数据,以并行方式计算存在所有空间特征的数据,根据泛化原理将同特征数据集成到特定空间内,但该算法的适应能力较差,收敛速度较低,不能很好地消化过多的数据信息,导致集成次数相对较高.

针对上述问题,本文基于K-medoids聚类算法对多源信息数据集成方法进行改进.在进行数据集成前,先采用K-medoids聚类算法分析多源信息迁移学习特点,对数据样本的源域和目标域进行判定,得出变化规律和样本的初始权重值,解决了因关联不足而导致的集成效果较差问题,然后建立一个共识函数,得到两个数据之间的交互信息,对交互信息量较高的数据进行集成,以保证集成的准确性.实验结果验证了本文算法整体过程运算简单,逻辑表达清晰,解决了传统方法中存在的问题.

1 基于K-medoids聚类算法的多源信息迁移学习

本文集成算法采用K-medoids聚类[3]的学习框架,放宽了学习过程中易受测试与训练数据的约束限制[4].通过迁移学习分析数据源域与目标域之间的关联关系,根据关联程度[5],对存在数据的单域或双域进行划分,从而降低因判定失误导致的集成失败现象.

在迁移学习任务中,假设初始样本[6]的数据空间为G2,标记为X2∈{-1,+1}; 定义域[7]为T,该定义域T中包含少量带有原始特征标记的训练样本集合DT及不存在原始特征标记的样本集合DTEOT,所有数据均遵循PT概率进行分布.初始定义空间中存在Kn个源域SKn,各源域S1,S2,…,SKn中包含带有原始特征标记的数据为D1,D2,…,DKn,均遵循PD分布概率.将多源域[8]的数据通过合理利用,获取在目标域上的初始聚类模型为fS/D:G2→D,通过学习经验逐渐聚类并降低误差.

(1)

其中p(g,d)表示样本分布,Ω[·]表示在数据空间Ω中每次迁移产生的损失期望表示经过训练得到的第t次迁移学习中数据的源域SKn.采用损失估计[11]变换算法,计算该次迭代可能产生的经验误差,表达式为

(2)

通过式(2)判断可知,数据源判定算法在一定程度上进行了知识迁移,且对目标域和源域的判定结果较准确,能有效分辨二者之间存在的差异,对二者域之间的解释能力较强,可有效解决因关联不足而导致的负迁移[13]现象.

2 集成算法实现

(3)

交互信息平均值计算公式为

(4)

其中:φNMI表示交互信息的标准值;P表示交互信息数量;φm表示交互信息的覆盖值,φm值越大,表示包含在第m个聚类器中的信息含量越大.

根据该特点,通过权值因子集成两个覆盖值较高的数据,可保证集成的准确性[17],计算公式为

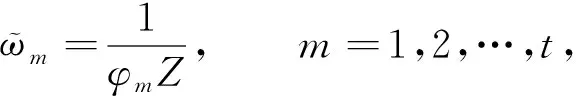
(5)

得到用于标准化Z值的权值因子为

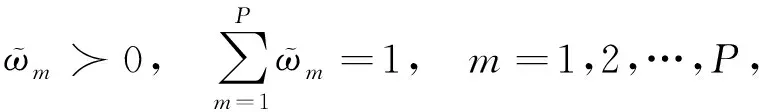
(6)

(7)

上述公式表明,通过聚类器得到集成结果的准确率高于不使用聚类器得到的集成结果,交互信息的权值是决定集成效果的重要因素,利用该方法完成的集成效果具有一定的精准性,整体流程如图1所示.

图1 多源数据信息集成方法流程框架Fig.1 Process framework of multi-source data information integration method

3 仿真实验

3.1 实验设置

本文实验所需的所有训练数据均来自UCI机器学习数据库.在数据库中挑选1 000个不同种类的数据样本,采用ECE(electrical and computer engineering)软件对所有数据样本进行统一集成.选择文献[1]提出的适应高维海量数据的并行聚类集成算法和文献[2]提出的基于迭代模糊聚类算法与本文算法进行对比分析,验证本文算法的有效性.3种集成算法存在的共同点: 所生成的聚类器数量都在1～2内,表明迭代步数的最大值为400,当数据量不断上升超出既定值时,不会出现迭代停止的现象,在规定的迭代次数内对比3种算法可集成的数据量.为提高实验结果的准确性,分别在3个不同的数据集上进行实验,对比集成效果.3个数据集的信息列于表1.

表1 不同数据集的信息

3.2 基于NMI的集成结果判定

以标准互联网归一化互信息NMI作为判定集成效果的评估准则,该指标是将信息进行量化度量的结果,也可理解为目标信息出现的概率,计算公式为

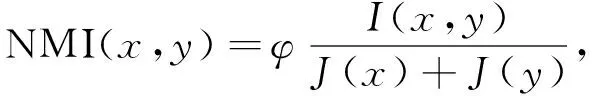
(8)

其中I(x,y)表示全部集成数据,φ表示度量系数.NMI值越大表示集成效果越好,NMI值越小表示集成效果越差.在3个数据集上不同算法的NMI值变化曲线分别如图2～图4所示.由图2～图4可见: 数据集Leukaemia和数据集Vehicle的NMI值变化曲线较相似,3种算法的曲线走势均呈下降趋势,但较缓慢,存在缓冲位置; 而数据集Ecoli则存在相反变化,3种算法曲线均存在急剧下降趋势.这是因为数据集Ecoli中的信息种类较繁杂,同一类别的信息不处于同一标签内,涉及面广、覆盖率大,集成的难度较高,所以该数据集(图4)的集成结果更具代表性,更能体现算法的优异程度.

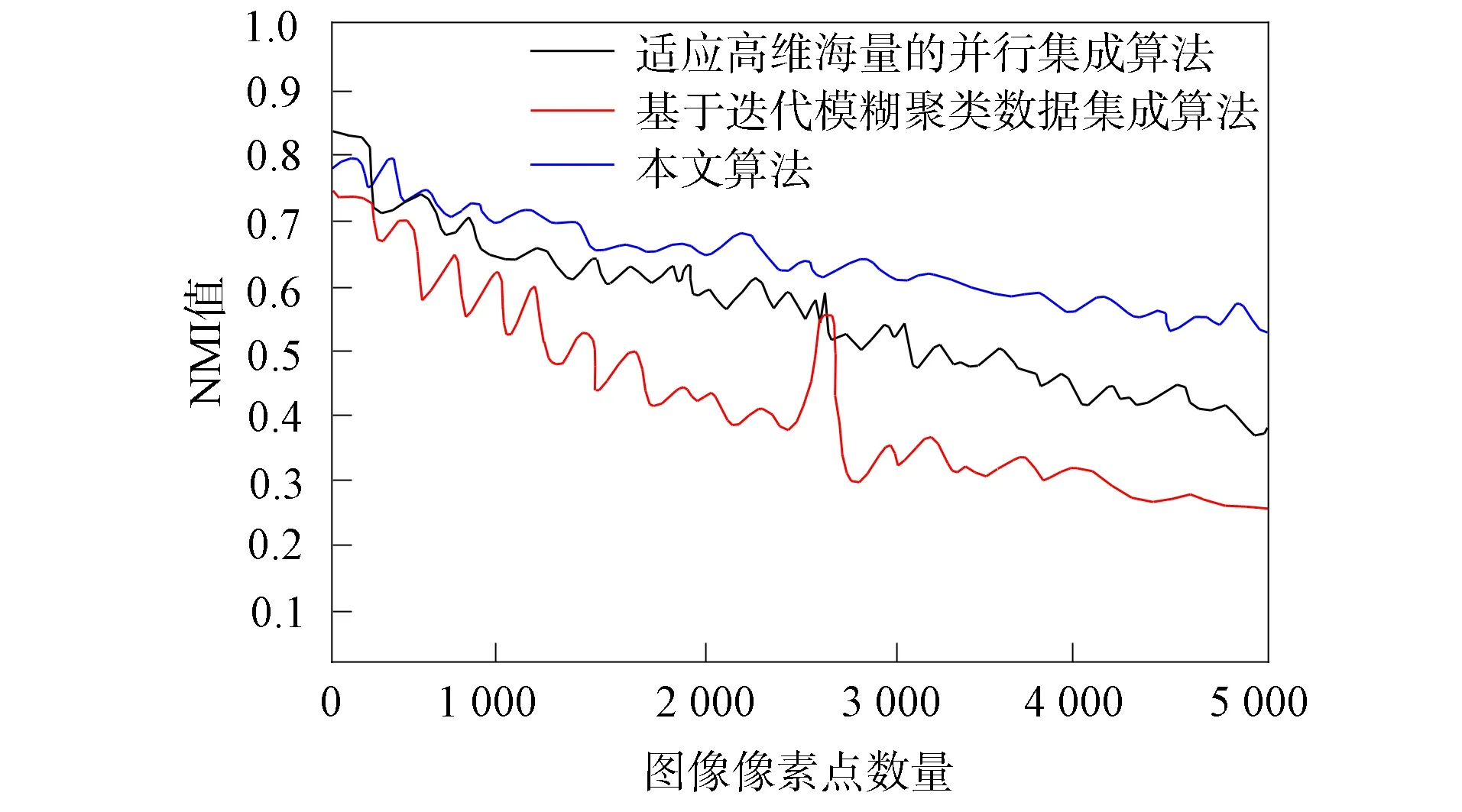
图2 在数据集Leukaemia上的NMI值变化曲线Fig.2 Change curves of NMI values on Leukaemia dataset

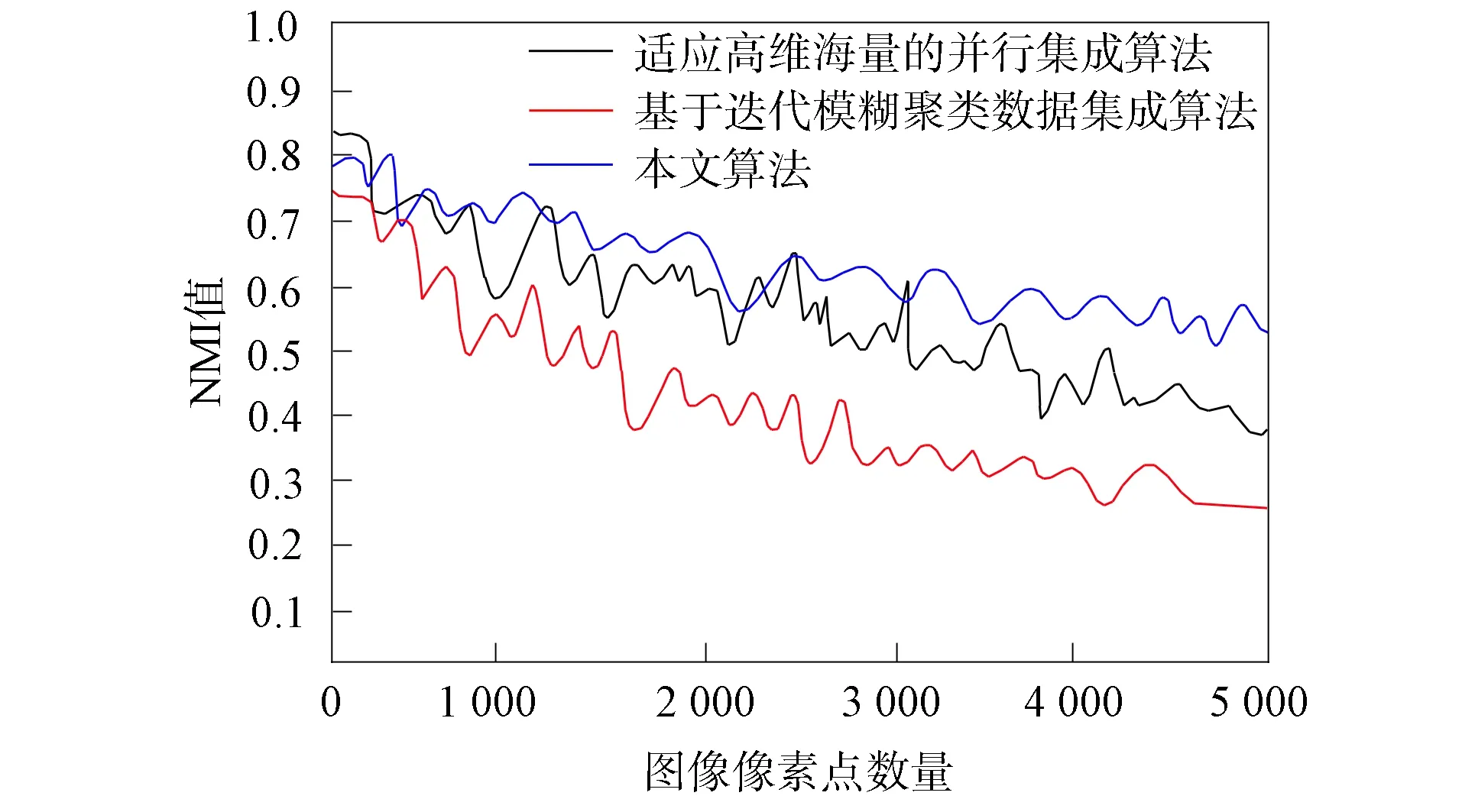
图3 在数据集Vehicle上的NMI值变化曲线Fig.3 Change curves of NMI values on Vehicle dataset

由图4可见,当集成数量不断增加时,本文算法曲线趋于前平后降的小幅度变化趋势; 而另外两种算法则存在不稳定的下降趋势.表明在种类较繁杂且不稳定的数据集上,本文算法最具优势,在只选择少数且高质量的数据比对时,3种算法差距不明显,但选择数量多且难度较大的数据对比时,本文算法的集成质量较高.这是因为本文算法在对特定的子集时,采用了特征查找法,通过预先标记的特征标签进行系统搜索,在最短的时间内聚类所有信息,具有灵活性和较强的适应能力.

3.3 二次集成次数对比分析

由于信息的种类较多样化,存在的干扰因素过多,因此算法能否在最少的集成次数下达到既定标准,也是验证集成能力的重要指标.3种算法二次集成次数对比曲线如图5所示.由图5可见,本文算法所需的次数曲线最低,所需次数均在可承受范围内,而另外两种算法的二次集成次数过多,说明算法的适应能力较差,收敛速度较低,不能很好地消化过多的数据信息.这是因为针对非稳定数据集,一般存在无偏差和有限偏差两种概念,两种对比算法在进行集成时忽略了外界因素导致的有限偏差,只考虑了信息自身可能产生的影响,导致限制较大,集成效果较差.

图4 在数据集Ecoli上的NMI值变化曲线Fig.4 Change curves of NMI values on Ecoli dataset

图5 3种算法二次集成次数对比曲线Fig.5 Comparison curves of secondary integration times of three algorithms

综上所述,为实现多源信息数据在信息种类繁杂且数据较多的环境下高效集成,本文提出了一种基于K-medoids聚类算法的多源信息数据集成方法.先通过分析计算不同种类数据的迁移学习率帮助后续的聚类集成,能更快、更精准地查找到目标区域,并实现划分; 然后对源点较多、较杂的数据,利用K-medoids聚类算法从数据的特征域和数据的源域两方面解决源域问题,分析二者之间的差异性,通过损失函数不断迭代修正偏差量,直至查找到准确源,实现高质量集成.仿真实验结果表明,本文算法无论在何种环境下都能保证集成效果,适应能力较强且收敛速度快,二次集成概率小,性能优异.