具有恐惧效应的时滞捕食者-食饵模型
王 灵 芝
(陕西师范大学 数学与统计学院,西安 710119)
0 引 言
捕食者和食饵之间的相互作用是数学生态学和进化生物学的一个核心问题.研究表明,捕食者通过直接杀戮可对食饵的种群数量产生直接影响[1-4],但每个物种也会对感知到的捕食风险作出各种反捕食反应[5-11],包括栖息地、觅食、警惕性和生理的变化等.基于文献[11-12]的工作,本文考虑具有恐惧效应、种内竞争和捕食后生物量从食饵转化到捕食者的时间延迟以及在转化过程中捕食者的死亡率等因素的捕食者-食饵模型:

(1)
其中:u(t)和v(t)分别表示食饵和捕食者t时刻的种群密度;r为食饵的出生率;d和μ分别为食饵和捕食者的自然死亡率;a和α分别为食饵和捕食者因种内竞争而导致的死亡率;f(k,v)为恐惧因子,表示由于恐惧而导致的反捕食行为成本,k反映了驱动食饵反捕食行为的恐惧程度;β和τ分别为捕食后生物量从食饵转化到捕食者的转化率和时间延迟; e-sτ为捕食者在生物量转化过程中的存活率;g(u)为功能反应函数,且∀u≥0,g(u)∈C(),g(0)=0,g′(u)>0.根据k和f(k,v)的生物学意义,本文做如下合理假设[10-11]:
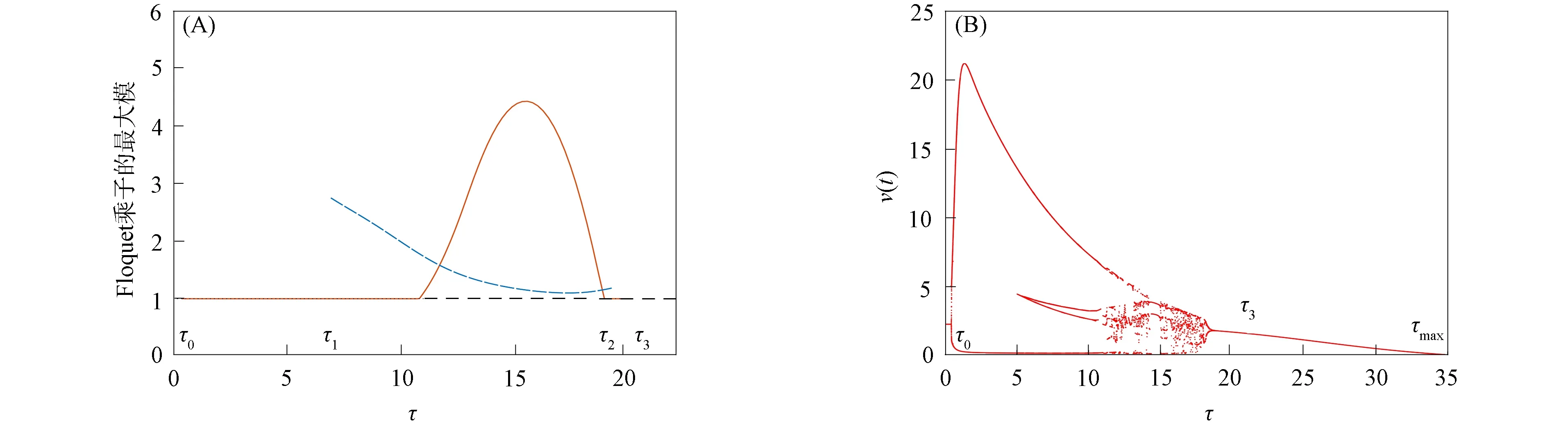
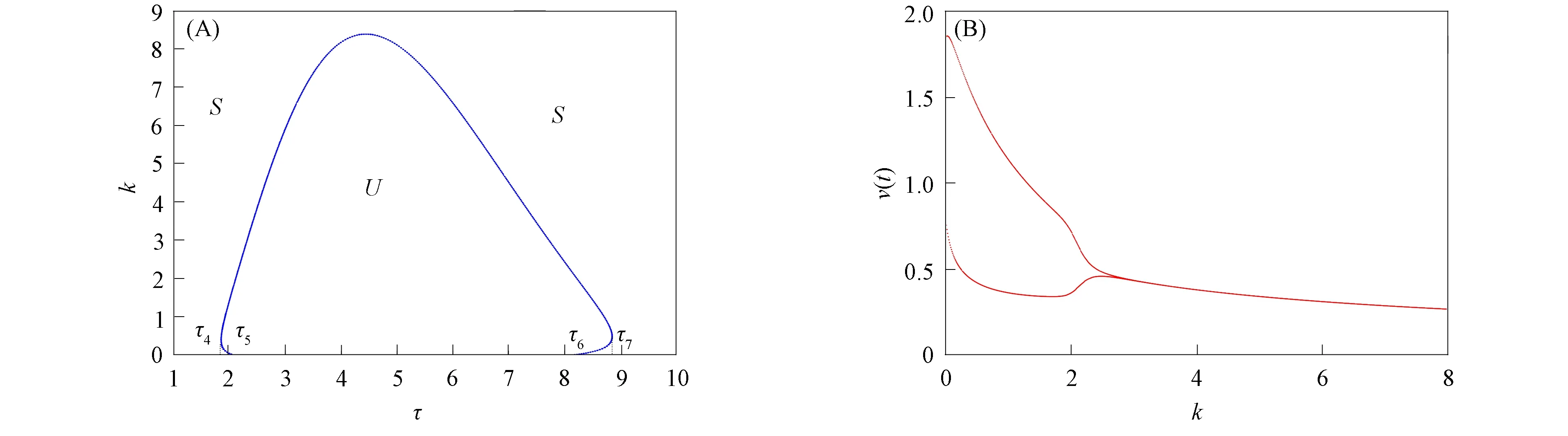
由文献[10]可知,当r (H2)r>d. 当τ>0时,记C∶=([-τ,0],),其中C为从[-τ,0]映射到的连续函数全体构成的Banach空间.对∀φ∈C,定义范数记C+∶=([-τ,0],+)为C的非负锥.当t=0时,系统(1)的初始条件为 φ∈X∶=C+×C+. (2) 定理1在初始条件(2)下,系统(1)的解具有非负性和最终有界性.即所有轨线最终进入并保持在如下有界不变区域中: 证明: 由系统(1)的第一个方程得 从而可得 对于v的非负性,可利用反证法.假设t1>0是使得v(t)第一次为0的时刻,即v(t1)=0.由系统(1)的第二个方程可知 v′(t1)=βe-sτg(u(t1-τ))v(t1-τ)>0, 故存在ε>0,使得当t∈(t1-ε,t1)时,有v(t)<0.与当t∈[0,t1)时,v(t)>0矛盾,故v(t) ≥0. 下证最终有界性.由系统(1)的第一个方程及条件(H1)可知, u′(t)≤rf(k,v)u-du-au2≤(r-d)u-au2, 其中δ=min{r-d,μ}.故 (3) (4) 定理21) 若R(τ)≤1,则Eb是局部渐近稳定的,进一步,Eb在Γ{u=0}内是全局渐近稳定的; 2) 若R(τ)>1,则Eb是不稳定的. 证明: 1) 显然特征方程(4)有一个特征根λ1=-(r-d)<0,其他根由方程 (5) 考虑Lyapunov泛函[12]: 计算其沿系统(1)的导数为 2) 若R(τ)>1,则由文献[13]中引理6可知式(5)存在一个正实部特征根,从而Eb是不稳定的. (6) 下面讨论当R(τ)>1时系统(6)共存平衡点E*=(u*,v*)的稳定性.共存平衡点E*满足的方程为 a2v2+a1v+a0=0, (9) 其中 a2=k(aαesτ+c2β)>0,a1=aesτ(α+μk)+cβ(dk+c)>0,a0=aμesτ+cβ(d-r)<0. λ2+b1λ+b0+(c1λ+c0)e-λτ=0, (10) 其中 b1=μ+2αv*+au*>0,b0=au*(μ+2αv*)>0, 由于 故0不是方程(10)的特征根.当τ=0时,系统(6)变为如下常微分方程: (11) 证明: 当τ=0时,在共存平衡点E*处的特征方程(10)变为 λ2+(b1+c1)λ+(b0+c0)=0, (12) 其中 b1+c1=au*+αv*>0,b0+c0>0. 由Routh-Hurwitz准则可知式(12)的根均具有严格负实部,即当τ=0时,E*=(u*,v*)是局部渐近稳定的. 下面考虑当τ>0时,特征方程(10)纯虚根的存在性.假设λ=iω(ω>0)是方程(10)的一个根,将λ=iω代入方程(10)并分离实部和虚部可得 对方程(13)和(14)两端取平方再相加,可得 (15) 其中 记 J(τ)=b0(τ)-c0(τ),I-={τ∈(0,τmax):J(τ)<0},I+={τ∈(0,τmax):J(τ)≥0}. 若I-=Ø,则对∀τ∈(0,τmax),均有b0≥c0,即式(15)不存在正根,因此对∀τ∈(0,τmax)没有纯虚特征根穿过虚轴,且式(10)的根始终保持在虚轴左侧,故∀τ∈[0,τmax),共存平衡点E*是局部渐近稳定的.若I-≠Ø ,则∃τ*∈I-,使得b0(τ*) (16) 从而特征方程(10)存在纯虚特征根λ=iω(τ*),且纯虚特征根需满足 (17) (18) 可知iω*(τ*)是特征方程(10)的纯虚根当且仅当τ*为函数Sn的零解.由文献[16]有 注意到 因此关于横截条件的结论如下: 引理1若∃τ*∈I-满足Sn(τ*)=0(n∈),则当τ=τ*时,式(10)具有一对共轭纯虚根λ(τ*)=±iω*(τ*).进一步,若则在复平面上这对纯虚根随着τ的变化从左至右穿过虚轴; 反之,若则其从右至左穿过虚轴,其中 由式(18)可知Sn(0)<0,且对∀τ∈I-,有Sn(τ)>Sn+1(τ),其中n∈.记 假设(H3)可保证存在一个K∈+,使得当0≤i≤K-1(i∈)时每个Si(τ)存在两个单根,记为τi和τ2K-i-1,且当i≥K时,Si(τ)没有零点,则对于所有的n∈,Sn(τ)只有2K个简单的零点τi,且进一步,引理1表明,对于每个0≤i≤K-1(i∈),有从而一对纯虚特征根±iw(τi)从左至右穿过虚轴,另一对纯虚特征根±iω(τ2K-i-1)从右至左穿过虚轴.因此当τ=τj(0≤j≤2K-1,j∈)时,系统(6)在E*处经历了Hopf分支.进一步,当τ∈[0,τ0)∪时E*是局部渐近稳定的,当τ∈(τ0,τ2K-1)时E*是不稳定的. 记Tj为在τj处分支出周期解的周期,对于0≤i≤K-1(i∈),有 因此,利用时滞微分方程Hopf分支理论[15],可得如下关于E*的稳定性和局部Hopf分支的存在性结论. 定理4对于系统(6),如果R(τ)>1且I-≠Ø ,则下列结论成立: 下面利用Wu[17]提出的全局Hopf分支定理讨论系统(6)的全局Hopf分支.令x(t)=(u(τt),v(τt))T,则系统(6)可写成如下泛函微分方程: (19) (20) (21) 当R(τ)>1时,0不是系统(19)任何驻解的特征值,故文献[17]中条件(A2)成立.由式(20)知文献[17]中光滑性条件(A3)成立. 由上述讨论可知,∀j∈[0,2K-1],驻解为(E*,τj,2π/(ωjτj)),其中j∈是系统(19)的孤立中心[17],ωj=ω(τj)是G(ω,τ)=0的唯一正根,如式(16)所示,且只有一对形式为的纯虚特征根,其中由引理1可得每个中心处的横截数[17]为 (22) 记C(E*,τj,2π/(ωjτj))⊂Σ(F)是过(E*,τj,2π/(ωjτj))的连通分支,其中j∈[0,2K-1],j∈.由局部Hopf分支定理4可知,C(E*,τj,2π/(ωjτj))是Σ(F)的非空子集. 为进一步给出存在周期解的τ区间,需证明系统(19)的一些性质. 引理2系统(19)的所有非平凡非负周期解x(t)一致有界.即对∀t≥0,有0 (23) 证明: 系统(19)是由系统(6)经无量纲变化所得,因此系统(19)的所有非平凡非负周期解x(t)等价于系统(6)的非平凡非负周期解u(t),v(t).下证系统(6)的非平凡非负周期解u(t),v(t),对∀t≥0有0 因为u(t)是非平凡非负的周期解,故存在t0>0,使得u(t0)>0.对u′(t)积分可得 则∀t>t0,u(t)>0.又因为u(t)具有周期性,故∀t>0,u(t)>0.再由u(t),v(t)是非平凡非负的周期解,可得 并存在t1>0,使得v(t1)>0.考虑初值问题 (24) 问题(24)的解为 由比较原理知当t>t1时,v(t)≥y(t)>0,又因为v(t)具有周期性,故∀t>0,v(t)>0. 其中T是周期解的周期,与u(t)最终有界矛盾,因此M为u(t)的一致上界.同理,M为v(t)的一致上界. 引理3系统(19)不存在周期为1的非平凡周期解. 证明: 反证法.设x(t)是系统(19)周期为1的非平凡周期解,则(u(t),v(t))为系统(6)周期为τ的非平凡周期解,故u(t-τ)=u(t),v(t-τ)=v(t),因此(u(t),v(t))也为常微分方程(11)的周期解,但由定理3知系统(11)不存在周期解,矛盾.从而系统(19)不存在周期为1的非平凡周期解. 定理5对∀j∈[1,2K-2](j∈+),关于系统(19)下列结论成立: 1) 所有的连通分支C(E*,τj,2π/(ωjτj))是有界的; 2) 两个全局Hopf分支C(E*,τn,2π/(ωnτn))和C(E*,τ2K-n-1,2π/(ω2K-n-1τ2K-n-1))相连,连接一对Hopf分支值τn和τ2K-n-1.进一步,对于每个τ∈(τn,τ2K-n-1),系统(19)至少存在一个周期属于(1/(n+1),1/n)的周期解,其中1≤n≤K-1,n∈+. 证明: 根据引理2可知C(E*,τj,2π/(ωjτj))在X上的投影有界.又因为系统(19)不存在周期为1的周期解,故对∀m∈+,系统(19)不存在周期为1/m或1/(m+1)的周期解.由定理4可知,对∀n∈[1,K-1],n∈+,在连通分支C(E*,τn,2π/(ωnτn))(resp.C(E*,τ2K-n-1,2π/(ω2K-n-1τ2K-n-1)))上周期解的周期Tn满足 故对∀j∈[1,2K-2](j∈+),C(E*,τj,2π/(ωjτj))在T-空间上的投影有界.又因为为有界区间,所以对∀j∈[1,2K-2](j∈+),C(E*,τj,2 π/(ωjτj))在+上有界. (25) 图1 函数S0,S1,S2在区间上的图像(A)和系统(19)所有的全局Hopf分支(B)及其周期解的周期(C)Fig.1 Images of functions S0,S1,S2 on (A),all global Hopf bifurcations of system (19) (B) and periods of periodic solutions (C) 当分支参数τ在更大范围内变化时,全局Hopf分支由局部Hopf分支从Hopf分支值延拓而得.图1(B)为两个全局Hopf分支C(E*,τk,2π/(ωkτk))(0≤k≤1),且每个全局Hopf分支连接了一对Hopf分支值.图1(C)为全局Hopf分支中周期解的周期.由图1(C)可知,∀τ∈(τ1,τ2),系统(19)至少在全局Hopf分支C(E*,τ1,2π/(ω1τ1))上存在一个周期为T1∈(τ/2,τ)的周期解,因此与定理5结论相符. 图2(A)为两个全局Hopf分支上周期解Floquet乘子的最大模,以反映周期解的稳定性.由图2(A)可见,第一支全局Hopf分支C(E*,τ0,2π/(ω0τ0))上的周期解随着τ的增加呈现“稳定-不稳定-稳定”的状态变化,第二支全局Hopf分支C(E*,τ1,2π/(ω1τ1))上的周期解均为不稳定状态.图2(B)为以τ为分支参数的分支图,进一步验证了定理4以及图2(A)中周期解的性质.当τ∈[0,τ0)∪(τ3,τmax)时,唯一的共存平衡点E*是局部渐近稳定的; 当τ∈(τ0,τ3)时,E*是不稳定的,并产生Hopf分支,且Hopf分支上的周期解从稳定状态转入混沌状态又恢复稳定状态.此外,当τ>τmax≈34.778时,系统(19)不存在共存平衡点,此时边界平衡点Eb全局渐近稳定. 图2 Hopf分支上周期解Floquet乘子的最大模(A)及以τ为分支参数的分支图(B)Fig.2 Maximum modulus of Floquet multipliers of periodic solutions on Hopf bifurcations (A) and bifurcation diagram with τ as bifurcation parameter (B) 为分析恐惧程度k和时滞τ对系统(19)的综合影响,基于文献[10-11]的数值模拟选择如下一组参数:r=0.6,d=0.05,a=0.05,c=0.4,β=0.5,s=0.16,μ=0.08,α=0.05.利用DDE-BIFTOOL工具包绘制双参数Hopf分支,如图3(A)所示.由图3(A)可见,在区域S中共存平衡点E*局部渐近稳定,在区域U中共存平衡点不稳定,且在E*附近发生Hopf分支,存在周期解.由图3(A)可知: 当时滞τ较小(τ∈[0,τ4))或较大(τ∈(τ7,τmax))时,恐惧程度k对系统(19)的稳定性无影响,当时滞τ∈(τ4,τ7)时,系统(19)的稳定性将受食饵对捕食者恐惧的影响,当捕食者引起的恐惧处于低水平时,E*不稳定,产生Hopf分支,当捕食者引起的恐惧处于高水平时,E*为稳定状态.图3(B)为在选取τ=2.3∈(τ5,τ6)时,k作为分支参数的分支图.由图3(B)可见: 当k较小时,E*不稳定,在其附近产生稳定的周期解; 当k较大时,E*又恢复稳定状态.对这种现象的合理生物学解释[18]是: 当食饵非常害怕捕食者时,它们会减少觅食活动并适应不同的防御机制以避免被捕食.恐惧效应可极大地帮助捕食者物种增加其生物量,因此,从长远来看,还有助于捕食者物种的持久性并提高整个系统的稳定性. 图3 以k,τ为分支参数的双参数Hopf分支图(A)及当τ=2.3∈(τ5,τ6)时k作为分支参数的分支图(B)Fig.3 Two parameters Hopf bifurcation diagram with k and τ as bifurcation parameters (A) and bifurcation diagram with k as bifurcation parameter when τ=2.3∈(τ5,τ6) (B)1 适定性与可行平衡点


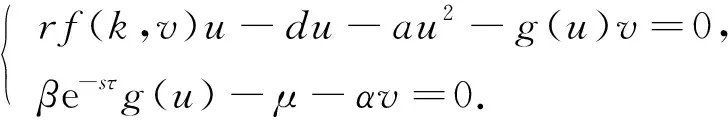
2 边界平衡点的全局稳定性




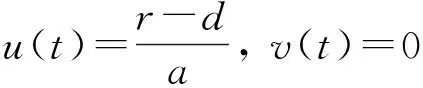
3 共存平衡点的稳定性与局部Hopf分支


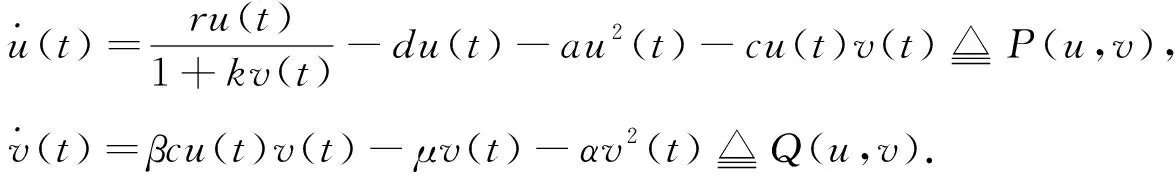




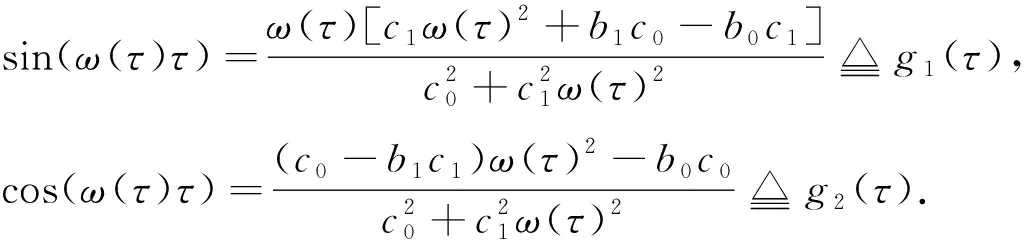



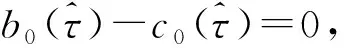


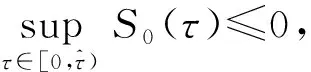

4 全局Hopf分支







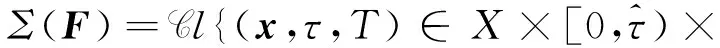




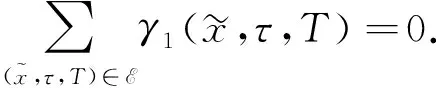
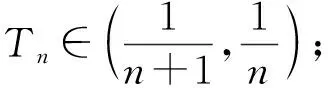
5 数值模拟