篮子期权定价的深度学习方法
张 宁 涂宇彬 郑亦超 陈梦圆
一、引言
期权作为金融市场上交易频繁的一类产品,具有锁定标的资产未来交易价格的功能,在一定程度上降低了交易双方的风险。除了常见的欧式期权与美式期权,市场上还存在着一大类奇异期权,包括复合期权、回望期权以及一些嵌入式结构债券等,这些期权的合约要求更加复杂,从而导致对应的定价问题难度大幅度提升。考虑到近十多年机器学习在算力提升的支持下开始应用于许多领域并展现出了优势,将其应用于复杂期权的定价逐渐成为金融的一个关注领域,本文的工作也由此展开。具体来说,本文将从高维衍生品——篮子期权的定价问题入手,将这一问题抽象为偏微分方程终值问题,并用深度倒向随机微分方程(Backward stochastic differential equation,BSDE)方法来对这一问题进行求解。
由于金融市场中金融产品的价格很多都与期权定价有关,期权定价问题成为经典的金融工程问题。但因为期权本身作为一种金融衍生工具,其价值受时间与标的资产价值波动影响,且将数学方法与思想引入解决金融问题的想法出现的时间也比较晚,因此期权定价的方法始终难有一套标准。直到20世纪末,BS期权定价模型(Black和Scholes,1973[1];Merton,1973[2])的推出才使得期权定价问题有了突破口。随后,诸多学者在此基础上针对不同种类的期权,在不同的假设条件下提出了更多的期权定价模型。其中大部分模型都表示成偏微分方程或偏微分方程组的初(终)值问题,但往往缺少较好的通用解决方法,难以获得解析解,且随着待解决问题难度的逐渐加深,“维度诅咒”对偏微分方程的实际应用影响越来越难以忽视,即随着待求解目标函数的变量维数增加,求解问题的计算成本呈指数型增长,如何有效且准确地寻找解析解成为研究热点。在Pardoux和Peng(1990)[3]提出倒向随机微分方程的一般形式并给出解的存在唯一性证明后,BSDE与偏微分方程和随机控制问题的深度联系引起了许多数学家的兴趣,从而在以抛物型偏微分方程形式为主的金融衍生品定价领域,有了BSDE的一席之地。由此诸多学者试图借助BSDE来更高效地求解偏微分方程问题,如Han等(2018)[4]构建了一个结构明晰的神经网络用于求解高维非线性抛物线型偏微分方程在t=0时的边界解,开创性地将原问题转换为BSDE的形式,并引入布朗运动将连续时间上的方程离散化,并取得了理想结果。此外,Fujii等(2019)[5]、Henry-Labordere(2017)[6]、Elbrächter等(2018)[7]也利用BSDE获得了一定的研究成果,为本文研究思路提供了启示。
深度学习作为新一代人工智能的核心技术,试图利用层次结构来学习数据中的高级抽象,已在处理图像、视频、语音和音频方面取得了突破性进展,而如今芯片处理能力(如图形处理器GPU单元)的显著提高、计算机硬件成本的显著降低,以及机器学习算法的显著进步,都使得深度学习发展更加迅速。且深度学习能够实现标准计量经济模型无法实现的“非线性”,即能够高精度地学习几乎任何函数的特性,也使得其在金融领域有着广泛的应用空间。其中金融市场数据非常丰富,训练一种算法来“学习”市场中生成期权价格的函数是可行的,这在Malliaris和Salchenberger(1993)[8]、Hutchinson等(1994)[9]的研究中得到了验证,而后诸多学者开始关注深度学习在期权定价中的应用,如Amilon(2003)[10]、Culkin和Das(2017)[11]、谢和亮和游涛(2018)[12]、孙有发等(2021)[13]均在该方向上获得了理想的成果。
本文在这些研究的基础上,将以上述基于BSDE的深度学习架构下的神经网络模型为工具求解Zhao和Li(2020)[14]一文中的终值问题,一方面与该文中的数值解做横向比较,另一方面进行不同神经网络参数调整情况下的自身比较。
本文剩余部分结构如下:第二部分介绍期权定价模型和BSDE的预备知识,并对基于BSDE的神经网络模型做较为详细的讲解;第三部分进行模型分析、改进和数值试验,并对模型的表现进行评估;第四部分总结了本文方法在更高维度上的优势,并对主要内容以及研究方法的应用可能性进行了总结。
二、定价模型与方法
(一)期权定价的预备知识
1.传统BS模型。
本节将对BS微分方程以及BS定价公式做一个简单的介绍。以标的资产为股票的期权为例,在一系列假设的前提下,可以用布朗运动来对股票价格变动进行刻画,同时,期权价格取决于股票价格,也就是说,可以将期权视作一个随机过程的函数。而伊藤引理则提供了对随机过程函数进行微分处理的理论基础,在此之前,没有一个很好的处理该问题的方法。借助伊藤引理,可以得到期权等衍生品价格的随机微分方程,求解后即可得到期权价格的定价公式,而现在为各界所熟知的BS定价公式就是一个简单的用例。
在BS公式的推导过程中,假设股票价格St满足dSt=μStdt+σStdWt,其中Wt是标准布朗运动,令欧式看涨期权价格为C,它是股价和时间的函数,可记作C(St,t),对C(St,t)运用伊藤引理可得:
(1)
股票价格St作为一个伊藤过程,其函数期权价格C也是一个伊藤过程,且二者的随机性来自同一个布朗运动Wt,这样就可以通过建立投资组合的方法来消除这一随机项的影响,从而得到BS微分方程:
(2)
欧式看涨期权在到期日时的价格为CT=max(ST-K,0),其中K为交割价,加上这一终值条件后便可以得到偏微分方程的终值问题:
(3)
现在,只需要求解这一终值问题,就能得到期权定价公式,但偏微分方程的解析解往往难以求得。在标的是单个资产的情况下,绕过这个偏微分方程,求解上述问题的方法就有很多种,比如等价鞅测度变换、风险中性定价理论等。由于本文重点不在于对这些方法的阐释,故这里将不对这些方法进行展开。本文要研究的问题,是当标的为资产组合时,如何求解这一终值问题。
2.篮子期权定价模型。
篮子期权,是标的为一篮子资产的期权,常被用作对这一篮子资产的套期保值操作。与单标的期权不同的是,篮子期权的收益情况由这些资产价格的加权算术平均决定,且其价格通常比单个资产的期权组合价格要低,因而一份篮子期权要比将篮子中资产单个组成期权组合在应用上更具效率。具体来说,由于资产之间相关性的存在,资产组合总是比单个资产更具有稳定收益,这就是篮子期权的一大优势。但是多个资产的情况要比单资产复杂,在定价时篮子期权会有一些不同的特征,以下本文将详细介绍篮子期权的定价模型。

(4)
以下进行篮子期权的BS公式推导。设第i个标的资产在t时刻价格为Si(t),i=1,…,d,且每个标的资产的价格,其变化均服从几何布朗运动,即满足如下随机微分方程:

(5)
其中:μ=(μ1,μ2,…,μn)T为常值向量,是预期收益率向量;σi为常数,是收益的波动率;Wi(t)是一维标准布朗运动,这些布朗运动之间有一定的相关性,具体如下:
E[Wi(t))=0,Var(Wi(t)]=t,
Cov[Wi(t),Wj(t)]=ρijt,i≠j
(6)
将随机微分方程以矩阵形式表示如下:
(7)
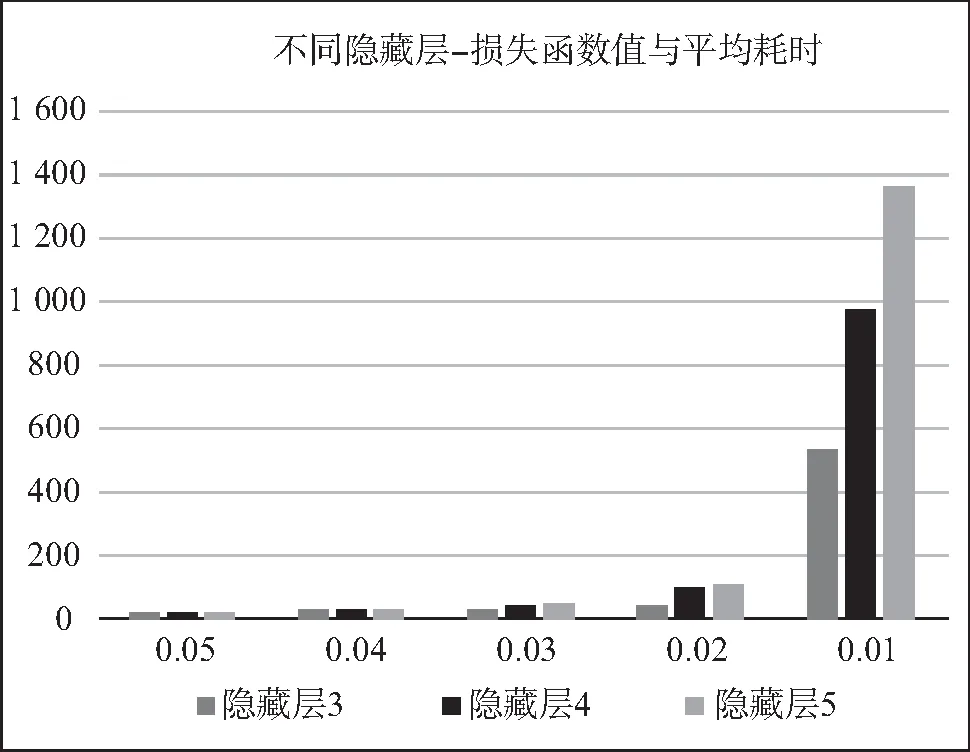
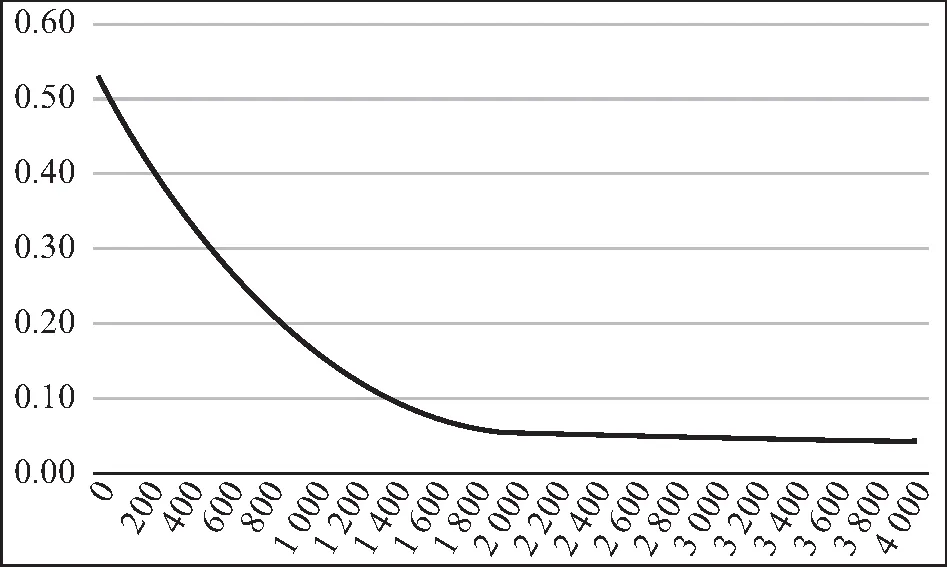
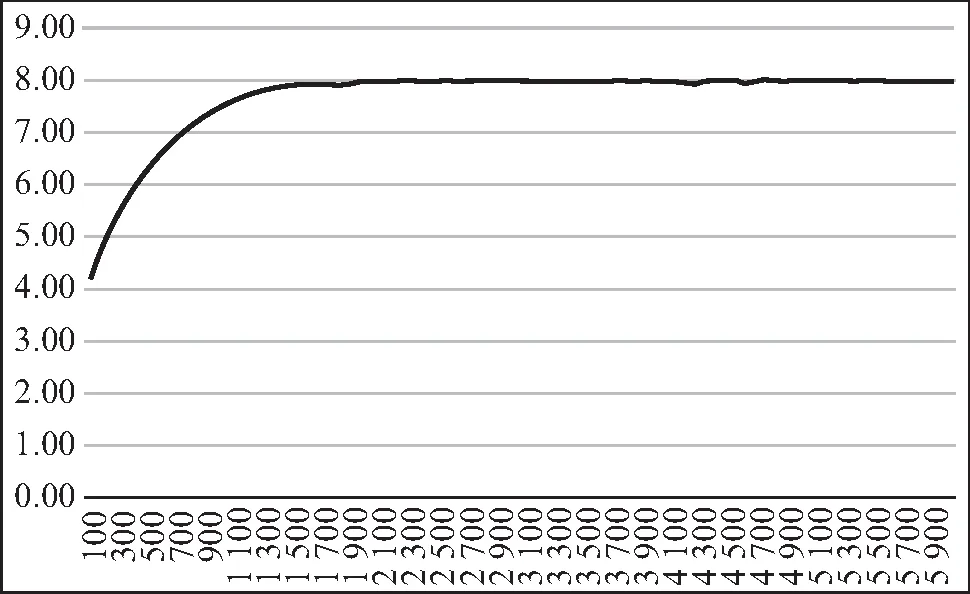
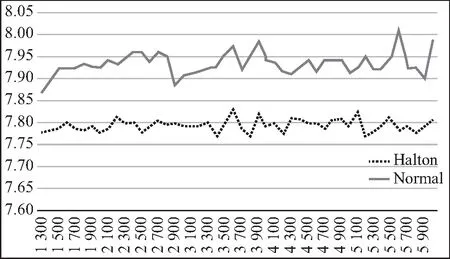
记W(t)=(σ1W1(t),σ2W2(t), …,σdWd(t))T,则根据定义可知W(t)为d维布朗运动,其协方差阵为Σ={Cov[W(t)]ij=ρijσiσj, 0 (8) 那么,随机微分方程式可写作如下形式: (9) 这样就得到了一篮子中每个资产满足的随机微分方程的另一种形式,这种形式考虑到了各资产之间的相关性: (10) 其中,Bj(t)是相互独立的标准布朗运动。 接下来,利用多维伊藤公式得到关于篮子期权价值V的随机微分方程: (11) (12) 最后加上终值条件,得到篮子期权定价的BS模型: (13) 1.BSDE方法论。 本文使用的倒向随机微分方程,对求解这一类偏微分方程有着更加显著的效果。BSDE来源于伊藤随机微分方程理论无法解决的一类问题:倒向随机问题。比如在金融数学里,如果给出未来某个时间点的风险值,通过建立恰当的随机模型,来确定出当前需要的初始值,这就是典型的倒向随机微分方程模型。与正向随机方程不同的是,倒向随机方程的解不再是单纯的状态变量Y,而需要添加一个扰动项Z,使得(Y,Z)构成方程的解。这里的随机函数Z具有调控作用,类似于控制论中的控制函数,它保证了方程的解Y是适应的。根据一般化的Feynman-Kac 公式[15],倒向随机微分方程的解与非线性偏微分方程的解之间有着极其深刻的关系,这为本文求解篮子期权的BS模型提供了十分便利的途径和技巧。 篮子期权定价使用的本质是如下高维半线性抛物线型偏微分方程 (14) 求解上述偏微分方程的思路就在于将其转化成BSDE的解。令{Bt}t∈[0,T]为一个n维标准布朗运动,{Xt}t∈[0,T]为由{Bt}t∈[0,T]生成的一个随机过程,满足如下形式: (15) 这样,偏微分方程的解满足如下的倒向随机微分方程: σ(s,Xs)dBs,t∈[0,T] (16) 连续的积分式难以求解,常见的做法是将时间区间[0,T]离散化0=t0 (17) (18) 其中: Δtk=tk+1-tk, ΔBk=Btk+1-Btk 随后可以得到如下两个迭代式: Xtk+1-Xtk≈μ(tk,Xtk)Δtk+σ(tk,Xtk)ΔBk (19) u(tk+1,Xtk+1)-u(tk,Xtk) (20) 上述两个迭代式传达出这样的一种思想:从Xt0=ξ,u(t0,Xt0)=u(0,ξ)出发,经过迭代,可以得到函数u在(t=tN=T,x=XtN)处的值,但目前已知条件是终值条件,函数的初值是目标解,看似这个迭代式并不能起到作用,本文将引入蒙特卡洛模拟的思路和神经网络的架构来应用该迭代式,求解这一BSDE问题。 2.BSDE深度模型。 (21) 包含所有N-1个子神经网络的架构如图1所示。 图1 深度BSDE模型结构 回到偏微分方程求解的核心问题,不难发现,经过神经网络的多次训练迭代,随着损失函数值的下降并趋于稳定,神经网络中的参数也逐渐趋于稳定,将最终的参数θu0输出,就可以得到问题的近似数值解。 3.一个高维PDE问题。 为了说明该法的泛用性以及在高维场景的高效性,本节首先将该方法应用于如下一个在100维空间中(d=100)的典型的Allen-Cahn方程: (22) (23) 数值实践上,本文主要利用Python中的PyTorch机器学习库,搭建神经网络模型进行求解。训练数据集和测试数据集分别为256组和64组随机生成的几何布朗运动路径,每一个子网络设计3个隐藏层,每一层的神经元设为d+10,每经过一层网络,先进行批标准化(Batch Normalization),随后经激活函数线性整流函数(Re-LU)进入下一层。整体后向传播中,优化函数选取Adam算法。Adam 是一种可以替代传统SGD过程的一阶优化算法,它能基于训练数据迭代地更新神经网络权重。迭代过程持续4 000次,并每隔100次训练,便在验证集上进行结果验证,损失函数和目标函数值随迭代次数变化情况如图2所示。可以看到,随着迭代次数的增加,损失函数值趋近于0.003 4,数值解的值趋近于0.052 4±0.000 726,与其他数值方法所得解一致。整个运算过程耗时528秒。 图2 损失函数值与数值解估计值变化 为了分析网络参数的影响,我们设置了不同隐藏层,并记录了模型达到不同损失函数值对应的耗时,需要注意的是,本文所提到的耗时是实验用机器配置的结果,仅具有相对意义。图3给出了不同隐藏层达到不同损失函数值所需要的计算时间,计算时间是计算32次的平均结果。调整神经元数量获得的结果类似。从图3可以看到,隐藏层数量增加以及神经元数量增加大幅度增加了计算时间。尽管通用逼近定理表明不同隐藏层和神经元数量都可以达到同样效果,但一般来说,设置为3隐藏层以及d+10个神经元能够满足需求,也是多次实际求解后的经验总结。 图3 不同网络参数对应的损失函数值-耗时的关系图 由上一部分的结果可知,深度BSDE模型可以较为准确地给出偏微分方程的数值解。这一部分将对模型的参数进行分析,并提出一些改进的思路。 表1 不同组别中参数θu0初始值取值范围 在图4中,U[yl,yr]中对参数θu0进行采样得到的初始化的点约为0.083,这使得参数值在第200步迭代时就几乎达到正确解,说明其以很快的收敛速度到达正确解附近;而在图5中,参数初始化的点更大,导致参数值收敛速度较U[yl,yr]=[0.06,0.1]情况下更慢,在第2 400步迭代时,才收敛至正确解附近;在图2中,参数值的收敛速度则介于两个实验组之间。此外,在三组实验中,模型总耗时并无较大差别。 图4 [yl,yr]=[0.06,0.1]下的数值解估计值变化 图5 [yl,yr]=[0.6,1]下的数值解估计值变化 表2 不同组别中参数θu0初始值取值范围 图6 参数θu0从U[-0.01,0.01]中采样的结果 图7 参数θu0从U[0.1,0.3]中采样的结果 2.子神经网络输出值的调整。 在深度BSDE模型中,将时间区间[0,T]离散化后,在除0时刻与T时刻外的每一个时间点,以该时间点下的资产价格为输入,得到目标函数在这一点的梯度值,并代入迭代式中,最终得到目标函数在T时刻的值。之前本文已经给出了通过离散化后的BSDE得到的资产价格以及目标函数的过程迭代式,现将其重新写在下方。 Xtk+1-Xtk≈μ(tk,Xtk)Δtk+σ(tk,Xtk) (24) ΔBku(tk+1,Xtk+1)-u(tk,Xtk) (25) 3.布朗运动生成模型调整。 在构建模型之前,参考蒙特卡洛模拟的过程,需要借助漂移项μ与波动项σ对资产价格按几何布朗运动进行模拟。在第二章的模型搭建中,本文直接借助Python中scipy工具包提供的相关函数生成了标准正态分布随机数,进而拟合标准布朗运动,从而对资产价格进行了模拟。然而在蒙特卡洛模拟中,关于标准正态分布随机数的生成有多种不同的方法,按效率从低到高、效果从差到好,有拒绝采样、反函数法、Box-Muller法、ziggurat算法等。 在反函数法中,需要借助服从均匀分布U(0,1)的随机数,来生成符合标准正态分布的随机数。对于均匀分布随机数的生成,往往有现成的工具包可以调用。但实际上,常规随机数生成方法得到的随机数均为伪随机数,在低维场景下可能并不会暴露出弊端,而当来到高维场景下,这样的随机数往往不能较为完整地对高维空间进行覆盖,也就是不够“均匀”。用这样不够“均匀”的随机数去生成正态分布随机数,进而对高维布朗运动进行拟合,可能会降低模型预测的精确度。 对于这一类问题,蒙特卡罗模拟法中的一个思想是:用低差异序列代替均匀分布随机数,来对高维布朗运动进行拟合,这就是蒙特卡洛模拟法的一个变形——拟蒙特卡罗模拟法,该法由Joy等(1996)[16]首次应用于期权定价领域。所谓低差异序列,是一种依据数论知识,从概率分布中得到代表样本组成的序列,该序列具有更好的确定性和均匀性,且其在高维空间中仍能维持这一优点,故可以在处理篮子期权这类高维期权定价问题时选用低差异序列来进行数值模拟。常见的低差异序列包括Halton序列、Faure序列以及Sobol序列等,下面对Halton序列进行简要说明: 为了对高维情况下低差异序列的优势进行简单说明,本文基于均匀分布生成随机数与Halton序列,分别构造1 000个1 000维的随机点,并在第999维与第1 000维度组成的平面上进行投影,图8给出了均匀分布随机数(左)与低偏差序列(右)在高维度情况下的投影散点图。可以比较明显地看到,在高维度下,均匀分布随机数对空间的覆盖度远不如Halton序列。 图8 均匀分布随机数(左)与低偏差序列(右)在高维度情况下的投影散点图 总的来说,利用低差异序列与反函数法等算法生成高维标准正态分布随机数,进而对高维标准布朗运动进行模拟,可以作为BSDE深度模型的一个改进思路。 以下将深度BSDE模型应用于篮子期权的定价中,首先构造一个包含5个资产的高维问题场景,进行数值模拟,随后采用前面提到的改进思路,再分别进行模拟。最后,将用蒙特卡洛模拟法进行模拟,并将两种算法在均匀分布随机数与低差异序列两种设定下的结果进行对比,同时对深度BSDE模型是否具有更高的时间效率这一问题进行验证。 1.深度BSDE模型定价数值结果。 首先给出篮子期权的BS模型: 对照深度BSDE模型的通式,得到如下的对应关系: μ(t,S(t))=(rS1(t),rS2(t),…,rSd(t))T f=-rV 其中: S(t)=(S1(t),S2(t),…,Sd(t)) 且ΛΛT=Σ。 随后对问题所涉及的数据进行设定,5个标的资产的初始价格分别为50、46、51、48以及55,波动率分别为0.1、0.2、0.16、0.22、0.18,协方差矩阵∑为: 篮子内每个资产的权重ωi=1/d=0.2,交割价格K=50,无风险利率r=0.08,时间区间设定为[0,1],并将其分解为8份。 数值实践上,仍然利用Python中的Pytorch机器学习库,搭建神经网络模型进行求解。训练数据集和测试数据集分别为256组和64组随机生成的几何布朗运动路径,每一个子网络设计3个隐藏层,每一层的神经元数目设为d+10=15,每经过一层网络,先进行批标准化(Batch Normalization),随后经激活函数线性整流函数(ReLU)进入下一层。整体后向传播中,优化函数选取Adam算法。迭代过程持续6 000次,依旧每隔100次训练,便在验证集上进行结果验证,主要观察损失函数和收敛值的变化,给出输出结果以及损失函数随迭代次数变化情况如图9和图10所示。从图中可以看到,随着迭代次数的增加,损失函数值趋近于4.035 5,数值解的值趋近于7.929 4±0.025 148,整个运算过程耗时1 243秒。 图9 常规BSDE模型损失函数值变化 图10 常规BSDE模型数值解估计值变化 2.更改神经网络输出值。 图11 更改神经网络输出值的BSDE模型损失函数值变化 图12 更改神经网络输出值的BSDE模型数值解估计值变化 对比更改神经网络输出值前后的数值解拟合情况(图13、图14),发现这样的改动并未对其产生过多影响,但却大大提高了模型训练的速度,时间缩短了4.5倍,实验结果验证了前文提出的猜想。 图13 更改神经网络输出值前后的BSDE模型数值解拟合情况对比 图14 更改神经网络输出值前后的模型训练时间长度对比 3.Halton序列模拟资产价格运动。 基于Halton序列,借助反函数法生成标准正态分布随机数,进而模拟资产价格的几何布朗运动,依照此思路对初始的常规BSDE模型进行改进。在神经元数等超参数、优化函数的选取、迭代次数的设置等均不变的情况下,每隔100次训练,便在验证集上进行结果验证,给出输出结果以及损失函数随迭代次数变化情况如图15、图16所示。 图15 Halton序列的BSDE模型损失函数值变化 图16 Halton序列的BSDE模型数值解估计值变化 从图17可以看到,随着迭代次数的增加,损失函数值趋近于3.687 5,数值解的值趋近于7.793 0±0.016。可见,一方面,损失函数最终趋于稳定后的值较常规BSDE模型略低;另一方面,数值解的估计值较常规BSDE模型略低,但波动更小。这说明,在d=5的情况下,低差异序列的确可以得到更加稳定的定价结果。 图17 选用Halton序列生成随机数前后的BSDE模型数值解拟合情况对比(趋于稳定后) 4.蒙特卡洛模拟。 为了说明BSDE深度模型的优越性,在这里本文使用蒙特卡洛模拟对篮子期权进行定价,并与BSDE深度模型进行对比。 篮子期权中的每个标的资产满足式(26)随机微分方程。将时间区间[0,T]等分为n份,有0=t0 dSi(t)=μiSi(t)dt+Si(t)ΛidB(t) (26) 令Gi=G(t,Si)=lnSi,根据伊藤引理,Gi也是伊藤过程,则有如下伊藤公式: (27) 为了便于进行蒙特卡洛模拟,这里将标准布朗运动进行了展开,其中Zj~N(0,1)。将Gi=G(t,Si)=lnSi代入式(27),并在方程两边对t在(tk,tk+1)上积分,有: (28) 经过整理得到: (29) 本文以式(29)作为依据进行蒙特卡洛模拟,分别选用均匀分布和Halton序列,使用反函数法进行随机数的生成(选取Halton序列进行随机数的生成时的蒙特卡洛法常被称作拟蒙特卡罗模拟法)。这里同样将时间区间[0,1]划分为8等份,与深度BSDE做同样处理。经过20 000次模拟,当选用均匀分布进行随机数生成时,估计值为7.911 4,标准差高达11上下;当选用Halton序列进行随机数生成时,估计值为7.884 2,标准差为9上下。可见,在数值估计的结果上,深度BSDE模型与蒙特卡洛数值模拟得到的结果相近,却更稳定(图18)。 图18 两种模型在不同情况下的估计值对比 本文将传统BS模型置于高维情境下,自然地引入高维期权定价的典型模型、篮子期权定价的BS模型,并详细指出高维情境下BS模型存在的问题:如篮子期权不同于一维情况下的BS模型,需要考虑期权中每个资产价格变化路径之间的相关性;且虽然篮子期权价值取决于所有资产的价格算术平均加权,但加权之后的价值变动不再满足几何布朗运动定义,无法套用一维情况的BS定价公式对其进行定价,更难以像一维期权那样绕开偏微分方程的求解问题。基于这些问题,本文利用BSDE的解与偏微分方程的解之间存在唯一对应关系的事实,引出借助离散BSDE迭代式来对问题进行求解的思路;随后本文引入神经网络,解决了迭代式目标函数梯度值不可得的问题,同时将期权价格作为神经网络的参数参与到整个网络训练中,并利用终值条件构造损失函数,在模型训练结束的同时得到神经网络参数的期权价格,从而完成问题求解。 接下来本文应用上述深度BSDE模型对篮子期权定价问题进行求解,同时利用实证结果证明该算法具备一定的精度,以及较高的求解效率:一方面,本文从初始参数设置、子神经网络输出值调整,以及随机数生成三个方向,提出已有模型的改进思路,且在计算以包含5个无分红资产的资产组合为标的资产的篮子期权价格的实证中加以验证,表明这三个方向确实能够提高计算效率;另一方面,本文将基于深度BSDE模型的数值结果与蒙特卡洛模拟结果进行对照,验证了前者的有效性以及一定的精度。 本文研究还表明,深度BSDE模型除了可以解决基本假设下的篮子期权定价问题,还可以对其他假设下的,如带跳扩散过程、随机波动率、分数布朗运动环境下等的篮子期权定价问题进行求解,具有在更广范围使用的潜力。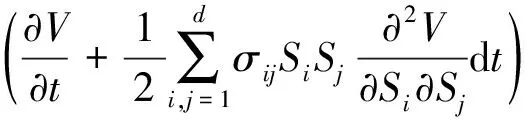
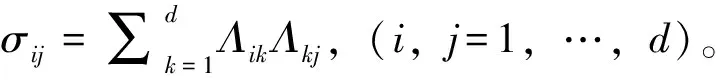
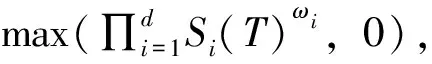
(二)BSDE介绍




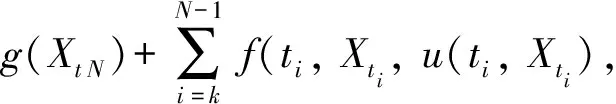










三、模型分析与数值实践
(一)模型分析与改进


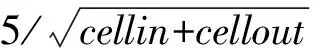














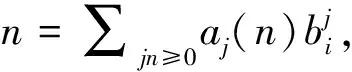

(二)篮子期权定价









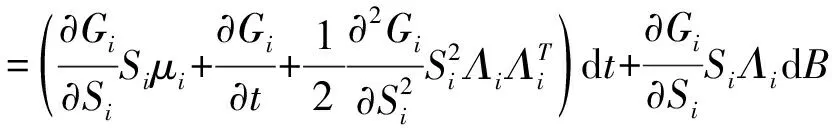

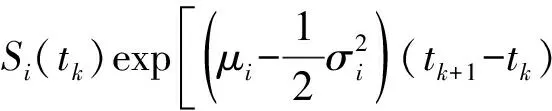

四、结论

