延迟退休、隔代照料与生育率
张世伟 王 杰
一、引言
长期的人口低增长和预期寿命延长,使得中国社会老龄化程度不断加深。据《第七次全国人口普查公报(第五号)》显示,中国60岁和65岁以上人口占总人口比重分别约为18.7%和13.5%,远高于联合国提出的老龄化社会标准,“未富先老”已成为中国经济持续稳定增长的巨大挑战。一方面,人口老龄化会导致有效劳动供给不足(李建伟,2020[1];刘骏等,2021[2]),促使企业用工成本增加;另一方面,预期寿命大幅延长,而法定退休年龄仍处于较低水平,将会导致养老保障体系超负荷运行(张苏和李泊宁,2021[3];林宝,2021[4])。
借鉴发达国家的经验,延迟退休已成为积极应对人口老龄化问题的一个必要措施。中国现行的法定退休年龄仍沿袭了20世纪70年代末的标准(1)根据《国务院关于安置老弱病残干部的暂行办法》和《国务院关于工人退休、退职的暂行办法》(国发【1978】104号)的规定,中国职工现行退休年龄是,男性60周岁,女干部55周岁,女工人50周岁。,但随着中国经济的持续增长和人民生活水平的不断提高,人口预期寿命不断延长,而法定退休年龄却一直未发生根本性变动(2)为充分发挥骨干专业技术人员和女性干部的作用,中国相关部门相继颁布《国务院关于延长部分骨干教师、医生、科技人员退休年龄的通知》《中央组织部人力资源社会保障部关于机关事业单位县处级女干部和具有高级职称的女性专业技术人员退休年龄问题的通知 》等文件,延迟相应人群的退休时间。。法定退休年龄过低,不仅会加大养老金支付缺口,而且会导致人力资源的闲置和浪费(朱华雄和阳甜,2020[5])。因此,延长法定退休年龄就显得势在必行。
欲研究延迟退休对生育率的影响,中国社会的两个典型特点值得关注:首先,中国传统家庭存在着隔代照料文化,即老年人帮助子女照料孙辈。据北京大学社会科学调查中心的中国家庭追踪调查(China Family Panel Studies,CFPS)2018年数据显示,孩子白天由(外)祖父母照料的比例为30.65%,晚上由(外)祖父母照料的比例为25.78%,老年人帮助年轻人照料孩子可以放松年轻人照料孩子的时间约束,促使其提高生育意愿。然而,延迟退休则对这一部分家庭劳动时间存在挤出效应,进而对年轻人的生育率产生负向影响。其次,中国传统家庭文化存在“养儿防老”观念。孩子作为一种投资品,可以降低个体老年期的不确定性,而延迟退休作为一种家庭养老的替代,将降低对子女养老的需求,导致生育率随之降低。一些研究表明,在实施渐进式延迟退休政策过程中,人均预期寿命的延长也会导致生育率降低(Zhang和Zhang,2005[6];Soares,2005[7];Chen,2008[8];Cervellati和Sunde,2014[9])。
然而,延迟退休导致个体老年期的闲暇期缩短,而工作期延长。根据经济学理论,理性行为人会降低预防性储蓄,年轻时的可支配收入增加,可能会提高生育意愿。此外,工作期的延长导致预期的终生收入增加。如果个体收入均用于消费、储蓄和生育,则在孩子是正常消费品的情形下,理性行为人会增加对孩子的需求,进而导致生育率提升。
目前,国内文献大多通过构建内生生育率的世代交叠模型来研究延迟退休对生育率的影响,但研究结论却不尽相同。一些学者认为,生育率随着退休年龄的延长而降低,主要缘于退休年龄的延长,不仅降低了老年人对家庭代际养老的需求(郭凯明和颜色,2016[10];王丽莉和乔雪,2018[11]),而且挤出了老年人隔代照料的时间(周鹏,2017[12];郭凯明等,2021a[13];郭凯明等,2021b[14])。封进和韩旭(2017)[15]、封进等(2020)[16]的研究发现,已经办理退休手续或超过法定退休年龄的老年人会显著增加隔代照料时间,其子女的生育水平相对较高,而延迟退休则会显著降低老年人参与隔代照料的时间。
另一些学者认为,延迟退休会对生育率产生积极影响。严成樑(2016)[17]、于文广等(2021)[18]认为延迟退休通过两种途径影响生育率:一方面使得老年期收入增加,个体减少成年期的储蓄和工作时间,生育孩子的时间禀赋提高;另一方面使得资本存量减少,工资水平下降,个体为实现效用最大化而延长工作时间,生育孩子的时间禀赋减少。尽管两者对生育率产生了相反方向的影响,但收入增加的正向效应占主导作用。此外,杨华磊等(2018)[19]基于OECD国家的数据研究发现,延迟退休促使生育水平提升,主要缘于延迟退休创造的产出增加了社会可用的生育资源,通过再分配政策(如生育补贴等),促进了家庭生育水平的提高。但严成樑(2018)[20]认为,延迟退休对生育率的影响是不确定的,在世代交叠模型的不同参数设定下,生育率与延迟退休之间呈单调递减或倒U型变动趋势。
综上所述,从长期均衡的角度来看,延迟退休对生育率既有积极影响也有消极影响,最终影响的方向取决于上述两种效应的相对大小。因此,本文拟在Wigger(1999)[21]、Miyazaki(2014)[22]和Cipriani(2013,2016)[23][24]模型的基础上,构建一个内生生育率和现收现付制(Pay-as-you-go,PAYG)社会养老保险制度的世代交叠模型,在模型中引入隔代照料、家庭养老和延迟退休,并应用数值模拟方法,分析在人口老龄化的背景下,延迟退休对隔代照料及生育率的影响。基于2018年CFPS数据,本文对理论假说进行实证检验。本文可能的贡献主要体现在两个方面:首先,将延迟退休、家庭养老和隔代照料引入世代交叠模型,通过理论分析,得出除增加终生收入、缩短隔代照料时间之外的延迟退休影响生育率的另一条途径——降低家庭赡养比率和老年个体的家庭养老需求,进而降低对孩子作为“投资品”的需求,导致生育率降低;其次,现有研究主要从理论上探究延迟退休对生育率的影响,本文基于CFPS数据的研究为理论假说提供了一个经验证据。
本文剩余部分的内容安排如下:第二部分构建理论模型;第三部分运用数值模拟的方法分析延迟退休对生育率的影响;第四部分基于CFPS数据实证分析父代延迟退休对子女生育意愿的影响;第五部分给出本文的结论和政策启示。
二、理论模型
在Wigger(1999)[21]、Miyazaki(2014)[22]和Cipriani(2013,2016)[23][24]模型的基础上,本文构建了一个包含内生生育率、隔代照料和延迟退休的世代交叠模型。假设经济是封闭的,由个体、企业和一个负责现收现付制社会养老保险的政府组成。
(一)个体
假设时间是离散的,t=0,1,2,3,…,个体一生分为三个时期:幼年期、成年期和老年期。在幼年期个体不采取任何行动,仅接受成年个体和老年个体的抚养。每个成年个体均有1单位的时间禀赋,在劳动供给和照料孩子之间分配,获得的劳动收入用于满足成年期的消费、储蓄以及向老年个体提供赡养费。老年个体的时间禀赋为T,用于劳动供给、隔代照料和享受闲暇,并消费当期劳动收入、成年期的储蓄及利息、子女提供的赡养费及养老保险金。
假设在t时期,有Nt个成年个体参加工作,生育率为nt=Nt+1/Nt,生育和照料一个孩子的时间和货币成本固定为υ(Zhang和Zhang,2005[6];严成樑,2018[20];于也雯和龚六堂,2021[25])。老年个体为每个子女提供的隔代照料时间均为Zt,并且老年个体和成年个体对孩子的抚养可以完全替代,则成年个体提供劳动供给的时间为1-υnt+Zt。给定单位有效劳动的工资率wt,则成年个体获得工资收入为:
(1)
成年个体的工资收入在缴纳养老保险费(对企业征收的养老保险费用均转嫁给个体(3)根据Summers(1989)[26]和Gruber(1997)[27]的研究,当劳动供给弹性越小、需求弹性越大时,企业转嫁工资税或社保缴费成本给员工的能力越强。假设个体劳动供给缺乏弹性,因此对企业征收的税费均转嫁给劳动者。)后,用于成年期消费、储蓄以及赡养老人。因此,成年个体的预算约束为:
(2)
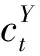

(3)
(4)
(5)
其中,β为主观贴现因子,即老年期消费形成的效用相当于成年期消费效用的贴现值;γ和ρ分别表示相较于成年期消费,个体对生育孩子和老年闲暇的重视程度。个体在式(1)~式(4)的约束下最大化终生效用函数(5),最优的成年期消费、储蓄、生育孩子数量及隔代照料决策满足如下关系:

(6)
(7)
(8)
(9)
(二)企业
在一个封闭的经济体中,所有的企业均生产同质产品。企业以利润最大化为目标,在完全竞争的市场环境中利用资本和劳动进行生产。假设产出采用Cobb-Douglas形式的生产函数,Kt和Lt分别表示t期使用的资本和劳动,并将全要素生产率标准化为1,则生产函数的形式为F(K,L)=KαL1-α,α∈(0,1)表示资本产出弹性,企业面临的利润函数为:
F(Kt,Lt)-RtKt-wtLt
(10)
其中,wt表示单位有效劳动的工资率。假设资本在一期内完全折旧,Rt=1+rt表示资本总收益率。在有延迟退休的情形下,有效劳动供给总量为Lt=Nt(1-υnt+Zt)+Nt-1x,单位有效劳动的产出和资本存量分别为:yt=Yt/Lt,kt=Kt/Lt。在完全竞争市场中,企业利润最大化的条件为:
(11)
(三)养老金财政收支平衡
借鉴Miyazaki(2014)[22]的设定,在现收现付制养老金的计发规则下,政府从当期工作的成年个体和老年个体工资中征收养老保险费,用于支付当期退休老年个体的养老金。假设政府养老保险的财政收支平衡,则有:
Nt(T-x)Pt+1=τwt+1(1-υnt+1+Zt+1)Nt+1+τwt+1xNt
(12)
处于t时期的成年期个体在t+1期可以取得的养老金数额为:
(13)
(四)经济均衡


(2)在生产要素价格变量(Rt,wt)给定前提下,企业选择生产要素(Kt,Lt)最大化利润。
(3)劳动力市场出清,成年个体和老年个体的劳动供给等于企业的劳动需求:
Lt=Nt(1-υnt+Zt)+Nt-1x
(14)
(4)资本市场出清。由于资本在当期末完全折旧,因此,企业t+1期初的资本存量完全来自t期成年个体的储蓄,资本市场的出清条件为:
Kt+1=stNt
(15)
单位有效劳动的资本存量为:
(16)
(5)养老保险收支平衡,方程(7)和(8)成立。初始的老年个体消费为:
(17)
(五)稳态方程
将个体成年期最优消费表达式(6)、养老金表达式(13)代入方程(9),可得:
(18)
(19)
由企业的利润最大化条件(11),得:

(20)
将方程(16)代入方程(20),并结合方程(6)、(7)和(13)可得:
(21)

(22)
Z=
(23)
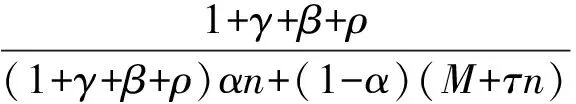
(24)
上述三个方程是关于稳态生育率n、利率R和隔代照料时间Z的非线性方程,据此可以求解得到n和R。由方程(22)可以考察延迟退休对隔代照料时间的影响:
(25)
由此可以看出,延迟退休将会挤出隔代照料的时间。进一步地,可得:
(26)
即当个体对老年期休闲偏好增加时,延迟退休对老年个体隔代照料时间的挤出效应更加凸显。
此外,据方程(22)还可以考察预期寿命延长对隔代照料时间及生育率的影响:
(27)
(28)
由方程(27)和(28)可知,预期寿命的延长,对稳态生育率和老年个体的隔代照料时间均具有正向的影响。
三、数值模拟和结果分析
由于模型稳态方程的表达形式过于复杂,无法求出解析解,进而无法应用简单的比较静态分析方法进行分析,因此本文采取数值模拟的方法探究延迟退休对隔代照料以及生育率的影响。结合现实经济中孩子由个体及其父辈共同照料的现象,本文假设老年个体的隔代照料时间Z为正;在减去老年个体隔代照料时间后,成年个体抚养孩子的时间为正,即υn-Z>0。
假设个体从21岁开始参加工作,成年期和老年期长度均为35年,并且个体都可以存活到老年期,老年个体的存活时间随着预期寿命的延长而增加。根据中国国家卫生健康委员会的调查,2019年中国人口的平均预期寿命为77.3岁,即T的取值约为0.64(22.3/35)。在没有延迟退休的情形下,正常的退休年龄为55岁,个体刚好在进入老年期时退休。假设法定退休年龄最多延迟至65岁,即x由0逐渐增加到0.3(10/35)。借鉴Fanti和Gori(2013)[30]、严成樑(2018)[20]、景鹏和郑伟(2020)[31]以及于也雯和龚六堂(2021)[25]等的研究,本文将参数的基准取值设定如表1所示。

表1 模型参数含义及基准取值

图1给出了在参数基准取值下,延迟退休的经济效应,其中横轴表示延长法定退休年龄的长度。可以发现,随着法定退休年龄长度的增加,稳态生育率、老年个体隔代照料的总时间和家庭赡养比率均降低,成年个体照料孩子的时间延长,储蓄率上升,而社会的劳动供给总量呈现出先上升后下降的倒U型变动趋势。这主要缘于随着退休年龄的延长,老年个体工作时间延长导致的劳动供给增加逐渐被生育率降低导致的劳动供给减少所抵消。在模型参数的基准取值设定下,存在使总劳动供给最大化的延迟退休年龄,约为7年(x=0.21),此时的退休年龄约为62岁。
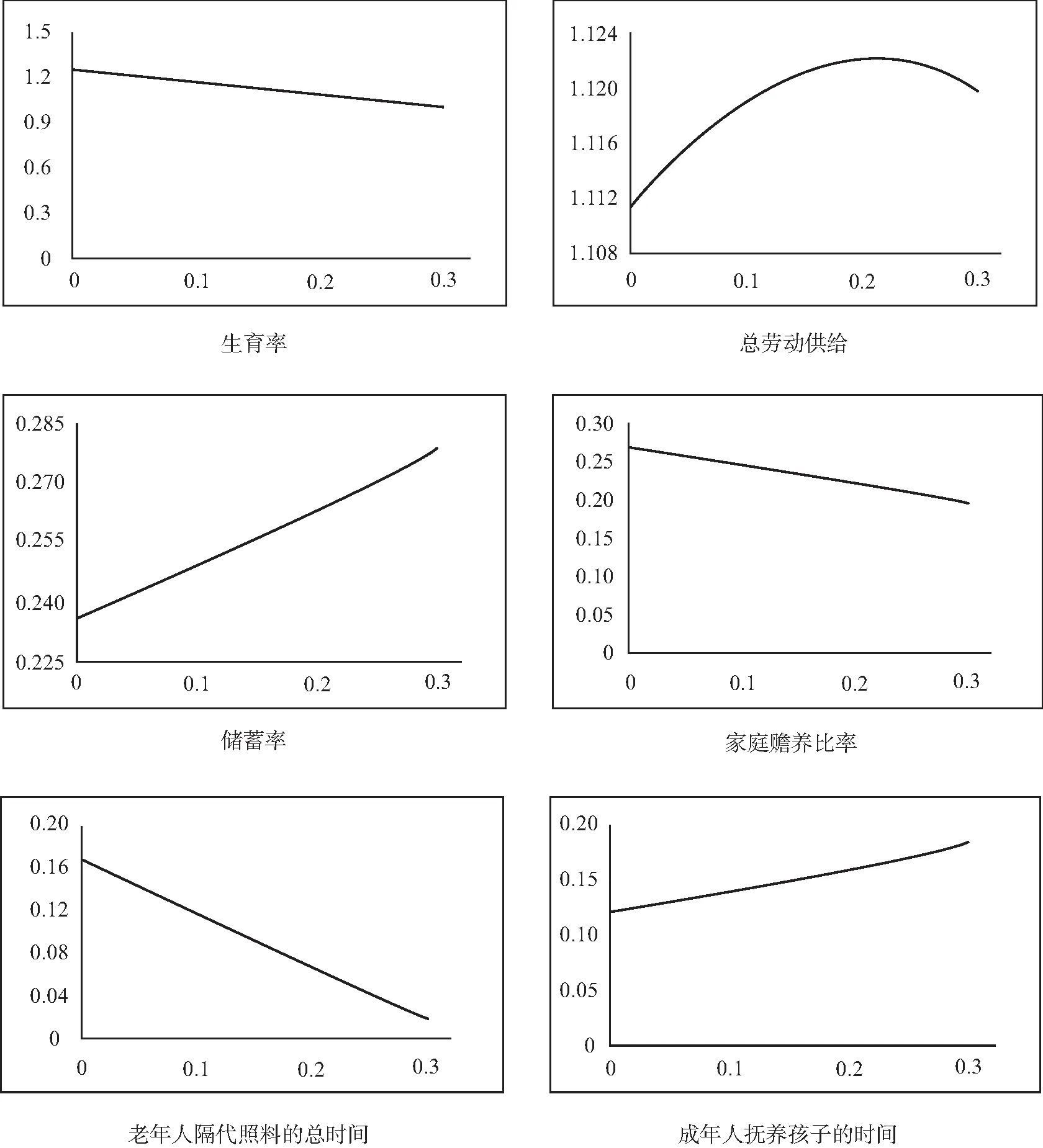
图1 延迟退休对经济的影响
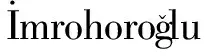
另一方面,延迟退休可以增加个体老年期的收入,使得个体在老年期的不确定性降低,从而降低了家庭养老的需求,因此降低了对孩子作为投资品的需求,导致生育率也随之降低。这一点由家庭赡养比率随退休年龄的延长而降低可以看出。因此,即使延迟退休导致个体在成年期照料孩子的时间增加,其对生育率的微弱正向效应也将被抵消,最终表现为延迟退休降低了生育率。
延迟退休对隔代照料时间和生育率的影响可能会与模型参数的选取有关。为此,本文假设参数在合理的取值范围内变动,以考察参数取值变化对数值模拟结果的稳健性。假设贴现因子、老年期闲暇偏好、照料一个孩子的时间成本和成年个体提供的义务赡养份额在基准值附近变动,分别取β为0.6和0.8,ρ为0.3和0.5,υ为0.15和0.25,M为0.1和0.2。与前文一致,在基准生育率1.3和没有延迟退休的情形下校准γ,据此考察延迟退休对隔代照料时间和生育率影响的稳健性。
表2给出了延迟退休对隔代照料和生育率影响的稳健性检验结果。可以发现,相关参数在合理取值范围内变动时,生育率和隔代照料时间依然会随着退休年龄的延长而降低,这与参数基准取值的模拟结果是一致的,说明本文的数值模拟结果具有稳健性。此外,随着个体对老年期消费和闲暇偏好的增加,老年个体提供的隔代照料时间将减少,生育率也随之降低;随着生育和照料一个孩子的时间成本的提高,老年个体的隔代照料时间将有所增加;随着成年个体对老年个体义务赡养费用的降低,老年个体提供的隔代照料时间减少,但生育率将有所提升,这是由于成年个体义务赡养费用的降低放松了成年期的预算约束,导致对作为消费品属性的孩子数量的增加。

表2 延迟退休对隔代照料和生育率影响的稳健性检验
随着经济发展和医疗卫生条件的改善,人均预期寿命将日益延长。基于这一思想,本文进一步将老年期长度逐渐增加至0.85(约为85岁),以探究在预期寿命延长情景下,延迟退休对生育率的影响(模拟结果参见表3)。在相同延迟退休长度下,生育率随着预期寿命的延长而增加,这主要缘于预期寿命延长使得老年个体有更多的时间禀赋,用于隔代照料的时间亦随之增加,进而放松成年个体照料孩子的时间约束,导致生育率的提高。

表3 预期寿命延长对生育率的影响
综合前文的理论分析与数值模拟结果,本文得出如下的理论假说:延迟退休不仅导致家庭赡养比率的降低,而且挤出了老年个体的隔代照料时间,二者对生育率的负向影响大于成年个体照料孩子时间增加对生育率的正向影响,最终表现为延迟退休将导致生育率的降低。
四、基于CFPS数据的实证检验
(一)数据、变量和模型
前文理论分析的结果表明,延迟退休会导致长期均衡生育水平的降低。由于短期内无法观测到延迟退休对自身生育水平的影响,因此本文拟基于2018年CFPS数据,实证检验父代延迟退休对子女生育意愿的影响。
依据已有研究(李勇辉等,2021[37])的经验和中国的法定结婚年龄(男性22周岁,女性20周岁),本文将研究样本的年龄限定为男性22~50周岁,女性20~50周岁。首先,通过家庭数据库识别出个体的父亲和母亲,获取父母的个体特征变量。其次,通过家庭编码匹配家庭经济信息数据库,获取家庭收入和房产信息。再次,通过父母的编码在成年个体数据库中匹配父代个体,识别父代个体是否延迟退休、隔代照料情况以及与子女之间的经济联系。最后,删去年龄超过70岁的父代个体。为了避免异常值的影响,删去了期望生育孩子个数大于4的57个个体,并对收入类连续变量进行前后1%的缩尾处理。最终数据得到的子女个体数量为2 600个,其中父代个体选择延迟退休和不延迟退休的分别有338个和2 262个。
本文的被解释变量为成年子女的生育意愿,根据问题“您认为自己有几个孩子比较理想?”的回答设置生育意愿变量。此外,本文通过家庭数据库识别出个体实际已生育的孩子个数,作为被解释变量的替代变量。依据问卷中询问的问题“是否帮助子女照料孩子或料理家务”“料理家务的频率”以及父代与子女之间的经济联系设置隔代照料和经济交换的相关变量。
本文的核心解释变量为父代个体是否延迟退休,CFPS问卷中询问了个体是否退休及就业形式,如果父代个体超过法定退休年龄(男性60周岁,女干部55周岁,女工人50周岁)且仍在正规就业(有编制或与雇主签订劳动合同),则定义为延迟退休。如果父代个体已办理了退休手续或正在领取退休金(或养老金),则定义为非延迟退休。
为探究父代个体延迟退休对子女生育意愿的影响,本文将生育意愿决策方程设定为如下形式:
yij=β0+β1delayij+γXij+λDj+εij
(29)
其中,下标i和j分别表示个体和省份;y表示个体的生育意愿;delay表示父亲或母亲是否延迟退休;X表示影响个体生育意愿决策的其他控制变量,依据已有研究的经验,本文控制了个体特征(年龄、性别、受教育年限、婚姻状况、健康状况、就业状况等)和家庭特征(自有房产数目);D表示省份特征,包括人均GDP、生育保险支出额和地区平均房价等;ε表示随机误差项。
表4给出了父亲或母亲是否延迟退休与子女生育意愿、父母隔代照料情况以及其和子女间经济交换的统计描述(6)T检验的结果表明,“父母至少一个延迟退休”一列两组均值具有显著性差异的变量为:生育意愿、已生育孩子数、父母给子女的经济支持和父母给子女的经济支持净额;“父亲延迟退休”一列两组具有显著性差异的变量为:父母受教育年限和父母年收入;“母亲延迟退休”一列两组变量均具有显著性差异。限于篇幅,T检验的结果未给出,感兴趣的读者可以联系作者索取(同表5)。。可以发现,与未延迟退休相比,选择延迟退休的父代个体受教育年限和年收入水平较高。这说明受教育水平较高的父代个体,从事脑力劳动和管理工作的占比更大,更倾向于选择继续工作,其年收入也随之增加,而受教育水平较低的父代个体,因其可能从事更多体力劳动而选择在达到退休标准后退出劳动力市场。与父代个体未延迟退休的情形相比,无论父亲延迟退休还是母亲延迟退休均会导致子女生育意愿的降低。延迟退休不仅会导致母亲参与隔代照料概率的降低,还会导致其提供的隔代照料时间的缩短。而这一数值在父亲是否延迟退休的选择中恰恰相反,也即延迟退休的父亲,提供隔代照料的概率和时间均大于未延迟退休的情形。此外,延迟退休的父代个体给子女的经济支持净额大于未延迟退休的父代个体,因此可能存在父代对子女生育的“时间-金钱”支持的平衡机制。如果父代个体选择延迟退休,则子女对其向上的经济支持会有所降低,说明延迟退休作为一种自我养老方式,可能会缓解子女的养老压力。
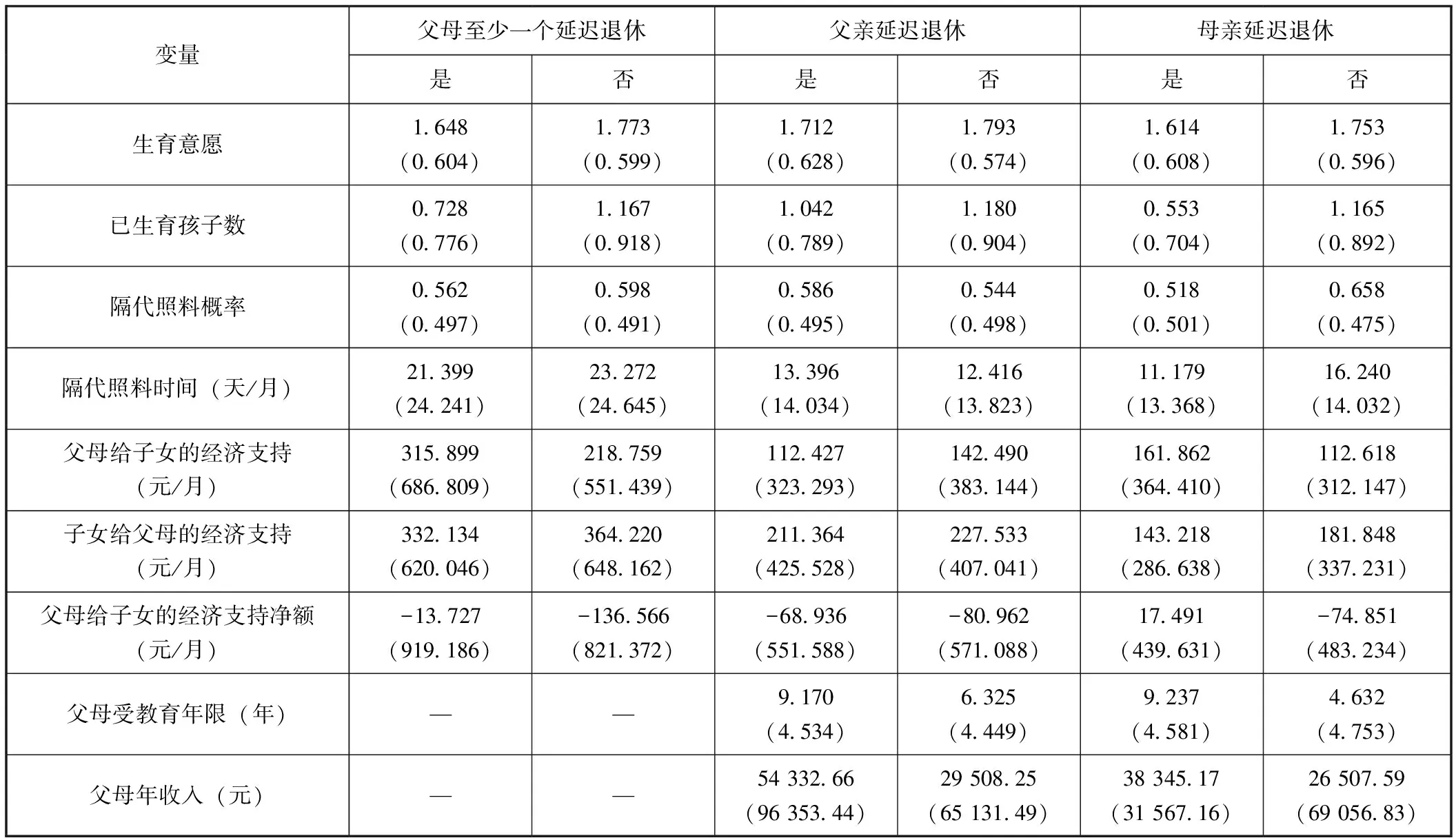
表4 父代延迟退休、隔代照料、经济交换与子女生育意愿的统计描述

表5 父代延迟退休与子女个体特征、地区特征
个体的生育意愿不仅取决于父代个体是否延迟退休,还与其个体特征及地区经济因素等有密切的联系。表5给出了父代延迟退休与子女个体特征及地区特征的统计描述(7)T检验的结果表明,“父母至少一个退休”一列除个体健康和房产数目外,其余变量的两组均值均具有显著性差异;“父亲延迟退休”一列,除受教育年限、农业户口、党员、房产数目和地区经济特征外,两组其余个体特征变量不具有显著性差异;“母亲延迟退休”一列,除健康和房产数目外,其余变量两组均值均具有显著性差异。。可以看出,父代延迟退休的家庭中,个体的平均年龄较低,男性和农业户口的比例较低,党员身份的比例较高,平均受教育年限较高,且个人经济状况较好,年收入和家庭自有住房数目较高。地区经济变量方面,父代延迟退休的个体所在地区的经济发展水平和房价水平较高,这表明在就业形势较好和家庭经济压力较大的地区,父代延迟退休的可能性更高。由于父代延迟退休和未延迟退休群体的个体特征和区域经济特征存在差异,需要应用回归调整方法才能准确度量延迟退休对子女生育意愿的作用效果。
(二)回归结果分析
1.基准回归结果。
表6给出了生育意愿决策方程(29)的回归结果。可以发现,母亲延迟退休对子女生育意愿的系数显著为负,父亲延迟退休对子女生育意愿的系数不显著,说明母亲延迟退休导致子女的生育意愿显著降低,而父亲延迟退休未对子女的生育意愿产生显著的影响。在不考虑内生性的情况下,母亲延迟退休导致子女生育意愿平均减少约0.04个。

表6 子女生育意愿决策方程的回归结果
个体和家庭控制变量方面,随着年龄的增长,个体的生育意愿先升后降,呈微弱的倒U型趋势;男性个体的生育意愿高于女性;已婚、农村户籍和党员身份的个体有更高的生育意愿;上周就业的个体生育意愿更低,说明正在工作的个体受时间的约束或害怕丢失工作而降低生育意愿;随着个体年收入水平的提高,生育意愿会提高,这说明收入效应在发挥作用,收入提升导致作为“消费品”属性的孩子数量的增加;家庭自有房产数的增加会导致生育意愿的提升。地区经济变量方面,经济发展水平高的地区平均生育意愿更低,这可能是由于经济发展水平更高的地区有相对较高的育儿成本;地区生育保险支出越高,说明地区的生育保障设施更为完善,平均生育意愿更高;作为生活成本的重要组成部分,地区平均房价的提升会显著抑制个体的生育意愿。控制变量的回归结果基本符合理论预期,说明生育意愿决策方程设定基本合理。
2.稳健性检验。
(1)负二项回归。
考虑到被解释变量生育意愿为非负的整数,使用经典线性模型的设定可能会降低估计效率,因此本文采用更适用于计数数据的泊松回归或负二项回归方法进行稳健性检验。泊松回归假定因变量服从泊松分布,要求样本的期望值等于方差,而现实经济数据往往不满足这一条件,使用负二项回归可以放松这一假定。通过观察数据(8)由于只有母亲延迟退休会对子女生育意愿产生显著影响,因此本文在稳健性检验和异质性分析中只保留了这一部分样本。可以发现,个体生育意愿的均值(1.736)大于样本方差(0.359),因此本文采取负二项回归模型更为合适。
表7列(1)给出了使用负二项回归模型对生育意愿决策方程的估计结果。可以看出,负二项回归模型回归系数的方向和显著性大致与表6第三列回归中的线性回归模型结果相一致,说明母亲延迟退休会对子女的生育决策产生显著的负向影响,导致子女的平均生育意愿减少0.05个。这也证明本文基准回归的结果是稳健的。

表7 稳健性检验
(2)更换被解释变量。
一般而言,个体的实际生育水平与生育意愿存在显著的正相关关系,基于此,本文以实际生育的孩子个数代替个体生育意愿作为被解释变量,探究母亲延迟退休对子女实际生育孩子个数的影响,回归结果如表7列(2)所示。可以看出,无论是OLS模型还是负二项回归模型,母亲延迟退休对子女实际生育孩子个数的系数均显著为负,说明母亲延迟退休导致子女实际生育水平显著降低。
(3)工具变量法。
为了避免遗漏变量带来的内生性问题,本文在基准回归中尽可能地加入影响生育意愿的控制变量。此外,考虑到母亲是否延迟退休与子女生育意愿之间可能存在双向因果关系,直接进行参数估计会导致偏误。因此,本文参照尹志超和张诚(2019)[38]以及顾和军等(2022)[39]的研究,构造同一社区父代个体的平均延迟退休率作为工具变量。一方面,同一社区的经济环境和政策环境大致相同,且因为“同伴效应”和“攀比效应”,父代个体选择延迟退休易受到社区中其他同代人的影响,满足工具变量的相关性条件;另一方面,一个社区的父代个体平均延迟退休率不会直接对子女的生育意愿产生影响,满足工具变量的外生性条件。因此,以同一社区父代个体的平均延迟退休率作为工具变量是合理的。
应用两阶段最小二乘法进行工具变量的参数估计。由于只有一个工具变量和内生解释变量,因此模型是恰好识别的。弱工具变量检验的Wald-F统计量值为151.86,在1%的水平上显著拒绝工具变量是弱工具变量的原假设。从表7列(3)的结果可以看出,在第一阶段中,社区平均延迟退休率对母亲延迟退休的系数显著为正,说明同一社区的同代人平均延迟退休率的提升显著促进了母亲的延迟退休。对比第二阶段与前文的回归结果,可以发现,在控制内生性后,母亲延迟退休对子女生育意愿仍有显著的负向影响,且这一数值较前文回归结果更大,说明基准回归结果具有稳健性。
(4)处理效应模型。
考虑到母亲延迟退休的选择可能是非随机的,也即子女生育意愿较高时,母亲选择延迟退休的概率也较低,因此直接进行因果推断可能会出现母亲延迟退休会导致子女生育意愿降低的结论。这与前文提及的双向因果造成的内生性问题是相似的。一个可行的方法是采用处理效应模型,将处理变量和结果变量的两个方程联合估计,以获得更准确的估计结果。具体操作为:第一阶段以母亲延迟退休作为被解释变量,以前文的工具变量和影响母亲延迟退休选择的其他个体或地区变量为自变量进行Probit回归,计算拟合值和逆米尔斯比。第二阶段,以生育意愿为被解释变量,以该拟合值、逆米尔斯比以及基准回归中的控制变量为自变量进行线性回归。
表7列(4)给出了使用处理效应模型对参数进行极大似然估计的结果。可以看出,逆米尔斯比的回归系数显著不为0,且Wald统计量在1%的水平上显著,说明母亲延迟退休是内生的解释变量,使用处理效应模型进行参数估计是合理的。第一阶段的回归结果汇报了Probit模型的系数,平均延迟退休率的系数为正,说明母亲易受同社区的“同伴效应”影响而选择延迟退休。第二阶段母亲延迟退休对子女生育意愿的影响显著为负,说明基准回归结果是稳健的。
(三)进一步分析
1.影响机制讨论。
理论模型的结论显示,父代延迟退休导致子女生育意愿降低的主要路径是挤出了其对孙子女的隔代照料时间。且通过数据的统计描述可以发现,父代对子女生育支持可能存在一种“时间-金钱”的平衡,即延迟退休虽然导致父代提供的隔代照料时间减少,但却增加了父代对子女的经济支持净额。为检验这一影响机制,本文将父代隔代照料决策、父代与子女之间的经济交换方程设定如下:
zij=θ0+θ1delayij+χQij+uij
(30)
其中,z为被解释变量,分别表示父代个体的隔代照料选择、隔代照料时间、子女给父代的经济支持、父代给子女的经济支持以及父代给子女的经济支持净额,当被解释变量为父代隔代照料选择时,方程为Probit形式。Q表示一系列控制变量,u表示随机误差项。
表8给出了母亲是否延迟退休与隔代照料决策以及经济交换的回归结果。可以发现,延迟退休不但会导致母亲参与隔代照料的概率显著降低10.11%,而且会挤出母亲提供隔代照料的时间(平均每月2.69天),进而导致子女的时间禀赋更为紧俏,生育意愿降低。此外,作为一种自我养老的方式,延迟退休导致子女给母亲的经济支持显著减少,家庭赡养比率降低。但延迟退休对母亲给子女的经济支持的影响不显著,且母亲因延迟退休而增加的向子女提供的经济支持净额对子女生育意愿的正向影响,未能弥补挤出的隔代照料时间对子女生育意愿的负向影响,因此生育意愿降低。

表8 母亲延迟退休与隔代照料、经济交换
表9给出了父亲是否延迟退休与隔代照料决策以及经济交换的回归结果。与母亲延迟退休相比,父亲延迟退休未对其隔代照料决策及其与子女之间的经济交换产生显著的影响,因而父亲是否延迟退休对子女的生育意愿也没有显著的影响。

表9 父亲延迟退休与隔代照料、经济交换
此外,考虑到中国典型的家庭特征,在一个家庭中,子女与父亲和母亲之间的经济交换通常是不可分割清晰的,因此本文从家庭的角度出发,探究父母至少有一个延迟退休对父母提供的总隔代照料时间以及经济支持净额的影响,结果如表10所示。可以看出,延迟退休导致父母提供的总隔代照料时间显著减少,而对经济支持净额的影响虽为正但不显著。因此,从家庭角度来看,延迟退休挤出的隔代照料时间也未被父母给予的经济支持所弥补,最终导致子女生育意愿降低。

表10 从家庭角度看隔代照料时间与经济支持净额
2.异质性分析。
前文的分析表明,母亲延迟退休导致隔代照料时间的挤出,进而导致子女生育意愿降低。而不同的个体面临着不同的生育成本,对隔代照料的需求也不尽相同,因此母亲延迟退休对不同个体生育意愿的影响也会有差异。基于此,本文依据性别、是否已有生育行为、是否就业以及个人年收入将样本划分为不同的子样本,探究母亲延迟退休对不同个体生育意愿的影响(9)由于2018年数据未调查社区信息,本文将2014年CFPS数据依据所居住社区是否有幼儿园等托幼机构,划分为两个子样本,结果显示母亲延迟退休对所居住社区没有托幼机构的子女生育意愿造成显著的负向影响。。
表11给出了异质性分析的回归结果。分性别来看,母亲延迟退休对女儿的生育意愿有显著的负向影响,而对儿子生育意愿的影响不显著。这可能是由于,相较于男性而言,生育行为对女性造成的压力更大,且中国“男主外、女主内”的传统导致孩子多由女性养育,母亲延迟退休导致隔代照料时间减少,进而加剧了女性养育孩子的压力,导致生育意愿降低。

表11 母亲延迟退休与子女生育意愿的异质性分析
母亲延迟退休对未有生育行为的个体的生育意愿具有显著的负向影响,而对有生育行为个体的生育意愿影响不显著。这主要缘于未生育过孩子的个体面临着更大的不确定性和生育行为造成的潜在压力,母亲因延迟退休而降低隔代抚养水平,无异于雪上加霜,因此其生育意愿受母亲延迟退休的负向影响更显著。
与未就业成年个体相比,就业子女个体的生育意愿,更容易受到母亲延迟退休的影响。这主要是缘于,生育和养育孩子与工作之间存在很严重的冲突,而隔代照料可以缓解这一冲突。因此,母亲延迟退休对隔代照料时间的挤出效应对有工作的子女的生育意愿有更明显的负向影响。
依据子女年收入是否大于样本的中位数,本文将样本划分为高收入与低收入群体。由表11的结果可以看出,母亲延迟退休导致低收入子女的生育意愿显著降低,而未对高收入子女的生育意愿产生显著影响。这说明高收入的子女,在面对因母亲延迟退休而造成的隔代照料时间缩短时,更有动机采取托幼机构等社会照料方式照看孩子,因而母亲是否延迟退休对其生育意愿的影响不显著。
五、结论和政策启示
本文构建了一个包含内生生育率、隔代照料和延迟退休的世代交叠模型,用于分析延迟退休对于隔代照料和生育率的影响。基于2018年CFPS数据,本文检验了父代延迟退休对子女生育意愿的影响。得到的研究结论如下:
第一,理论分析表明,延迟退休对生育率有双重影响:一方面,延迟退休不但挤出老年个体提供的隔代照料时间,而且导致家庭抚养比率和老年个体家庭养老需求的降低,进而导致对孩子作为“投资品”属性需求的降低,二者均对生育率产生了负向的影响;另一方面,延迟退休导致老年个体收入增加,从而放松了其成年时期的时间约束,且延迟退休导致成年个体照料孩子时间的提升,二者均对生育率产生了正向的影响。综合来看,延迟退休对生育率的负向影响占据主导地位,因而导致随着退休年龄的延长,生育率逐渐降低。而劳动供给总量随着退休年龄的延长呈现出先上升后下降的倒U型变动趋势,在模型参数基准取值的设定下,劳动供给总量最大化的退休年龄约为62岁。
第二,实证分析表明,母亲延迟退休导致子女生育意愿显著降低,而父亲延迟退休对子女生育意愿的影响不显著。进一步的机制分析发现,一方面,延迟退休导致母亲隔代照料的概率降低,同时提供的隔代照料时间缩短,二者均对子女生育意愿具有负向影响;另一方面,母亲延迟退休增加了向子女提供的经济支持净额,对子女生育意愿产生正向的影响。母亲经济支持的增加未能补偿隔代照料的减少,最终导致子女的生育意愿降低。异质性分析的结果表明,母亲延迟退休主要对女性群体、就业群体、未生育群体和低收入群体的生育意愿产生显著的负向影响。
根据理论和实证分析的结果,本文关于延迟退休和生育率的政策启示主要包括如下:
首先,延迟退休政策导致生育率下降,这似乎与中国当前完全放开“三孩”生育政策的落脚点相悖,当然这并不意味着要否定延迟退休政策。延迟退休与全面“三孩”政策的侧重点各不相同,全面“三孩”意在长期改善中国人口结构、保持良性的人口增长,而延迟退休则是为了解决有效劳动力供给不足以及缓解养老保险的支付压力。从本文数值模拟的结果来看,延迟退休政策显著地增加了总劳动供给,说明延迟退休依然是积极应对人口老龄化、缓解有效劳动供给不足的有效措施。
其次,延迟退休会挤出老年人的隔代照料时间,使成年人照料孩子的时间禀赋更为紧俏,从而不利于生育水平的提高。目前,幼儿托育是抑制中国家庭生育率增长的一大阻碍。为此,政府部门在倡导老年人积极进行隔代照料的同时,大力发展普惠、高质量托幼服务事业,可以有效缓解生养子女与劳动供给,尤其是和适龄生育女性劳动供给之间的冲突,降低生育抚养孩子的机会成本。这将不仅有助于劳动供给的显著增加,而且有助于生育率的显著上升。
最后,生育决策是个体受各种因素影响后的内生最优选择,其中住房、医疗以及子女教育等方面的生育成本是制约生育意愿的重要原因。因此,政府部门应构建并完善生育支持体系,通过直接的生育补贴、减税激励等途径降低生育成本。同时,政府应深化住房改革以维持房价平稳,完善社会保障制度以缓解家庭养老压力,推动公立医院改革以降低医疗费用,积极落实学生减负以降低家庭教育支出,将有助于生育率的显著提升。
——基于人力资本传递机制
——基于子女数量基本确定的情形

