进气压力畸变对某涡轴发动机影响分析研究

杨宇飞 王召广 黄 兴 屠宝锋

（1.中国航发湖南动力机械研究所，湖南株洲 412002；2.南京航空航天大学 能源与动力学院，江苏南京 210016）

发动机气动稳定性是考核发动机的一个关键指标，其直接影响了飞机的使用和任务能力[1]。进气压力畸变是影响发动机稳定工作的最主要因素之一[2]。目前，国内关于进气压力畸变方面的研究主要集中在涡扇发动机[3-5]，针对涡轴发动机进气畸变的研究还比较少，而且涡轴发动机在进气畸变方面与涡喷、涡扇发动机也存在一定差异[6-7]。

本文基于经典平行压气机理论，引入周向掺混系数来考虑不同扇区间质量、动量和能量的交换；通过求解积分形式的、带源项的二维非定常欧拉方程，计算发动机内部的流动参数，再结合适当的稳定性判据，判断发动机在给定的进气畸变条件下是否发生气动失稳[8]。

1.计算模型

1.1 物理模型

本文针对某型涡轴发动机开展研究，根据对象的几何特点以及工程经验，建立圆柱坐标系计算域和网格。坐标系包括:周向、轴向和径向。但是大量研究已经表明径向畸变对发动机稳定性的影响比周向畸变小，可以忽略不计。因此，三维坐标简化为二维坐标系，模型简化及轴向单元划分如图1 和图2 所示。

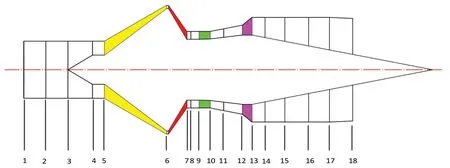
图1 轴流-离心式涡轴发动机简化模型

图2 周向计算单元

周向和轴向的控制单元将计算域划分为一系列单独计算单元，同时选择部件之间的交界面，建立整机的计算网格。周向上，将发动机沿周向等分成多个扇形块，并假定每个扇形块中的部件具有与完整部件相同的特性，相邻的轴向站和周向站之间构成一个控制体。

1.2 数学模型及求解方法

针对计算域中的每一个控制体，采用二维欧拉方程描述控制体内部的流动：

其中，g表示压气机或其他部件的引气或注气量，规定引气时g取负号，注气时取正号；下角标g表示引气或注气参数，θ表示周向分量。

直接对上述方程求解是十分困难的，为了满足本文提出的计算功能，引入了假设条件，对上式进行简化。引入向量=(,vθ,T,P)，上式可以写成：

此时，只要给定进口边界条件和初值，可以通过求解式（2）得到发动机相关截面参数和性能特性。

1.3 进口边界

本模型的采用综合压力畸变指数描述进口总压畸变，进口总压畸变条件包含有序的畸变和随机的动态畸变：

有序周向压力畸变P0＊(θ,t)又包括稳态压力畸变和非定常压力畸变两部分：

其中，P＊(θ)为稳态压力畸变。使用稳态压力畸变指数∆0来表示稳态压力畸变的强度，其表达式如下：

dP＊/dt(t-t0)为非定常压力畸变，随时间变化作用在整个进口截面上，可用来描述冲击波这一类阶跃式的总压等熵扰动。这种扰动对于涡轴发动机一般不会遇到，本文不予考虑。

动态总压畸变也可以称为面平均紊流度，表示总压脉动的定量特征，即总压空间不均匀度随时间迅速变化。其定义式如下：

本文采用由稳态畸变指数∆0和动态总压畸变指数εav相叠加的综合畸变指数W来描述综合总压畸变强度。当采用插板产生总压畸变时，总压畸变中含有稳态分量和动态分量。从试验数据看，两种分量的比值一般在0.4～0.6。因此总压畸变其表达式为：

1.4 失稳准则

压气机计算结果中出现负的轴向速度，则认为发动机超出喘振线工作，此时压气机失稳。

2.模型验证

涡轴发动机国军标通用规范中采用DC60 指数形式描述进气压力畸变，即假设发动机进口周向存在60°的低压区，计算公式如下：

其中，Pt,av,60表示发动机进口截面上、最低压力区60°扇形范围内的面平均总压；Pt,av表示发动机进口截面上的平均总压；0.5ρv2表示发动机进口截面上平均动压头，与来流的密度和速度有关。

试验中进气畸变模拟采用插板法[9-10]，获得DC60 指数。为对比计算和试验数据，必须将DC60 指数转换为周向不均匀度，然后假设动态压力畸变分量为零，再得到综合压力畸变指数。

在畸变试验过程中，环境总温301.3K，环境压力100500Pa，发动机处于中间状态，DC60=-0.4055。转换成综合压力畸变指数W=0.5346%。

表1 给出均匀进气下本模型和试验情况的对比，表2 给出了涡轴发动机中间状态在综合压力畸变指数等于0.5346%情况下的计算和试验结果。

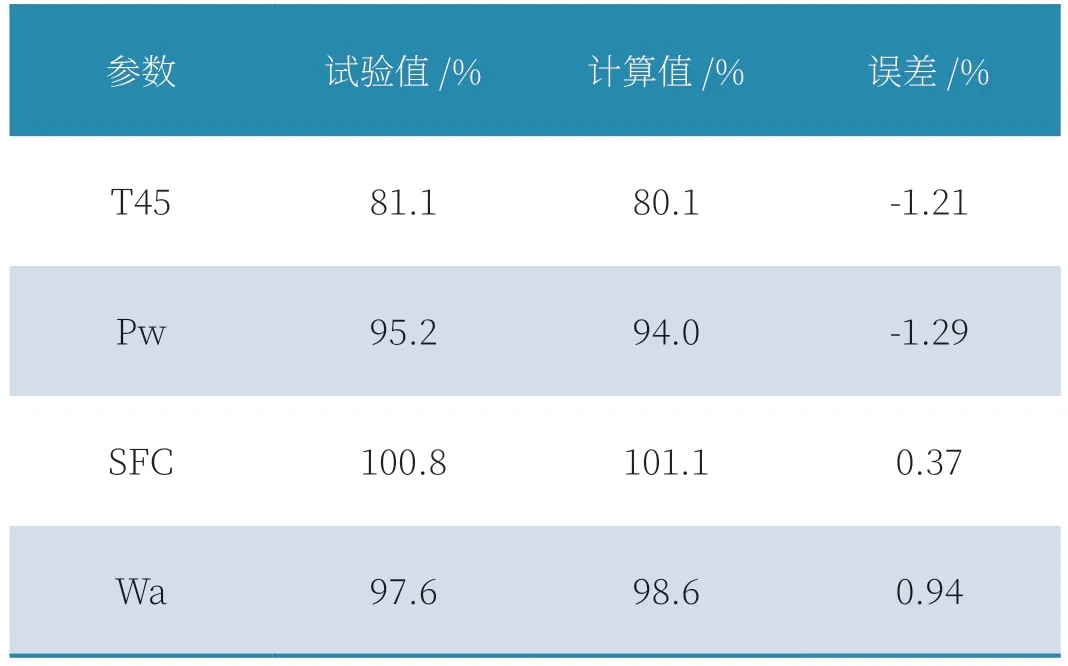
表1 中间状态均匀进气情况下试验和计算结果对比

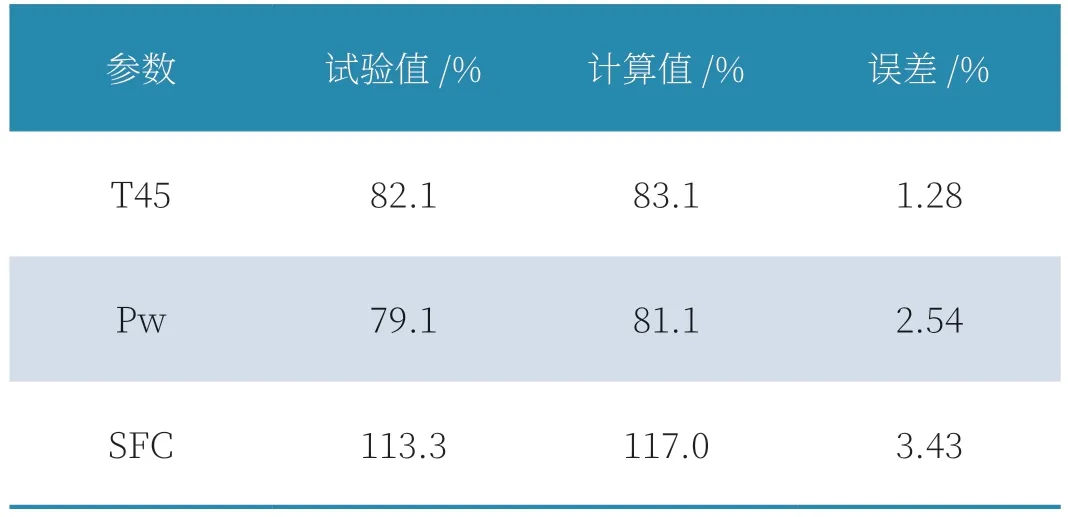
表2 中间状态W=0.5346%，试验和计算结果对比

可以看出在下本模型计算数据与试验值基本吻合，表明本模型的可以在一定程度上反映发动机真实畸变下的性能状态。

3.压力畸变对性能影响

3.1 对稳定性的影响

该涡轴发动机主要由轴流加离心式压气机、回流燃烧室、轴流燃气涡轮和动力涡轮组成。其正常工作线如图3所示。

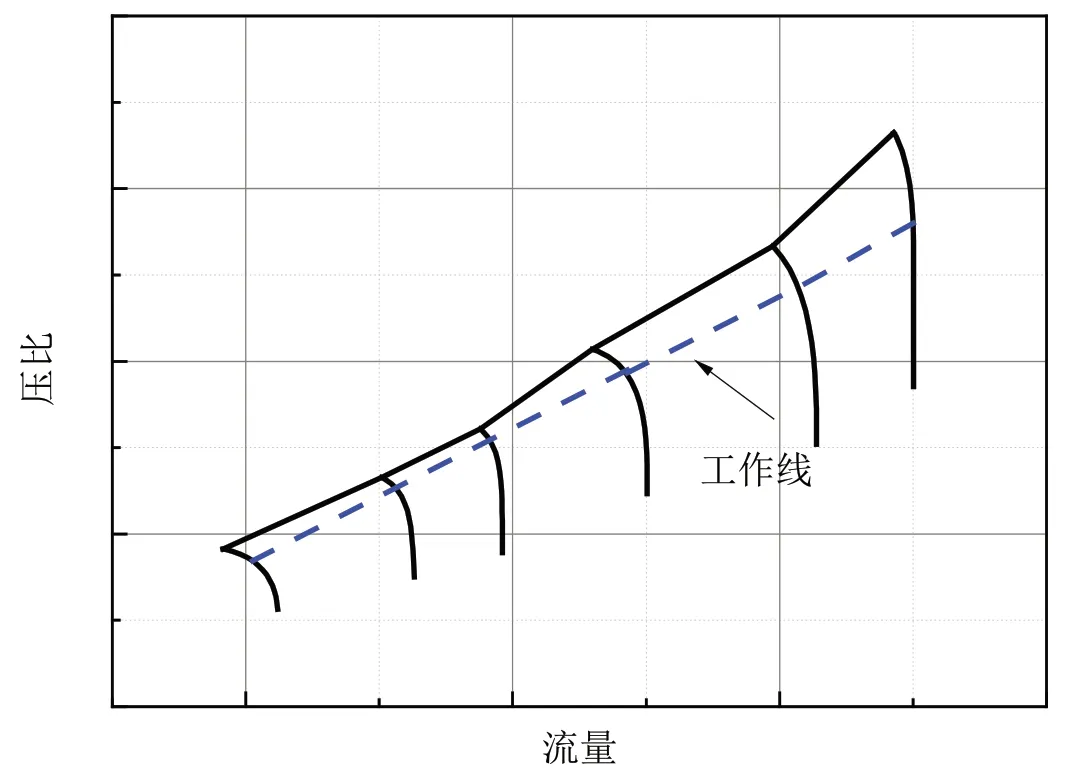
图3 发动机工作线

表3 给出了不同转速情况下的临界压力畸变指数和压力畸变敏感系数，随着转速降低，发动机原始可用稳定裕度逐渐减小、临界综合压力畸变指数也逐渐降低，压力畸变敏感系数逐渐增大，表明该发动机抗压力畸变能力逐渐变弱。

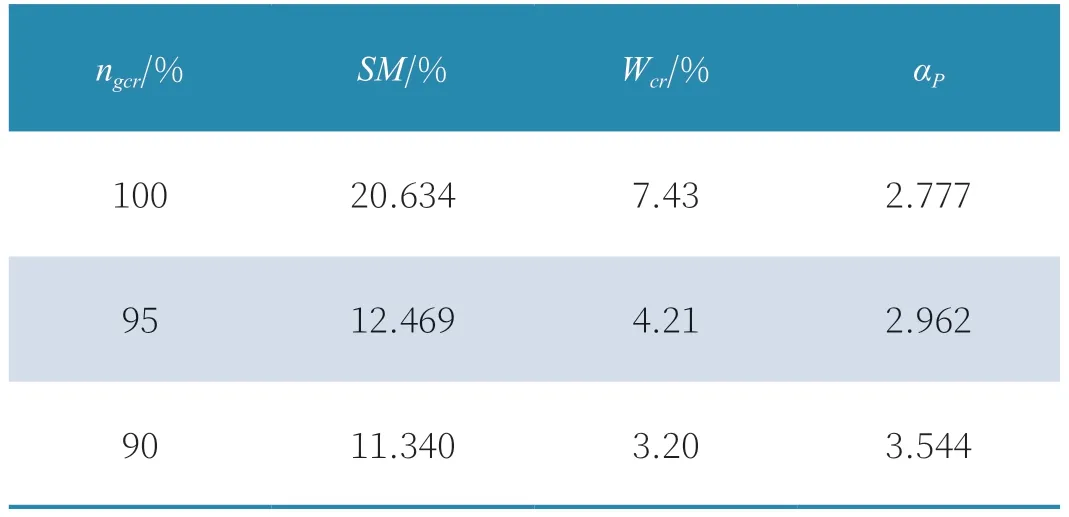
表3 不同转速下临界压力畸变指数和敏感系数

根据经验，发动机抗压力畸变能力大小与压气机特性线的陡峭程度有关，从图3 的组合压气机特性图就可以看出，随着转速降低，工作线斜率绝对值逐渐降低，陡峭程度变小，特性线越来越平缓，导致发动机抗压力畸变能力下降。因此在设计时，为提高发动机抗压力畸变的能力，需要尽可能提高共同工作点在等转速线上的斜率。

图4 给出了100%设计转速，在综合压力畸变指数等于5%时，稳态压力畸变指数沿轴向的传递过程。可以看出，压力畸变在压气机内传播时，快速下降。但流过轴流级出口后，在离心压气机又出现了回弹。经过离心压气机以后，压力畸变快速衰减，出口的压力畸变指数是进口的0.38 倍，衰减了62.08%。计算结果表明，该涡轴发动机进气畸变易发生在第一级轴流压气机以及离心压气机。

图4 稳态压力畸变指数的轴向传递

为验证发动机综合畸变指数随时间增长，发动机的工作情况。图5～图7 给出了100%设计转速时，综合压力畸变指数等于2%、4%、10%时，各扇区工作点在时间推进计算过程中瞬时位置的变化。其中扇区1 是高压区，扇区2 是低压区。

图5 W=2%各扇区工作点

图6 W=4%各扇区工作点

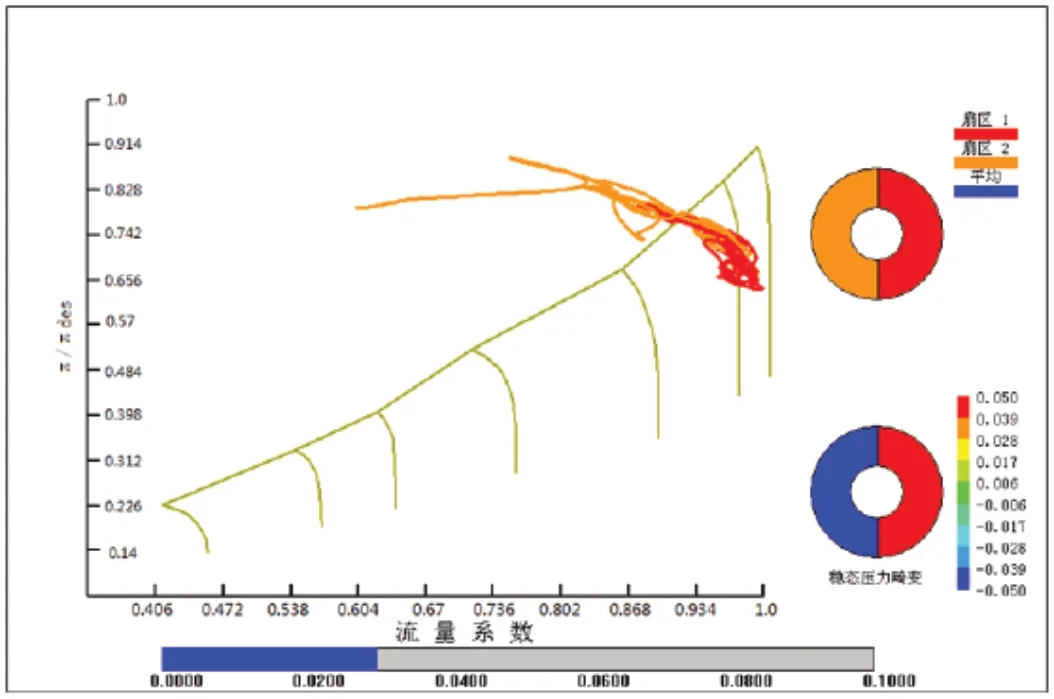
图7 W=10%各扇区工作点

可以看出，扇区1 在时间推进的过程越过稳定边界，但是最后又能够稳定在稳定边界左侧某个位置，并没有导致流量系数进一步降低，始终处于流量大于零的情况，因此发动机能够稳定工作。当综合压力畸变指数等于4%时，发动机最终能够稳定工作，但是，扇区1 和扇区2 工作点的脉动幅值比综合压力畸变指数1%要大。当综合压力畸变指数等于10%时，发动机两个扇区的工作点无法稳定在某个位置，流量快速降低，最终出现负速度，发动机气动失稳。

3.2 进气压力畸变对性能的影响

图8 给出了畸变区周向范围等于180 度时，100%设计转速时综合压力畸变指数分别等于1%、2%、3%、4%、5%、6%和7%时发动机的轴功率和排气温度。可以看出，随着综合压力畸变指数的不断增加，发动机输出的轴功率逐渐降低、排气温度逐渐提高。

图8 功率和T45随综合压力畸变指数的变化

4.结论

本文详细介绍了进口压力畸变对轴流离心组合式的涡轴发动机气动稳定性影响的计算方法，并对该涡轴发动机在典型进口压力畸变作用下的稳定性和性能进行了计算，结果表明：

（1）由于该涡轴发动机最大状态下压气机流量裕度小，导致转速较低时的抗压力畸变能力较弱。

（2）相同转速和压力畸变条件下，该发动机畸变发生位置易出现在第一级轴流压气机或离心压气机处。

（3）随着综合压力畸变指数的不断增加，发动机输出的轴功率逐渐降低、排气温度逐渐提高。