基于速度风险势场的高速公路行车风险甄别方法

王博，张驰，任士鹏，刘昌赫，谢子龙

(1.长安大学 公路学院，陕西 西安 710064；2.教育部公路基础设施数字化工程研究中心，陕西 西安 710000；3.南洋理工大学土木与环境学院，新加坡 639798；4.广东省交通规划设计研究院集团股份有限公司，广东 广州，510630)

随着道路监控、电子不停车收费及高清卡口等设施全面普及，目前我国高速公路管理已经进入数字化时代.按照国务院安委会发布《道路交通安全“十三五”规划》[1]，截止2020年底全国各运营公司均已完成运营监控调度中心建设，全国高速公路已基本实现实时监控全覆盖.面对种类繁杂的海量信息，如何快速甄别出重点管控的高风险路段成为新的挑战.根据高速公路安全管理“精准监测、动态管控及快速反应”的需求，研究高速公路行车风险甄别方法，对于智慧感知设备布局、重点监测路段划分和交通管控决策具有重要意义.

车辆在行驶过程中，驾驶人通过感知障碍物距离和惯性力等信息对行车风险进行判别.驾驶人根据感知到的行车风险，会改变车辆速度或轨迹，以主动降低行车风险[2]，即车速在路域空间上的分布规律能够在一定程度上反映行车风险.自1964年起，学者们从不同角度研究车辆速度对行车风险的影响[3].相关研究可以分为风险机理和事故相关性2个方面，其中关于风险机理的研究，学者们从“人、车、路”等角度尝试诠释速度对行车风险影响的内在规律，提出“视距理论”[4]、“安全距离理论”[5]、“车辆动力学”[6]和“交通冲突”[7]等理论；在事故相关性方面，学者们通过统计学方法分析速度与交通事故的相关性，相关统计指标包括速度绝对值[8]、速度离散度[9]、运行速度[10]等.基于风险机理的评估方法，能够对风险类型进行有效甄别，但是风险致因考虑较为单一，风险评估结果不全面.基于速度统计指标的评估方法能够较为全面地表征行车风险，但是受数据采集方法的限制，速度在二维空间的分布情况研究较少.得益于卫星导航、高清卡口等技术的发展，车速数据的监测效率和精度不断提高[11].采用这些技术能够获取车速在路域空间的纵向和横向分布数据，为更深层次的行车风险的分类甄别研究奠定了良好的数据基础.

21世纪初期，人工智能领域率先引用势场理论提出“虚拟引力场”并应用于机器人行为规划.近年来自动驾驶技术的相关学者，将势场理论引入交通领域，为行车风险研究提出了新的思路.目前势场理论在交通领域的相关研究主要有道路势场、车辆动能场和驾驶行为场3个方面.在道路势场方面，Wolf等[12]考虑车道标线和道路边界等因素对行车的影响，采用类高斯函数建立道路侧向的车道势场计算模型；在车辆动能场方面，Woo等[13]以车辆速度、距离和角度等参数建立车辆动能场模型，结合车辆轨迹预测分析相邻4个车辆对车辆换道风险的影响，提出一种换道风险评估方法；在驾驶行为场方面，陶鹏飞等[14]在分析驾驶人心理特点的基础上，结合人工势场理论提出吸引力模型和排斥力模型，建立包含减速停车、启动加速和常态行驶3种运行状态的跟驰模型.目前，清华大学王建强等[15-16]在行车风险研究中引入势场理论，提出安全势场理论.安全势场在融合“人-车-路-环境”各类风险因素和统一风险刻画方法方面具有明显优势，并且为路域二维空间内的行车风险分析提供新的思路.

行车风险甄别包括高风险路段的空间定位、风险分类和量化、现有行车风险甄别方法在宏观层面较难实现风险分类.因此，为了更好地实现宏观层面的行车风险甄别，本研究分析车辆速度空间分布规律，结合道路线形、速度梯度对行车风险的影响，引入势场理论，提出速度风险势场理论.在综合考虑速度分布特征、道路圆曲线半径及纵坡等因素下，以行车风险甄别为目标，提出基于速度风险势场的高速公路行车风险甄别方法，建立速度势能场和速度风险势场强度计算模型.为了验证评价效果，以西南地区某高速为实例进行行车风险甄别，对比了2处路段的甄别效果，证明速度风险势场能够对高速公路行车风险进行有效甄别.

1 数据采集与处理

以西南地区某高速公路共66.5 km路段为数据采集对象，收集高清卡口道路断面监测数据共124216组，高速公路事故数据共计439组.高清卡口实测道路断面共计4处分别为K2084、K2088、K2110和K2114，累计监测时长为31 d，其中每组监测数据包括车牌、车型、行车方向、时间、速度及车道等，筛选出的断面监测数据如表1所示，其中，T为经过时间，v为速度.高速公路事故数据统计时长为4 a，其中每组事故数据包括时间、桩号、行车方向、事故车型及事故类型等，筛选出的事故数据如表2所示.

表1 西南地区某高速道路断面监测数据Tab.1 Cross section monitoring data of expressway in Southwest China

表2 西南地区某高速公路事故数据Tab.2 Accident data of expressway in Southwest China

本研究利用Python程序采集百度地图POI数据共计91955组，每组数据包括坐标、监测时间、路段长度及行程时间，根据路段长度和行程时间，进一步计算路段平均车速.为了验证监测数据精确度，路段长度设置分别为30.0、16.0、8.0、4.0、2.0、1.0和0.5 km，其中1组30 km路段起终点设置于2处门架处，通过与实测数据对比分析发现，当路段长度为30 km时，得到的行程时间与门架监测得到的平均行程时间，误差为16 s，满足实际需求.随后以30 km为标准，划分路段监测行车数据，对路段长度为16、8、4和2 km的行程时间进行递推修正，最终得到2 km路段长度的路段速度数据.

2 数据分析

2.1 速度数据分析

实测路段大小车限速均为80 km/h，实行客货分离管制措施，外侧车道为货车专用车道.K2084断面高清卡口位于小半径曲线段（曲线半径R=340 m），K2088断面高清卡口位于连续S型曲线段（R=620 m），K2110断面高清卡口位于直线段，K2114断面高清卡口位于曲线段（R=870 m）.在同一时间内，对高清卡口获取的车辆速度v进行统计，得到K2084、K2088、K2110和K2114断面处车辆的75%、50%、25%分位值和平均车速，并与百度POI获取的速度数据进行对比，如图1所示，其中v为高清卡口或百度POI获取的车速数据.结果显示百度POI获取的路段车速与高清卡口获取的内侧车道车辆平均速度较为接近.

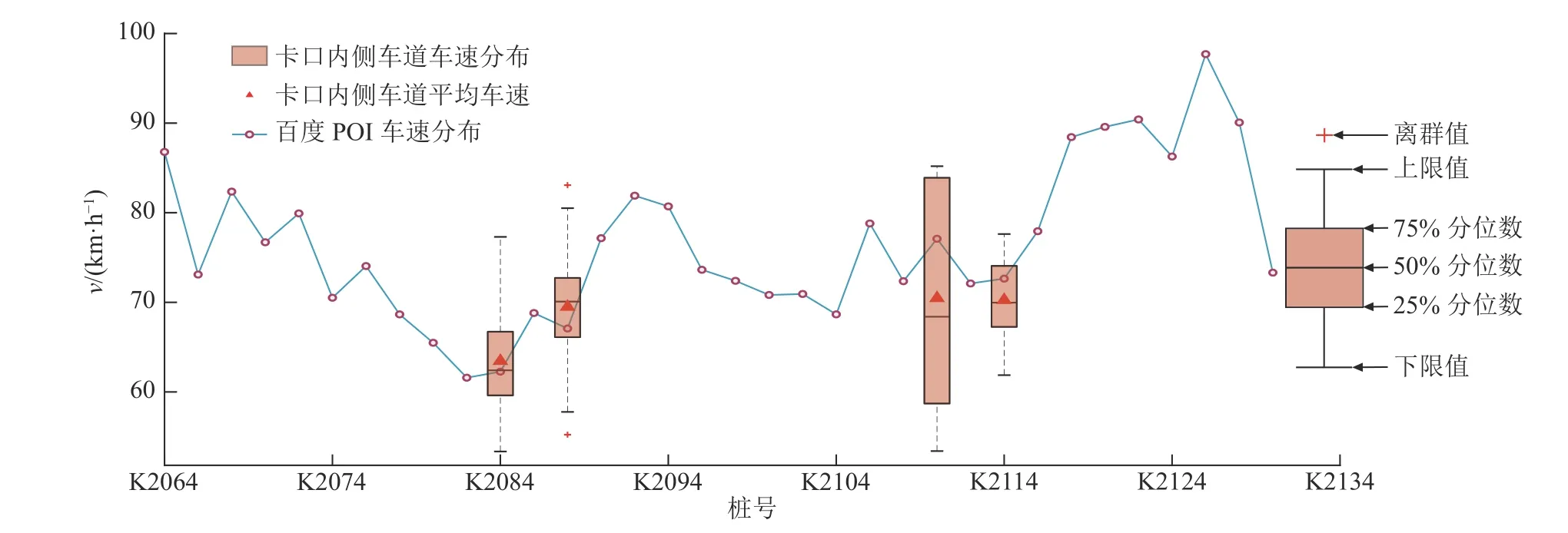
图1 来自百度POI和高清卡口的车速数据对比Fig.1 Comparison of vehicle speed data from Baidu POI and HD bayonet

按照车道和时间进行分类统计，卡口采集的横断面车速结果如表3和图2所示，其中sd为速度标准差，时间T统计时间段为7:00—20:00.对比4处断面车速统计结果得出以下结论.1）清晨和傍晚4处断面的车速变化趋势相同.当7:00—9:00时，车速具有明显的增加趋势；当18:00—20:00时，车速具有明显的减小趋势；其余时段，各断面车速随时间变化无相同趋势.2）同一断面处内、外侧车道的平均车速和车速离散度随时间变化趋势基本一致.K2084断面在15:00时，内、外侧车道的平均速度均位于峰谷，速度离散度最大时段均位于8:00；K2088断面，12:00—17:00内、外侧车道的平均速度和速度离散度变化趋势一致；K2110断面，除14:00—17:00外，其余时间段内、外侧车道的平均速度和速度离散度变化趋势基本一致；K2114断面，除13:00和15:00外，其余时段内、外侧车道的平均速度和速度离散度变化趋势基本一致.3）直线段较曲线段车速离散度高，并且内侧车道相比较外侧车道车速离散度高，曲线段内、外侧车道离散度相近.K2110断面位于直线段，内、外侧车道的车速标准差sd均远大于其他断面，且内侧车道较外侧车道高.4）内、外 侧车道平均速度比值Rlane基本一致，接近0.85.

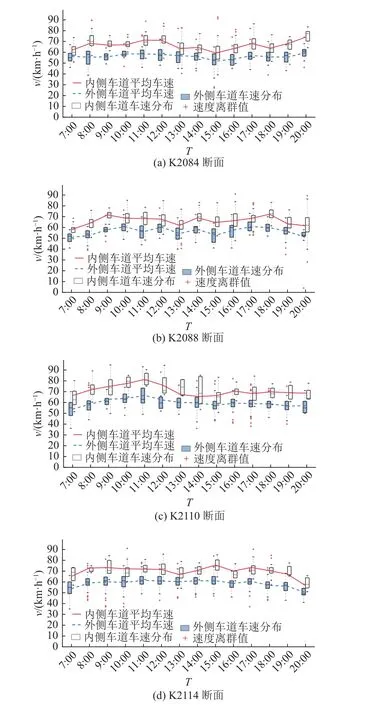
图2 断面车速时间和空间分布特征分析Fig.2 Time and space distribution characteristics analysis of vehicle speed on road cross-sections

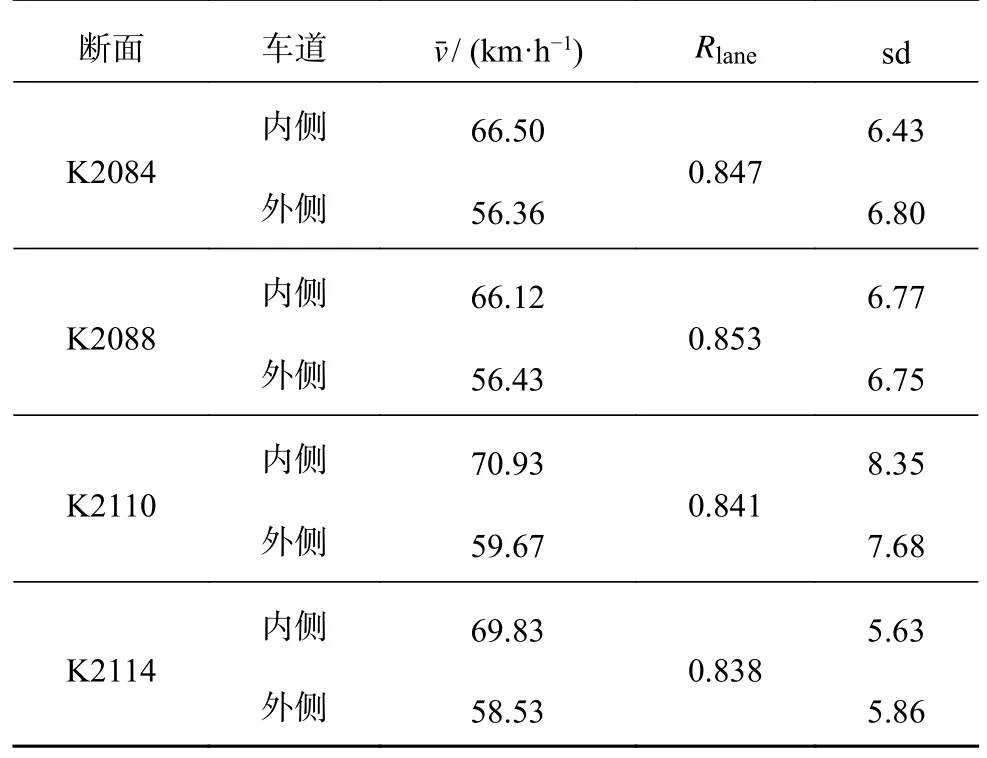
表3 断面车速统计Tab.3 Cross section vehicle speed statistics

2.2 交通事故数据分析

2.2.1 速度梯度与交通事故 Shoarian等[17]研究交通流相关参数与交通事故的相关性，发现速度梯度对交通事故风险具有较高的影响度.在我国《公路项目安全性评价规范》（JTG B05—2015）[18]中，以运行速度梯度的绝对值作为运行速度协调性评价指标.Zhu等[19]对比设计速度、运行速度、加速度及速度梯度等速度相关安全性指标，结果表明车辆速度梯度评价效果优于其他指标.对比交通流速度梯度G与交通事故的分布规律，如图3所示，图中Na为事故数.交通流速度梯度分布和交通事故分布有一定的趋同性，但是在K2085～K2105相关性较低.

图3 交通流速度梯度与交通事故分布Fig.3 Distribution of traffic velocity gradients and traffic accidents

2.2.2 道路纵坡与交通事故 纵坡是影响高速公路交通安全的重要指标，坡率与交通事故数正相关[20].道路纵坡对交通安全的影响，主要用于车速和车辆制动能力.对于上坡路段，坡率越大，不同车型爬坡能力不同，容易引起速差较大，车辆换道超车概率增加；对于下坡路段，坡率越大、坡长越长，车辆制动行为越频繁，并且制动距离越低.马聪等[21]对比了曲率半径和道路纵坡对事故预测的影响，认为道路纵坡对山区高速公路的影响更高、Ahmed等[22]的研究结果显示下坡路段较上坡路段事故率更高，对比道路平均纵坡与交通事故的分布规律，如图4所示.结果表明平均纵坡小于2%的路段事故数明显小于其他路段，与林宣财等[23]的研究结果一致.此外，事故数最高的路段位于K2118～K2130下坡路段中部.

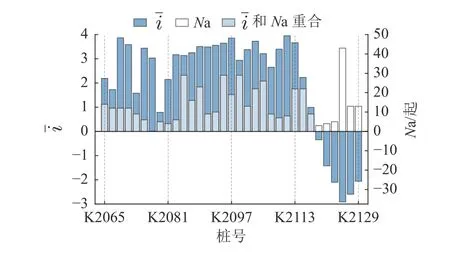
图4 道路纵坡与交通事故分布Fig.4 Distribution of vertical slope and traffic accidents

2.2.3 平面半径与交通事故 曲线段行车风险主要包含侧滑、侧偏和侧翻等侧向风险，风险大小与道路半径呈负相关[24-25].为了对比道路半径对交通事故的影响，取道路不设超高的圆曲线最小半径规范值R* [26]与道路平面半径R比值为道路平面曲率参数α：

当R≥R*时，与直线段相近对行车安全影响不大的α取值为1.0，α与行车风险呈正相关.曲率参数α和交通事故的分布规律对比，如图5所示，可以发现道路平面曲率参数分布与事故分布具有较高的相关性.

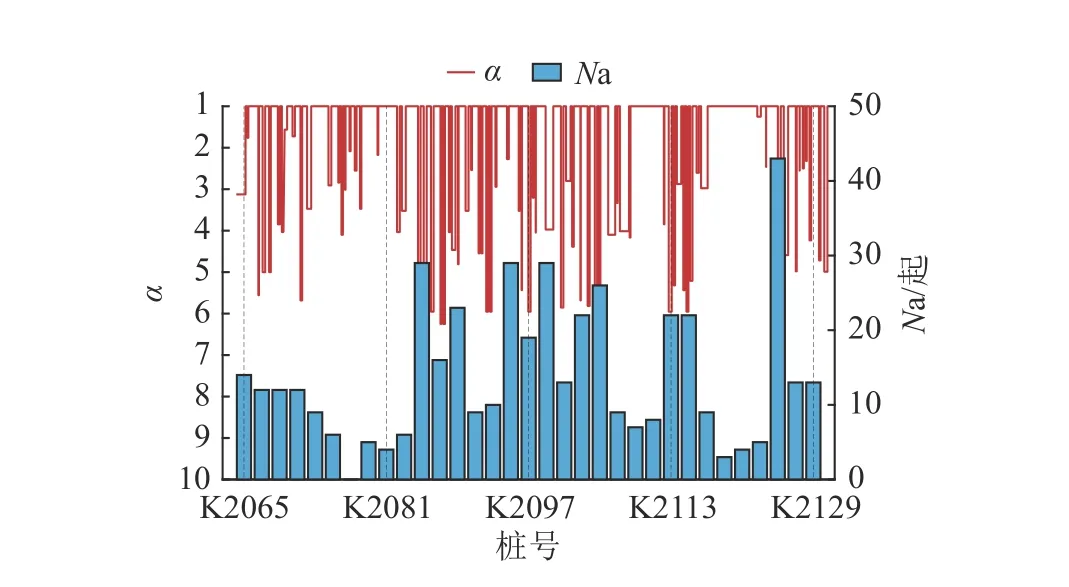
图5 道路平面曲率参数与交通事故分布Fig.5 Distribution of road horizontal curvature parameters and traffic accidents

3 行车风险甄别方法

3.1 行车风险与车辆运动

在道路行驶过程中的车辆可以分为“目标车辆”与“环境车辆”，被观察的单个车辆为目标车辆，除去目标车辆之外的所有车辆共同组成环境车辆.由驾驶人或自动驾驶系统所控制的目标车辆，能够通过识别与周围车辆速差和距离，对行车风险进行感知[27].在行驶过程中，目标车辆与环境车辆的相对速度越小，即与环境车辆速度越接近，事故风险越低[28]；目标车辆与环境车辆的绝对速度越低，车辆制动所需距离越短，同时事故严重程度越低[29].舒适性也是风险感知的一种，车辆在行驶过程中加速度和离心力对驾驶人舒适性造成影响[30].行车风险除去需要遵循上述内容外，还会受道路线形、构造物、交通管制、气象及交通流措施等多类因素共同影响.在感知到风险后，驾驶人会通过控制车辆速度和行驶轨迹，以避免产生交通事故.结合速度数据分析结果，可以假设在自由流状态下，相似条件和环境下的车速选择趋近相同，即同一时间段和同一路段内多数车辆速度趋近一致[31-32].

3.2 速度风险势场

势是场产生的力按作用力方向的积分，场强是势能按作用力方向的梯度.行车风险可以利用场的形式表达，同时可以刻画风险源的位置和强度.根据牛顿第一运动定律“任何物体都要保持匀速直线运动或静止状态，直到外力迫使它改变运动状态为止”.当车辆在驶向风险源时，车辆会降低速度；当车辆在驶离风险源时，车辆会增加速度.这种运动状态的改变可以视为车辆受到“外力”作用，即车辆受风险场的影响.

本研究提出的速度风险势场，以速度变化趋势为基础，考虑道路线形对行车风险的影响，利用势场理论刻画道路行车风险在路域范围内的分布规律.速度风险势场包含速度势能和速度风险势场强度2部分，如图6所示.基于同一时间段和同一路段内多数车辆速度趋近一致的特性，提出交通流在某一位置处的速度选择趋势为速度势能P.速度势能场的场强即为速度梯度，可以描述路域空间中各方向的速度变化的剧烈程度.在速度势能沿侧向和纵向的梯度变化基础上，叠加道路纵坡和平面半径对行车风险的影响，构建速度风险势场强度E，描述该位置处车辆行车风险的大小和方向，表征路段行车风险分布情况.

图6 公路速度风险势场概念图Fig.6 Conceptual map of highway velocity risk potential field

3.2.1 速度指标选择 关于交通流速度的统计指标较多，例如15%位车速、50%位车速、85%位车速.已有研究证明[33-34]，在自由流和路段限速状态下，车道断面速度频率分布符合正态分布，在限速状态下车速离散性降低.平均速度能够更好地描述驾驶人的速度选择趋势，因此基于平均速度构建速度势能指标.

3.2.2 模型构建基础 速差和事故率之间的关系一直是交通安全研究的重点，相关学者提出Solomon曲线等一系列成果[35]，通过速度这一指标，将微观风险模型与交通事故统计联系起来[36].根据第2章数据分析可知，速度梯度、道路半径、纵坡与交通事故分布具有一定相关性.纵向行车风险以跟驰过程中的追尾事故风险为主，主要风险表征为纵向安全距离不足，所需的纵向安全距离受前、后车辆速差和制动性能影响.道路纵坡影响车辆制动能力，速度梯度直接表征所需的纵向安全车距.侧向行车风险以侧向滑移为主，这样容易发生侧撞事故，主要风险表征为侧向安全距离不足.根据波良可夫模型、斯特拉霍夫经验公式[37]及Qu等[38]的研究，侧向相邻车辆所需的侧向安全距离与车辆的速差存在正相关，即相同侧向车距情况下相邻车辆速差越大，所需安全车距越大.车辆速差与距离的比值为侧向速度梯度，侧向速度梯度越大，行车风险越高.

结合第2章分析结果，本研究将道路纵坡和纵向速度梯度作为纵向风险评价参数，将道路半径和侧向速度梯度作为侧向风险评价参数.提出的速度势能场是基于路段纵向车速建立的，沿纵向的场强大小即为纵向速度梯度，沿侧向的场强大小即为侧向速度梯度.因此，在速度势能场基础上，计算不同方向速度势能场强，进一步可以考虑道路纵坡及半径对行车风险的影响规律，构建速度风险势场，以评估、刻画纵向和侧向的行车风险.

3.3 计算模型及参数标定

3.3.1 速度势能 采用路域范围内各路段的平均速度作为速度势能，路侧护栏处速度势能为0.当已知路段各车道车速时，直接采用各车道速度数据计算速度势能.当无法获取车道级速度数据时，可根据式（2）进行全域速度势能计算：

式中：Py,x为横向位置x处，纵向位置y处的速度势能，单位为km/h；Py为纵向位置y处全部车道的平均速度；φx为侧向分布系数，与车道数和侧向位置有关.

相关研究[39-41]已经证明，不同车道的平均速度沿道路侧向由内向外递减，车道间的速度差与车道数类型、及路段车型呈比例线性相关.在陆建等[42]和吴明先等[43]的研究结果基础上，结合表3中的统计结果，可以总结得出：双四车道的内、外侧车道平均速度比例为1.00∶0.85；双向六车道的内、中、外侧车道平均速度比例1.00∶0.90∶0.75.此外，结合驾驶人的换道和超车行为特性，以及侧向净距对驾驶人的心理效应，车道分隔线位置处车速可以认为是2个车道平均速度的均值；同时考虑到右侧硬路肩与左侧路缘带相比较宽，并且在无障碍物的情况下，速度降低情况较小，侧向分布系数φx具体取值如表4所示.

表4 速度势能侧向分布系数取值表Tab.4 Value table of lateral distribution coefficient of velocity potential energy

3.3.2 速度风险势场强度 势场具有方向性，其中纵向速度、风险势场方向与加减速趋势一致，即低势能指向高势能位置.考虑到我国高速公路外侧车道车速一般低于内侧车道的情况，侧向速度风险势场在直线段和右偏曲线段以低势能指向高势能位置为方向，在左偏曲线段考虑横向力方向为由内侧指向外侧，因此侧向速度风险势场方向左偏曲线段与直线段相反.在此基础上，提出速度风险势场强度计算方法：其中采用道路平面曲率参数作为侧向风险影响因子α，

式中：U为路段起终点的速度势能差，单位为km/h；η为速度风险势场强度系数；β为纵向风险影响因子；为路段平均纵坡；ΔH为路段的 高度差，单位为m；dx和dy分别为指向侧向和纵向距离，方向由低势能指向高势能位置，dx单位为m，dy单位为km；Ev为空间速度风险势场强度，具有大小和方向；Ex和Ey分别为侧向和纵向的速度风险势场强度；k为风险方向调整系数.

速度风险势场强度表征车辆受到“吸引力”和“排斥力”的大小和方向，即环境车辆平均速度对驾驶人速度选择的影响大小.速度风险势场强度与车速的离散性相关，速度离散性越小驾驶人速度选择趋近平均速度的几率越大.速度离散性的描述指标主要采用速度标准差sd和速度变异系数CV，其中速度变异系数CV指速度标准差与平均速度的比值，值越大代表离散度越大[44].由于离散度越大，速度风险势场强度越小，因此采用速度变异系数CV的倒数作为速度风险势场强度系数η：

侧向速度风险势场强度Ex和纵向速度风险势场强度Ey作为行车风险评价指标时，分别甄别侧向和纵向行车风险.在单一方向速度风险势场强度的基础上，构建空间速度风险势场强度Ev表征路段综合行车风险.由于各方向速度风险势场强度计算值范围和风险阈值存在不一致，同时还需要考虑不利情况，即侧向和纵向速度风险势场强度其中一个为0，另一个超过风险阈值时，空间速度风险势场强度依旧对风险进行有效判别.构建空间速度风险势场强度时，引入风险方向调整系数k，实现空间行车风险有效评估，风险方向调整系数和空间速度风险势场强度阈值公式为

式中：ex、ey、ev分别为侧向、纵向和空间速度风险势场强度的风险阈值.

4 高速公路行车风险甄别

4.1 指标参数计算

选取K2084断面28 d中10:00—20:00的实测数据，以小时为单元统计速度变异系数CV，计算结果如图7所示，图中N为CV的统计单元数量.根据结果可知，速度变异系数CV基本在0.05～0.17，最终取速度变异系数为0.10，计算速度风险势场强度系数η=10.该路段设计速度为80 km/h，不设超高时最小圆曲线半径为2500 m，侧向和纵向风险影响因子根据式（1）和（6）计算，计算结果如表5所示.

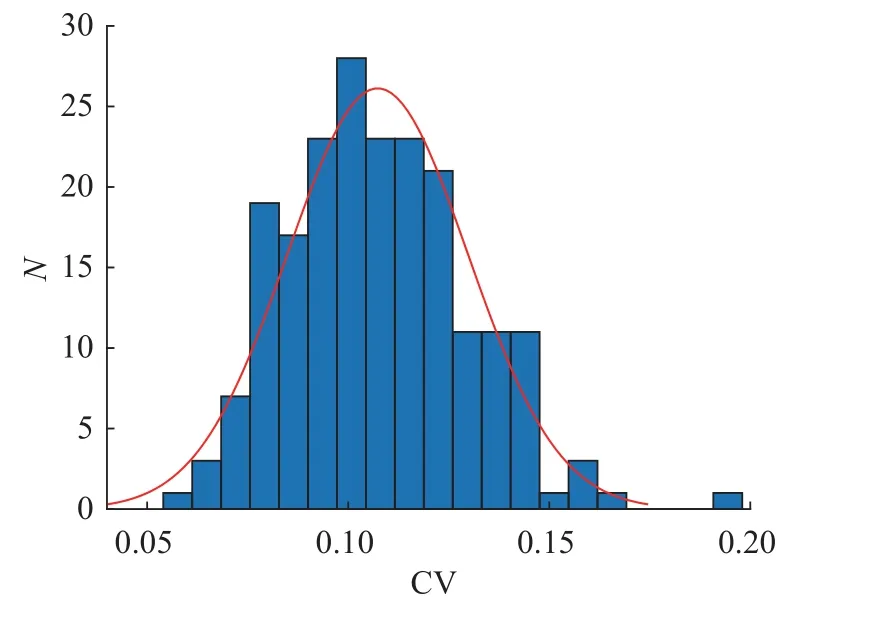
图7 K2084断面车速变异系数时间分布统计Fig.7 Temporal distribution statistics of vehicle speed variation coefficient for cross-section K2084

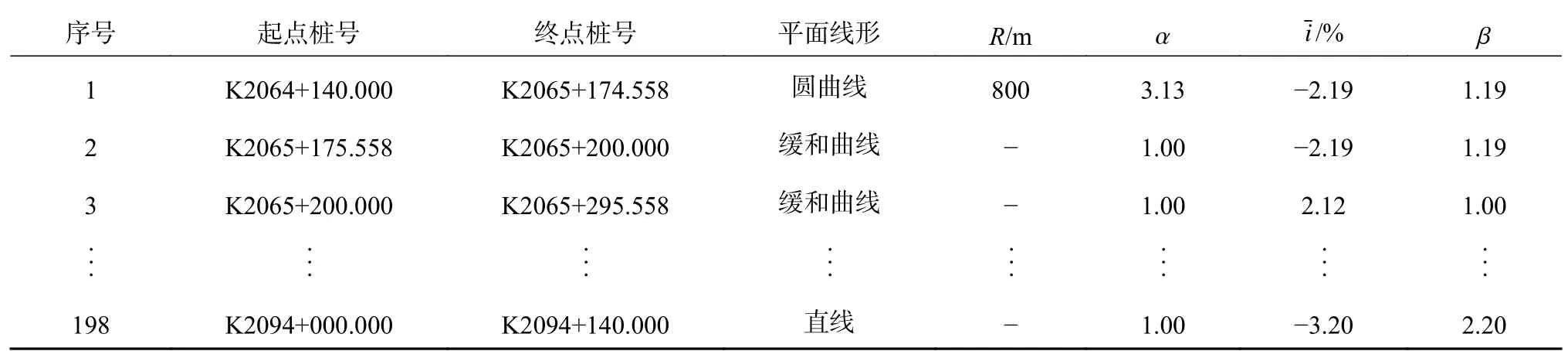
表5 K2064+140～K2094+140路段侧向和纵向风险影响因子计算表Tab.5 Calculation table of lateral and longitudinal risk impact factors for road section K2064+140 to K2094+140

4.2 行车风险甄别

为了研究基于速度风险势场的行车风险甄别方法，根据式（4）和（5），选取前述调研的西南地区某高速公路K2064+140～K2094+140路段为实例分析路段，进行速度风险势场相关计算.利用前述获取的百度速度数据，结合表4中的测向分布系数，构建速度势能矩阵，计算得到速度势能分布和速度风险势场强度分布.

根据所收集事故数据，进一步筛选出K2064+140～K2094+140路段，有记录事故共计157起，按照事故车型分类可分为3组，分别为有小型车事故89起、有大型车事故60起和大型车与小型车事故8起；按照事故形态分类可分为3组，分别为与侧向风险相关事故（撞击护栏、侧撞事故、操作不当）48起、与纵向风险相关事故（追尾事故）29起和形态不明事故80起.此外，事故数据缺少车道信息，根据现场调研情况该路段采取客货分离管制措施.在一般情况下，大型车行驶于外侧车道，小型车行驶于内侧车道，同时考虑车辆行驶一般靠近中心线位置，常见车辆宽度为1.8 m.为了方便研究，事故点取车道中心线左右0.9 m位置，仅有小型车事故位于内侧车道，涉及大型车事故位于外侧车道.K2064+140～K2094+140路段的速度风险势场强度及相关事故分布如图8所示.

由图8（a）可知，交通事故在K2068、K2085和K2088等场强峰值处出现聚集现象.考虑48起侧向风险有关事故，对所处位置的侧向速度风险势场强度Ex进行统计（以下速度风险势场强度相关统计均取绝对值），最大值为244.2，最小值为16.6，均值为75.5，所处位置Ex大于均值的事故共计16起，占比为33%.由图8（b）可知，交通事故在K2065和K2088这2个场强峰值处出现聚集现象.考虑29起纵向风险有关事故，对所处位置的纵向速度风险势场强度Ey进行统计，最大值为141.20，最小值为5.12，均值为74.60，所处位置Ey大于均值的事故共计15起，占比为51.72%.

图8 K2064+140～K2094+140路段3种速度风险势场与车辆交通事故的分布Fig.8 Three velocity risk potential fields and distribution of vehicle traffic accidents on K2064+140～K2094+140 section

速度风险势场强度越大，事故可能性越高.为了有效甄别行车风险，选取事故所在位置处速度风险势场强度的均值作为风险阈值，即侧向速度风险势场强度的风险阈值ex=75.5，纵向速度风险势场强度的风险阈值ey=74.6.当所处位置速度风险势场强度大于风险阈值时，代表发生对应风险相关事故可能性较高，即为侧向或纵向高风险路段.在K2064+140～K2094+140路段中，共甄别出13.85%的路段为侧向高风险路段，区域内发生了33.33%的侧向风险事故；16.26%的路段为纵向高风险路段，区域内发生了51.72%的纵向风险事故.

侧向速度风险势场和纵向速度风险势场均能够从单一角度对路段行车风险进行甄别，为了更好地实现路段行车风险评估，综合考虑侧向和纵向行车风险，根据式（7）计算空间速度风险势场强度，进一步作为路段宏观风险评价指标.结合式（9），取风险方向调整系数k=1.01，空间速度风险势场强度Ev及相关事故分布如图8（c）所示.

根据式（10）可知，空间速度风险势场强度风险阈值为106.8.进一步统计可知，高于风险阈值的区域内发生了45.86%的历史交通事故，42.42%的形态不明事故，60.07%的纵向风险事故，40.00%的侧向风险事故.空间速度风险势场甄别出的高风险路段，涵盖了侧向、纵向速度风险势场甄别出的高风险路段，并且能够进一步对风险构成复杂的高风险路段进行有效甄别.因此，根据速度风险势场强度与交通事故具有较高相关性，在一定程度上对高速公路行车风险进行空间刻画，综合运用侧向、纵向和空间速度风险势场能 够对行车风险甄别.

4.3 有效性验证

为了验证速度风险势场在高速公路行车风险甄别中的有效性，选取K2094+140～K2130+640路段作为有效性验证路段，采用上述方法进行路段风险甄别，进行方法有效性验证.速度风险势场强度系数η = 9.5.该路段事故总数为282起，其中与侧向风险相关事故56起、与纵向风险相关事故76起和形态不明事故150起.速度风险势场强度及相关事故分布如图9所示可知，事故分布与速度风险势场强度分布具有一定规律性，侧向风险相关交通事故分布与侧向速度风险势场强度分布具有明显规律.

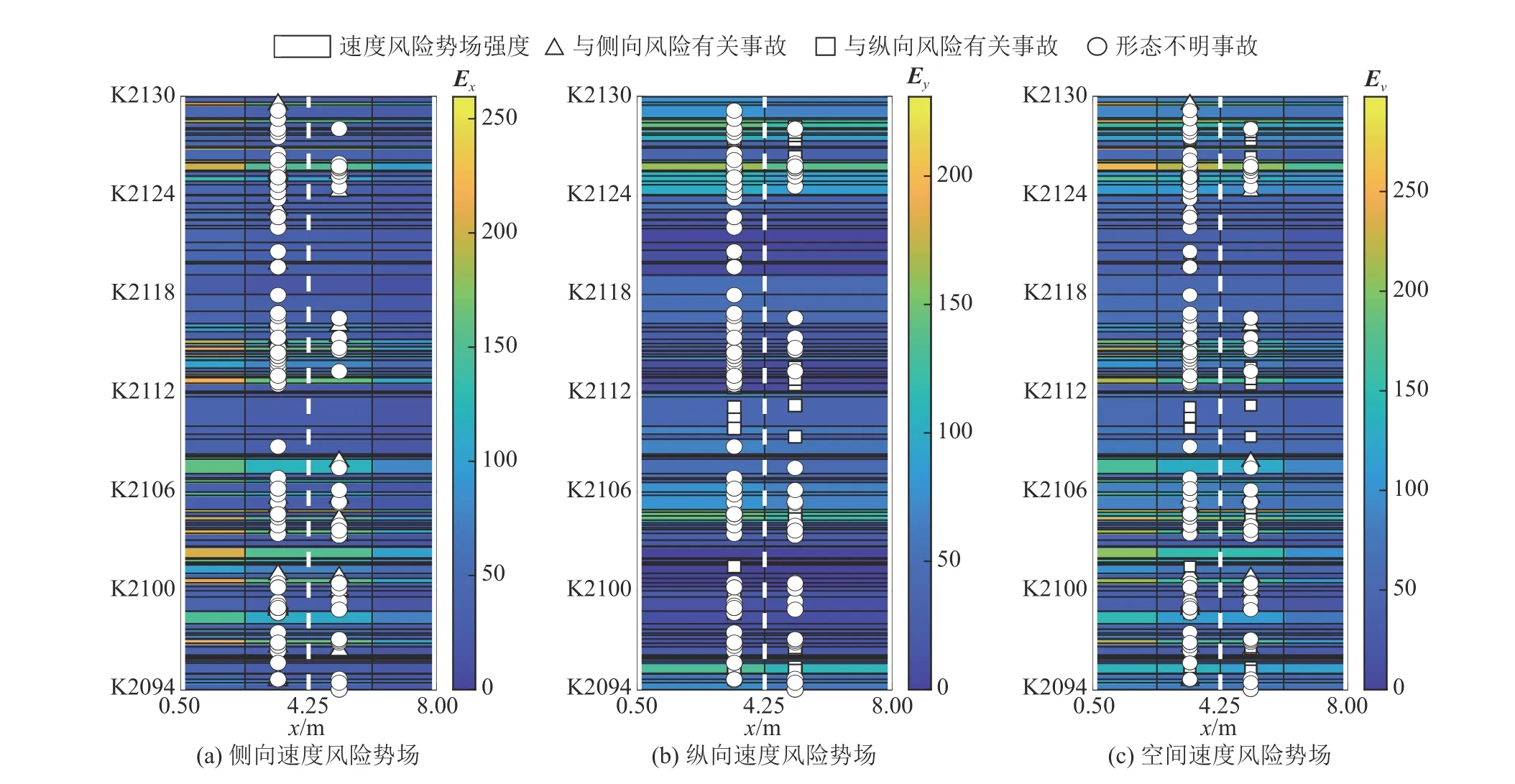
图9 K2094+140～K2130+640路段3种速度风险势场与车辆交通事故的分布Fig.9 Three velocity risk potential fields and distribution of vehicle traffic accidents on K2094+140～K2130+640 section

风险阈值采取前述统计结果，即侧向、纵向和空间速度风险势场的阈值分别为75.5、74.6和106.8.将3种速度风险势场强度的甄别效果进行统计对比，统计结果如表6所示.甄别效益比为总体事故甄别比例与大于风险阈值路段占比的比值.空间速度风险势场甄别出的高风险路段占比为24.33%，甄别出的事故比例为43.26%，甄别效益比为1.78.

表6 基于3种速度风险势场强度的高风险路段甄别效果对比Tab.6 Comparison of high-risk road section identification effects based on three velocity risk potential field intensities

同时间段内K2094+140～K2130+640路段事故总数为282起，空间速度风险势场强度最大值为297；K2064+140～K2094+140路段事故总数为157起，空间速度风险势场强度最大值为260.K2094+140～K2130+640路段的速度风险势场强度总体上大于K2064+140～K2094+140路段，与事故总量规律一致.对比有效性验证路段与实例分析路段相关统计数据，相关结果表明：1)速度风险势场强度和相关事故分布具有一定的规律性；2)3种速度风险势场对2处路段鉴别率均较高，选取的风险阈值能够对高速公路行车风险进行有效分类甄别；3)速度风险势场强度极值能够表征路段总体安全水平.综上所述，速度风险势场可以甄别不同形态的行车风险，能够量化描述高速公路行车风险的严重程度，与传统一维的鉴别方法相比实现了在二维空间上行车风险有效刻画.

5 结论

1）对路段和断面车速进行统计分析发现，同一时间段和同一路段内多数车辆速度趋近一致；同一断面处内、外侧车道的平均车速和车速离散度，随时间变化趋势基本一致；内、外侧车道平均速度比例基本一致.进一步分析发现速度梯度、道路半径、纵坡与交通事故分布具有一定的相关性.在此基础上，结合行车风险演化规律，提出了速度风险势场理论.

2）综合考虑道路线形和交通流速度，构建了速度势能和速度风险势场强度计算模型.以平面曲线半径和纵断面纵坡为指标，分别提出侧向和纵向风险影响因子计算方法.结合实际调研数据，对速度风险势场计算模型参数进行标定，给出了侧向分布系数φx的取值方法，引入速度变异系数提出速度风险势场强度系数η，同时考虑侧向、纵向和空间速度风险势场强度风险甄别间的不利情况，提出风险方向调整系数k的计算方法.

3）以西南山区某高速为实例进行速度风险势场计算，并与实际事故分布进行对比.有效性验证路段是当侧向、纵向和空间速度风险势场阈值为75.5、74.6和106.8时，甄别出的高风险路段占比分别为7.74%、12.88%、24.33%，路段涉及的对应事故占比分别为21.43%、34.21%、43.26%.结果显示风险甄别效果良好，侧向、纵向和空间速度风险势场甄别效益比分别为4.03、2.45、1.78.2处路段甄别结果证明速度风险势场均能有效评估路段行车风险，并且在一定程度上可以对高风险路段进行分类辨别.

4）提出速度风险势场理论及行车风险甄别方法，能够在二维空间上进一步实现风险路段定位、风险分类和量化，为宏观交通安全研究提供了新的方法.目前本研究所提出的风险阈值及确定方法，适用于宏观尺度的风险路段甄别，但是无法有效刻画车辆换道、超车等微观行车风险，具有一定局限性.此外，未考虑气象环境、车型比例、交通流密度等因素的影响，后续将进一步补充研究，以期实现宏观层面行车风险态势研判，提高高速公路安全管理的精准性和时效性.