基于XGBoost扩展金融因子的风电功率预测方法

王永生，关世杰，刘利民，高静，许志伟，刘广文

(1.内蒙古工业大学 数据科学与应用学院，内蒙古自治区 呼和浩特 010080；2.内蒙古自治区基于大数据的软件服务工程技术研究中心，内蒙古自治区 呼和浩特 010080；3.内蒙古农业大学 计算机与信息学院，内蒙古自治区 呼和浩特 010018)

随着世界经济的飞速发展，对于能源的需求也大幅提升，传统化石能源面临着枯竭的威胁.由于传统化石能源的大规模消耗而引起的气候变暖以及日益严重的环境污染问题，生态系统、社会经济以及人类健康均受到严重威胁[1]，大力发展风力发电、水力发电等可再生能源成为社会关注的重点.截至2021年底，我国风电并网装机容量突破3亿kW大关，相比于2016年底实现翻番，已经连续12年稳居全球第一.风力发电量占全社会用电量比例约7.5%，相比于2020年底提升1.3个%，风力发电对全国电力供应的贡献不断提升[2].由于风力、风向等自然气象条件的不确定性，使得风力发电具有较强的随机性与波动性，导致风力发电功率的预测工作受到影响.目前大多数预测方法依赖气象数据和专家经验，主要分为物理分析法、统计分析法以及二者相结合的方法[3].

物理分析法主要受数值天气预报(numerical weather prediction，NWP)及专家经验的影响.基于该方法的风力发电功率预测需要使用较多参数，如风速、风向、气压数据、地理地貌信息等，再依据风机功率特性曲线，计算输出功率.该方法具有不依赖历史数据的特点，但是模型复杂、计算量大、抗干扰能力弱，数值天气预报的精度和更新频率会影响预测精度和速度[4-6].Cheng等[7]提出将风电场涡轮机的实测风速同化到NWP数据中的预测方法，该方法提升了在孤立位置的风机输出功率预测准确率，降低了预测模型对NWP数据的依赖.

随着人工智能在各个领域的快速发展，基于人工智能的统计分析法被应用于风力发电功率预测领域.以机器学习或深度学习为基础的统计分析模型，由于实现误差反馈修正功能，使得功率预测模型具备容错转化能力，预测准确率得到显著提升[8].Ju等[9]将卷积神经网络与轻量梯度提升回归树算法(light gradient boosting machine, light-GBM)组合成一种新的预测模型，在中国西北部某风电场的数据集上，该方法取得良好的表现.Fu等[10]提出一种基于循环神经网络的新型多步超前风力发电预测模型，该模型在所提供的数据集中也获得良好的预测效果.

为了进一步提高预测准确率，近年出现统计分析法与物理分析法相结合的方法.Zhang等[11]将气象数据与风电场历史数据作为模型的输入，通过K-means进行聚类，最后每个集群构建带有注意力机制的模型(seqnence to sequerce, seq2Seq)，以进行风力发电功率预测.Sharifian等[12]提出一种基于 Type-2 模糊神经网络估计和基于种群的随机优化技术的新型智能方法以预测风力发电功率.该方法可以处理来自数据采集与监视控制系统（supervisory control and data acquisition, SCADA）数据、天气预报和测量工具参数的不确定性以提升模型预测准确率.实验表明，物理分析与统计分析相结合的预测方法可以进一步提升模型预测准确率.

在时间序列预测中，有大量的预测模型涌现.本研究根据现有的预测模型总结出2个问题：第1个问题是无论是15 min的超短期风力发电功率预测或是48 h以上的中长期的风力发电功率预测，模型训练需要2-3 h甚至更久，大多数模型难以在生产中实际应用；第2个问题在于现有数据过于单一，历史风电功率和气象数据难以表明时间序列的特征，一些不必要的气象数据也增加模型计算的负担和模型构建的时间成本.大多数现有预测模型并不能很好的应用于风电场，模型训练需要较高算力的GPU支持，大幅增加了风电场的营业成本.

Elsayed等[13]采用XGBoost算法，结合精心配置的数据，构造出媲美甚至超越深度学习的模型.XGBoost是由华盛顿大学的陈天奇博士提出的，该算法由梯度提升回归树(gradient boosting regression tree，GBRT)演化而来，最初惊艳于Kaggle竞赛，随后以出众的效率和较高的准确度得到广泛的应用.XGBoost算法是GBRT思想的实现，最大的特点是能够通过并行学习实现加速计算，同时在目标函数上加以改进来提高预测精度[14].神经网络在数据预测方面变得愈发流行， XGBoost算法在训练样本及训练时间有限的条件下，可以获得更好的预测效果.相比于深度神经网络，XGBoost能够更好的处理表格数据，并具有更强的可解释性.大量实验表明，该模型能在提升预测准确率的同时，使用最少的资源来解决问题[15].本研究拟通过使用XGBoost算法以解决第1个问题.通过对时间序列的观察，金融时间序列和风力发电时间序列具有一定相似性[16].在长达近150 a 的金融数据分析中，一些金融因子可以对金融趋势起到预测作用.在多种金融因子的协同作用下，金融趋势预测准确率明显提高.本研究拟通过将风力发电功率时间序列中衍生出的金融因子与原有时间序列中的时间窗口插入到原始风电功率数据集中，以解决第2个问题.

将风力发电功率时间序列衍生出的金融因子进行优化后并结合时间窗口插入到原有时间序列中，开展进一步数据分析.分析表明金融因子、时间窗口降低了对复杂神经网络以及气象数据的依赖性，因此对基于XGBoost扩展金融因子与时间窗口的超短期风电功率预测方法展开深入的研究.

1 模型构建与金融因子的计算方法

所提模型首先将二维时间序列数据转换为一维时间向量以构建时间窗口，根据一维时间向量绘制特有的风电功率K线，通过K线数据，计算出基于功率时序数据的随机指标（KDJ for power,KDJFP)与基于功率时序数据的移动异同平均数（MACD for power, MACDFP）的值并插入到原有数据集中，最后将改进后的数据集传入XGBoost中进行模型构建，并对风力发电功率进行预测，模型图如图1所示.

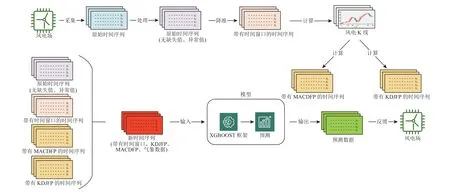
图1 基于XGBoost扩展金融因子的风电功率预测方法模型Fig.1 Model diagram of wind power prediction method based on XGBoost extended financial factor

1.1 时间窗口的构建

XGBoost算法根据每个特征值划分子叶并计算残差，当回归树达到最大深度或残差为0时停止树模型的构建.当预测时，最终根据每棵子树的判断加和得到结果.该方法中存在一个缺陷，即预测范围内的每个预测步骤都是独立预测的，模型无法从潜在关系中受益.因此，本研究构造了函数fdim，使得二维时间序列数据转换为一维时间向量，将潜在关系转化为时间窗口输入到模型中，以便模型捕捉到时间序列数据中变量的自相关效应.

对于时间序列数据集A，取x时刻时序数据值tx、x-1时刻时序数据值tx-1、x时刻与x-1时刻数据差值 ∇ (tx-1-tx)构成时间窗口.将时间窗口与x时刻的其余协变量ax、bx、cx组成新的时间序列数据集B，如式1所示.

式中：x+1为时刻数据值，tx+1为需要预测的数据值.

1.2 金融数据与时间序列数据的联系

金融市场中K线图的画法包含4个数据，即开盘价、最高价、最低价、收盘价，所有的K线都是围绕这4个数据展开.如图2所示，当收盘价高于开盘价时，则开盘价在下收盘价在上，使用空心长方柱表示；当收盘价低于开盘价时，则开盘价在上收盘价在下，使用实心长方柱表示.参照金融市场中的K线，根据风力发电功率数据(每15 min采样一次)，绘制风电K线图，绘制方法共分2个步骤.

第1步，按照每15 min采样一次数据的频率，将5个相邻采样点整合为一条数据; 第2步，将5个采样点中最大值视为金融市场中的最高价，将5个采样点中最小值视为金融市场中的最低价,将第一个采样点的功率输出值视为金融市场中的开盘价，将最后一个采样点的功率输出值视为金融市场中的收盘价.绘图结果如图2所示(图中P为功率，单位为MW；t为采集时间，单位为h)，同时风力发电功率K线图为24 h 制，即每天绘制24个长方柱(图2中以5 h为例).通过风力发电功率K线图，可以得到有关风力发电功率时间序列数据中的金融因子，以改进风力发电功率预测工作，进一步提高预测准确率.

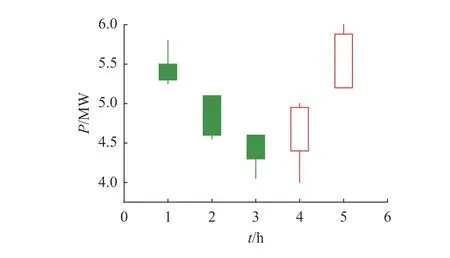
图2 风力发电功率K线图Fig.2 K-line diagram of wind power generation power

1.3 基于功率时序数据的随机指标

随机指标最早起源于期货市场，由于该指标由3种子指标构成，在金融市场中又被称为KDJ指标.KDJ指标最早是以KD指标的形式出现，而KD指标是在威廉指标的基础上发展起来的[17].本研究提出用于风力发电功率的KDJ方法，融合移动平均线的观念，形成比较准确的功率增降依据.KDJFP指标在设计过程中主要是研究功率输出最高值、最低值和采样结束值之间的关系，同时融合动量观念、强弱指标和移动平均线的一些优点.因此，可以比较迅速、直观的判断风力发电功率变化趋势.基于超短期的风力发电功率预测, 周期选择为3 h，相关算法1如下所示.

算法1基于风电时序数据的金融因子KDJFP算法输入：风力发电采样数据，其中将3 h结束时的功率值记为C3， 在3 h内最高功率值记为H3，在3 h内最低功率值记 为L3.

步骤：

1） RSV为未成熟随机值，第xh的RSV值为 R SVx.k为KDJ指标中的快速确认指标，第xh的k值为kx.d为KDJ指标中的慢速确认指标，第xh的d值为dx.j为KDJ指标中的趋势方向指标，第xh的j值为jx；

3）设kx-3为前3 h的k值，若不存在，使用50代替.使用步骤2所求的RSV，根据，计算出k值，k值的变化区间为0～100；

4）设dx-3为前3 h的d值，若不存在，使用50代替.使用步骤3所求的k，根据计算出d值，d值的变化区间为0～100；

5）使用步骤3所求k、步骤4所求d，根据jx=3kx-2dx，计算出j值；

end;输出：风电时序数据衍生出的金融因子KDJFP中的k值、d值、j值.

通过上述算法，在风力发电功率时间序列数据中，可以进一步提炼到更有价值的数据，以减少对自然气象数据的依赖.在实验部分，将展示KDJFP对预测准确度带来的积极影响.

1.4 基于功率时序数据的移动异同平均数

MACD(moving average convergence /divergence)是Geral Appel于1979年提出的，利用金融市场的短期指数移动平均线与长期指数移动平均线之间的聚合与分离状况，对金融趋势做出判断的技术指标[18].本研究提出用于风力发电功率的MACD方法，由快、慢均线的离散、聚合来表征当前的风力发电功率可能的发展变化趋势.MACDFP指标在设计过程中主要研究快速移动平均线与慢速移动平均线之间的关系，计算快速移动平均线与慢速移动平均线之间的离差值.通过对MACDFP和KDJFP的组合判断，可以进一步提升功率预测准确率.基于超短期的风力发电功率预测，快速移动平均线周期选择为3 h，慢速移动平均线周期选择 为5 h，相关算法2如下所示.

算法2基于风电时序数据的金融因子MACDFP算法输入：风力发电采样数据，其中将xh结束时的功率值记为Cx；

步骤：

3）设 D IFx为 第xh的差离值，使用步骤1中所求的 EMAfast与步骤2）中所求的 E MAslow，根 据DIFx=计 算 出D IFx值；

4）设DEAx为第xh的平滑移动平均值，使用步骤1中所求的 EMAfast与 步 骤2）中所求的EMAslow、根据计算出DEAx值；

end;输出： 风电时序数据衍生出的金融因子MACDFP中的DIF值、DEA值、MACD值.

通过本节与1.3节所提供的3种金融因子，可以得到一个更加丰富的数据集.在实验部分，将展示来自真实风电场的功率预测效果，以及功率变化趋势预测情况.

2 XGBoost算法

XGBoost是由多棵CART(classification and regression tree)组成，通过Gradient Tree Boosting实现多棵CART树的集成学习.在训练阶段中，每一棵决策树学习的是目标值与之前所有树预测值之和的残差.决策树构建过程会根据最优特征选择最优切分点，类似于平衡二叉树， 最终多棵决策树共同决策，将所有树的结果累加起来作为最终预测结果.

如图3所示，将数据传入模型中，模型根据训练集得到所需的若干棵CART树；将测试集的数据输入到所得的模型中，根据所有CART树的数据累加结果确定最终预测结果，其中t0为时间序列.假设输入数据(k=25，d=45，j=18，DIF=35, ···)，那么预测结果为1.582+0.566=2.148 MW.

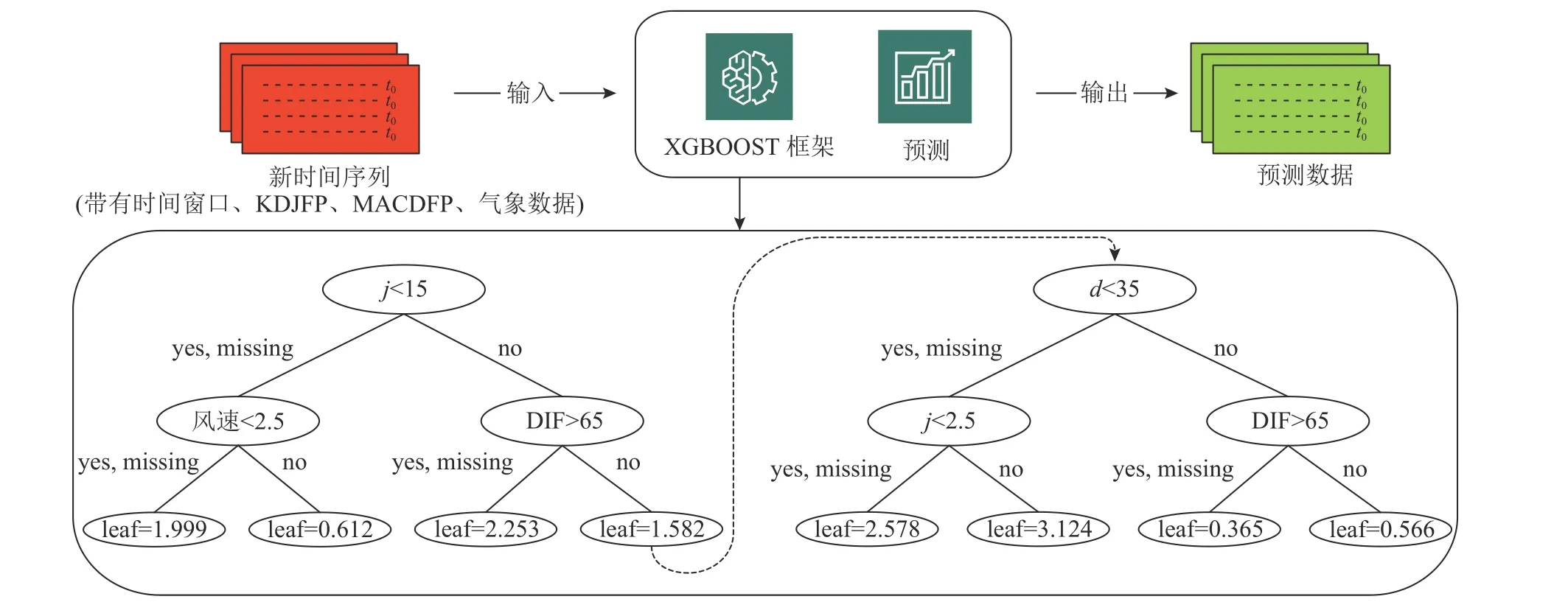
图3 XGBoost算法针对风电功率预测图Fig.3 XGBoost for wind power prediction diagram

综上所述并结合参考文献XGBoost模型定义[19-21]：

式中：目标函数Obj由2项组成，第1项为损失函数，用于评估模型预测值与真实值之间的误差.其中，l为模型损失函数，n为数据总数，i为数据序数，yi为第i条数据真实值，yˆi为 第i条数据预测值;第2项为正则化项，用来控制模型复杂度，避免过拟合.其中，r为树的总数，j为树的序数，fj为第j棵树，Ω为模型的正则化函数.在一般情况下，将损失函数的泰勒级数计算至二阶，并移除常数项，则有m棵CART树时，目标函数为

式中：gi与hi分别为一阶与二阶导数.

目标函数中的正则项定义为

式中：wj为树f中第j个子叶节点的分数；T为树f中叶子节点的总数目；γ 与λ为XGBoost的自定义参数，γ为L1正则的惩罚项，λ为L2正则的惩罚项.

第1项 γT通过叶子节点数及系数控制树的复杂度，从而抑制模型的复杂程度；第2项用于控制叶子节点的权重分数，以避免过拟合.此时目标函数为

式中：fm(xi)为 树模型，wj为叶子节点的权重，将二者统一，目标函数改写为

式中：Ij为叶子节点j的样本集，即落在叶子节点上的所有样本.fm(xi)将样本划分到叶子节点，计算得到该叶子节点的分数w，因此当i∈Ij时，可用wj替代fm(xi).

将式(6)视为一个自变量为wj，因变量为Obj的一元二次函数，根据最值公式，对于固定树结构，叶子节点j的最优为

因此，最优目标函数为

式中：Gj为叶子节点j样本集的一阶梯度统计，Gj=为叶子节点j样本集的二阶梯度统计，

3 实验设计与结果分析

使用XGBoost框架与Sklearn结合，通过numpy库、matplotlib库与pandas库实现风力发电功率K线绘制与KDJFP、MACDFP计算.预测结果准确性使用了平均绝对误差MAE、均方误差MSE、均方根误差RMSE、R2score等多种评判指标.在中国内蒙古某风电场的数据集中，采取消融实验以体现金融因子带来的积极影响，并在相同数据集的对比下，深度学习的预测结果表明XGBoost框架具有更高的准确率和更快的预测速度.在德国电力公司Tennet 2015—2020年风电功率数据集中，证实本研究所提模型具有较高的准确率和可移植性.

3.1 中国内蒙古某风电场风力发电功率数据

本研究通过中国内蒙古某风电场的数据进行训练和测试.其中原始数据包含2个部分：数值天气预报数据(numerical weather prediction，NWP)数据和风电场的功率数据.NWP数据由风电场于2019-1-1—2019-5-22以15 min的频率收集，并根据历史天气预报进行校正，NWP数据中有13493个条目.每个条目包括9个字段，日期和时间占据2个字段，气象特征(例如风速、风向、空气密度和大气压力)占据其他7个字段[22].

初步观测表明，数值天气预报数据质量较高，没有任何缺失值或异常值，这是因为这些数据收集于多个来源，并且经过了交叉检查.在功率数据中最重要的一列提供了实际的输出功率.在功率数据中，有68个时间点发现了空元素，562个时间点发现零元素，343个时间点发现异常元素(此处的异常是指气象条件正常，但输出功率远低于正常输出功率).这可能是SCADA故障或传输故障造成的[22]，因此在数据处理时，对缺失值与异常值采取删除措施.通过上述分析，将天气预报数据与功率数据进行拼接.在拼接后，时间和日期字段被转换为索引，不用于机器学习, 其他特征进行主成分分析.对输出功率影响不大的特征(例如海拔高度)进行删除，在12520个有效并且连续的条目中留下6个特征(风速、风向、温度、湿度、大气压力和空气密度).最后，获得了12520个有效条目，并转化为初始数据集.

3.1.1 评价标准 1）均方误差(mean square error，MSE)是模型在测试集中预测的值与真实值之间的平方误差平均值.对于同一数据集，MSE与预测效果呈负相关，计算公式为

式中：n为样本 数 量，yv与yˆv为样 本 的真实值与 预测值，v为样本序号.均方根误差(root mean square error，RMSE)是MSE的平方根，这2个指标含义相近.因为可以降低误差维数，RMSE更适合于计算与比较.MSE与RMSE均随样本数增加而增大，因此如果数据集不同，就不存在比较的意义.

2）平均绝对误差(mean absolute error，MAE)是测试集中预测值与真实值之间的平均绝对误差.MAE与预测效果呈负相关，该指标能准确反映实际预测误差，计算公式为

3）R2score MSE与RMSE在同一数据集下表现优异，使用多元化的指标从不同角度评价该模型的预测结果，因此引入了R2score衡量指标（R2）：

式中：为平均值.如果R2score＜0，则预测误差大于平均值的误差，代表当前模型毫无意义；如果R2=0，则预测值等于平均值，代表模型仍毫无意义；如果R2=1，则预测值等于真实值，代码模型可以进行无误差预测.因此，R2越接近1，预测模型越好.

4)准确率(accuracy rate，AR) 本研究拟定一个新指标以量化预测准确率：

3.1.2 实验设计 为了使XGBoost捕捉到数据中的潜在关系与自相关效应，模型将数据集中每个时间采集点的输出功率转化为窗口形式，取当前时间点前15 min的功率数据，当前时间点的功率数据构建时间窗口，并计算2个时间采集点之间的差值作为变化量.将这3类数据作为特征插入到原始数据集中，数据集特征数量增加至9个(15 min前功率值、当前功率值、变化量、风速、风向、温度、湿度、大气压力和空气密度)，数量为12519个有效条目.

为了进一步观察数据趋势，根据1.2节中的方法，最终获得了12515条K线.根据1.3、1.4节所提到方法，模型计算出KDJFP与MACDFP，并插入到数据集中.由于数据中的缺失值会使用定值代替，为了避免该代替方式给预测效果带来影响，在计算出KDJFP与MACDFP后，模型删除了前15条数据.数据集构建共有12500条数据，每条数据具有15个特征，分别是算法1中计算出的k、d、j，算法2中计算出的DIF、DEA、MACD值、15 min前功率、当前功率、变化量、风速、风向、湿度、温度、气压、空气密度.预测目标为当前时间点后15 min的输出功率，单位为MW.

将新数据集传入到XGBoost框架中，根据数据输入特征的不同，将实验分为7组进行.每组经过300轮次的训练后，对测试集中的数据进行测试，然后使用所提的5种评价指标和模型运行时间来判断模型优劣，最终取每组实验运行10次的平均值为最终结果.

3.1.3 实验结果 为了验证时间窗口和金融因子带来的积极影响进行多组实验，同时在相同数据集下对比本研究所提预测模型与深度学习预测模型的预测结果.在所有实验中，训练集占数据集80%，测试集占数据集20%.其中，气象条件指风速、风向、湿度、温度、气压、空气密度；时间窗口指15 min前功率、当前功率、变化量；金融因子指k、d、j、DIF、DEA、MACD.

第1组实验的输入数据特征为气象条件，共6个特征；第2组实验输入的数据特征为时间窗口，共3个特征；第3组实验输入的数据特征为金融因子，共6个特征; 第4组实验输入的数据特征为气象条件、时间窗口，共9个特征；第5组实验输入的数据特征为气象条件、金融因子，共12个特征；第6组实验输入的数据特征为气象条件、时间窗口、金融因子，共15个特征；第7组实验输入的数据特征为时间窗口、金融因子，共9个特征；第8组实验是本数据集在TSW-LSTM模型上进行的预测实验，它是由时间滑动窗口和长短期记忆网络所构成的深度学习模型[22].该模型是多个来源的风电数据进行融合，通过降维和标准化等操作进行清理，提取实际输出功率的循环特征，并通过时间滑动窗口算法(TSW)构建输入数据集.模型中所提的时间滑动窗口算法与本研究所提的时间窗口算法近似.在此基础上，建立TSW-LSTM预测模型，对风电场的超短期输出功率进行预测.

接下来将通过表1、2和图4来展示预测结果.表1中t1为训练时间，表2中特征重要性评分是该特征在所有梯度提升回归树中被作为分裂节点的次数；表中加粗的分数所对应的特征为当前组中最优特征，加下划线的分数所对应的特征为当前组中次优特征.在表2中，风速为V，风向为WDIR，湿度为HUM， 温度为T，气压为pa，密度为ρ，15min前功率为Po，当前功率为Pn，功率变化量为Pc.

在表1中，以组别1为基准实验，对比组别2与3，时间窗口与金融因子的加入使得MSE分别降低了55.88%与71.29%，同时准确率分别提升了5.61%与6.74%.在图4(图中P为功率，单位为MW；t为采集时间，单位为h)的(a)、(b)、(c)中可以看到，组别1的预测曲线与实际曲线吻合情况较差，组别2和3的预测曲线与实际曲线吻合情况明显提升.金融因子与时间窗口的加入，明显提升了风力发电功率预测的准确率.

在表1中，对比组别4和5可以发现，时间窗口和气象数据的混合模型预测准确率略高于金融因子和气象数据的混合模型，在图4 (d)、(e)中可以看到，2种模型的预测曲线与实际曲线吻合情况较好.组别6为金融因子、时间窗口、气象数据的混合模型，所有评价指标在7组组别中都是最高的，在图4的(f)中可以看到该模型预测曲线和实际曲线吻合良好，反映出组别6所构建的模型具有较高的预测精度.因此，认定组别6的模型是最佳模型.结合表1与图4的(f)、(g)，对比组别6、7可以发现，气象数据对于预测模型已经没有显著影响，可以将气象数据视为不必要的辅助信息删去以减少系统开销和模型训练时间.结合各评价指标判断，组别7的模型为高性价比模型.

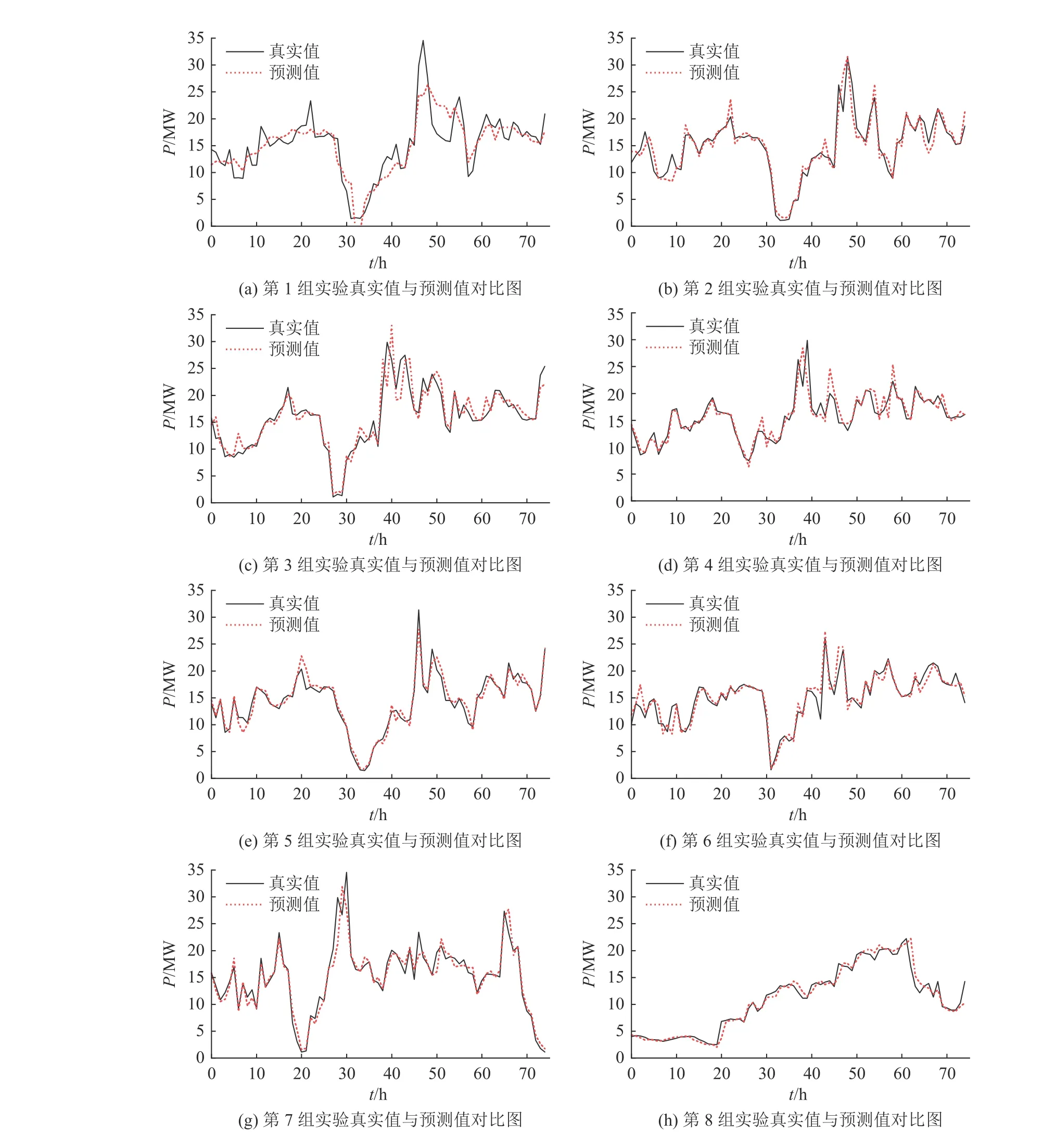
图4 基于XGBoost拓展金融因子的风电功率预测方法在中国内蒙古某风电场数据集上的预测效果Fig.4 Prediction effect of wind power prediction method based on XGBoost extended financial factor on wind farm data set in Inner Mongolia,China

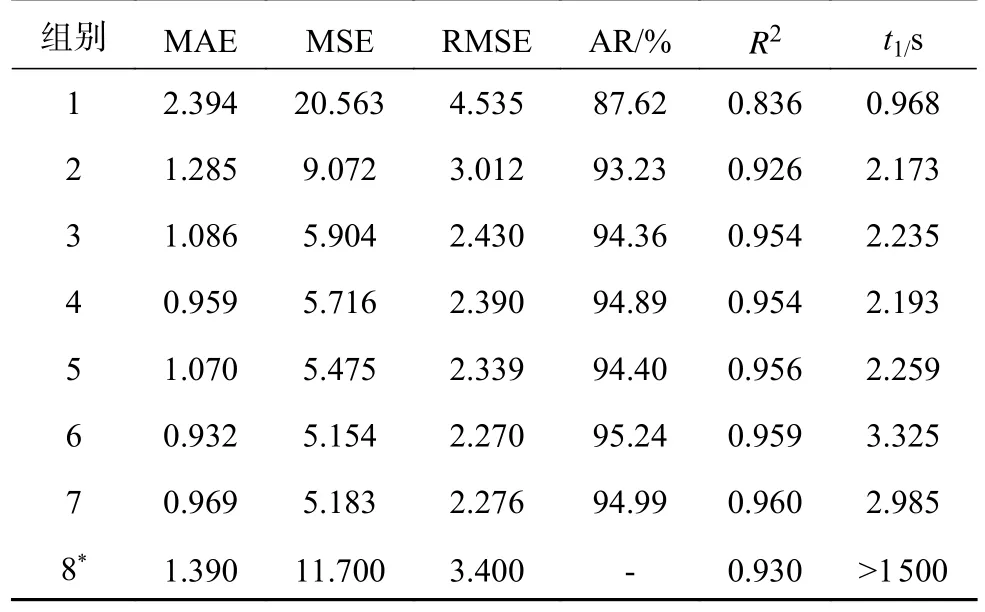
表1 基于XGBoost拓展金融因子的风电功率预测方法在中国内蒙古某风电场数据集上的实验结果Tab.1 Experimental results of wind power prediction method based on XGBoost extended financial factor on wind farm data set in Inner Mongolia, China

以组别1为基准实验，本研究所提最优模型提升约8.69%的准确率，MAE降低约61%，MSE降低约74.9%，RMSE降低约49.9%，R2提升约14.7%.对比组别8，本研究所提最优模型MAE降低约32.9%，MSE降低约55.9%，RMSE降低约33.2%，R2提升约3.1%，所以复杂的深度学习模型在相同数据集上的预测结果未能超过本研究所提的新模型.由此可见，基于XGBoost算法拓展金融因子的预测模型拥有着极高的训练精度，极短的训练时间，是一个可以媲美甚至超过深度学习的机器学习模型.

3.1.4 金融因子带来的积极影响 通过表2中组别4与5的特征重要性评分可知本研究所提的新模型中，时间窗口和金融因子的重要性远高于气象数据.组别5中气象数据重要性评分不及金融因子重要性评分的一半.组别6中总览所有特征，金融因子k位列第一名，其余金融因子的重要性均位居前列.接下来将展示另一个维度的评价标准，以进一步揭示金融因子带来的积极影响.

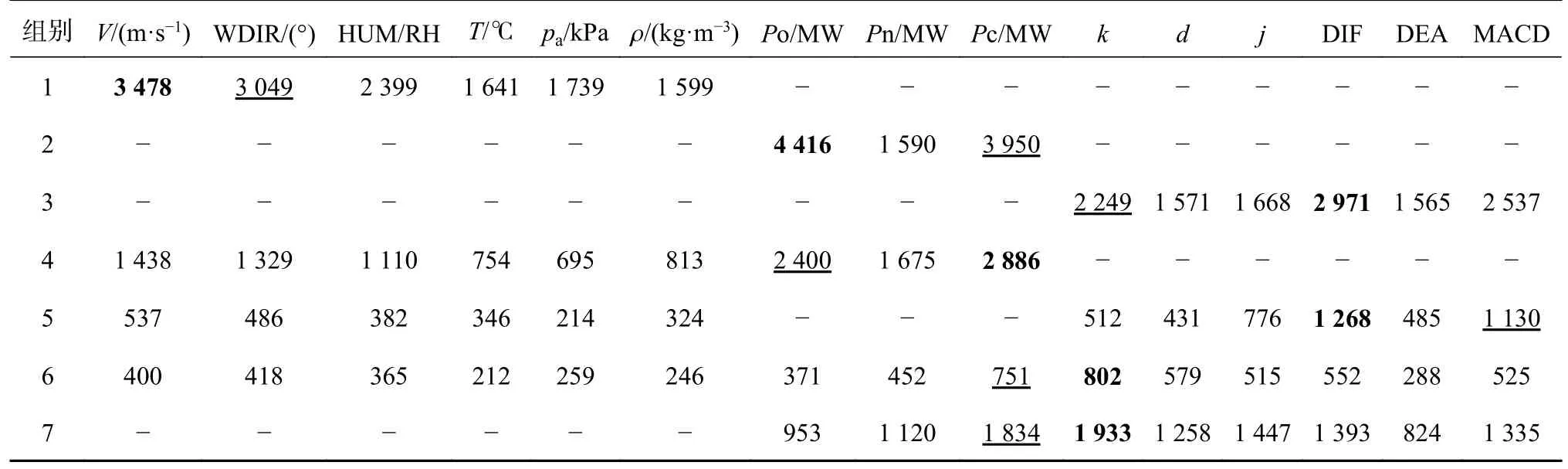
表2 中国内蒙古某风电场数据集中特征的重要性评分Tab.2 Importance scoring of features in data set of wind farm in Inner Mongolia, China

如图5所示，图中绘制K线的频次为每h一次，每天将绘制24个长方柱.当风电功率未出现明显下降趋势时，图5(b)中的金融因子j在第2条虚线处和第4条虚线处已经有明显下降趋势；图5(c)中的MACD_BAR值明显从正值变负值(空心柱体转换为实心柱体)，DIF与DEA已经呈现“死叉”现象(“死叉”为金融指标DIF下穿DEA的现象，一般出现此现象时，代表金融市场即将出现下降趋势).由此可以判断，风电功率即将进入下降趋势.后续数据显示，风力发电输出功率降幅达25%是在第2条虚线与第4条虚线之后，因此金融因子对于风力发电功率预测有明显作用.当图5(b)中的金融因子j风电功率未出现明显上升时，在第1条虚线处和第3条虚线处出现急升趋势；在图5(c)中，MACD_BAR值明显由负值变正值(实心柱体转换为空心柱体)，DIF与DEA已经呈现“金叉”现象(“金叉”为金融指标DIF上穿DEA的现象，一般出现此现象时，代表金融市场即将出现上升趋势).由此可以判断，风电功率即将出现上升趋势.后续数据显示,在第1条虚线后，风力发电输出功率增幅达25%；在第3条虚线后，风力发电输出功率增幅超过100%.综上所述，金融因子对于风力发电功率的预测起到至关重要的作用.

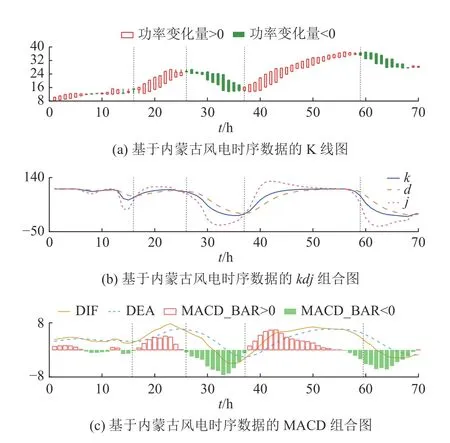
图5 风力发电功率综合K线图Fig.5 Wind power integrated K-line diagram

3.2 德国电力公司Tennet风力发电功率数据

Tennet是欧洲领先的电力传输系统运营商(TSO)，主要业务在荷兰和德国.通过ENTSO-E获取德国境内Tennet公司2015—2020年短期风力发电功率数据，其中包括陆地风力发电功率数据集以及海洋风力发电功率数据集.本实验在2个数据集上进行模型的构建与未来功率预测.

3.2.1 数据处理方案 由于陆地风力发电功率数据集和海洋风力发电功率数据集大小和维度一致，因此以下处理方案在2个数据集中均适用.ENTSO-E披露自2015-1-100:00—2020-9-3023:45的风力发电情况，原始数据中共包含201600条数据，不包括气象数据及其它因素，仅含有每15 min的功率值.功率数据是该公司在德国所有风电设备输出功率总和，因此不存在空值及异常值问题，无需进行特殊处理.

按照1.1、1.2、1.3、1.4所提的处理方法，模型重新构建数据集，最终该数据集包含200000条数据，每条数据含有9个特征：k、d、j、DIF、DEA、MACD、前15 min数据、当前数据、变化量.预测目标为当前时间点后15 min的输出功率，单位为102MW.

3.2.2 实验设计 由于数据集包含20余万条数据，模型部分参数进行小幅调整，将训练轮次降低为150轮.评价指标同3.1.1中所设计的评价指标，其余实验设置及方法同3.1.2中所提到的方法.最终取每组实验运行10次的平均值为最终结果.

3.2.3 实验结果 为了验证所提模型具有较好的可移植性进行2组实验，分别是陆地风力发电功率预测实验和海洋风力发电功率预测实验.训练集占数据集中的80%，测试集占数据集中的20%.第1组实验的输入数据为陆地风力发电数据，包含全部特征; 第2组实验的输入数据为海洋风力发电数据，包含全部特征.

通过表3和图6(纵轴功率p的单位为102MW)，时间窗口与金融因子对预测所带来的积极影响进一步被证实.数据集是Tennet公司在德国全境的风力发电数据，所以不存在缺失值与异常值，受风机故障或局部地区环境影响的可能性大幅降低，本研究在大型数据集上拥有更高的预测准确率.

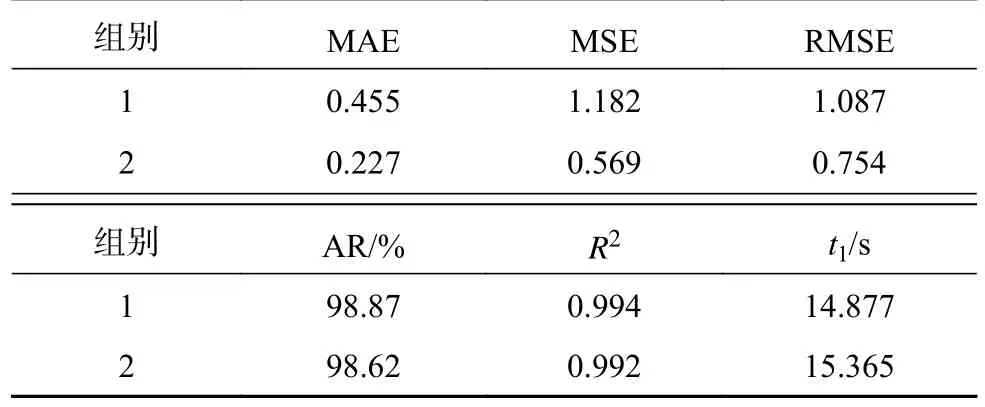
表3 基于XGBoost拓展金融因子的风电功率预测方法在德国Tennet公司风电数据集上的实验结果Tab.3 Experimental results of wind power prediction method based on XGBoost extended financial factor on German Tennet wind power data set

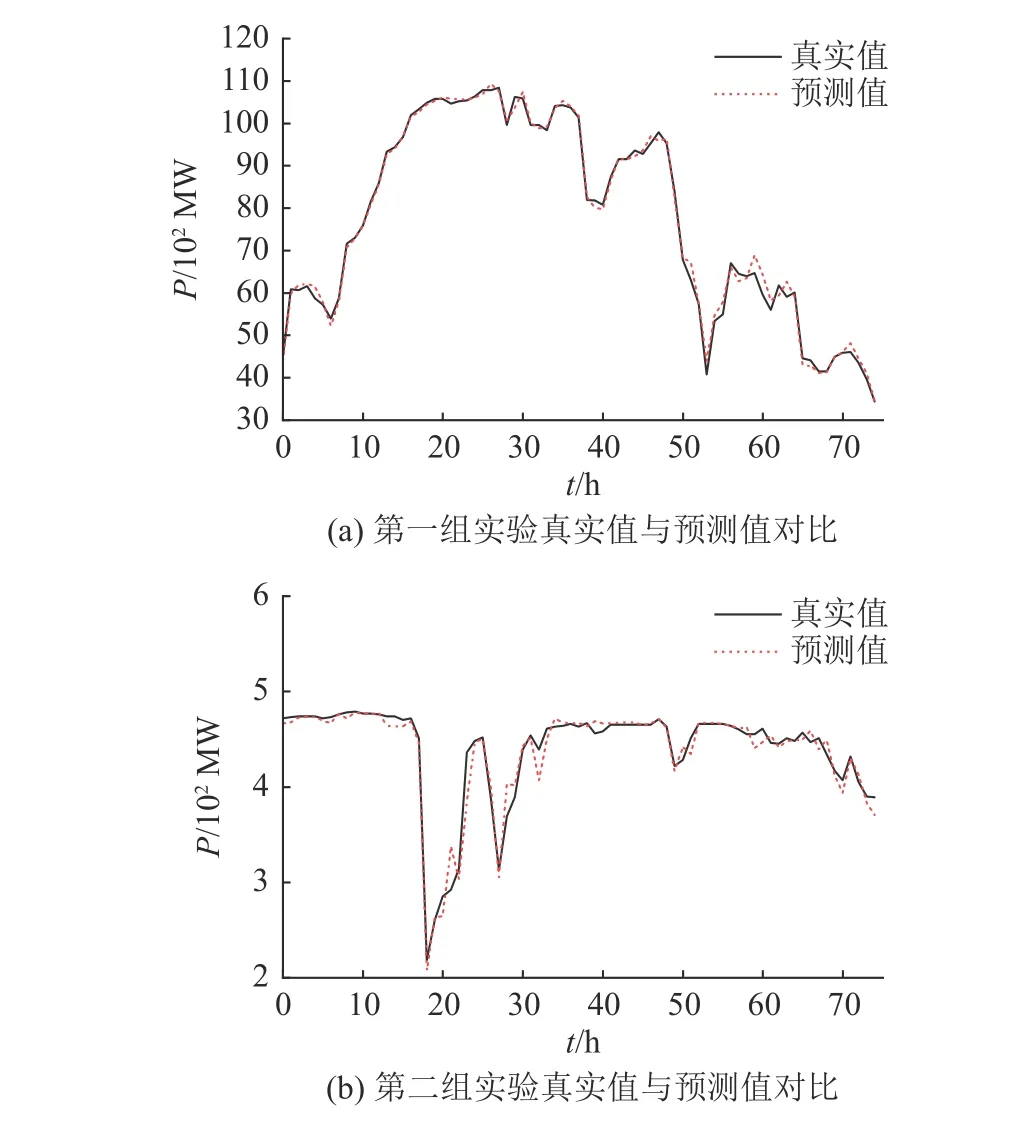
图6 基于XGBoost拓展金融因子的风电功率预测方法在德国Tennet公司风电数据集上的预测效果Fig.6 Prediction effect of wind power prediction method based on XGBoost extended financial factor on German Tennet wind power data set

4 结语

本研究提出一种基于XGBoost扩展金融因子的风力发电功率预测方法，分别使用中国内蒙古某风电场数据集和德国电力公司Tennet风力发电功率数据集进行模型训练和数据预测.主要结论如下.

1) 本研究所提的数据处理方式可以增加数据维度，在风力发电功率预测中可以降低对气象数据和高精度模型的依赖.

2) 在时间序列数据中加入时间窗口和金融因子能够大幅提升未来数据预测准确率.

3) 基于XGBoost扩展金融因子的风电功率预测方法的准确率可以媲美甚至超过深度学习模型，同时得益于它较快训练速度，可以将模型部署至生产环境中使用.

4) 数据集中的缺失值和异常值会对金融因子的计算产生一定误差，从而无法得到理想的预测结果.一个地域或一个集群所产生的数据中，缺失值和异常值所带来的影响会大大降低.在大规模的数据集中本研究所提出的预测模型拥有更高的预测准确率.

本研究对于缺失数据的处理仍有不足，计划在下一步研究计划中，对缺失值、异常值进行误差修正研究，进一步提升预测效果，使模型趋于完善，推动其更好地应用于风电场.