大跨钢-混凝土组合楼盖的优化设计

吴一凡，潘文豪，罗尧治

(1.浙江大学空间结构研究中心，浙江 杭州 310058；2.浙江大学平衡建筑研究中心，浙江 杭州 310028；3.浙江大学建筑设计研究院有限公司，浙江 杭州 310028；4.浙江省空间结构重点实验室，浙江 杭州 310058)

随着现代社会经济和文化事业的不断进步，建筑的功能逐渐有了多元化发展.传统大跨建筑结构主要为屋盖结构，通常仅有一层大空间，在 工业厂房、交通枢纽和体育场馆中，多层大空间建筑日益增多.因此，大跨楼盖结构的需求有了极大的增加.钢-混凝土组合楼盖已经被广泛应用于多高层建筑的中大跨楼盖结构中.通过发挥组合作用，钢-混凝土组合结构可取得节省材料、减轻自重、缩短施工工期、增大使用空间、提升人居品质等综合优势.从2000年左右开始，清华大学聂建国教授研究团队[1-5]对钢-混凝土组合楼盖开展长期的研究工作.该团队发明或发展了多种新型大跨组合楼盖结构，其中包括双向钢-混凝土组合楼盖（可采用现浇楼板或叠合楼板的形式）、单双向混合组合楼盖和异形斜交组合楼盖.这些成果成功应用于武昌火车站、山东滨州会展中心、苏州吴江大厦等大型工程建设项目.贵州大学马克俭教授团队[6-8]对大跨度钢-混凝土空间网格组合楼盖进行了大量的研究与创新工作，提出钢-混凝土组合空腹夹层板楼盖、H型钢空间网格组合楼盖、蜂窝型钢混组合空腹夹层板楼盖等多种大跨度空间组合楼盖体系.研究成果在贵州省博物馆、黑龙江中医药大学文体中心、湖南九华创新园等多个工程项目中得到应用.

为了实现组合楼盖的经济效益最大化，考虑大跨单向钢-混凝土组合楼盖的优化研究.针对钢-混凝土组合楼盖的优化问题，已有许多研究运用不同的算法做大量研究与比较，如和声搜索算法[9]、狩猎搜索算法[10]、非线性规划法[11]、遗传算法[12]、蚁群算法[13]、改进蚁群算法[14]、粒子群算法[15]等.此类研究工作倾向于关注算法的迭代次数、求解效率等指标，通常利用案例分析展现算法在优化计算和节约成本方面的高效性.Kaveh等[16]比较分析各类和声搜索算法的计算性能，Korouzhdeh等[14,17]在文献[16]案例分析数据的基础上，继续比较和声搜索算法、蚁群算法、改进蚁群算法和广义简约梯度法的优劣性.Ebid[17]的研究表明，广义简约梯度法收敛性好，进行组合楼盖的优化分析时表现较佳.

在优化算法的基础上，研究人员还进行了参数分析，主要目的是研究各参数对组合楼盖经济性的影响.常见的分析参数为组合楼盖的跨度和所受荷载.Kaveh等[13]和Korouzhdeh等[14]分别采用蚁群算法和改进蚁群算法对组合楼盖进行参数分析，研究3组可变荷载（可变荷载最大为3 kN/m2）下，4个不同跨度（最大跨度为8 m）的组合楼盖之间的成本差异，获得不同荷载下组合楼盖用钢量随跨度的变化关系.Senouci等[12]进行类似的案例研究和参数分析，参数分析的最大可变荷载为16.33 kN/m2，最大跨度为10 m.为了研究大跨度组合楼盖的优化设计问题，研究人员扩大参数研究范围，使得范围符合大跨度组合楼盖的应用工况.Kravanja等[18]、Klanšek等[19-20]和Kravanja等[21]分别研究可变荷载2 ～10 kN/m2、跨度小于50 m的大跨度钢-混凝土组合楼盖的优化设计问题，还对不同截面形式的组合楼盖的优势跨度和经济性进行比较分析，研究结果表明焊接工字钢组合楼盖经济适用范围广，并且在大跨度、大荷载情况下表现优异.

从基于算法的案例研究到参数分析，组合楼盖优化设计研究逐渐向大荷载、大跨度方向发展，符合组合楼盖的发展方向和应用实景.对于超大跨度下钢-混凝土组合楼盖的适用性问题的分析与探讨仍较缺乏.目前参数分析的组合楼盖截面基本采用双轴对称的焊接或轧制工字形钢，经济性更好的单轴对称焊接工字钢截面的研究不足.此外，一些研究者在组合楼盖的优化研究中，忽视部分重要的变量或约束条件.对于组合楼盖而言，全面考虑变量和约束的设置十分必要，一些重要的变量和约束条件能够起到对截面尺寸和总用钢量的调节作用，由此影响组合楼盖的经济性.许多已有的研究未将混凝土翼板厚度、组合梁间距、钢梁截面的高厚比限值、组合截面的塑性中和轴位置等变量或约束纳入考虑，因此存在一定的局限性.

考虑到现有研究的上述不足，本研究进行单向钢-混凝土组合楼盖的优化设计，以探究该形式组合楼盖的适用范围和优化设计方向.以国内工程中常用的混凝土与钢材组成的组合楼盖为对象进行研究，采用塑性分析方法研究组合梁的极限弯矩，同时考虑塑性中和轴的位置.优化目标函数为组合楼盖的经济等效用钢量，与混凝土、钢材的价格和用量有关，反映组合楼盖等效的钢材消耗程度.采用广义简约梯度算法，全面考虑优化变量和约束条件，变量包括焊接工字钢的尺寸、钢梁间距和混凝土翼板厚度等8个参数，约束设置时参考规范规定和工程经验.根据优化结果，从跨度和荷载角度分析钢-混凝土组合楼盖的经济性和适用范围，探讨超大跨度下组合梁截面的发展趋势，并以此为基础提出组合楼盖体系的发展展望.

1 问题定义

考虑如图1所示的简支单跨钢-混凝土组合楼盖的优化设计问题，钢梁截面采用焊接工字形钢.本设计研究的跨度范围L= 10～100 m，可变荷载的范围为ω=2～10 kN/m2，永久荷载取结构自重.组合楼盖的材料特性和配筋如下：

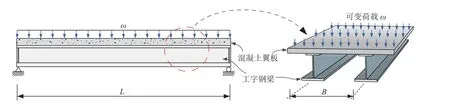
图1 组合楼盖优化模型示意图Fig.1 Optimization model of composite floor system

1）考虑楼板结构常用的C35混凝土，抗压强度设计值fc= 16.7 MPa；钢材采用Q355b，屈服强度fy= 355 MPa，强度设计值f= 305 MPa.混凝土容重ρc= 25 kN/m3，钢材容重ρs= 78.5 kN/m3.

2）混凝土板配筋采用双层双向钢筋网，板底受力筋取经济配筋率为0.6%，板底纵向钢筋和板顶双向钢筋按分布钢筋考虑，取构造配筋率为0.2%.

在一定跨度L和可变荷载ω条件下，优化设计的目标是通过变化钢梁和混凝土板的设计参数，求解满足国家规范等实际设计要求的等效用钢量最经济的楼盖组合梁截面.

2 优化方法与实现

2.1 计算假定

组合梁优化设计时根据钢结构设计标准[22]采用塑性分析方法，计算截面如图2所示，采用以下计算假定.

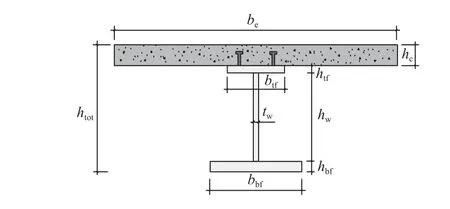
图2 组合梁计算截面示意图Fig.2 Cross-section of composite beam for calculation

1）混凝土翼板和钢梁之间为完全抗剪连接，不考虑两者之间的滑移.

2）受拉区的混凝土由于开裂不参加工作.

3）受压区混凝土均匀受压，且达到混凝土抗压强度设计值fc；钢梁在受拉区均匀受拉，在受压区均匀受压，并分别达到钢材抗拉、抗压强度的设计值f.

4）组合梁截面的混凝土翼板的计算宽度be按混凝土结构设计规范[23]计算：

式中：l为组合梁跨度，B为钢梁间距.

在图2中，be为混凝土翼板计算宽度，hc为混凝翼板厚度；htf、btf为钢梁上翼缘厚度、宽度；hbf、bbf为钢梁下翼缘厚度、宽度；hw、tw为腹板高度 、厚度；htot为组合梁的总高度，htot=hc+htf+hw+hbf.

2.2 优化方法

本优化问题需要求解满足在实际工程设计要求的约束限制下，使得参数分析经济等效用钢量最小的钢-混凝土组合楼盖的截面设计参数.

2.2.1 目标函数 根据优化目标，选取塑性分析下组合梁截面的经济等效用钢量W为目标函数，有

式中：W为经济等效用钢量，含义为单位楼盖面积上的等效钢材用量；As为钢梁截面面积；Ac为混凝土翼板面积，Ac=hc×B；ρ为混凝土翼板的总配 筋 率，ρ =0.6%+0.2%+0.2%+0.2%=1.2% ；α为混凝土单价与钢材等体积单价之比.本研究将优化问题中混凝土的单价取为500 元/m3[24]，钢材价格取为6000元/吨[25]，α按式(3)计算：

2.2.2 优化变量 优化变量包括钢梁间距B、混凝土翼板厚度hc，钢梁上翼缘厚度htf、上翼缘宽度btf，钢梁下翼缘厚度hbf、下翼缘宽度bbf，腹板高度hw、腹板厚度tw共8个参数.

2.2.3 约束条件 本优化问题的约束条件全面考虑塑性设计要求、规范规定和工程经验，设置如下：

a）组合梁的正弯矩设计值M小于截面极限抗弯承载力设计值Mu，即

1）塑性中和轴位于混凝土翼板截面（Asf≤behcfc）：

式中：xc为混凝土翼板受压区高度，xc=Asf/befc.

2）塑性中和轴位于钢梁上翼缘截面（Asf-2btfhtff≤behcfc＜Asf）：

式中：xtf为钢梁上翼缘受压区高度

3）塑性中和轴位于钢梁腹板截面（Asf-2btfhtff-2hwtwf≤behcfc＜Asf-2btfhtff）：

式中：xw为钢梁腹板受压区高度，xw=

b）钢梁的翼缘满足塑性设计下的宽厚比要求即

式中：b为翼缘外伸长度，t为翼缘厚度.

c）钢梁的腹板满足塑性设计下的高厚比要求，对该简支梁模型有

d）钢梁上翼缘面积比钢梁下翼缘面积不宜过小，本研究取如下约束：

e）钢梁间距和混凝土翼板厚度应考虑工程实际，本研究取如下约束：

f）组合梁总高度通过经济高跨比[3,26]限制：

g）组合梁抗剪、挠度等其他约束.

2.3 程序实现

采用广义简约梯度法对组合梁截面模型进行优化分析.此算法的求解方式是沿目标函数的梯度下降方向搜索满足约束条件的可行点，当目标函数的梯度为0时，判断达到最优解.程序实现有多种途径，采用Solver SDK优化分析工具，借助Matlab实现.该优化分析工具搭载系列规划求解引擎，可以解决许多非线性优化问题.在给定约束的限制下，程序通过对变量的组合分析，实现指定目标函数达到最小值，同时输出该最优情况下的相应变量值.在截面的优化分析过程中，考虑到最优截面的塑性中和轴位置并非确定，塑性中和轴位置不同时的约束条件和正弯矩承载力计算公式也有所不同，故求解时按照塑性中和轴位于混凝土翼板截面内、钢梁上翼缘截面内、钢梁腹板截面内3种情况进行比较寻优.

3 优化结果

3.1 组合楼盖的经济等效用钢量

通过对优化结果的汇总与处理，得到跨度L和可变荷载ω这2个设计参数下组合楼盖的经济等效用钢量的变化曲面，如图3所示.组合楼盖的经济等效用钢量随跨度的增大而增大，并且随可变荷载的增大而增大.当跨度和可变荷载同时增大时，经济等效用钢量指标迅速增大，指向不经济的设计工况.由图3可见，组合楼盖的经济等效用钢量在跨度和可变荷载2个设计参数的影响下变化明显.

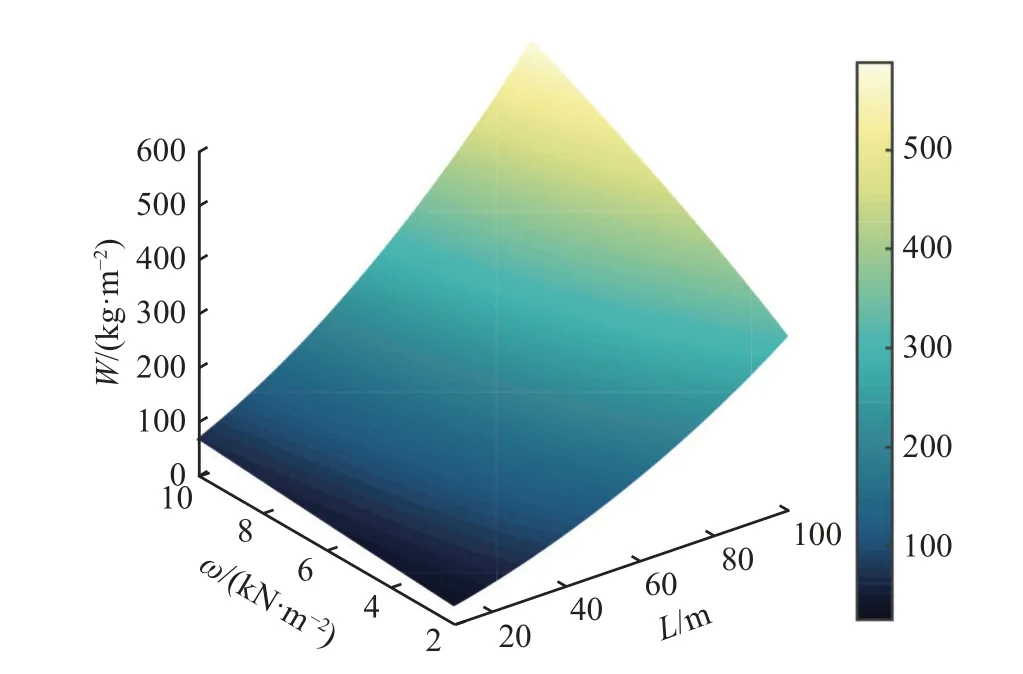
图3 组合楼盖的经济等效用钢量图Fig.3 Graphic diagram of economical equivalent steel consumption of composite floor

对用钢量三维图进行投影处理，可以得到经济等效用钢量的等值线图，如图4所示，其中等值线上数值的单位为kg/m2.由图可见，用钢量等值线在组合梁跨度和可变荷载的共同影响下呈内凹的形状，随着跨度和荷载的增大呈现出由疏向密的分布特性.以可变荷载为4 kN/m2时为例，经济等效用钢量为50、100、150和200 kg/m2对应的组合梁跨度分别为22、40、54和65 m.每增加50 kg/m2的用钢量，容许的跨度增量从18、14到11 m不断减小.从60～70 m开始，增加50 kg/m2用钢量获得的容许跨度增量不足10 m，若同时考虑等值线分布较密的可变荷载大于6 kN/m2的工况，则跨度的增量更为有限.随着跨度的增加，增大用钢量对提升组合楼盖容许跨度的效果逐渐减弱.在跨度大于60～70 m、可变荷载大于6 kN/m2时，仍采用传统组合楼盖的设计可能导致经济性降低.

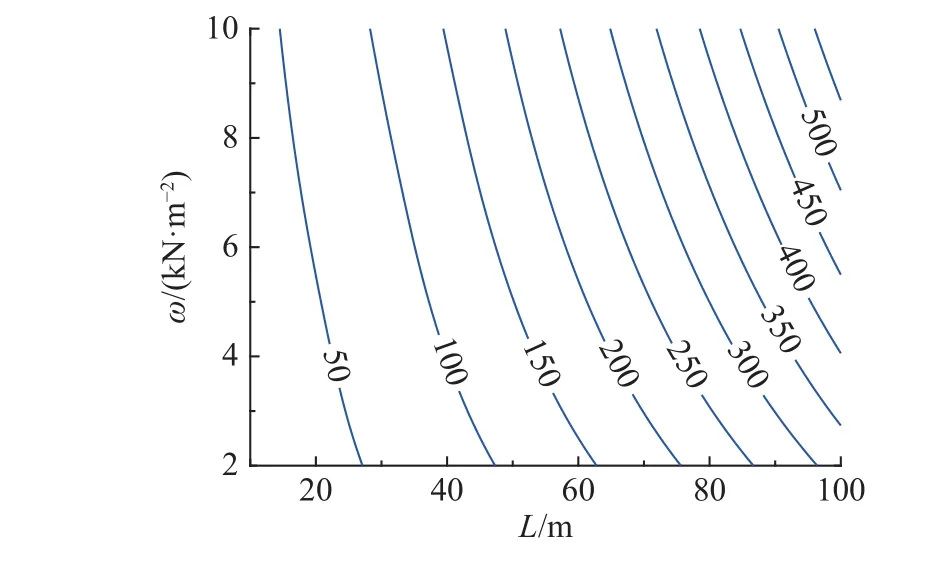
图4 组合楼盖经济等效用钢量等值线图Fig.4 Isolines of economical equivalent steel consumption of composite floor

取可变荷载为2、4、6和8 kN/m2这4种工况，图5（a）为组合楼盖的经济等效用钢量随跨度的变化情况.合楼盖的经济等效用钢量曲线随着跨度增大明显上升，特别是在跨度大于60～70 m后，等效用钢量迅速增加.为了考察用钢量随跨度的变化速率，图5（b）给出用钢量增加速率U与跨度的关系曲线.随跨度的增加，组合楼盖等效用钢量的增加速率也越快.同时考虑到可变荷载的影响，荷载越大，等效用钢量增速越快.当跨度和可变荷载均很大时，大跨楼盖结构采用钢-混凝土组合楼盖的设计方案导致楼盖的经济性逐渐减弱.

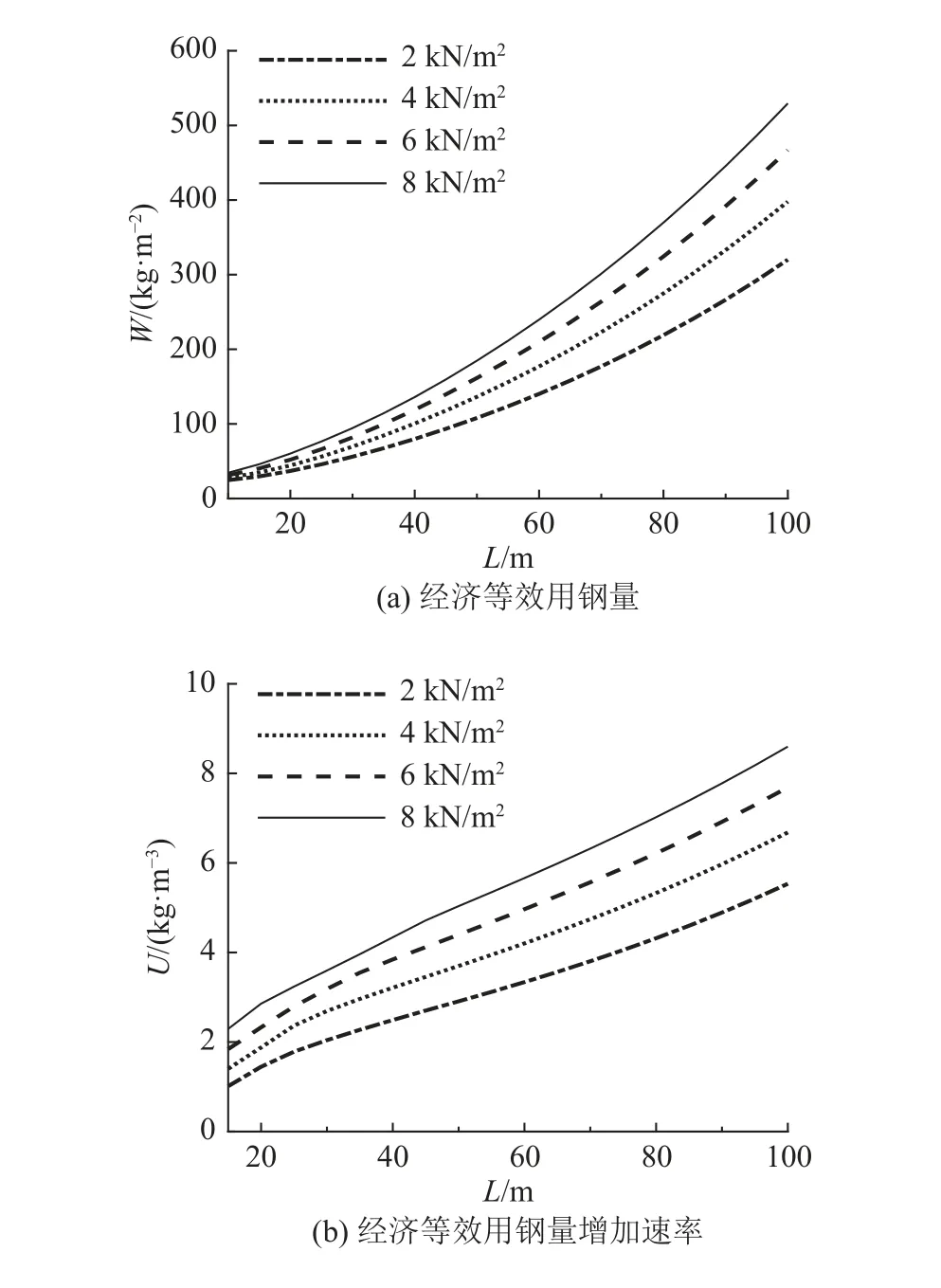
图5 组合楼盖经济等效用钢量变化趋势Fig.5 Variations and trends of economical equivalent steel consumption of composite floor

3.2 截面优化结果

优化程序同时给出各工况下最经济的截面优化结果.结果表明，钢-混凝土组合楼盖的最优钢梁截面宜采用上翼缘较小的单轴对称焊接工字钢，以充分发挥下翼缘的抗弯承载效率.楼盖组合梁最优截面恰好达到塑性设计的宽厚比与高厚比限值、梁高限值以及钢梁上翼缘与下翼缘面积比的限值.

根据优化结果，当跨度和可变荷载增大时，楼盖的优化组合梁截面所需钢梁也不断增大.为了探究优化截面的钢梁形态，考虑到优化截面的腹板面积与钢梁总面积之比Ra，绘制出可变荷载为4 kN/m2和6 kN/m2这2种工况下Ra随组合楼盖跨度的变化曲线，如图6所示.组合楼盖优化截面的腹板与钢梁面积比随跨度增大而迅速增大，当跨度大于30 m左右后面积比保持在0.6～0.7.在超大跨度需求时继续采用钢-混凝土组合楼盖设计，腹板面积占钢梁截面的比例增大，考虑到腹板对抗弯承载力的贡献相对翼缘效率更低，因此超大跨度下传统组合楼盖的经济性下降.

图6 优化截面腹板面积与钢梁总面积比Fig.6 Ratios between area of optimized cross-section’s steel web and whole steel section

优化组合梁截面的塑性中和轴位置反映出一定的截面特性.根据优化结果，计算出塑性中和轴离混凝土和钢梁交界面的距离（其中混凝土向为正，钢梁向为负）与总梁高的比值，用Rh表示，绘制出Rh随跨度的变化曲线，如图7所示.当跨度为10 m时，组合梁最优截面所需钢梁小，中和轴在混凝土板内.从跨度约15 m开始，组合梁最优截面的中和轴开始进入钢梁，为了充分发挥抗弯性能，最优截面的中和轴位置随跨度的增加快速向钢梁中部靠近，因此图7前段的中和轴位置呈现出迅速下移的变化特点.从约40 m跨度开始，中和轴位置变化速度减缓，60 m后中和轴位置基本不变.这说明对于超大跨度组合楼盖，优化的组合梁截面受力特点与纯钢梁更相近，此时优化的组合截面已经不能充分发挥钢-混凝土组合结构的组合作用，楼盖的经济性降低，需要考虑其他的楼盖跨越形式.

图7 优化截面塑性中和轴位置图Fig.7 Positions of plastic neutral axis of optimized composite crosssection

3.3 组合楼盖经济性的探讨与发展展望

超大跨度下钢-混凝土组合楼盖经济性下降的原因与截面组成关系密切，图8反映不同可变荷载下组合楼盖所承受荷载的占比r的分布情况.由图可知，组合梁截面的结构自重随跨度的增加逐渐增大，其中混凝土自重占比逐渐减小，而钢梁自重的占比快速增加，逐渐成为结构自重的主要组成部分.对于普通跨度的组合梁截面，优化得到的截面能较好发挥钢-混凝土组合楼盖的组合作用，随着跨度增加，组合作用不断减弱，组合楼盖的经济性也逐渐下降；对于超大跨度下的组合梁截面，优化显示的组合截面性质更接近纯钢梁，这样的截面已经无法高效发挥组合楼盖的组合作用，因此经济性降低.

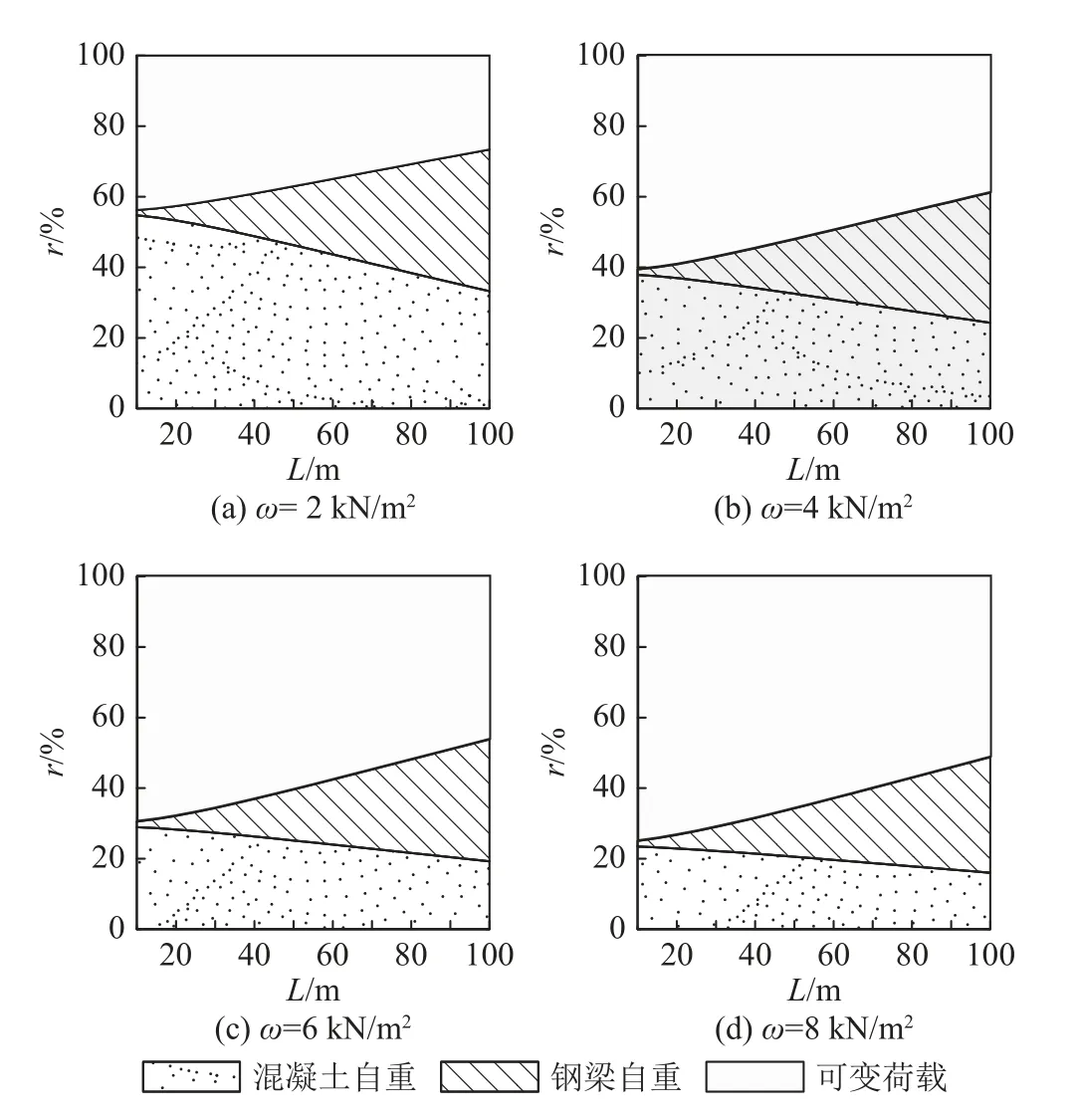
图8 组合楼盖承受荷载占比Fig.8 Proportions of imposed loads of composite floor

这一现象的出现主要归因于目前典型的组合楼盖仍采用传统的工字形钢梁.当楼盖的组合梁截面总高度为优化梁高htot=L/20时，随着跨度增大，楼板厚度变化相较钢梁梁高的变化很小，因此钢梁梁高占比不断增大.当梁高很高时，腹板的尺寸往往由高厚比确定，而不由抗剪承载力确定.因此，在大跨度需求时继续采用传统组合楼盖设计，由于腹板高厚比的限制，抗弯承载效率相对较低的腹板占钢梁截面的比例迅速增大，导致大跨度组合楼盖的经济性下降.

为了进一步拓宽组合楼盖的适用范围，需要开发新的组合梁体系.解决思路是从抗弯承载效率相对较低的腹板着手，通过降低腹板区域的用钢比例达到减小用钢量、提高承载效率的目的.波形钢腹板组合梁（图9(a)）已在更大跨的组合结构中得到使用[27].波形钢板具有抗剪承载力高、稳定性好的优点，此外还有轴向刚度小的特点.利用波形钢板优异的抗剪承载力和稳定性，波形钢腹板组合梁截面的腹板高厚比限值大幅增加，从而可有效地减小抗弯承载效率相对较低的腹板的用钢量；利用波形钢板轴向刚度小的特点，波形钢腹板组合梁截面实现抗弯抗剪的受力分离，其中抗弯由钢梁的翼缘与混凝土板承担，抗剪由腹板承担，承载效率显著增大.图9（b）为聂建国等[28]提出的各类新型波形钢腹板组合梁形式，将波形钢腹板组合梁在大跨组合结构中推广应用，具有良好的经济效益.

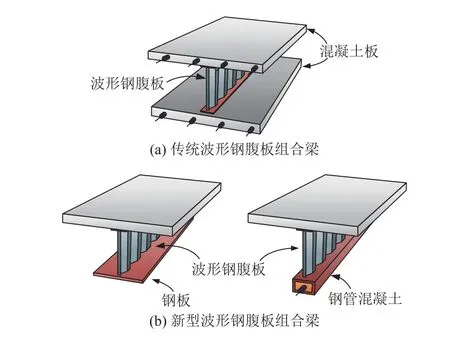
图9 波形钢腹板组合梁Fig.9 Composite beam with corrugated web

从空间结构的角度出发，研究人员[29-30]开始采用张弦梁结构体系.对于大跨结构设计，张弦梁结构传力效率高、跨越能力强，是一种常用的结构形式[31-32].图10为张弦梁结构的受力概念分析，通过拉索内的轴拉力和主梁内的轴压力形成力偶，高效地抵抗竖向荷载.张弦梁结构体系简洁美观、形式多样，在大跨屋盖结构中应用取得了显著的社会经济效益.

图10 张弦梁结构的受力概念分析Fig.10 Mechanical analysis of cable-supported beam

为了进一步提升传统钢-混凝土组合楼盖结构的适用跨度，张弦梁体系已经开始用于大跨组合楼盖结构中[33].相对于屋盖结构，大跨楼盖结构的竖向荷载显著增大.考虑到楼盖结构该特点，张弦梁用于超大跨楼盖结构体系的经济设计，关键是在受轴压力的主梁截面中采用混凝土材料，即采用钢-混凝土组合的主梁截面，如图11所示.图11（b）为传统工字钢-混凝土组合主梁的截面，具有构造简单、施工方便等优点.图11（c）为本研究提出适用于弦支组合梁的另一种主梁截面形式，采用钢管混凝土-混凝土板组合主梁.相比较传统主梁截面，钢管混凝土-混凝土板组合梁的截面抵抗轴压和负弯矩作用的性能得到极大增强.图11（c）所示的新型弦支组合梁可以避免预应力态下工字钢主梁的稳定问题，同时在该弦支组合梁的设计中，可以采用更大的拉索截面积和初始预应力，显著提升弦支组合梁的承载能力和适用跨度.发展新型弦支钢-混凝土组合梁，不仅继承张弦梁体系受力性能高效的优点，还进一步发挥钢-混凝土组合结构的组合作用优势，取得施工便捷、承载能力和跨越能力显著提高、振动舒适度改善的效果.开展新型弦支组合梁体系的研究，将其推广应用于超大跨楼盖结构中，具有良好的发展前景.

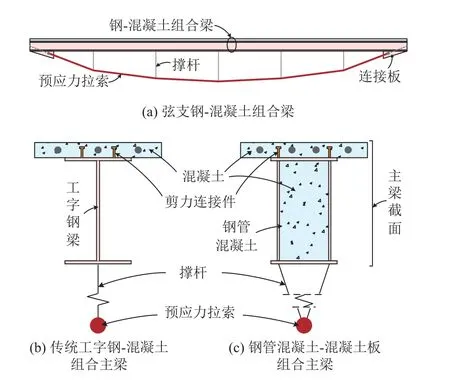
图11 弦支钢-混凝土组合梁及其截面形式示意图Fig.11 Schematic illustration of cable-supported steel-concrete composite beam and its cross-section

4 结论

针对现有组合楼盖优化设计研究中缺乏对超大跨组合楼盖的分析、优化变量和约束设置不充分等不足，借助广义简约梯度算法研究大跨度钢-混凝土组合楼盖的优化设计问题.以组合楼盖的经济等效用钢量最小值为目标，对于跨度在10～100 m，承受可变荷载2～10 kN/m2的单向组合楼盖截面进行优化与分析，主要结论如下.

1）钢-混凝土组合楼盖的最优钢梁梁高由总梁高限值确定，截面采用上翼缘较小的单轴对称焊接工字钢，以充分发挥下翼缘的抗弯承载效率.当组合楼盖跨度小于60～70 m、荷载小于6 kN/m2的工况下，经济适用性强.对于超大跨的楼盖结构，传统工字钢-混凝土组合楼盖设计的抗弯承载效率降低、用钢量增加迅速.

2）楼盖组合梁优化截面的腹板抗弯承载效率相对翼缘较低，若在超大跨度需求时继续采用传统工字钢-混凝土组合楼盖设计，腹板面积占钢梁截面的比例迅速增大，由此导致组合楼盖的经济性下降.楼盖组合梁优化截面的塑性中和轴位置随跨度和所受荷载的增大而下移.从跨度60 m开始，塑性中和轴位置靠近腹板中部，楼盖的组合梁受力特点接近纯钢梁，此时组合楼盖的组合作用已经不能充分发挥，从而导致经济性减弱.

3）结合参数分析的结论，从组合梁截面特性和受力机理的角度探讨超大跨度下组合梁截面的发展趋势，通过降低腹板区域的用钢比例达到减小用钢量、提高承载效率的目的.以此为基础，展望了波形钢腹板组合楼盖和新型弦支组合楼盖的发展.新型弦支组合楼盖继承张弦梁体系受力性能高效的优点，还进一步发挥钢-混凝土组合梁的组合作用优势，可以有效提高楼盖的承载能力和经济跨度.