基于损伤区域融合变换的轴承鼓形滚子表面损伤检测方法

艾青林，崔景瑞，吕冰海，童桐

(浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室，浙江 杭州 310023)

滚动轴承在工业中有着广泛的应用，是极为重要的传动部件，其动态性能对机械系统有重要影响[1].滚子作为轴承中最为重要的零件，其表面质量决定了轴承的使用寿命及运动性能，而滚子表面损伤不同的成因给损伤检测带来一定困难.传统的轴承滚子表面损伤检测方法有涡流检测[2-3]、超声波检测[4-6]、磁粉检测[7]等，这些方法存在系统稳定性较差、环境适应能力不足等问题.

近年来，机器视觉逐渐被应用于零件表面缺陷检测中.陈昊等[8]建立光流误差估计模型分割出轴承滚子表面缺陷区域；Chan等[9]基于表面损伤的形变利用反射条纹图案技术检测损伤；段志达[10]综合伽马矫正算法、模板匹配与霍夫变换等机器视觉方法设计了轴承缺陷检测系统；尚鲁强[11]使用机械臂采集工件图像，并用图像平滑与图像锐化算法识别曲面缺陷；苏骏宏等[12]设计专用光学系统检测轴承表面微米级缺陷.深度学习方法结合机器视觉能同时具有神经网络强大的学习能力与图像的直观性.文生平等[13]提出一种在线计算机视觉系统结合RetinaNet网络诊断轴承滚子表面的各种缺陷；Prappacher等[14]利用模拟缺陷实现了轴承滚动体缺陷的自动检测；Xu等[15]提出一种小型数据驱动网络并结合半监督数据增强用于滚子表面缺陷检测与分类；Le等[16]与Hu等[17]分别使用Wasserstein对抗生成网络与空间通道注意力机制，缓解表面损伤数据集样本不平衡以及不足的问题.

使用神经网络检测表面缺陷需要充足并且类别均衡的训练样本，而目前鼓形滚子的生产过程高度优化，带缺陷的样本数量相对较少，这导致负样本数量有限而出现正负样本不均衡的情况，以上问题往往导致网络泛化能力较差.以滚子的主要工作面侧面为研究对象，提出一种基于多样本关键损伤融合数据增强的损伤检测方法，其中数据增强方法丰富了损伤特征从而改善了样本不均衡带来的问题，并使模型对新损伤样本具有更强的适应能力.具体步骤如下：首先根据样本中滚子外圆角分布特点对侧面图片进行预处理，对核心检测区域进行裁剪；然后基于聚类预选框及损伤评估函数从负样本数据集的损伤标注区域中选出纵横比与大小合适的关键损伤区域，对所选区域进行不同的仿射变换，并与正样本进行融合生成新的负样本，将增强后数据集输入到检测网络中进行分类并与传统检测方法进行对比，实验表明采用改进数据增强的鼓形滚子表面损伤检测模型优于传统方法，调整正样本阈值后能取得较高的查准率，满足实际生产需求.

1 滚子表面损伤检测装置

1.1 滚子图像样本采集

在对鼓形滚子表面损伤检测研究中发现，鼓形滚子零件为近似圆柱体并且工作侧面损伤分布具有随机性，这导致传统的拍摄手段不易获得样本工作侧面完整的损伤特征.多次拍摄采样会极大地影响采样效率，且目前没有公开的轴承鼓形滚子数据集，针对以上问题研制了鼓形滚子表面损伤特征样本检测装置，如图1所示.它主要由工件输送带、旋转底盘、轴承滚子及滚子各个面的拍摄相机组成.研究对象为滚子的工作面侧面，故仅采集侧面图像样本.当滚子经输送带输送时，通过底盘旋转到侧面摄像头拍摄工位拍摄侧面图像，底盘由电机控制，按照一定的时间间隔进行旋转，将拍摄完的滚子带离拍摄工位.侧面摄像头为360°外窥光学镜头，能捕获滚子端面以及呈环形的360°侧面图像，每个零件拍摄过程中保证光照条件一致.

图1 滚子面损伤图像样本采集装置Fig.1 Collection device for roller surface defect image sample

1.2 样本表面损伤分析

检测的轴承滚子为同一型号规格的鼓形滚子零件，实验数据主要由侧面摄像头获取，根据无损伤滚子分为正样本和根据带损伤滚子分为负样本.图2为滚子实物与采样获得的侧面样本各部分之间的对应关系，从图中可知，滚子工作侧面为上、下侧外圆角轮廓包围的区域.

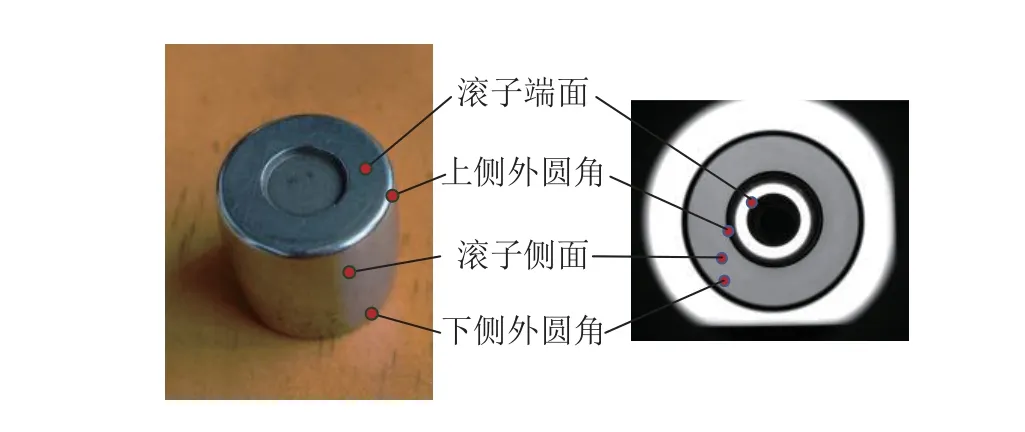
图2 轴承滚子实物与样本对照图Fig.2 Bearing roller physical sample comparison chart

采样得到的滚子侧面负样本损伤主要分为划伤、片伤、切伤、腐蚀、烧伤、凹陷、车削痕、凸点以及靠近端面的磨损等，主要损伤类型如图3所示.

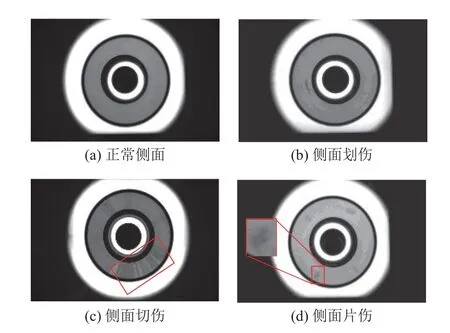
图3 滚子侧面样本不同损伤Fig.3 Different defects of roller side samples

2 基于多样本关键损伤区域融合的数据增强方法

为了增加模型对新损伤样本的适应能力，考虑将不同负样本滚子图像之间的损伤进行融合[18]以丰富损伤特征的样式，提出多样本关键损伤区域变换融合的数据增强方法.

2.1 目标裁剪处理流程

从滚子侧面损伤情况可知，负样本损伤尺度小，导致损伤不明显，并且样本侧面以外区域存在的一些无关像素而影响检测精度，针对此问题设计目标裁剪流程进行图像预处理.首先找到合适的裁剪边界并在原图中裁出对应区域以缩小目标区域(region of interest，ROI)；滚子下侧外圆角边界恰好包围损伤所在的滚子侧面区域，所以将下侧外圆角最小外接正方形作为裁剪目标，经过处理的图像具有更高的损伤特征集中度.图4(a)展现了原始滚子图像中工作侧面的目标裁剪效果.之后对正样本进行上侧外圆角轮廓提取，提取到的轮廓为后续数据增强提供边界条件.目标裁剪的难点在于如何准确提取所有样本图像轮廓特征，在轮廓提取阶段需要排除损伤区域带来的干扰.使用梯度提取、高斯滤波、二值化、形态学和边缘检测实现对全部样本边界轮廓的准确提取，以下流程以负样本为例展示轮廓提取过程.

图4 原图核心检测区域与高斯滤波后图像Fig.4 Original image’s core detection area and image after Gaussian filtering

2.1.1 原图梯度提取与高斯滤波 图像梯度提取能强调边缘特征信息，是目标裁剪的必要流程.图像中某坐标的梯度为

式中：gx与gy分别为x和y方向的梯度，梯度的幅度为

在实际过程中，以绝对值来代替平方与开方，得到梯度近似值为

使用sobel算子[19]计算图像梯度，经梯度提取后滚子图像边缘以及轮廓处有较大的像素值，在二值化时更容易归为白色像素而便于轮廓提取.由于外轮廓周围背景板的划痕、光线折射造成的光晕对图像的影响，原图在梯度提取后存在一定的噪声，故对图像采用高斯滤波[20]进行降噪，对于一个边长为2k+1的高斯核，高斯核中坐标为(i,j)的元素值Hi,j满足以下关系：

式中：σ为高斯分布的标准差.对于滚子图像来说，更大的高斯核可以更加有效地减少图像的噪声，但是也会带来计算量的增加，实验选取高斯核为9×9，σ =1.7.图4中实线框内为损伤区域，经梯度提取与滤波后的图像如图4(b)所示.

2.1.2 形态学获取下侧外圆角轮廓特征 为提取下侧外圆角轮廓，首先需要对图像进行二值化，二值化后得到结果如图5(a)所示，可以看出二值化图像轮廓部分更为清晰，外围环带状光晕得以去除.在二值化后采用形态学方法去除图像中损伤部位形成的斑点与外围残余噪声.形态学方法[21]包括腐蚀与膨胀处理，图像经过若干次腐蚀处理后，外围噪声得到彻底去除，内部白色斑点及细小圆形轮廓也被黑色像素覆盖，从实线框中可以看出损伤经处理后只有少数残留，有利于下侧外圆角轮廓检测.腐蚀后膨胀处理消除腐蚀导致的轮廓轻微不连续现象，使得下侧外圆角轮廓更加完整清晰，最终提取到的轮廓特征如图5(b)所示.

图5 经二值化后图像与轮廓特征Fig.5 Binarized image and contour feature

2.1.3 外圆角轮廓检测 对经形态学处理后的图像使用Suzuki轮廓跟踪算法[22]提取所有轮廓.为了排除残留损伤形成轮廓的干扰，根据滚子零件尺寸信息只保留所需下侧外圆角轮廓，最终目标裁剪的边界为提取到的下侧外圆角轮廓最小外接正方形.在目标裁剪后的区域排除了无关像素的干扰，并且长宽仅约900×900像素，相比于原图的1920×1200像素尺度大幅缩减，这不仅有利于网络对于输入尺度的要求，更能在图像放缩时让损伤像素不过于微小.

正样本上侧外圆角轮廓提取为后续数据增强提供边界依据.在图5(a)基础上采用霍夫圆检测法获取上侧外圆角轮廓，在得到的圆形簇中选择半径最大的圆作为上侧外圆角轮廓，结果如图6(a)所示.最终在输入网络前对图像作添加黑色边界处理以进一步覆盖无用的像素，结果如图6(b)所示.

图6 上侧外圆角轮廓与添加黑边图像Fig.6 Upper side external fillet profile and image with black border

2.2 负样本关键损伤区域融合变换

2.2.1 基于聚类预选框的关键损伤区域筛选 数据集负样本损伤区域标注如图7所示，图中加粗实线框内为数据标注的损伤区域.将标注点形成的最小外接矩形作为损伤区域.标注的损伤区域形态各不相同，为了选出合适尺寸的损伤区域为后续变换创造条件，根据k-means++聚类算法设置3种长宽比的预选框，该算法在k-means算法基础上改进了聚类中心的初始化过程.将预选框与数据标注损伤区域几何中心重叠，根据损伤估值函数计算每个损伤区域与预选框的相似度以选出关键损伤区域，使得拼贴后前景与背景有较好的几何尺寸契合度.

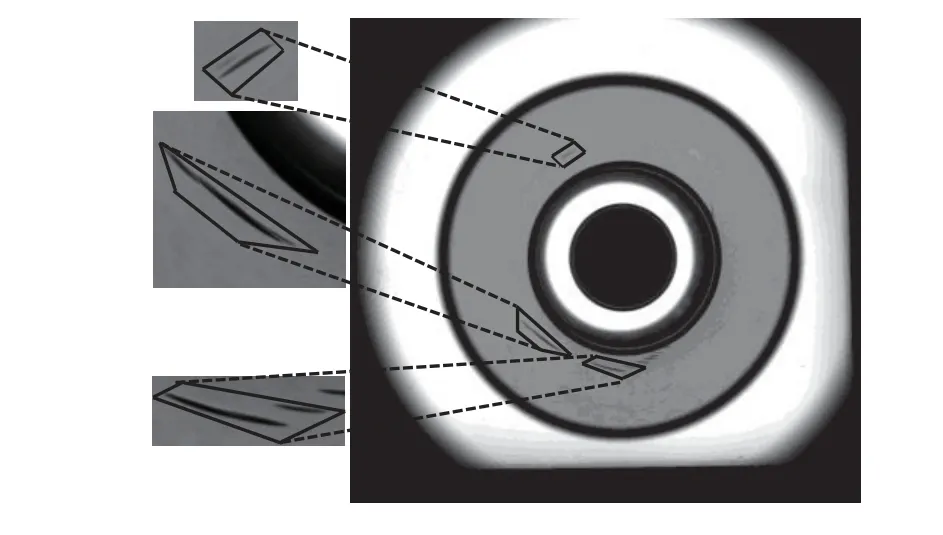
图7 损伤区域数据标注示例Fig.7 Example of defective area data labeling

根据标注损伤区域长大于宽、等于宽和小于宽的3种关系聚类算法分类数k取为3.由于标注区域可能存在过大的长宽比，为了防止该情况产生的噪声对聚类算法初始中心选取造成的影响，将长宽比5以上的损伤区域对中分割.簇中心初始化过程如下：先选取一个长宽比接近1.0的损伤区域作为首个簇中心，其长宽比为 τ1，然后计算每 个 样 本 长 宽 比 与 τ1的 距 离 函 数D(x)=τx/τ1，从而获得它被选为下一个中心点的概率P(x)：

式中：τx为当前样本的长宽比，χ为损伤区域集合.选取P(x)最大的区域为下一个中心点.最终聚类得 出3个聚类中心长宽比分别为τ1、τ2和τ3.预选框边长设为其在圆周内内外侧临界情况下的长度.为确定预选框长度随位置的变化关系，将上侧外圆角和下侧外圆角形成的几何要素近似为同心圆并建立坐标系，如图8所示.设预选框长宽比为 τ ，高 为h，与 图像 的中 心距 为r，上侧外圆角半径为r1，下侧外圆角半径为r2，两圆半径均值为r3，预选框为B，损伤区域为A，圆心为O1.图8展示了长宽比为 τ，与图像中心距为r的预选框在内外边界的各个临界位置，预选框在不同位置有不同的大小.

图8 预选框内侧临界情况与外侧临界情况Fig.8 Inner critical state and outer critical state of pre-selection box

在内侧临界的情况下，θ为上侧外圆角中心和预选框临界接触点之间连线与x轴夹角；在外侧临界情况下，γ为预选框中心和上侧外圆角圆心之间连线与x轴夹角.将r分为r∈(r1,r3)和r∈[r3,r2).在内侧临界情况下，对于一个任意的r∈(r1,r3)，不超过边界的最大预选框满足几何关系：

为得到h与 θ 的 关系，h对θ求导得

同理在外侧临界情况下对于一个任意的r∈[r3,r2) ，当γ ∈时，h近似满足

对于标注出的每一处损伤区域A，A的中心即为预选框B的中心，根据式（8）～（11）确定对应圆周 方 位 预 选 框 高 度h，根 据A的 聚 类 中 心 获 得 预 选框长宽比，A与B之间的差异可以用重叠部分面积与纵横比来描述.根据预选框与损伤区域的差异设计损伤评估函选出与预选框相似的关键损伤区域，受目标检测中矩形框交并比、纵横比惩罚项的启发[23]，定义损伤评估函数为

式中：Pe为 评估 值，k为 平衡 因 子，s为 控制 纵横 比的因子.

式中：I oU 为2个矩形区域的交并比；wA、hA分 别为损伤区域的宽、高；l为聚类中心标号，l的取值为1、2、3.

每个损伤区域对应的评估值越大则越可能被选为关键损伤.损伤评估函数过滤掉原始标注的损伤区域中有过大边长或纵横比的部分，提高数据增强前后图像契合度.因此随机取3个负样本中共N个损伤区域作为一个新的负样本的损伤来源，对所有损伤区域按照式（12）进行评估函数计算并排序，选结果较大的前 [N/3]的损伤区域用于后续变换和拼贴处理.

2.2.2 损伤变换流程 损伤变换是为了进一步丰富鼓形滚子所选关键损伤区域的特征，对于一个特定的损伤区域，对它进行变换的过程可以用若干个仿射变换矩阵来描述，仿射变换矩阵为

设初始坐标向量为X=(x,y,1)，经过若干仿射变换后坐标向量为X1=(x1,y1,1)，则应当满足

式中：Tg为有序变换矩阵.

损伤变化流程包括随机错切、随机旋转与随机缩放等流程，具体步骤如下.

1）对于纵横比小于2且长边不超过85像素的损伤不做任何变换，该条件的设定是为了保留一部分原有的特征.

2）依据纵横比进行错切.不满足1）中的损伤根据其纵横比来进行不同方向的错切，对于高大于宽的损伤区域，采用x方向的错切，反之采用y方向的错切，错切角度 α=5°～25°的随机角度.x方向正负错切变换矩阵为

式中：x1、x2分别为x轴正与负的方向，

y方向正负错切变换矩阵为

式中：y1、y2分别为y轴正负方向.

3）随机旋转与缩放.每一个损伤区域旋转角 β在0～2 π ，x和y方向缩放因子为Sx,Sy为0.7～0.9的随机值，旋转缩放变换矩阵为

式中：下标r、s分别为旋转与缩放.

经上述3步处理后的损伤就可用于损伤拼贴.

2.2.3 损伤拼贴流程 将变换后的关键损伤在新图中确定位置的过程称为损伤拼贴，新图为随机采样的正样本.图9为实际滚子图像抽象，展示了损伤拼贴的过程.滚子下侧外圆角半径为r2，圆心为O2，坐标中心与O2重叠，上侧外圆角半径为r1，圆 心 为O1，损伤区域中心到原图像中心距离为r0.变换后损伤最小外接矩形为损伤区域，长宽分别为w、h.拼贴过程如下.

图9 损伤拼贴对照图Fig.9 Defect collage comparison chart

1）确定待拼贴损伤区域中心到新图中心之间距离r.r过小会导致损伤区域超出上侧外圆角边界，r过大会导致损伤区域超出背景边界.r在r0基础上添加一个满足均匀分布的随机扰动 Δr～U[-5,5] ，即r=r0+Δr，U为均匀分布.

2）随机选择旋转角.在0～2 π随机选取一个角度 γ作为旋转角，拼贴步骤中 γ为损伤中心与图像中心连线与x正半轴夹角，有了r以及 γ就可以确定损伤位置.

3）判断损伤是否超出上侧外圆角边界.损伤矩形区域离上侧外圆角最近的顶点坐标根据其位置不同而不同，如图9将全图划分为4个象限，记损伤矩形离原点最近顶点坐标为 (x3,y3)，上侧外圆角圆心的坐标为 (x4,y4)， 损伤区域点的集合为V，则两者不重合的条件为：对任意点d∈V，L(O1,d)≥r1，L(·)为点间距，上述条件排除损伤所在矩形与上侧外圆角相切的情况可以近似得：(x3-x4)2+(y3-y4)2≥r12，超出上侧外圆角边界的损伤舍弃.另外如果有损伤超出图像边界，则修剪该损伤至边界以内；如果出现拼贴的损伤恰好重叠的情况，则后者覆盖前者.原始损伤样本与经过损伤筛选、损伤变换与损伤拼贴后得到的新的负样本如图10所示，轴承滚子损伤检测总体流程如图11所示.

图10 经过损伤变换后生成的负样本Fig.10 Negative samples generated by defect transformation

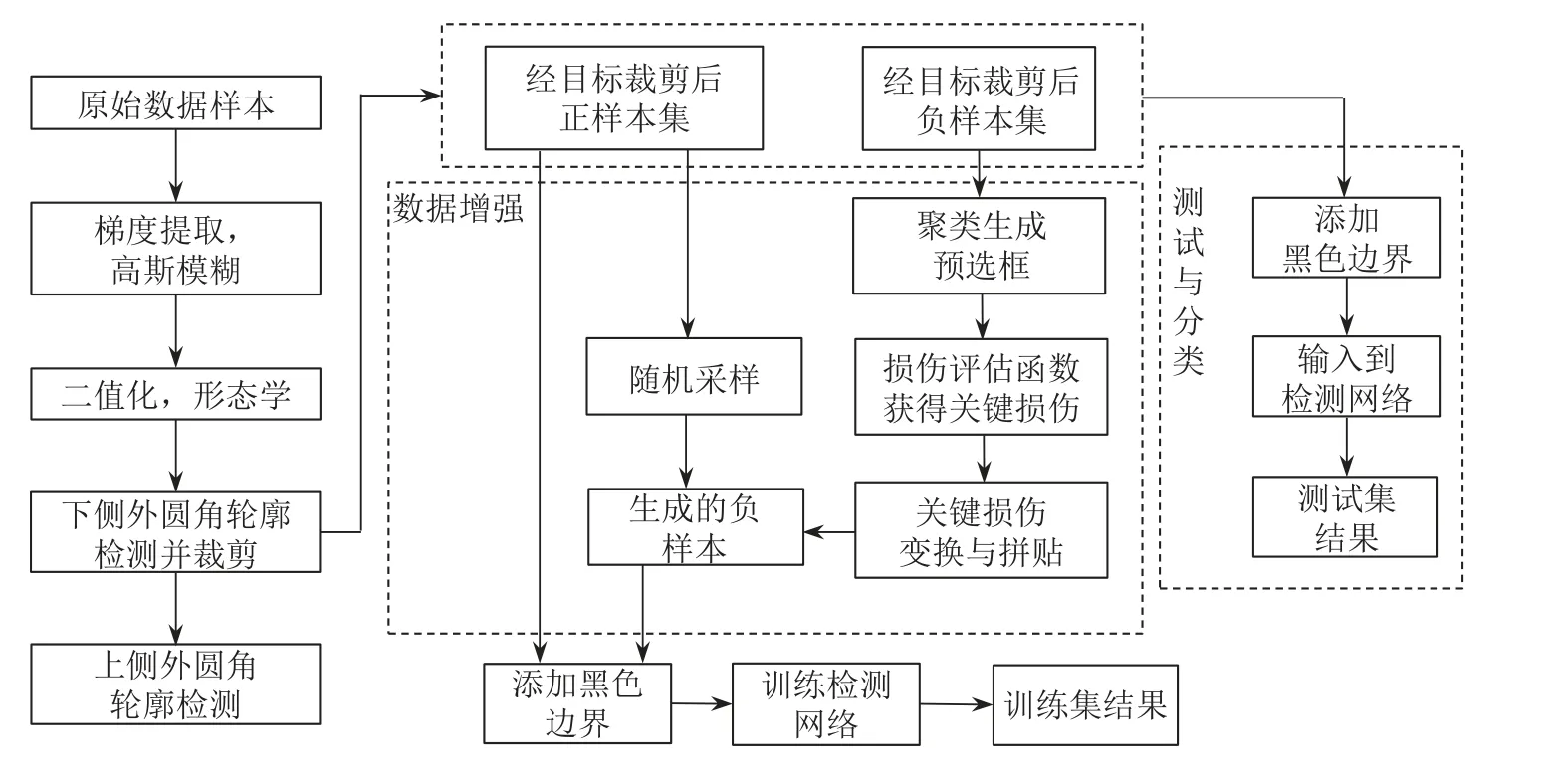
图11 轴承鼓形滚子整体检测流程图Fig.11 Flow chart of overall inspection of bearing roller

3 滚子分类网络与损失函数

3.1 检测神经网络调整

实验所进行的滚子分类任务数据集规模中等，采用小型网络无法取得理想的效果，最终所选分类网络为ResNeXt101_32×8网络[24].ResNeXt101网络最基本的结构单元设计受单个神经元的启发，单个神经元输出值为上一层每个输入向量乘以各自的权重后相加，ResNeXt101_32×8将所有输入向量对应为特征图，乘以权重的操作对应为卷积操作，相乘后的相加操作对应为聚合特征响应.在结构上，ResNeXt101采用多个Building Block块堆叠，使得每块形式简洁，保留残差结构的同时还具有分离变换聚合的思想，最终输出为

式中：x、y分别为输入、输出的特征图；c为分组卷积的组数，在ResNeXt101_32×8中，c=32，每一组卷积核通道数为8.

将输入图像长宽设定为512像素，并将网络最后的全连接输出数量改为2以对高级别语义特征进行分类操作.

3.2 改进的交叉熵损失函数

分类任务使用的函数为交叉熵损失函数，交叉熵损失函数反映的是训练所得的数据空间与样本真实空间两者分布的差异程度表达式为

式中：p为概率向量，q为one-hot向量，n为分类的类别数.

实验正样本的数量约为负样本数量的2倍，正负样本之间存在微小的样本不均衡问题，Focal Loss损失函数可以缓解这个问题[25].Focal Loss最初被用于解决目标检测中归属背景的负样本远远多于包含前景的正样本而产生的类别不均衡问题.实验是二分类问题，二分类问题中交叉熵损失函数为

式中：p1为第一类的概率，q1为真实样本标签，-lnp1为 正 样 本 产 生的 损 失，- ln1-p1为 负 样本 产生的损失.最初的Focal Loss加入平衡因子 α 控制正负样本损失并使用权重因子来控制高置信度样本损失，而本实验中仅需要对正负样本产生的损失进行平衡，故将权重因子设为1.0并改变 α，设计新损失函数为

调 整 α即 可 调 整 正 负 样 本 的 损 失 比 例，当α在0～1.0时，正样本的损失得到抑制，负样本的损失得到放大，因此模型会倾向于将正样本判为负样本，将负样本严格判为负样本，这与模型的设计初衷一致，即希望模型的查准率高，同时可以牺牲一定的查全率以及准确率.

4 实验结果与评估

4.1 数据集与实验环境

由于缺乏相关高质量公开数据集，数据集通过自制方式获得.使用现有的轴承滚子样本拍摄共获得侧面图像3174张，其中正样本（无损伤样本）2068张，负样本（带损伤样本）1106张.负样本中包含各种类型的损伤，其中片伤样本约381张，切伤样本约295张，划伤样本约319张，剩余负样本类型包含腐蚀、烧伤、凹陷、车削痕、凸点以及靠近端面的磨损.每一处损伤都使用LabelMe软件进行区域标注，在实验时从数据集中随机划分1000张作为测试集，其余2174张作为训练集.

为减小网络训练难度，首先采用迁移学习将网络参数用ImageNet数据集预训练权重进行初始化，然后采用针对性的通道归一化，即根据原始轴承滚子侧面数据集统计得到图像3个通道的均值与标准差并使用所得均值与标准差对输入图像进行标准化操作，使得输入数据分布更有利于网络的训练过程.模型在训练时采用随机梯度下降算法(stochastic gradient descent，SGD)进行梯度下降，初始学习率设置为0.001，初始动量为0.9，权重衰减系数设置为0.0005.硬件环境有：2颗Intel E5-2680V2型CPU、32 GB内存和GTX10708 GB GPU.软件环境有：Ubuntu18.04系统、Python 3.6.12、Pytorch1.7.0、OpenCV3.4.2和CudaToolKit 10.1.243.

4.2 实验指标与实验组别

在鼓形滚子的实际生产过程中，生产厂家出场的合格品应当保证一定的合格率，该合格率要由查准率来保证，一味追求查准率会导致大批的合格零件被淘汰，因此应当保证一定的准确率.本次实验采用平均准确率，查准率以及查准率与查全率的综合度量Fδ作为评价指标，平均准确率体现了模型整体的判断水平，查准率体现了产品检出合格率，Fδ是查准率(Pc)和查全 率(R)的权衡.平 均 准 确 率Pa，查 准 率Pc以 及Fδ的 公 式 为

式中：TP、TN、FP、FN分别为真正例、真反例、假正例、假反例；δ为度量查全率对查准率的相对重要性，本次实验侧重查准率，将 δ设为0.5.

为了比较不同数据增强方法的效果，将实验进行如下分组.首先是原图，即对拍摄图像不作任何处理直接进行训练.在原图上的改动有2种方法：仅使用目标裁剪(J组)和目标裁剪后旋转并填充黑色背景(K组)，从中挑出更优的一组作为基准.在基准上分别采用常用数据增强方法色彩抖动(对比度、亮度)、清晰度变换以及所提损伤筛选变换融合的数据增强方法，这些方法单独作用以判断每种方法的效果，各组测试集仅作目标裁剪与添加黑色边界处理.各组训练集应用数据增强后的图像如图12所示.

图12 不同数据增强方法处理的结果图Fig.12 Results of different data augmentation methods

4.3 实验结果与对比

4.3.1 网络损失函数参数选取 3.2节中网络损失函数参数 α会影响正负样本损失的平衡程度，通过实验来获取合适的 α，实验结果如表1所示，当α 设为0.5时，模型有较高的查准率以及Fδ.

表1 损失函数不同α值对模型指标的影响Tab.1 Influence of different alpha values of loss function on model indicators

4.3.2 不同数据增强方法单独作用对比 首先比较J、K组相比较于原图的效果，各组测试集准确率与查准率如表2所示.J、K这2组相对于原图准确率都高出10%以上，说明目标裁剪获取核心检测区域的有效性.比较J、K可以看出K组更优，这说明了旋转与外围添加黑色边界消除无关像素的有效性，后文将K组作为基准.

表2 原图与2种裁剪方法在测试集上结果对比Tab.2 Comparison of original image and results of two cropping methods on test set

为定量分析不同数据增强方法的效果，在K组的基础上进行色彩抖动、清晰度和损伤变换方法之间的对比.在进行色彩抖动与清晰度的算法设计时引入2个参数u和v.u为训练集使用数据增强方法的概率，训练集中有u比例的样本会进行该数据增强；v为控制数据增强参数调整范围，该调整范围是数据增强变换的程度，具体调整区间为 ( max(0,1-v),1+v)，通过随机在该范围内取值，达到对亮度、对比度以及清晰度强弱变换的控制.在进行损伤变换实验时，可调节的参数仅为概率u，新生成损伤样本个数为训练集正样本数量与u的乘积.实验以0.1为间隔改变u和v值.本研究选取了几组色彩抖动与清晰度的实验结果如表3所示，损伤变换实验结果如表4所示，通过分析可得出以下结论：

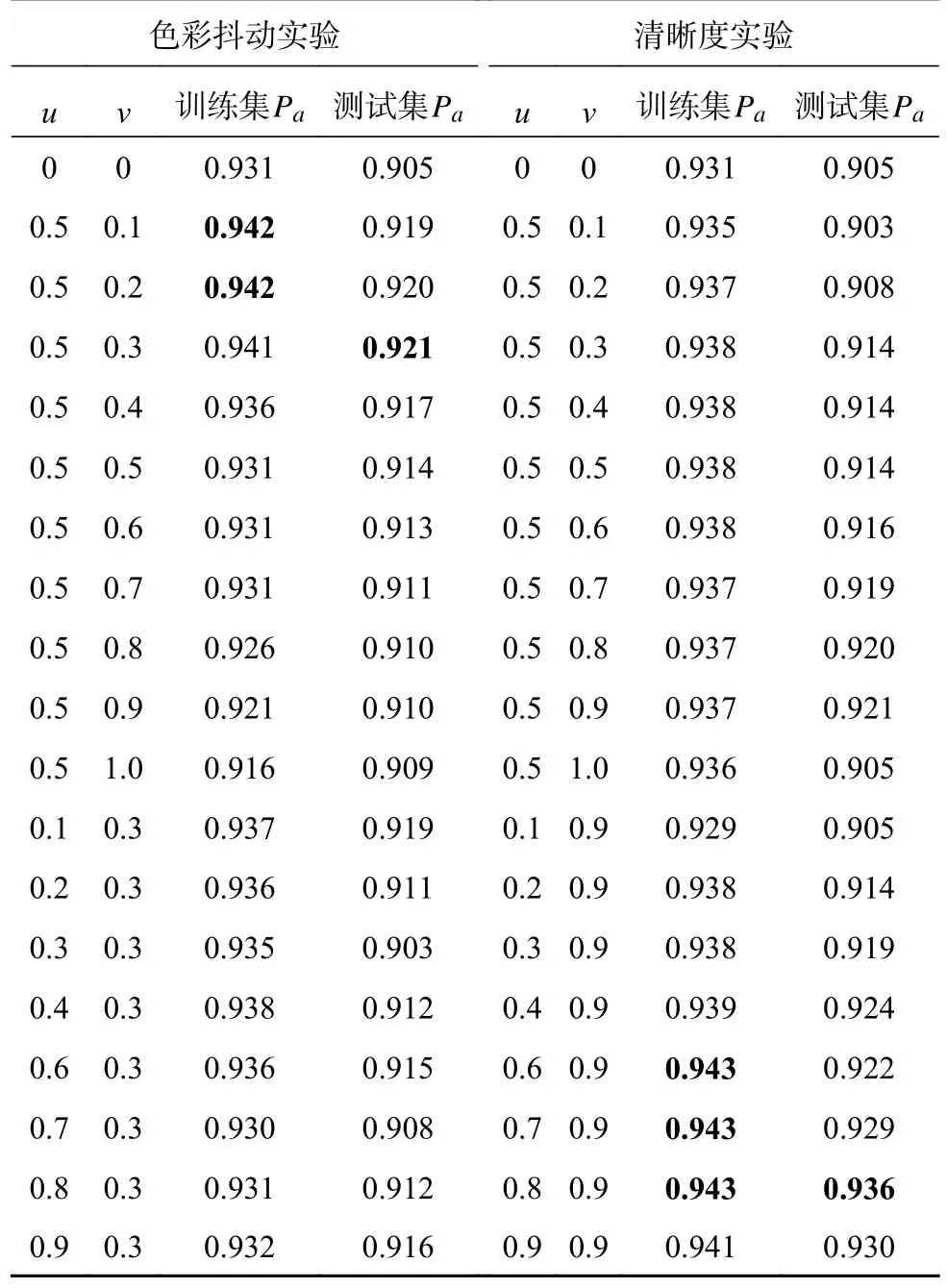
表3 滚子样本色彩抖动和清晰度实验Tab.3 Roller sample color jitter and clarity experiment

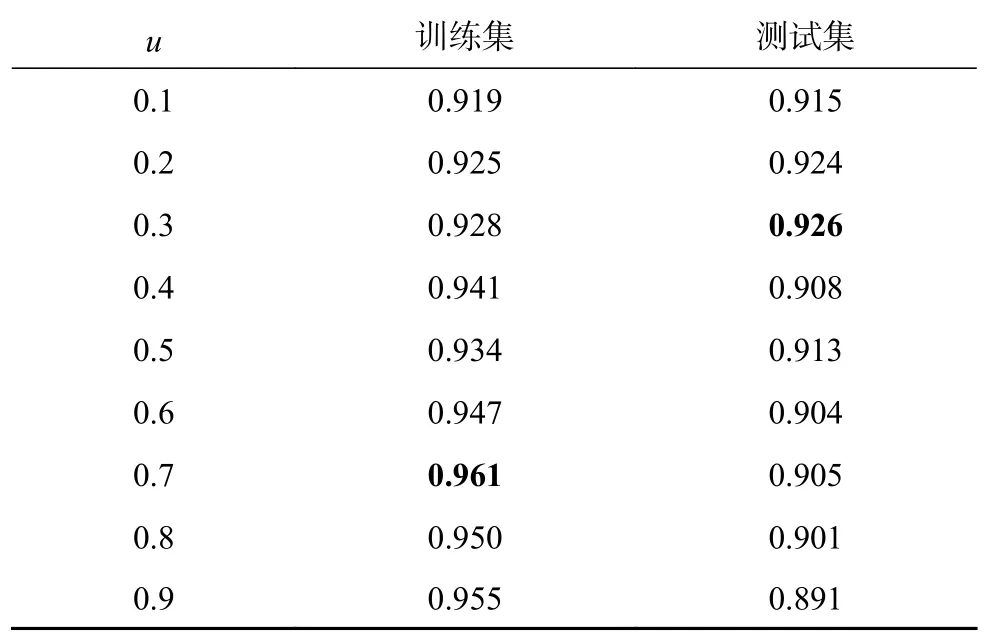
表4 滚子样本损伤变换实验Tab.4 Roller sample defect transformation experiment

1)色彩抖动与清晰度数据增强参数设置对结果影响有如下特点：当色彩抖动实验中概率u设置为0.5，v设置为0.3时，准确率最高，过大的u值会导致准确率的降低，当清晰度实验中u设置为0.8，v设置为0.9时，准确率最高.

2)对于损伤变换，当u为0.3时，验证集准确率最高，继续增大u出现过拟合现象，可推测过大的概率值会导致数据集样本分布产生偏离，从而影响测试集的准确率.

3)3种数据增强方法相对于基准测试集准确率分别提升至91.9%、93.1 %和92.6%，说明所提数据增强效果优于色彩抖动，略差于清晰度变换.

4.3.3 不同数据增强方法组合效果比较 为达到最佳分类效果，考虑同时使用3种数据增强方法.在对比实验中为了方便表示，将原图标记为组别1，基准标记为组别2，基准与色彩抖动标记为组别3，基准与清晰度变化标记为组别4，基准与损伤变换标记为组别5，基准结合色彩抖动、清晰度与损伤变换标记为组别6，每组训练50个批次，6组对应的训练集测试集平均准确率(Pa)、损失(L)和迭代次数(N)如图13所示，各组最终结果如表5所示.

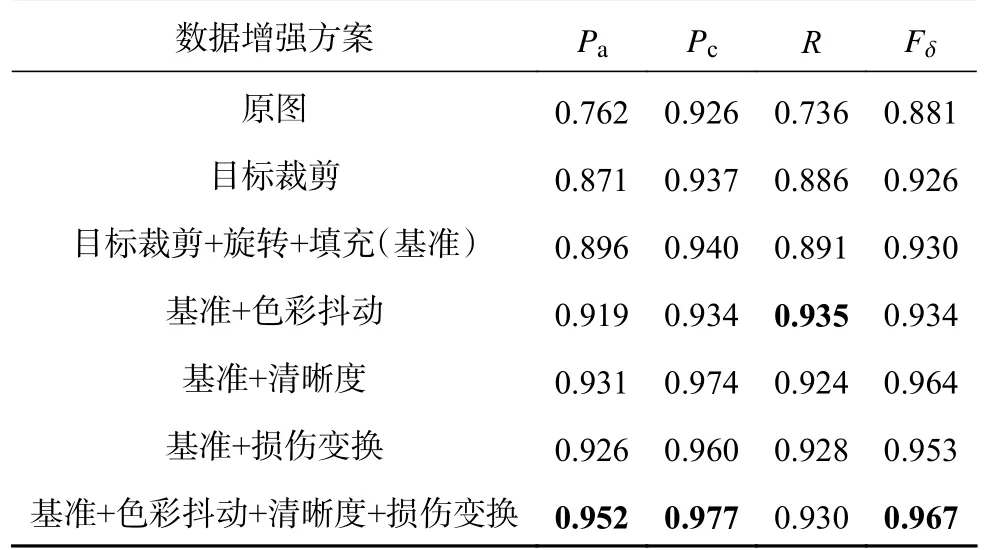
表5 不同数据增强方法名性能测试结果Tab.5 Performance test results of different data augmentation methods

图13 不同数据增强方法下的准确率与损失变化Fig.13 Accuracy and loss variation under different data augmentation methods

组1和组2都出现了过拟合现象，训练集准确率接近1且损失值接近0，而测试集损失发散，组2测试集准确率高于组1，但无法到达较高水平.通过组别2与组别3、4、5的比较可以看到色彩抖动、清晰度变换、损伤变换数据增强方法均能解决过拟合的问题，观察测试集的准确率可以发现清晰度数据增强相对于其他2种数据增强方法准确率波动较大，收敛性略差，观察表5可以看出损伤变换数据增强准确率高于色彩抖动0.7%，而低于清晰度变换0.5%.最后对比组别6与组别3、4、5可以看出，组6在第30个周期附近收敛后测试集准确率达到最高，证明了所提数据增强方法对于模型泛化性能的提升.从表5可以看出色彩抖动、清晰度变换在基准基础上准确率分别提升2.3%和3.5%，加上损伤变换后准确率又提升3.3%和2.1%，同时组别6在保证准确率的同时还能获得较高的查准率.另外，本研究对模型在线计算耗时进行实验，因为不同组别测试集处理方式相同且模型大小相同，所以各组计算耗时较为接近，实验选择组别6进行.单张图片在线检测耗时包含目标裁剪、添加黑色边界所用的图像处理时间以及图片在模型中的推理时间，这2个部分的耗时分别为190.8 ms和26.3 ms.单张图片平均处理时间为217.1 ms，满足在线检测过程的实时性需求.

4.3.4 查准率调整 在实际生产过程中对滚子产品有极高的要求，即不允许出现次品被误判成正品，所以查准率是一项非常重要的指标.在网络的输出中，可以通过提高归类为合格品的阈值来提高查准率指标，网络经过softmax函数得

式中：z为输出值，zi为第i个节点的输出值，K为输出节点的个数.设归类正样本的阈值为t，由于滚子好坏为二分类，默认阈值为0.5，提高阈值可以提高查准率.采用组别6训练模型并改变阈值t得到对应的准确率以及查准率如表6所示.随着阈值的提高，分类的准确率有所降低，但是查准率得到不断的提升，当阈值达到0.9时，查准率已经接近1，该实验证明提高分类标准可以有效地提升查准率，接近生产标准.

表6 不同样本阈值对准确率与查准率的影响Tab.6 Influence of different positive sample thresholds on accuracy and precision

5 结论

1)采集了轴承鼓形滚子侧面图像样本，对样本进行损伤融合变换数据增强并应用于滚子表面损伤检测，实验表明该方法能有较高的平均准确率与查准率，并且检测耗时满足在线检测要求.

2)实验表明采用改进数据增强的鼓形滚子表面损伤检测模型在测试集上的准确率为95.2%，查准率为97.7%，准确率与传统检测方法对比提高2%～3%，单张图片在线检测平均耗时约为0.22 s.

3)根据工厂实际生产需求，本研究的实验结果表明随着阈值的不断提升，准确率虽有所下降但是查准率不断提升，将阈值调至0.9时，查准率能达到99.8%，这样更能满足实际生产需求.

4)进一步研究为损伤融合后样本的损伤部位与背景之间的色差对检测准确率的影响，据此优化损伤融合策略实现更优的检测效果，推向产业化.