控制同步发电机加速功率的储能滑模控制器

赵影，王达，倪佳华，凌永辉，项基，郑婷婷

(1.国网内蒙古东部电力有限公司，电力科学研究院，内蒙古 呼和浩特 0100101；2.浙江大学 工程师学院，浙江 杭州310027；3.浙江大学 电气工程学院，浙江 杭州 310027)

电力行业助力实现“双碳”目标的首要任务是推动能源低碳转型、构建以新能源为主体的新型电力系统，然而新能源的波动性给同步机之间的功角稳定带来不利影响[1-2].通过实现四象限灵活调节和迅速响应，储能成为平抑新能源波动的主要手段，亦能够参与系统频率调节，增强系统稳定性[3-4].在当前大电网中，传统同步发电机仍然是主要的发电单元，因其惯量大，抗扰能力强，可预见同步发电机发电与新能源发电将长期并存[5-6].在一个含有储能与同步发电机的电力系统中，同步发电机的电磁功率与储能的有功功率在物理上具有耦合关系，即同步发电机与储能存在能量交互关系.通过利用此能量交互，储能可以通过快速地调节自身释放或吸收的有功功率，快速地调整同步发电机的电磁功率，进而调整系统扰动后同步发电机的运行动态，最终提升电力系统的功角稳定性.基于上述原理，诸多学者开展了提升电力系统功角稳定的源储互动（同步发电机-储能互动）研究.

Zhu等[7]提出一种基于仿真的储能阻尼控制器优化策略，采用粒子群算法优化储能的安装位置以及储能阻尼控制器的参数.Farraj等[8]基于参数反馈线性化，并通过设计储能的有功功率参考值，将非线性的耦合同步发电机动态转化成一个线性系统；基于此线性系统，设计一种分布式的储能控制器用以抑制同步发电机的转速振荡，以及提升电力系统的暂态(大扰动)功角稳定性.Farraj等[9]进一步分析虚假数据注入攻击对文献[8]中分布式储能控制器的影响.沿着参数反馈线性化的思路，Farraj等[10]提出一种基于实时全局信息反馈的线性反馈最优控制器，用于增强电力系统的暂态(大扰动)功角稳定性.Ayar等[11]提出一种考虑通信延时和信息物理系统干扰的分布式储能控制器.Lucia等[12]考虑传感器的测量误差，提出一种基于模型预测控制的分布式储能控制器.Farraj等[13]提出一种多智能体框架，用以应对储能的容量限制，以及传感器的测量误差和传输延迟.然而，以上文献对于储能与同步发电机的能量交互并未进行详细的建模分析，均简单地假设由储能引起的同步发电机电磁功率增量完全等于储能所吸收的有功功率.基于此假设，以上文献将原来耦合的同步发电机动态模型简化为一个线性系统，并在此线性系统上设计相应的储能控制器.

在实际电力系统中，系统运行状态受到随机干扰的影响且系统动态具有高度的非线性和不确定性.为了有效地提升电力系统的功角稳定性，基于源储互动的储能控制器应具有较高的鲁棒性能.滑模控制作为一种典型的鲁棒控制设计方法，能够较大程度地克服系统模型的不确定性，对系统干扰和未建模动态具有较强的鲁棒性.在储能控制领域中，滑模控制已有诸多研究，这些工作主要集中在储能系统设备层面的滑模控制，用于提升储能自身的动态性能[14-16].在提升电力系统功角稳定方面，Kanchanaharuthai等[17]针对含一台储能的单机无穷大系统，提出一种基于反步滑模控制的储能控制器，用于增强系统的电压调整能力和暂态（大扰动） 功角稳定性.Ni等[18]针对含一台储能、一台静止无功补偿器和一台同步发电机的电力系统，提出一种基于储能的固定时间终端滑模控制器.在上述储能滑模控制器中，储能需要获取系统范围内的电力系统运行状态，诸如无穷大母线电压、输电线路阻抗等，这些状态在实际情况下常常是难以获取的.同时，上述储能滑模控制器还需要同步发电机的转子角.在实际电力系统中，同步发电机的转子角是难以测量且耗资昂贵的[19].上述储能滑模控制器仅考虑了单机系统中单台储能参与电力系统稳定控制的情况.因此，在实际多机电力系统中，上述储能滑模控制器可能难以取得和单机系统相同的稳定控制效果.

针对上述问题，在详细建模分析储能与同步发电机的能量交互关系(即建模分析同步发电机电磁功率与储能的电气耦合关系)的基础上，提出了一种控制同步发电机加速功率的储能滑模控制器.所提储能滑模控制器通过控制同步发电机组的加速功率，使相互耦合的同步发电机解耦并实现同步发电机在系统扰动后按照期望轨迹运行，实现同步发电机功角稳定性的增强.最终通过Matlab的对比仿真算例验证了所提控制策略的有效性和优势.

1 多机系统下的电源模型

1.1 同步发电机模型

考虑具有n台同步发电机的多机电力系统，在标幺制下的同步发电机模型[20]为

式中：下标i为第i台同步发电机；δi为同步发电机转子角，单位为rad/s；ωi为同步发电机转速，单位为pu；ω0为同步发电机额定转速，单位为rad/s(一般取值为2π×50或2π×60)；Hi为同步发电机惯性常数，单位为s；Di为同步发电机阻尼系数，单位为pu；Pa,i为同步发电机加速功率，单位为pu，Pa,i=Pm,i-Pe,i，Pm,i为同步发电机机 械功率，是由原动机输入能量控制系统直接控制[20]；Pe,i为同步发电机电磁有功功率.

根据式(1)，由于一般Di较小，同步发电机的动态行为主要由加速功率Pa,i决定.在电力系统正常运行时，Pa,i=0，同步发电机处于稳定状态.在电力系统遭受扰动后，Pa,i偏离零点.此时，当Pa,i＞0(或Pa,i＜0)时，同步发电机的转速将增加(或减小).

1.2 储能模型

储能结构和本地PQ轴下的等值电路如图1所示.储能建模为一个电流源Ii=Id,i+jIq,i.其中，下 标i为第i台储能，Id,i和Iq,i分别为储能在本地PQ轴下的d轴和q轴电流.这里的本地PQ轴定义为以储能端电压为参考相量的dq轴.在dq轴下，储能的d轴电压为Vi(即储能的端电压幅值)，q轴电压为0.储能的有功功率Pi和无功功率Qi分别为

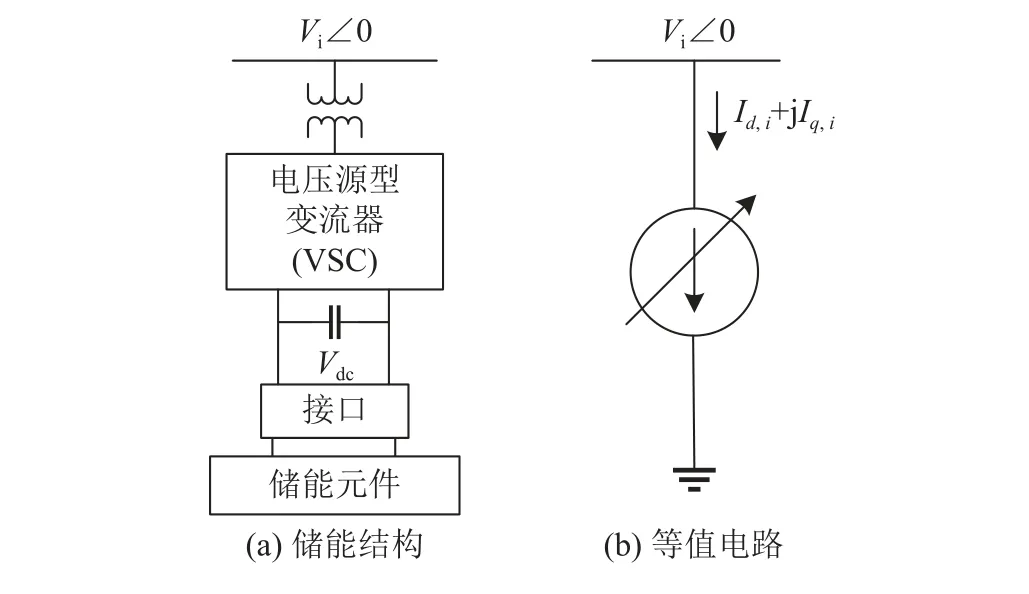
图1 储能结构与本地PQ轴下的等值电路Fig.1 Energy storage structure and equivalent circuit under local PQ axis

Pi和Qi呈解耦关系，且分别由d轴电流Id,i和q轴电流Iq,i决 定.为了 便于描述，Id,i和Iq,i为以储能端电压为参考相量的d轴和q轴电流，Id,i和Iq,i分别称为有功电流和无功电流.通过对储能中变流器的控制，有功电流Id,i和无功电流Iq,i可以快速地跟踪其参考值，闭环响应函数[21]为

2 储能与同步发电机的能量交互特性分析

2.1 同步旋转坐标轴下储能与同步发电机的能量交互特性分析

在设计储能控制器之前，首先在多机电力系统中，建模分析储能与同步发电机电磁有功功率之间的电气耦合关系，即建模分析在多机系统下，储能与同步发电机的能量交互关系.不失一般性，在建模分析过程中，考虑在每台同步发电机端口都安装一台储能，并在同步旋转坐标轴下建立多机系统模型.如图2所示，在同步旋转坐标轴下，第i台同步发电机为一个电压源和一个电抗x′d,i，其中∠δi为角 度变量.第i台储能 为一个电流源Is,i=Ids,i+jIqs,i，Yg为电力网络的节点导纳矩阵.

图2 同步旋转坐标轴下含储能的多机电力系统等值电路Fig.2 Equivalent circuit of multi machine power system with energy storage under synchronous rotating coordinate axis

根据叠加定理，第i台同步发电机的电流为

当系统未安装任何储能（图2中电流源电流均为0，仅含有同步发电机）时，有

根据式(6)：

当系统仅含有储能（图2中仅含有电流源，同步发电机暂态电势均为0）时，有

根据式(9)：

展开式(10)，则第i台同步发电机由于储能而额外增加的电流为

式中：R eal{} 为取实部，“-”为共轭运算，Poe,i为系统未安装储能时第i台同步发电机电磁功率，Pse,i为由储能引起的第i台同步发电机电磁功率增量.将式(8)代入式(13)，得：

式中：δi,k=δi-δk.

将式(11)代入式(14)，由储能引起的第i台同步发电机电磁功率增量为

式(16)表征了多机系统下储能与同步发电机电磁功率之间的电气耦合关系.第i台储能所吸收的有功功率为

Pi不等于式(16)中的这表明第i台储能所吸收的有功功率Pi并不等于第i台同步发电机的电磁功率增量.第i台储能所吸收的Pi会经电力网络影响其他同步发电机的电磁功率.更进一步，根据式(16)，第i台同步发电机的电磁功率增量还取决于自身的电气量其他储能所吸收的电流Is,k以及整个网络的导纳φi,k，特别地，网络导纳对应储能与同步发电机之间的电气距离.电气距离越小则导纳越大，储能引起同步发电机电磁功率的变化越大.若储能位置与同步发电机之间的电气距离较大，为达到同样的控制效果，储能系统需要更大的输出，对网络中其他部分的影响也加大.因此假定储能安装在同步发电机端口处，以实现对该同步发电机的控制效果最强.

2.2 本地PQ轴下含储能的多机系统建模

式中：θi为在同步旋转坐标轴下第i台储能的端电压相角.将式(18)代入式(16)，得：

在电力系统运行中，δi≈θi，因此可更进一步近似为

将式(21)代入式(12)可得第i台同步发电的电磁功率为

进而，第i台同步发电的加速功率为

最终，在第i台储能的本地PQ轴下，第i台同步发电机的模型为

3 控制同步发电机加速功率的储能滑模控制器

3.1 储能滑模控制器设计

第i台储能的控制目标是驱动第i台同步发电机的加速功率Pa,i跟踪期望值.因此，第i台 储能的滑模控制器的滑模面设计为

式中：Kω,i为大于0的比例系数.在这种设计下，当σi=0 时，即在滑模 面 上 运动[22]时，Pa,i的动态 为Pa,i=-Kω,i(ωi-1)，同步发电机按照期望的加速功率给定值运行.此时，第i台 同步发电机转速动态为

由式(27)可知，当同步发电机被强迫在滑模面上运动时，同步发电机的动态仅与自身状态量有关而不受其他同步发电机的影响，实现了强迫控制解耦.在滑模面上，第i台同步发电机的动态满足式(27)，其转速 ωi不再和电磁功率有关，而是将指数 收敛至额定值 ωi=1.0 .为实现滑模运动，σi需要在有限时间内趋近于0，即复合储能的滑模面 σi需满足[22]：

式中：ρi为比例系数.根据滑模控制的设计步骤，i一般设计为

式中：比例系数 ϵi＞0， σifi(σi)＞0 ；s gn为符号函数，它用于实现 σi在有限时间内趋近于0：

式(29)中的fi(σi) 可选取为0（对应于σi等速趋近于0）、αiσi(对应于σi指数趋近于0)或 者(对应于 σi幂次趋近于0).其中，αi＞0 ，pi和qi均为正奇数[23].选取fi(σi)为

用于实现 σi在有限时间内趋近于0.将式(31)代入式(29)，设计为

当电力系统运行于稳态时，同步发电机的加速功率Pa,i=0 、储能的电流保持不变因此式(34)中=0.当电力系统遭受扰动时，同步发电机偏离于额定值，有界且满足其中分别是的上下界且满足定义则有式(34)可写为

对于未知项，在di,eq上增加切换控制项di,sw：

其中增益 γi满足

整合式(37)和(38)，第i台储能的电流参考值为

注意到 σi=-Kω,i(ωi-1)-Pa,i，负荷突变、故障等系统扰动所引起的Pa,i和ωi的变化都体现在滑模面 σi的变化上.所提控制策略利用滑模控制对干扰的强鲁棒性进行匹配，利用控制滑模面趋向于0来应对不同的干扰和故障的冲击.

这种强鲁棒性成立有2个前提.1）干扰和故障带来的冲击与不确定性不能太强，需要满足的条件；2）控制律式(40)不能超过储能自身的能力.当扰动过于严重，例如发生三相短路故障时，加大，同步发电机的和 ωi同时减小.此时，所设定的滑模面σi将 急 剧 增大，控制律式(40)将快速达到电流限制，储能不再有能力使同步机运行至滑模面，滑模控制也将失 效.最后，切换控制的增益 γi在参数精确已知的情况下，将具有最小值而此参数的未知范围Δi越大、下界ηi越小，那么增益 γi也就越大，电流参考值达到极限可能性也越大.

3.2 储能滑模控制器稳定性分析

考虑如下李雅普诺夫函数为

Γ(σ)的时间导数为

根据所提的控制律式(40)可得

将(45)代入(44)可得

注意到

故

根据式(48)，Γ (σ)将 在有限时间内收敛至0.在所提储能滑模控制器下，每台储能的滑模面 σi将在有限时间内收敛至0，即 σi→0,∀i=( 1,2,···,n).在所提储能滑模控制器下，每台同步发电机的加速功率Pa,i将在有限时间内跟踪上期望值-Kω,i(ωi-1)，即同步发电机按照期望的轨迹运行.更进一步，同步发电机的转速动态变为式(27)，实现同步发电机动态之间的解耦.

3.3 实用化储能滑模控制器

为了削弱滑模控制中的抖振现象，采用如下非线性的光滑函数去近似式(40)中的符号函数[22]：

式中：比例系数 μi＞0.最终，整合式(49)和式(40)， 第i台储能的电流控制为

式中：Kω,i＞0, σi=-Kω,i(ωi-1)-Pa,i, αi＞0, ϵi＞0,μi＞0.

当采用式(49)近似符号函数时，稳定性分析中的式(47)变为

根据式(41)可以看出，采用式(49)替代符号函数可以得到

可以看出系统是指数收敛的.虽然不同于式(48)得到的有限时间收敛，但是同样能够保证系统的稳定.

图3直观地展示所提控制同步发电机加速功率的储能滑模控制器.如图3(a)所示，储能仅需要测量本地同步发电机的加速功率Pa,i和ωi-1，并根据图3(b)中的滑模控制规律计算出储能的有功/无功电流参考值.在整个储能控制中，储能仅需要本地同步发电机的运行状态(即Pa,i和ωi-1) ，并且不需要难以测量的同步发电机转子角[19].类似于电力系统稳定器[24]，图3(b)中的滤波环节是用于过滤Pa,i和ωi-1在正常运行状况下的慢速变化.Tω,i的值并不严格，可以取值在1～20 s[24].图3(b)中的限幅环节是为了防止储能的过流运行.

图3 实用化储能滑模控制器Fig.3 Practical sliding mode controller for energy storage

4 仿真分析

通过仿真实验验证提出的控制同步发电机加速功率的储能滑模控制器.在仿真中，所有的测试均在Matlab/SimPowerSystem上实现，仿真模式均选择为相量模式.所有仿真均采用系统的非线性模型，负荷均采用恒阻抗模型.

4.1 算例1 四机两区域系统

如图4所示，本小节采用四机两区域系统进行仿真分析.系统仿真模型与运行数据(包括同步发电机、调速器、自动电压调节器、励磁系统、负荷、电力网络参数以及潮流数据等)下载自文献[25].在所有仿真测试中，系统初始运行于稳态.

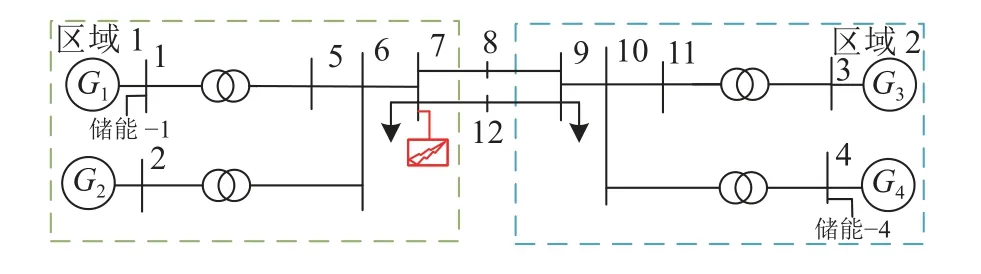
图4 四机两区域系统结构图Fig.4 System structure diagram of four generators and two areas

在仿真中，G1和G4端口安装一台储能（图4中储能-1和储能-4）.2台储能的标幺系统均采用与最邻近同步发电机相同的基准值，即均为最邻近同步发电机的额定值.G1和G4的额定值相同，G1和G4的初始发电功率均为Pm1=Pm4=0.78pu，系统的总发电功率为=3.13pu（以储能-1（或储能-4）基准值标幺化）.储能-1和储能-4的容量均为0.10 pu，即G1（或G4）额定值的10%.根据参考文献[21]，储能的电流响应时间一般为0.5～5.0 ms.为了更保守地考虑响应时间对控制的影响，选取时间常数的最大值5.0 ms进行仿真分析，确保在其他的时间常数情况下，能够保证仿真的稳定和较好的控制效果.因此，储能的电流响应时间均为 τi=5.0ms.

选取3种不需要通信、也不需要同步发电机转子角反馈的储能控制器进行对比实验.它们分别为：Farraj等[8]提出的参数反馈线性化(parametric feedback linearization，PFL)控制器、Zhu等[7]提出的功率振荡阻尼(power oscillation damping，POD)控制器以及Ling等[26]提出的柔性控制器(flexible controller，FC).PFL的控制规律为：的控制规律为：FC的控制规律为：其中Po,i为第i台储能与第i台同步发电机的总 输出有功功率.PFL、POD与FC中为第i台 储 能所吸收的有功功率参考值.FC的参数直接来源于文献[26]，即.所提控制器的Kω,i与相同，即=8，其余参数设置为αi=10.00 、ϵi=0.10 、γi=1.50 、μi=0.15 以及Tω,i=1.00 s.在对比试验中，PFL与POD的反馈系数与所提控制器的Kω,i相同，即Kω,i=8.

在同步发电机电压调整实验对比中，仿真结果如图5所示，其中横坐标为时间t，纵坐标分别为相对转子角偏差δ1-δ4和同步发 电 机端电压Vt1.在t=1.0 s时，G1的端电压参考值Vt1,ref提高5%(如图5(b)中*型线所示）.当G1 开始执行电压调整指令时，其频率 ω1开始下降，这导致同步发电机的相对转子角偏差 δ1-δ4开始减小(如图5(a)所示).对于所提控制器，δ1-δ4在大约t=3.5 s时，趋于稳定.然而，对于未安装储能、PFL、POD和FC，δ1-δ4在t=3.5 s时，仍存在较大幅度振荡.以上结果验证了所提控制器的有效性，所提控制器能更快地稳定同步发电机.此外，以上结果也表明，所提控制器能够兼容已有同步发电机控制器，即调速器、电压调节器和电力系统稳定器.

图5 G 1 端电压参考值增加5%的仿真结果图Fig.5 Simulation results when G1 voltage reference is increased by 5%

在进行短路故障实验对比中，仿真结果如图6所示，纵坐标分别为同步发电机转速 ω1和相对转子角偏差 δ1-δ4.在t=1.0 s时，在母线-7上施加三相短路故障(如图4所示)，并在3周波后清除故障.如图6(a)所示，当三相短路故障发生时，母线-7的负荷丢失，G1的转速开始增加.这导致相对转子角偏差 δ1-δ4增加（如图6(b)所示）.当母线-7的故障清除时，系统在不同情况下呈现出不同的振荡.由图可见，相比于未安装储能、PFL、POD和FC，所提控制器具有更短的稳定时间.

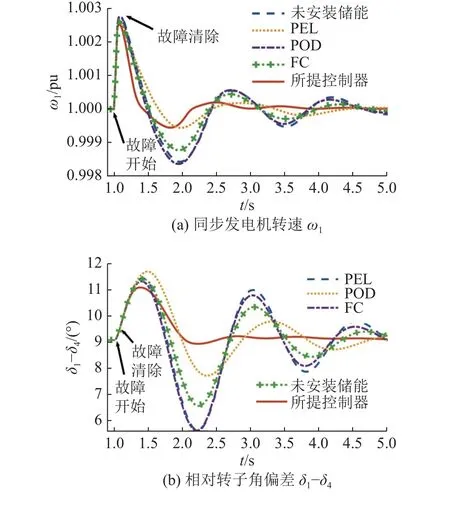
图6 母线-7短路故障的仿真结果Fig.6 Simulation results when bus 7 occurs fault

表1进一步对比 δ1-δ4的超调量.由表可见，所提储能滑模控制器相较于未安装储能减小了0.35°(未安装储能的14.77%)；相较于PFL减小了0.60°(PFL的22.90%)；相较于POD减小了0.23°（POD的10.22%）；相较于FC减小了0.31°(FC的13.30%).

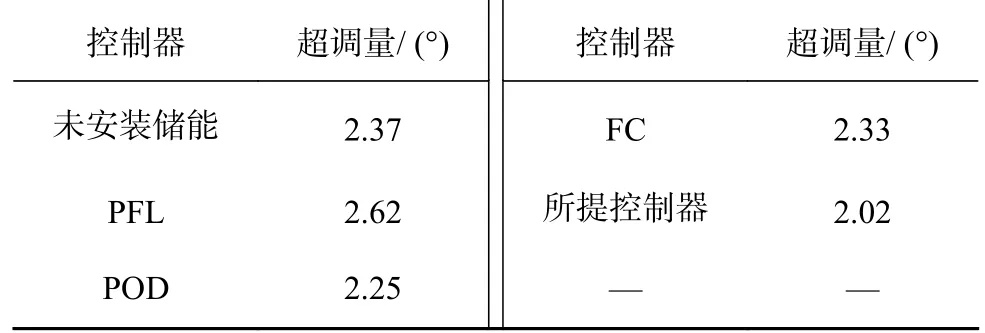
表1 三相短路故障超调量对比Tab.1 Overshoot comparison of three-phase short circuit fault

4.2 算例214机59节点系统

在如图7所示14机59节点的复杂系统中，进行所提控制策略的仿真分析，系统仿真模型与运行数据(包括同步发电机、调速器、自动电压调节器、励磁系统、负荷、电力网络参数以及潮流数据等)下载自文献[27].

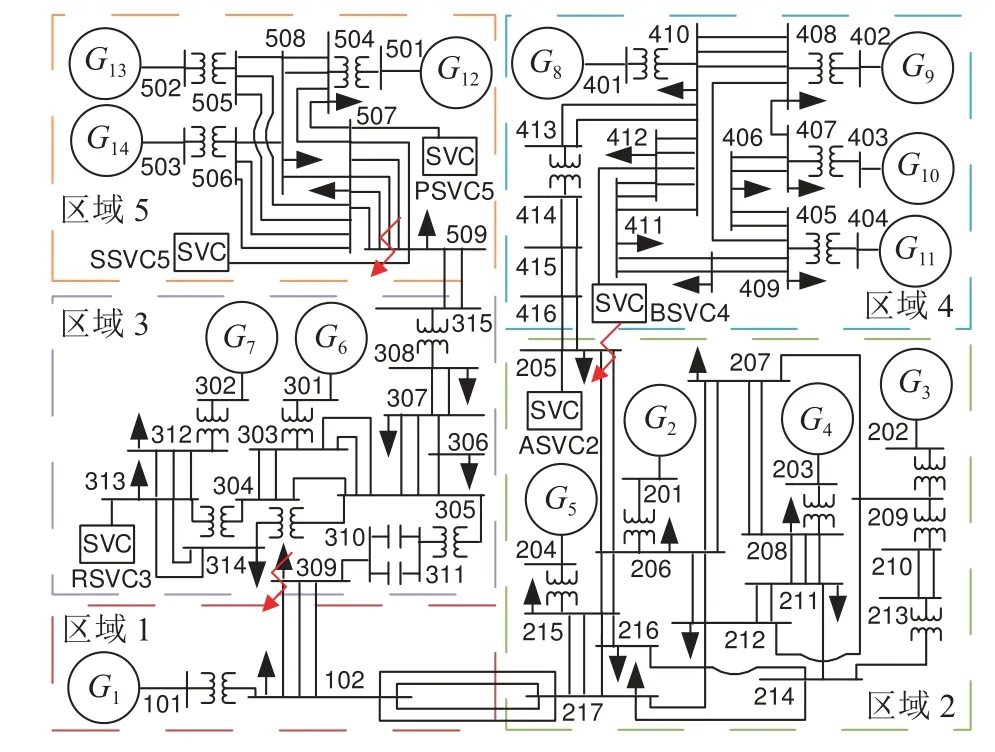
图7 14机59节点系统结构图Fig.7 System diagram of 14 generators and 59 buses

在仿真中，G1、G2、G6、G7、G8、G12端 口安装1台储能.储能的标幺系统均采用与最邻近同步发电机相同的基准值，即均为最邻近同步发电机的额定值.储能的容量均设置为0.10 pu，即最邻近同步发电机额定值的10%.储能的容量相对于系统总发电功率、系统同步发电机总容量以及最邻近同步发电机发电功率的比值如表2所示.定义同步发电机Gi端口的储能容量为，同步发电机Gi的容量为，同 步发电机Gi的发电功率为Pm,i，系统总发电功率为系统同步发电机总容量为.储能的电流响应时间均为τi=5.0 ms.

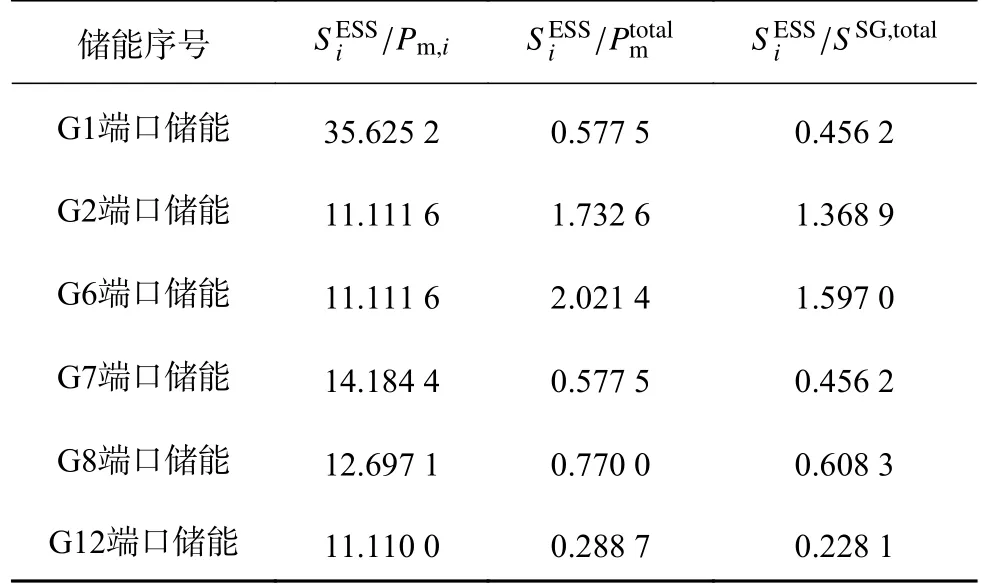
表2 不同储能容量比值Tab.2 Ratio of different energy storage capacity %

选取如表3所示的4个案例测试所提控制同步发电机加速功率的储能滑模控制器.所提控制器、PFL、POD以及FC的参数均与4.1小节相同并进行电压调整实验对比，如表3所示.将Gi的端电压参考值提高5%，对应的仿真结果如图8所示，其中横坐标为时间t，纵坐标分别为相对转子角偏差 δ1-δ14和同步发电机端电压Vt1.当Gi开始增加端电压时，相对转子角 δ1-δ14开始减小.随着时间的推移，如图8(a)所示，相比于PFL、POD和FC，所提控制器可以使同步发电机更快速地稳定.相似的情况可从图8(b)中看到.相较于PFL、POD和FC，所提控制器的Vt1能够更快速地稳定.

图8 案例1电压调整仿真结果Fig.8 Voltage regulation simulation results of case study 1

表3 14机59节点系统测试案例说明Tab.3 Test case description of 14 generators and 59 buses

对短路故障实验进行对比，如表3所示，选取3个故障来激发系统的区间振荡.3个故障的位置见图7，对应的仿真结果见图9，纵坐标分别为G2、G6和G12的转速ω2、ω6和ω12.在这些案例下，相比于PFL、POD和FC，所提控制器可以更快速地稳定受扰动的同步发电机.以上结果验证了所提控制器的有效性，也进一步展示了所提控制器的优势.

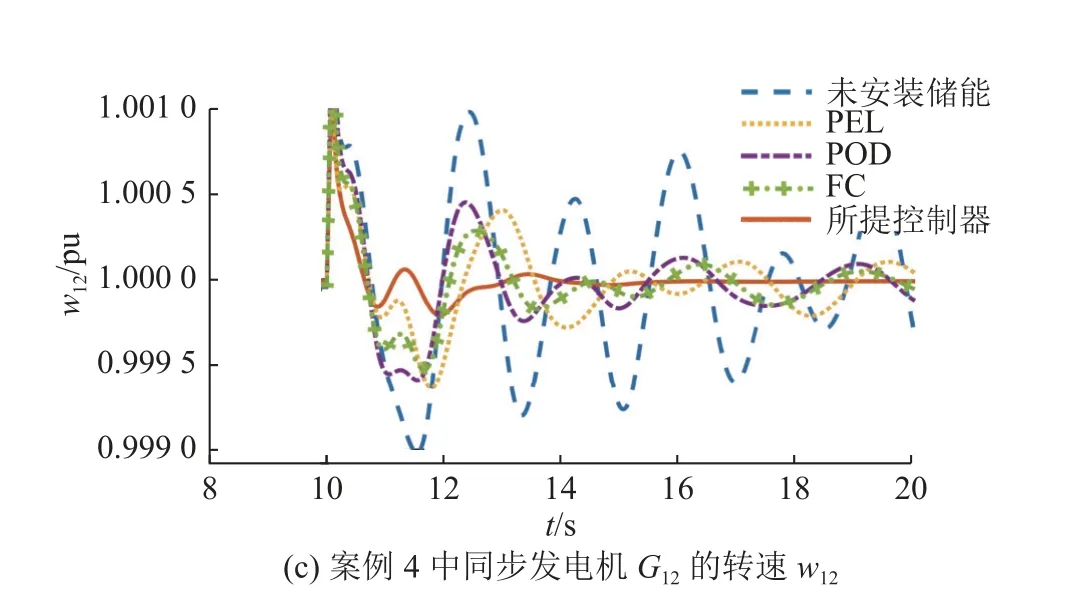
图9 案例2-4短路故障仿真结果Fig.9 Short circuit fault simulation results of case study 2 to 4

5 结语

针对新能源占比增加导致电力系统功角稳定性恶化的问题，基于利用滑模控制解耦同步发电机的思路，提出一种控制同步发电机加速功率的储能滑模控制器.在该控制器中，本地储能获取本地同步发电机的加速功率与转速信息，并通过储能的滑模控制调节储能吸收或释放的电流，进而控制本地同步发电机加速功率至期望值.该期望值为本地同步发电机的额定转速偏差比例反馈，用于实现多机系统中同步发电机之间的解耦，增强系统的功角稳定性.仿真实验验证了所提控制策略的优点和有效性.