古人都是高个子?
王佳一
最近我在学习《邹忌讽齐王纳谏》,文中提到:“邹忌修八尺有余。”什么是尺?我查阅资料发现,现代一尺约等于33.33 cm,那么邹忌的身长大约是2.66 m!都说关羽身高九尺,那算下来都差不多3米了!难道古代人都是身材魁梧的“巨人”吗?
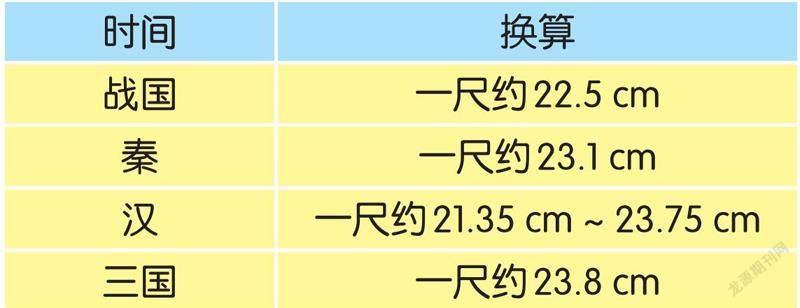
我继续查阅资料,发现尺的长度在各个朝代是不一样的。
古代的“尺”要短于今天的“尺”。邹忌是战国时的齐国人,按一尺为22.5 cm算,他的身高为22.5×8=180(cm)。而三国时期的关羽身高按一尺为23.8 cm算,也就是23.8×9=214.2(cm)。关羽虽然已经很高了,但还是没有姚明高!
最近我还学习了比例尺的相关知识,一个问题浮现在了我的脑海中:比例尺是不是像“尺”一样的长度单位呢?通过定义“比例尺是表示图上距离与实际距离之比”,我了解到比例尺=图上距离∶实际距离。得到这样一个公式,我赶紧找出一张中国地图,开始不厌其烦地去“验证”。
我测量了西安到成都的图上距离,又用图中的比例尺计算出了西安到成都的实际距离,结果和资料中的数据相差无几。经过这一波“实战经验”的积累,我更加坚定地认为:“比例尺”和长度单位“尺”是完全不一样的。
但我并没有满足于此,我发现古代还没有发明“尺”的时候,人们用一些简单的工具来度量长度。比如,可以带一根绳子在身上,需要的时候就用它来比较长短。有人想出,可以用身体的一部分作度量工具,如张开大拇指和中指,两端的距离称作1拃,一个人两臂向左右伸开的长度称为1庹。
这样说来,“比例尺”又何尝不是一把用來度量的“尺”呢?只不过比例尺度量的是图上距离与实际距离之间的比例关系。与我们常见的“尺”比起来,它是一把无形的“尺”。
我恍然大悟:原来,比例尺不是“尺”又似“尺”!一个看似简单的问题,竟也蕴含着一定的数学道理和历史知识。
710062 陕西省西安市陕西师范大学附属小学六年级(6)班
指导老师 郝高峰
本期《近似值大观园》答案:
2. 4。
4. 16个(去尾法)。
6. 4,4。
9. 进一法, 3。
12. 7个。

