高斯算法与梯形面积

胡庭玮

我最近读了一个故事，在高斯小时候，数学老师给大家出了一道计算题：1+2+3+4+5+…+96+97+98+99+100=？老师以为同学们要算很久，没想到高斯一会儿就算出了答案。他的计算方法如图1所示。

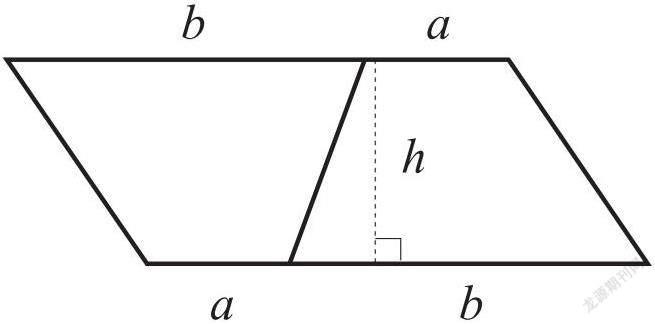
学了梯形面积公式后，我发现梯形面积公式和高斯算法有异曲同工之妙！这是为什么呢？我想应该和梯形面积公式的推导有关。两个完全一样的梯形，可以拼成一个平行四边形。平行四边形的高等于梯形的高，平行四边形的底等于梯形的上底加下底。

平行四边形面积=2S=（a+b）×h，所以梯形面积S=（a+b）×h÷2。

这种方法和高斯算法的思路差不多，只不过一种是图形，一种是数字。

我还发现高斯算法在数学上还有很多应用。

应用一：

数线段。

例：下图总共有多少条线段？

记图中每一小段距离为单位1，那么长度为1的线段共8条，长度为2的线段共7条，以此类推，长度为7的线段共2条，长度为8的线段共1条。所以，线段总数=8+7+6+5+4+3+2+1=9×8÷2=36（条）。

假设从长沙到北京的高铁，中途需要经过10个高铁站，那么需要设计多少种高铁车票，才能满足所有旅客的需求？

这其实和数线段是同一类题，不同之处在于两个站之间的票有两种：比如长沙到北京是一种，而北京到长沙是另一种，所以结果要乘以2。需要设计的总票数=（11+10+9+8+7+6+5+4+3+2+1）×2=12×11=132（种）。

数学里的知识像一张网一样，可以相互联系。难怪老师经常说：“学习数学公式，重要的是了解它的来龙去脉！”

416000    湖南省吉首市吉首大学师范学院附属小学四（7）班

指导老师    张秋银

姜露    5月7日    8：48：09

我發现当梯形的上底变成一个点的时候，梯形就变成了三角形。因为上底=0，所以三角形面积=下底×高÷2。这算不算我破解了三角形面积的秘密呢？

向阳    5月7日    10：45：23

我发现高斯算法还能运用在球队比赛的计算上呢！下周我们8个队伍进行足球比赛，每两个队分别要进行一场比赛，计算比赛的总场数就和数线段一样，总共要进行7+6+…+2+1=28（场）比赛。

王一航    5月7日    14：02：50

感谢大家的总结，现在我只用记好一个梯形公式，就能解决求和、三角形面积等问题！果然要做到“知其所以然”才能学好数学，光靠死记硬背只会十窍通九窍——一窍不通。