采用VMD和归一化峭度的钢管混凝土柱内部脱空缺陷识别方法
刘景良, 彭佳敏, 方露, 姜洋, 蔡宏爽, 张羲岭
(1. 福建农林大学 交通与土木工程学院, 福建 福州 350108;2. 福建农业职业技术学院 园艺园林学院, 福建 福州 350303;3. 福建省国电调试院有限公司, 福建 福州 350025)
服役期间的钢管混凝土结构难免遭受工作荷载和极端荷载的影响,因而会出现一定程度的脱空现象[1].脱空缺陷严重影响了钢管混凝土结构的承载力和稳定性,因此,对其进行检测和定位具有十分重要的工程意义.
目前,钢管混凝土结构脱空缺陷的检测方法包括无损检测和有损检测.常用的有损检测方法主要为钻芯取样法,即直接对可能出现脱空的位置进行钻孔取样[2].钻芯取样法虽能直观地检测出钢管混凝土试件的脱空情况,但对结构造成的破坏往往是不可逆的.常见的无损检测方法有红外热成像法、超声波法等.根据超声波在传播过程中会发生一定程度的损耗这一特性,研究人员可以探测出钢管混凝土的密度和均匀性.然而,超声波法不仅对试件本身的条件要求较高,而且需要检测人员具有丰富的检测经验,因此,其检测精度和效率相对较低[3-4].在环境温度良好的情况下,红外热成像法能够较好地识别钢管内、外表面的温度差异和内部脱空缺陷情况[5].然而,红外热成像法对气候条件要求较高,难以在阴天和背阴面的环境下进行,这极大地限制了该方法的应用范围和检测精度[6].冯琪智等[7]针对红外热成像法在缺陷处成像分辨率较低的问题,提出基于区域生长和热图信息重构的融合算法.蔡萍等[8]对压电陶瓷片采集到的波动信号进行频响函数分析,并成功检测钢管与核心混凝土之间的剥离缺陷.为克服超声波法在钢管混凝土结构缺陷检测过程中可能出现的误判现象,陈禾等[5]提出基于红外热成像法与超声波法相结合的混凝土无损检测技术.
随着新型信号处理技术的飞速发展,基于振动的损伤诊断方法在土木工程领域获得了广泛关注,其核心思想就是模态参数为物理参数的函数[9-11].虽然基于振动特性的缺陷检测方法已经广泛应用于混凝土结构缺陷检测,但其在钢管混凝土结构中的应用还并不多见.基于此,本文紧密结合钢管混凝土结构的动力特性和服役环境特点,以振动响应信号处理为出发点,采用变分模态分解(VMD)将结构响应分解为多个模态分量;然后,依据加权峭度指标选择有效的模态分量进行信号重构,并计算重构信号的Teager能量算子(TEO);最后,采用快速傅里叶变换(FFT)对TEO值进行处理和归一化峭度求解,最终达到识别钢管混凝土试件内部脱空缺陷的目的.
1 信号分解方法
为更好地从振动信号中获取缺陷信息,有必要通过信号分解方法寻找一些仅对结构损伤或缺陷敏感的分量信号,然后,根据分量信号构建损伤指标并探测钢管混凝土结构的内部缺陷.常见的模态信号分解方法包括经验模态分解[12]、集合经验模态分解[13]、补充经验模态分解[14]、解析模态分解[15],以及变分模态分解[16].其中,VMD是Dragomiretskiy等[16]提出的一种新型自适应模态信号分解方法.该方法拥有较高的运算效率,且在抗噪方面表现出鲁棒性,因而,适用于土木工程结构振动响应信号的分解.
若预设钢管混凝土结构原始振动响应信号x(t)的模态分量个数为S,则VMD可将其分解为S个模态分量,其中,第k个分量为uk(t)且中心频率为ωk(t).与经验模态分解理论不同是,经VMD分解后的模态分量信号uk(t)为1个调幅调频信号,即
uk(t)=Ak(t)cos[φk(t)].
(1)
式(1)中:Ak(t)为uk(t)的瞬时幅值;φk(t)为uk(t)的瞬时相位.
VMD本质上是通过求解模态分量的变分问题来确定各分量信号的带宽和中心频率.在各阶模态分量之和等于原信号的约束条件下,VMD将有关模态分量的变分问题转化为寻求估计带宽之和最小的模态函数.具体来说,首先,对分解后的模态分量信号uk(t)进行希尔伯特变换,得到对应的单边频谱;其次,将单边频谱与e-iωkt相乘,从而使每个分量的频谱调整至以预估中心频率ωk为中心的频带;最后,计算频率混合后信号梯度范数的平方,并估计移频后分量信号的带宽;最终,得到约束优化问题为
(2)
式(2)中:x(t),δ(t)分别为原始响应信号和脉冲函数.
为确保外界噪声情况下信号的重构精度及约束条件的严格性,首先,引入拉格朗日乘法算子λ和二次罚函数因子α;然后,采用拓展拉格朗日表达式L表征无约束优化问题,即
(3)
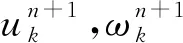
2) 设置循环条件n=n+1.
(4)
(5)
5) 迭代更新λn+1,即
(6)
6) 重复步骤2)~5),直至满足迭代收敛条件
(7)
式(7)中:ε为收敛容许值.
经过上述迭代步骤后,离散的各阶模态分量信号将从原信号x(t)中分离出来.更多关于VMD的理论和算法可参考文献[16].
2 内部脱空缺陷损伤指标
作为一种无量纲参数,峭度指标对冲击信号特别敏感,同时又富含关于损伤的信息,因而特别适合机械故障、结构损伤等方面的诊断[18].一般来说,结构损伤位置的峭度在损伤前、后会发生较大的变化,可以用来表征结构的损伤状况.除此以外,峭度还具有数学上易于处理、计算方便和有限采样时具有鲁棒性等优点.为此,将峭度指标引入土木工程领域并用于估计钢管混凝土结构的脱空缺陷位置.
在通过VMD将结构某一测点的原始响应信号x(t)分解为多个模态分量信号后,建立峭度K和相关系数C,其表达式分别为
(8)
(9)
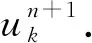
为更好地提取原始振动响应信号的有效模态分量信号,首先,构造加权峭度(KW)指标;然后,选取KW指标大于其平均值的分量为有效模态分量,并用于重构信号x′(t).加权峭度指标表达式为
KW=K·C.
(10)
在此基础上,为提取微弱损伤成分,引入Teager能量算子[19]并记作ψ.对于重构信号x′(t),其Teager能量算子为
(11)
然后,对重构信号x′(t)的瞬时TEO值进行FFT变换,即
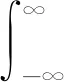
(12)
最后,针对傅里叶变换系数计算峭度指标,即
(13)
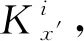
(14)
与既有的基于动力反应的损伤指标(频率、振型等)相比,采用VMD和归一化峭度识别钢管混凝土内部脱空缺陷的优点十分明显,主要表现如下.
1) VMD对噪声信号具有良好的鲁棒性,可在复杂噪声环境中提取响应信号中的关键信息.
2) 在不依赖于未损工况基准信息的条件下,文中方法也能有效识别钢管混凝土试件的内部脱空缺陷,因而具备在实际工程中的应用潜力.
3 数值算例验证
3.1 钢管混凝土柱有限元模型的建立
采用ABAQUS程序建立4根带脱空缺陷的钢管混凝土圆形柱有限元模型,如图1所示.钢管混凝土的局部冠形脱空通过布尔运算实现.钢管每根柱长1 200 mm,直径为150 mm,端板边长为240 mm,端板厚度为20 mm,钢管厚度为3.75 mm.钢材材质为Q235,弹性模量为206 GPa,密度为7.85×103kg·m-3.混凝土强度等级为C30,弹性模量为33.5 GPa,密度为2.41×103kg·m-3.

(a) 钢管混凝土圆形柱 (b) 核心混凝土缺陷
将建立的有限元模型均匀地划分为11个单元,如图2所示.在钢管混凝土圆形柱有限元模型上等间距布置11个加速度传感器,设置增量步为5×10-5s,采样频率为2 kHz,采样时间为1 s,然后,在单元1和单元2之间施加脉冲荷载,并提取不同损伤工况下每个测点的加速度时程响应.钢管混凝土柱有限元模型脱空缺陷工况,如表1所示.

图2 钢管混凝土柱有限元模型划分示意图

表1 钢管混凝土柱有限元模型脱空缺陷工况
3.2 钢管混凝土柱有限元模型内部脱空缺陷识别结果
以表1中B1工况下节点6的响应信号为例,首先,对该信号进行倒序排列;然后,再将节点信号正序排列并组成1个新的信号序列;最后,对其进行复Morlet小波连续变换,其小波量图,如图3(a)所示.图3(a)中:f为频率;t为时间.
由图3(a)可知:响应信号的频率主要集中在[0 Hz,100 Hz],[300 Hz,450 Hz],[500 Hz,600 Hz],[650 Hz,850 Hz],[900 Hz,1 100 Hz]这5个频率区间内,因此,可判断分量信号的个数为5,然后,通过VMD将目标信号分解为5个模态分量信号.在此基础上,构建节点6响应信号的各阶模态分量的加权峭度值,如图3(b)所示.
由图3(b)可知:第4阶和第5阶模态分量的加权峭度值大于平均值,可将其视为有效模态分量并进行后续操作.
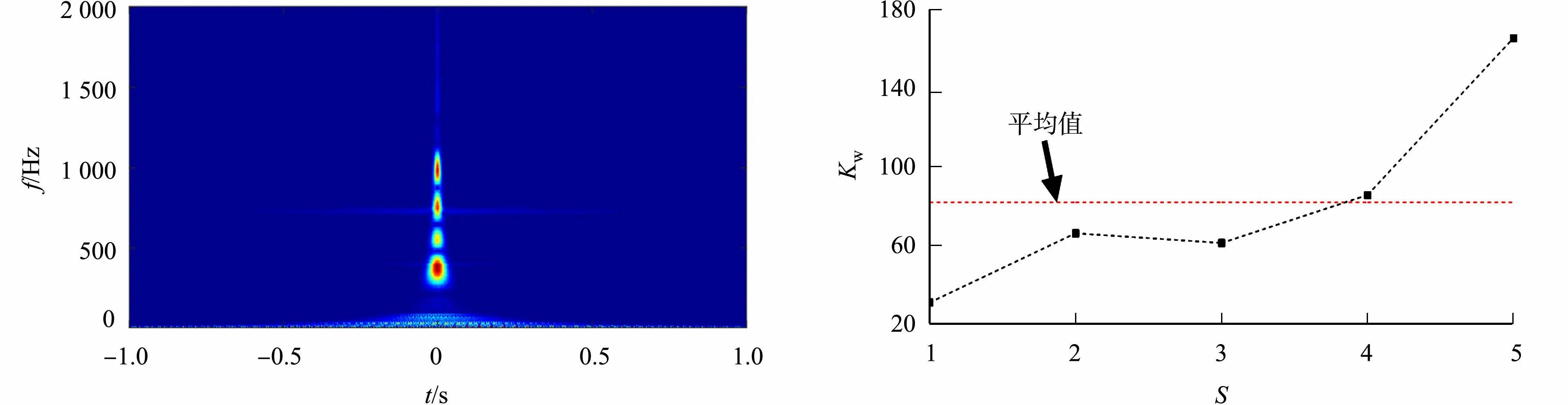
(a) 小波量图 (b) 各阶模态分量的加权峭度值
同样地,对B1工况下钢管混凝土柱有限元模型其余节点的响应信号进行类似处理,即选取各节点信号分量中加权峭度值大于平均值的模态分量进行统计.经统计后可知,大多数节点响应信号中的第3,4,5阶模态分量占比最大,因此,选择第3,4,5阶模态分量进行信号重构.在完成信号重构后,进行TEO计算,并采用FFT对TEO值进行处理.最后,对获得的傅里叶变换系数进行峭度求解和归一化处理,得到钢管混凝土柱有限元模型内部缺陷位置识别结果,如图4(a)所示.
同理,B2,B3,B4工况下的钢管混凝土柱有限元模型内部缺陷位置识别结果,如图4(b)~(d)所示.
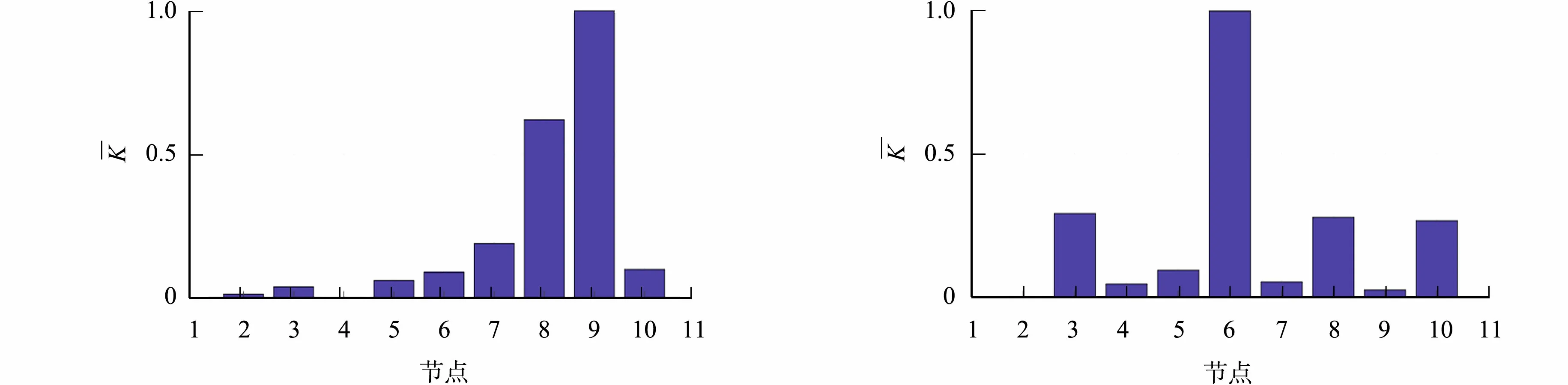
(a) B1工况 (b) B2工况
在对数值模拟和试验结果进行多次统计分析的基础上,建议当某一测点的归一化峭度值超过0.5且表现为大于相邻测点的相应值时,可将其判定为缺陷位置.在对实际工程结构进行缺陷探测时,检测人员可在条件允许的情况下,采用2~3种方法对结构的缺陷位置进行识别和相互验证,这在一定程度上能够防止结构缺陷位置的误判和漏判.
由图4(a)可知:节点9的归一化峭度值超过了0.5的界限,且相对于两侧节点的指标值较为突出,可判定其为脱空位置,这与B1工况十分吻合.由图4(b)可知:节点6处的指标值明显高于其两侧测点的相应值,这表明该处节点附近存在脱空缺陷.由图4(c)可知:节点6,9处的指标值明显大于其两侧测点的相应值且大于0.5,这也说明节点6,9附近发生了脱空现象.同样地,图4(d)中节点3,6,9处的指标值较两侧测点的相应值也偏大,且大于阈值0.5,亦可判定为脱空缺陷位置.
需要注意的是,上述缺陷位置识别过程均是在未知原始未损结构工况信息的情况下进行的,说明文中方法无需预知钢管混凝土结构无损状态下的基准信息,因而具有良好的应用前景.
4 动力试验验证
4.1 钢管混凝土柱试件
为验证所提损伤指标在实际工程结构中的识别效果,以4根现浇带脱空缺陷的钢管混凝土柱试件为研究对象,对其进行动力测试,并对提出的损伤指标进行验证.钢管混凝土柱试件及测点布置,如图5所示.验用钢管混凝土柱的脱空工况,如表2所示.试验模型为现浇钢管混凝土圆形柱,柱长为1 200 mm,直径为150 mm.

图5 钢管混凝土柱试件及测点布置

表2 试验用钢管混凝土柱的脱空工况
首先,将钢管混凝土柱试件沿长度方向分为11等分,并分别设置测点; 然后,采用力锤在单元1和单元2之间施加激励;最后,通过DH5922N型加速度采集器采集加速度时程.由于钢管混凝土柱试件刚度较大且力锤敲击时间非常短,为充分记录到信号特征,设置采样频率为20 kHz,采样时间为2 s.
4.2 钢管混凝土柱试件内部脱空缺陷识别结果
将表2中C1工况下节点6的响应信号作为分析对象,由于其衰减较快,只选取前0.5 s响应数据作为目标信号.首先,对该目标信号进行倒序排列;然后,将节点信号正序排列并组成1个新的信号序列;最后,对其进行复Morlet小波连续变换,得到的小波量图,如图6(a)所示.由图6(a)可知:目标信号的频率主要集中在[0 Hz,500 Hz],[3 000 Hz,4 000H z],[4 400 Hz,4 900 Hz],[5 100 Hz,6 000 Hz],[7 100 Hz,8 500 Hz]这5个频率区间内,因此,判断分量信号的个数为5,然后,采用VMD对其进行信号分解.
C1工况下节点6响应信号的各阶模态分量的加权峭度值,如图6(b)所示.由图6(b)可知:第2~5阶分量的加权峭度值大于平均值,因此,可选择第2,3,4,5阶模态分量进行信号重构.
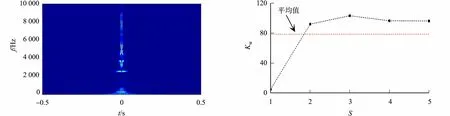
(a) 小波量图 (b) 各阶模态分量的加权峭度值
同样地,对C1工况下钢管混凝土柱试件其余节点的响应信号进行类似处理;然后,选取各节点信号分量中加权峭度值大于平均值的模态分量进行统计分析.经统计后可知,所有节点的分量信号中,第2,3,4,5阶分量占比最大,因此,选择各节点的2,3,4,5阶分量进行重构.在此之后,对重构后的各节点信号进行TEO值计算,并采用FFT进行处理.最后,对经FFT处理的数据进行峭度求解和归一化处理,得到钢管混凝土柱试件内部缺陷位置识别结果,如图7(a)所示.
同理,C2,C3,C4工况下的钢管混凝土柱试件内部缺陷位置识别结果,如图7(b)~(d)所示.
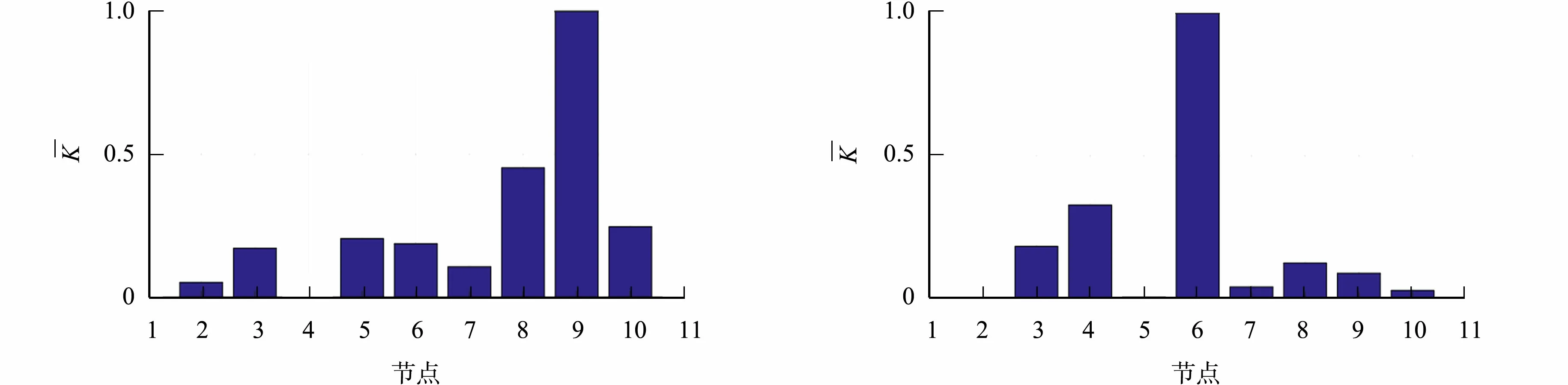
(a) C1工况 (b) C2工况
由图7(a)可知:节点9处的归一化峭度指标值相对于其两侧节点的指标值突出且大于阈值0.5,可判定该节点为脱空缺陷位置,这与C1工况相吻合.由图7(b)可知:节点6附近也存在脱空缺陷.由图7(c)可知:节点6,9处的指标值不仅大于0.5,而且明显大于两侧节点的指标值,可判断这些位置附近发生了脱空现象.由图7(d)可知:节点3,6,9处的指标值均超过0.5且比相邻两侧节点的相应值大,因此,可判断上述位置附近存在脱空缺陷.由此可知,在不依赖于未损工况基准信息的基础上,文中方法能够有效识别钢管混凝土试件的内部脱空缺陷.
值得注意的是,为保证缺陷识别的精准度,在实际工程应用中需在钢管混凝土壁上合理布置测点.理论上,测点越靠近损伤位置时,归一化峭度指标表现出增大的趋势.因此,测点与损伤位置的距离远近只会影响文中方法的精度,但不会从根本上改变文中方法的有效性.若要更加精确地识别钢管混凝土结构的具体缺陷位置,可在归一化峭度值较大的区域加密布设测点.然而,测点越多,检测的成本越高,因此,需要对经济性和精确性进行一个折中,对于较小的试件,以间距0.5~1.0 m为宜.针对实际工程结构,检测人员可以根据自身条件和业主方的要求进行合理的测点布设.目前为止,测点优化布设仍然是一个重要且前沿的研究课题.
5 结束语
为准确探测钢管混凝土试件的内部脱空缺陷位置,从钢管混凝土结构的振动响应出发,提出一种基于变分模态分解与归一化峭度的钢管混凝土柱内部缺陷识别方法.通过钢管混凝土柱有限元模型算例和带脱空缺陷的钢管混凝土柱试件动力试验,对提出的内部脱空缺陷识别方法的有效性和准确性进行验证.研究结果表明:文中方法不但能够有效定位钢管混凝土柱试件和有限元模型的单点及多点脱空缺陷位置,而且不依赖于原始未损工况的基准信息.

