对流扩散方程最优控制问题的重心插值配点格式
黄蓉, 姚梦丽, 翁智峰
(华侨大学 数学科学学院, 福建 泉州 362021)
对流扩散方程描述的最优控制问题被广泛应用于许多领域,如水污染处理[1]、空气污染[2]等.对流扩散方程模拟一个化学或生物过程,涉及的物种相互之间会发生扩散、对流,因此,寻找稳定、高效的数值求解方法具有十分重要的实际意义.目前,许多学者已经提出许多数值求解格式,如间断伽辽金方法[3]、杂交间断伽辽金方法[4]、有限元方法[5-8]、双线性伪谱方法[9]、勒让德-伽辽金谱方法[10-11]、自适应间断伽辽金方法[12]、谱伽辽金近似方法等[13-15].本文主要研究由对流扩散方程控制的最优控制问题.
1 预备知识
设区域Ω∈Rn(n=1,2)是带有利普希茨边界∂Ω的空间有界域.考虑以下无约束最优控制问题,即
(1)
重心插值配点格式广泛应用于数值求解各类微分方程,如平面弹性问题[16]、Volterra积分方程[17]、Allen-Cahn方程[18-19]、Burgers方程[20].重心插值配点格式是一种新型的无网格方法,能以机器精度任意逼近光滑函数,具有操作简单、计算有效、精度高等优势.然而,对重心插值配点格式求解微分方程的研究相对较少.Yi等[21]采用重点插值配点格式求解时间分数阶电报方程,并给出理论分析.文献[22-23]采用重心有理插值配点格式分别求解热传导方程、电报方程,并给出格式的误差分析.Darehmiraki 等[24]基于重心插值配点格式,求解椭圆对流扩散方程的最优控制问题,并证明了配点格式的收敛性.
2 重心插值配点格式
2.1 重心Lagrange插值配点格式
假设存在n+1个互异节点xj,函数f(x)在节点xj处的函数值为fj(j=0,1,…,n).令插值多项式p(x)在节点处成立,p(xj)=fj,根据多项式的唯一性,p(x)可改写为Lagrange插值形式,即
(2)
式(2)中:Lj(x)是Lagrange插值的基函数,满足基函数的性质,有
(3)
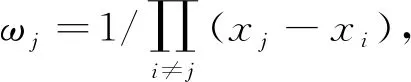
(4)
将式(4)代入式(2),可得
(5)
当p(x)=1时,有
(6)
结合式(5),(6),则重心Lagrange插值公式为
(7)
2.2 重心有理插值配点格式
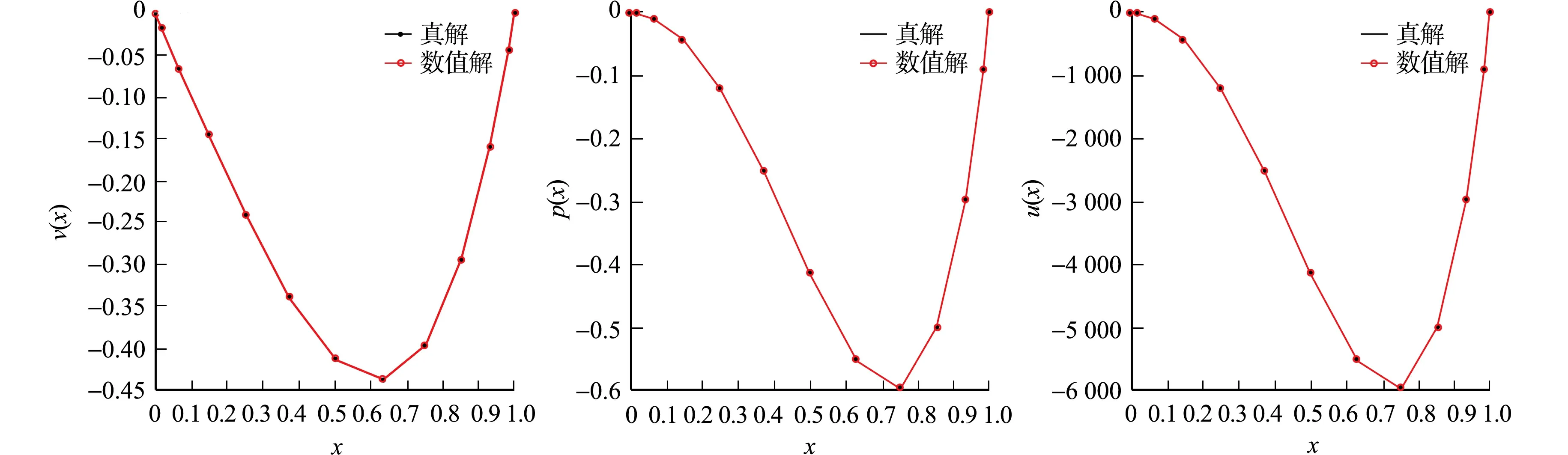
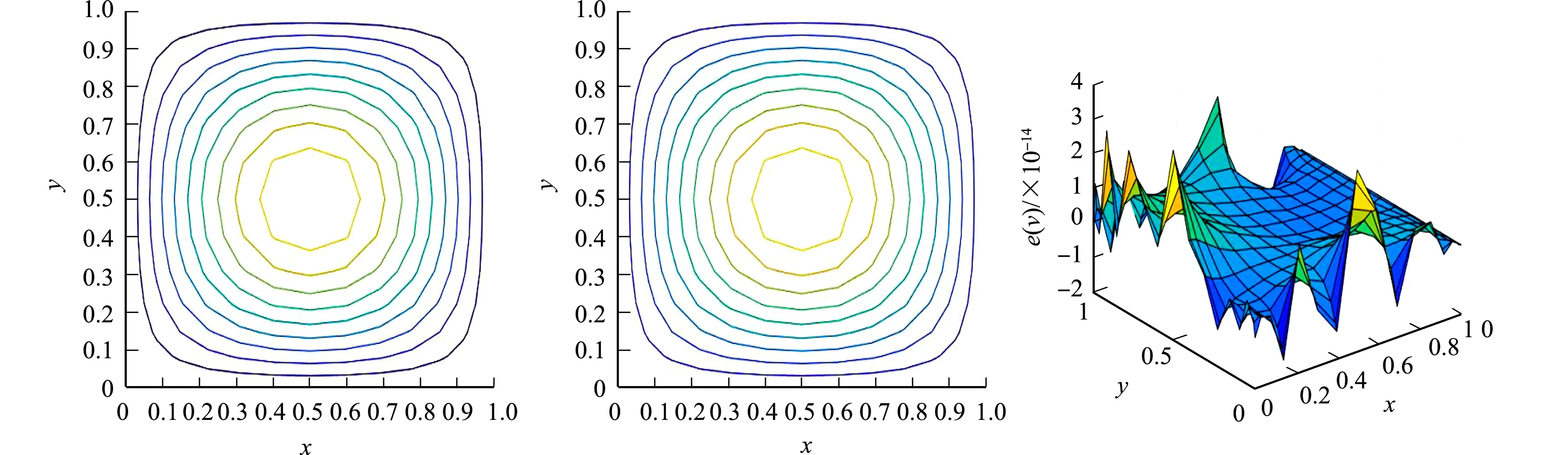
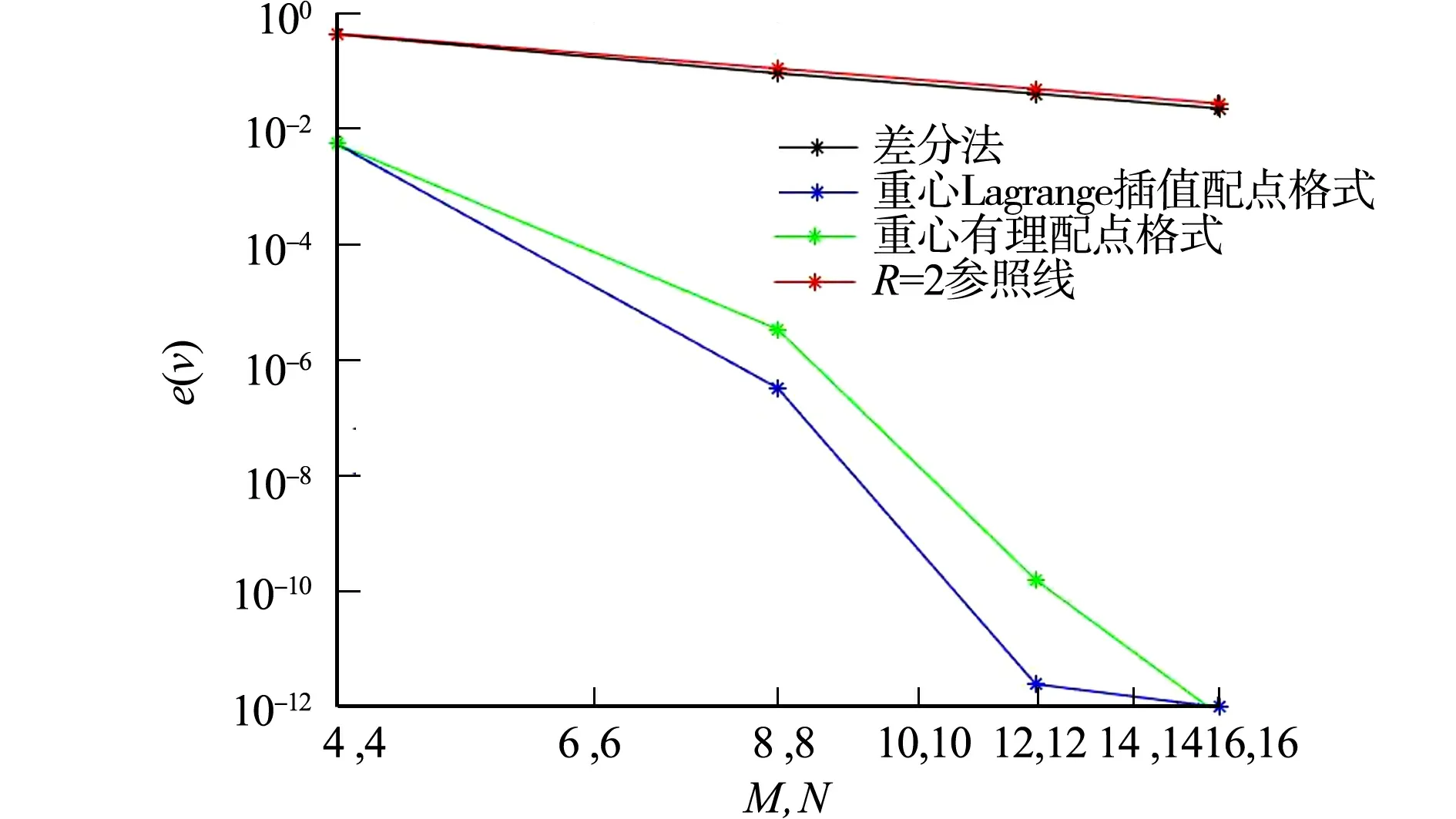
根据一维重心插值配点格式的推导过程,对于定义在区间[a,b]上的函数f(x),给定n+1个插值节点a=x0 (8) 将zk(x)改写为Lagrange插值公式,即 (9) (10) 结合式(8)~(10),重心有理插值公式为 (11) 设p(x)为函数f(x)的重心Lagrange插值公式,则p(x)关于x求导,可得 (12) 针对对流扩散方程最优控制问题,采用Lagrange乘子求导数法,推出最优控制问题的最优性条件.对于最优控制问题(1),定义p为区域Ω上的Lagrange乘子,即 (13) 对式(13)进行泛函变分,对p求Frechet导数,推导得出状态方程,即 (14) 对v求Frechet导数,导出伴随方程为 (15) 类似地,对u求Frechet导数,则最优性方程为 γu-p=0. (16) 将对流扩散最优控制问题转化为代数方程组,即 (17) 采用重心插值配点格式离散方程组,求解对流扩散方程最优控制问题的最优化条件,选取区域Ω=[0,1]×[0,1],α=(α1,α2)T,则化简后的最优控制系统为 (18) 令空间x,y方向的节点分别是M,N,设v(x,y),p(x,y)的重心插值为 (19) 式(19)中:ψi(x),φj(y)分别是空间x,y方向上的基函数;vi,j=v(xi,yj);pi,j=p(xi,yj). 考虑v(x,y)对空间方向变量x,y求k+t阶偏导数,即 (20) 偏导数在节点(xp,yr)处的函数近似值为 (21) 类似地,p(x,y)对空间方向变量x,y求k+t阶偏导数,则偏导数在节点(xp,yr)处的近似值为 (22) 将式(21),(22)代入式(18)中,则对流扩散最优控制系统的重心插值配点格式离散格式为 (23) 式(23)的微分矩阵形式为 (24) 设函数u(x,y)运用重心Lagrange插值法逼近的数值解为pK,S(x,y),误差函数e(x,y)为 e(x,y)=u(x,y)-pK,S(x,y). (25) 重心Lagrange插值公式的逼近性质,如引理1所示. 引理1[21]若u(x,y)∈C(n+1)(Ω),Ω是非空、具有Lipschitz连续边界的开区域,则 (26) 类似地,有 (27) 根据引理1,可得定理1. 定理1设对流扩散方程最优控制问题中的状态变量函数、伴随变量函数分别是v(x,y),p(x,y),且v(x,y),p(x,y)∈C(n+1)(Ω),Ω=[a,b]×[c,d], 数值解分别是v(xk,ys),p(xk,ys),则 (28) 证明:定义线性微分算子D1,D2为 (29) 式(29)对应的离散格式为 (30) 为简化分析过程,仅先分析与状态量函数v(x,y)相关的项,将式(29),(30)相减,可得 D1v(x,y)-D1(xk,ys)=-ε[v(x,y)-vx,x(xk,ys)]-ε[v(x,y)-vy,y(xk,ys)]+ α1[v(x,y)-vx(xk,ys)]+α2[v(x,y)-vy(xk,ys)]- [v(x,y)-v(xk,ys)]=R1+R2+R3+R4+R5. (31) 式(31)中:R1=-ε[v(x,y)-vx,x(xk,ys)];R2=-ε[v(x,y)-vyy(xk,ys)];R3=α1[v(x,y)-vx(xk,ys)];R4=α2[v(x,y)-vy(xk,ys)];R5=-[v(x,y)-v(xk,ys)]. 根据引理1,有 (32) 类似地,可得 (33) (34) 同理,可推得 (35) 文献[22]的定理的推导过程类似定理1,采用重心有理配点格式求解二维最优控制问题的相容性误差,即定理2. 定理2设v(x,y),p(x,y)分别是对流扩散控制问题中的状态量函数、伴随量函数,v(x,y),p(x,y)∈C(n+1)(Ω),Ω=[a,b]×[c,d],v(xk,ys),p(xk,ys)分别是v(x,y),p(x,y)运用重心有理配点格式求解的数值解,则 (36) 式(36)中:C=c·max{ε,α1,α2,(1/γ)},c为常数;h1,h2分别是空间x,y方向的步长. 为便于分析,定义最大相对误差为 (37) 一维、二维的最优控制问题分别采用切比雪夫重心插值配点格式、有限差分法两种离散方法,比较算例的数值结果,验证配点格式的有效性及高精度.对于一维最优控制问题,选取的真解为 v(x)=x(x-1)ex,p(x)=2x2(x-1)ex. (38) 选取区域Ω=[0,1],ε=10-6,α=10-3,γ=10-4,令节点数为M=12,重心Lagrange插值配点格式、重心有理插值配点格式的数值解图,分别如图1,2所示. (a) v(x) (b) p(x) (c) u(x) (a) v(x) (b) p(x) (c) u(x) 由图1,2可知:对于状态量、伴随量、控制量,采用两种重心插值配点格式求解的数值解图均逼近解析解图,表明该数值算法是稳定的. 分别选取ε,α,γ的不同剖分,重心Lagrange插值配点格式、重心有理配点格式、差分法的最大相对误差(e),如表1,2,3所示.状态量的收敛阶(R)对比,如图3所示. 表1 重心Lagrange插值配点格式的最大相对误差(M) 表2 重心有理配点格式的最大相对误差(M) 表3 差分法求解的最大相对误差(M) 图3 状态量的收敛阶对比(m) 由表1~3可知:采用重心插值配点格式求解变量比差分法求解时的误差更小,剖分少量节点,可达到格式高精度.当选取的节点数相同时,采用重心Lagrange插值比重心有理插值求解方程的误差更小.由图3可知:差分法格式的收敛阶是二阶,配点格式满足指数收敛性质. v(x,y)=sin(πx)sin(πy),p(x,y)=π2sin(πx)sin(πy). (39) (40) 选取区域Ω=[0,1]×[0,1],α=(1,1)T,γ=0.5,ε=0.1,令节点数为M=16,N=16,则重心Lagrange插值配点格式、重心整理插值配点格式的精确解、数值解与误差,分别如图4,5所示.由图4,5可知:采用两种重心插值配点格式求解状态量、伴随量的精确解图像与数值解图像逼近,且最大相对误差精度高,可达到10-13量级,表明两种重心插值配点格式均稳定. (a) 状态量的精确解 (b) 状态量的数值解 (c) 状态量的误差 分别选取不同的剖分节点数,重心Lagrange插值配点格式、重心有理配点格式、差分法的最大相对误差,如表4,5,6所示.由表4,5可知:最大相对误差可达到10-11量级,表明两种重心插值配点格式均具有高精度,且前者的求解效果略优于后者.随着剖分变细,3种变量的最大相对误差在逐渐减少.由表6可知:选取M=64,N=64,状态量、伴随量、控制量的最大相对误差分别达到10-3,10-4,10-4量级;与经典的差分法比较,重心插值配点格式选取更少的节点,即可达到更高的精度. 表4 重心Lagrange插值配点格式最大相对误差(M,N) 表5 重心有理配点格式的最大相对误差(M,N) 表6 差分法求解的最大相对误差(M,N) (a) 状态量的精确解 (b) 状态量的数值解 (c) 状态量的误差 状态量收敛阶对比,如图6所示.由图6可知:采用差分法求解方程的收敛阶为2阶;重心Lagrange插值配点格式、重心有理配点格式的收敛阶都呈现指数递减的效果,前者的收敛效果优于后者. 图6 状态量收敛阶对比(m,n) 基于Lagrange乘子法,将对流扩散最优控制问题转化为由状态方程、伴随方程、最优性方程三者联立形成的代数方程组,再分别采用重心Lagrange插值配点格式、重心有理插值配点格式离散求解方程组中的状态量v、伴随量p,并对提出的配点格式进行相容性误差分析.数值实验结果表明,两种重心插值配点格式均具有高精度的特性,选取切比雪夫节点时具有指数收敛的效果.此外,与经典的有限差分格式相比,该配点格式在剖分较少的节点数时,可达到很高的精度.2.3 重心插值配点格式的微分矩阵
3 对流扩散方程最优控制问题的离散格式
3.1 最优性条件
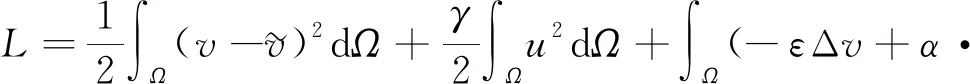
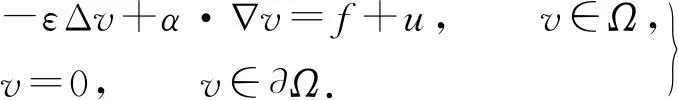
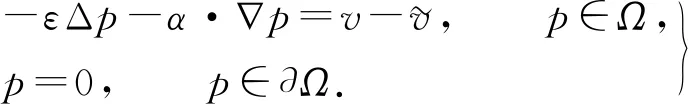
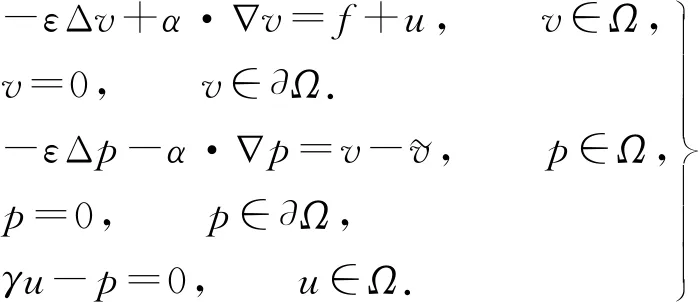
3.2 对流扩散方程最优控制问题的离散格式
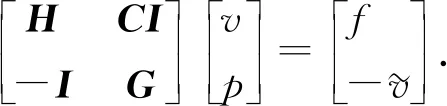
3.3 相容性分析

4 数值算例
4.1 算例1
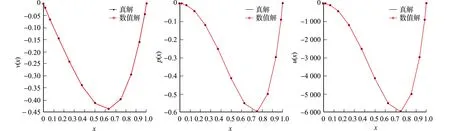



4.2 算例2



5 结束语

