双全纯映射的从属原理及其应用
邵俊霞, 胡春英, 王建飞
(华侨大学 数学科学学院, 福建 泉州 362021)
1 预备知识
记Δ为复平面C中的单位圆盘,即Δ={z∈C:|z|<1}.设X是复Banach空间,Ω∈X为包含原点的区域,若f:Ω→X是双全纯映射,满足f(0)=0,Df(0)=I,其中,I是X中的恒等算子,则称f为Ω上的正规化双全纯映射.记S(Ω)为Ω上的正规化双全纯映射全体.
设GC为单连通区域,记λG(z)|dz|为G上的双曲度量.当G=Δ时,有
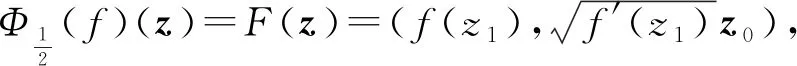
Roper-Suffridge算子可以保持一些重要的解析和几何特征,例如凸性、星形性和Bloch性质等.通过Roper-Suffridge算子可构造出很多星形映射、凸映射和Bloch映射的具体实例[2-11].
2022年,王建飞等[7]利用文献[8]的结果,证明了Roper-Suffridge算子保持ε星形映射,从而得到定理A.


文献[7]进一步给出了更一般的结论(定理B).


星形映射、凸映射和螺形映射等函数类与从属关系具有密切的联系,通过多复变双全纯映射的从属原理,得到螺形映射的性质,需要引入定义1,定义2.
定义1[12-13]设Ω为复Banach空间X中的区域,0∈Ω.F:Ω→X,G:Ω→X为2个双全纯映射,如果存在Schwarz映射V:Ω→Ω,V(0)=0,使得
F(z)=G(V(z)),z∈Ω,
那么称F从属于G,记作FG.

2 相关引理
为了证明主要结果,需要引入引理1,引理2.
引理1[15]设G1C,G2C为两个单连通区域.如果f:G1→G2为全纯函数,那么有
λG2(f(z))|f′(z)|≤λG1(z), ∀z∈G1.
引理2设DC为包含原点的单连通区域,X是以为范数的复Banach空间.如果f:D→D为双全纯函数,f(0)=0,那么有


于是有
这表明F(z,w)∈Ωr(D).
3 主要结果及其证明
主要结果有定理1,定理2.
定理1设DC为包含原点的单连通区域,若f,g∈S(D),则fg在D上成立当且仅当在Ωr(D)上成立.

f(z)=g(v(z)).
由于f,g∈S(D),有v=g-1∘f∈S(D).因为有
从而有
定理2设DC为包含原点的单连通区域,若f:D→C为β型螺形映射,则有



由于f在D上为β型螺形映射,从而有
g=exp(-teiβ)ff.
于是有


应用定理1及gf可知,


推论1设DC为包含原点的单连通区域,Xj是以为范数的复Banach空间,j=2,…,n.若f:D→C为β型螺形映射,则


