数学核心素养测评之小学试题设计
胡典顺 张可心
胡典顺
华中师范大学数学与统计学学院教授、博士研究生导师,华中师范大学数学教育教研室主任,湖北省中学数学教学指导委员会副主任委员;《数学教育学报》《数学通讯》编委,鄂教版高中数学教材(2019年版)副主编,中国国际文化交流基金会第三届“明德教师奖”获得者;曾以访问学者的身份,由国家留学基金委公派访问美国特拉华大学;在《课程·教材·教法》《中国教育学刊》《数学教育学报》《教育科学研究》等期刊上发表论文270余篇,出版《基于数学意义的数学教学改革研究》《整合技术的学科教学知识:从教师专业素养到教师教学实践》《中学生数学素养测评的模型建构与实证研究》等专著,主持多项全国教育科学规划项目和教育部人文社会科学研究规划基金项目。
试题测评法与问卷调查法相结合是数学核心素养测评的常用方法,本文主要介绍试题测评法。根据数学核心素养的测评框架,试题主要围绕核心素养领域、内容领域、情境领域、过程领域四个维度进行测试。由于小学和初中两个阶段数学核心素养的主要表现不同,所以试题设计要注意区分小学和初中的素养表现。本文基于“WJ市义务教育核心素养监测”项目,阐述数学核心素养测评的小学试题设计。
一、设计原则
通过与教育专家、教研员、中小学教师反复研讨,结合国际数学测评的经验及试题开发原则,笔者总结了如下试题设计原则,力求使试题兼具合理性、普适性和有效性:①问题设计必须围绕《义务教育数学课程标准(2022年版)》界定的小学数学核心素养的定义与内涵;②试题表述力求准确、严谨;③试题的情境材料必须来源于生活实践,数据要真实可靠,不出现有关学生成长的负面内容和争议性话题;④同一个情境中的问题设计要区分难度,要包含复合式选择题、封闭式及开放式问答题等,考查的数学核心素养分布合理,各种题型层次分明、分布均匀,以构成一个单元;⑤试题中的每道题都要有题旨和评分标准,以详细说明题目的设计意图、类别划分等。
二、设计思路
数学核心素养测评试题的设计应该以核心素养为导向,准确把握“素养”“内容”“情境”“过程”“问题”要素在命题中的定位与关系。其中,“内容”和“情境”应同时服务于“问题”的提出和解决;“问题”的提出要综合考虑问题解决的思维过程,以把控试题的难度;情境的设计、内容的选择、问题的提出与解决应有利于实现对学生数学核心素养的测试。测评试题由教育专家、教研员、中小学教师负责设计,并从正确性、严谨性、科学性、真实性等方面审核题目。经过多轮筛选、修改后,命题人确定正式试题。笔者以“WJ市义务教育核心素养监测”项目的小学试题设计为例,阐释设计流程。
1.明确试题测评目标
题目的设计,首先要明确测评目标,界定测评内容的边界和水平。本项目中,小学试题的测评对象是四年级学生,测评目标是考查学生数学核心素养的发展情况。设计试题时,要保证测评内容在四年级的知识范围内,符合测试对象的年龄特征和认知水平,且解题过程能够反映被试的数学核心素养表现。
2.编写备选题目
明确测评目标后,接下来就是邀请教育专家、教研员、小学骨干教师等编写备选题目。命制备选题目,需要从不同内容领域、不同情境领域分别出题,题目数量和类型越多越好,可以通过改编经典题目或者结合日常生活创编题目等方式设计。
3.专家审核并筛选题目
请专家审核备选题目可以保证测评工具的内容效度。题目筛选可以从以下几个方面考量:题目类型是否多样化,是否涉及所有内容领域和情境领域;题目难度搭配是否合理,三个过程领域(数学表述、数学运用、数学阐释)的题目比重是否恰当;整套试题难度是否合适,是否涵盖了小学阶段的数学核心素养要素等。
4.形成试题统计表
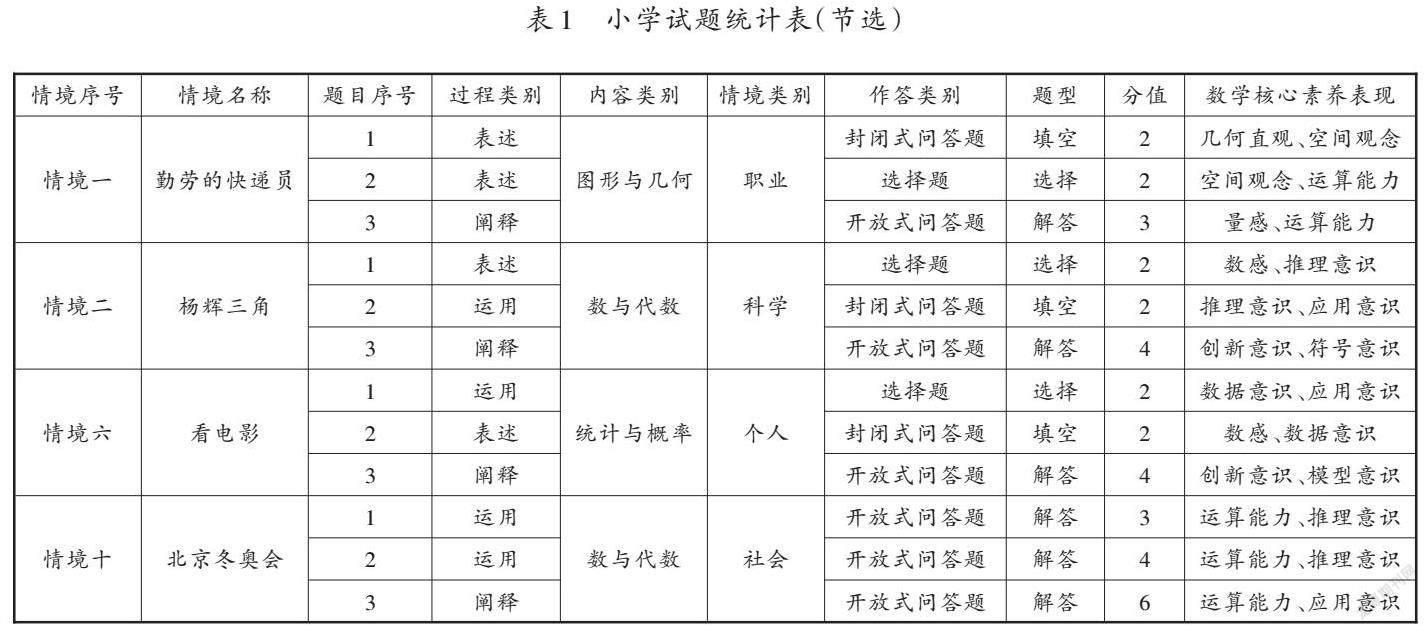
筛选好题目后,要把题目按照合适的顺序进行排列,并根据难度赋分。本项目的小学试题一共有10道,每道题含2~3个小问题,总分为100分。命题人梳理每道题涉及的内容类别、情境类别、过程类别、核心素养表现等信息,形成试题统计表。受篇幅所限,这里仅展示试题统计表的部分内容(见表1,该部分题目的评价模式均为“纸笔作答”)。
表1分别呈现了职业情境、科学情境、个人情境、社会情境下的试题,其中“数与代数”领域2道题,“圖形与几何”领域和“统计与概率”领域各1道题。每个情境包含3个小问题,至少涉及2种过程类别,考查2种核心素养,并且作答类别有差异性。整体来看,题目设置合理,符合设计原则。完成试题统计表后,要统计整套试题各类别题目的分值,以保证各类别试题均有涉及且分值分布均衡合理。
5.预测试、检验与修订试题,确定正式试题
命题人根据试题统计表各类别题目的分值情况,考虑是否需要调整题目分值,或者删改题目;确定所有题目后,严格审查每道题目,确保题目不出现科学性错误、符合被试的认知、情境设置与考查内容密切相关;后续用确定的试题进行小范围的预测试,并对试测结果进行定性和定量分析,进一步修改、完善题目,最终确定正式试题。
三、设计案例
本文仅以表1中4道情境问题为例,展示数学核心素养测评的小学试题。
案例一:勤劳的快递员
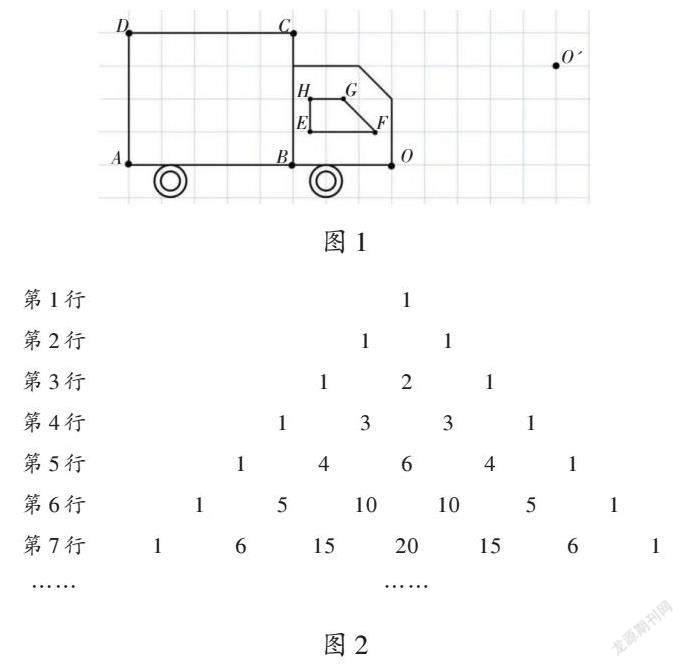
近年来,我国快递行业迅速发展,给人们的日常生活带来了极大便利。快递员的工作就是以较快的速度将特定物品运达指定地点或目标客户手中。某快递员的运输车简图如图1所示。
问题1:图1中车窗(四边形EFGH)的形状是 。
问题2:快递员要把货物送到指定地点(从O点到O'点),按照方格纸界定的路线,正确的平移方式是( )。
A.向右平移5个格子,再向上平移3个格子
B.向右平移3个格子,再向上平移5个格子
C.向左平移5个格子,再向上平移3个格子
D.向左平移3个格子,再向上平移5个格子
问题3:如果方格纸中每个正方形小格子的边长都是1厘米,你能算出车厢(长方形ABCD)的面积吗?
案例一立足职业情境,考查学生对“图形与几何”相关知识的掌握情况。问题1考查学生对四边形的认识,涉及几何直观、空间观念两大素养;问题2考查学生对图形的位置与运动过程的理解,需要学生具备一定的空间观念和运算能力;问题3考查学生对长方形面积公式的掌握情况,此题也可以通过数格子求解,解决方法多样,涉及空间观念和运算能力两大素养。解决问题1和问题2,学生只需要进行“数学表述”,而问题3的解题思维过程为“数学阐释”。
案例二:杨辉三角
杨辉三角是我国数学史上的重要成就。如图2所示,这个看上去平淡无奇的“数字”三角形,却有着很多奇妙甚至神秘的特性等待我们去发现。
问题1:观察杨辉三角中的数字及其规律,你发现第8行数字的个数是( )。
A.6个
B.7个
C.8个
D.9个
问题2:第9行从左往右数第3个数字是______。
问题3:观察杨辉三角中的数字及其规律,说出其中的一条规律。
案例二立足科学情境,考查学生对“数与代数”相关知识的掌握情况。问题1比较简单,考查数感和推理意识,思维过程是“数学表述”层次;问题2考查推理意识和应用意识,涉及“数学阐释”思维过程,学生要先根据已知信息推理出第8行的各个数字,再推理出第9行的数字;问题3是一道开放式问答题,考查创新意识和符号意识,涉及“数学阐释”思维过程,学生根据观察和推理写出一条规律即可。
案例三:看电影
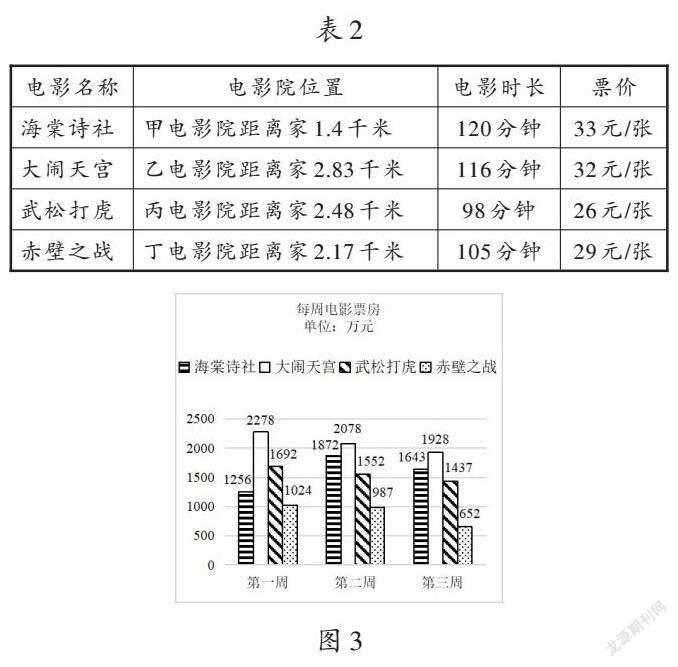
小明计划周末看一场电影,电影的放映信息如表2和图3所示,请根据图表中的信息回答问题。
问题1:请观察表2,小明想去看一场同时满足以下三个条件的电影——电影院距离家不超过2.5千米,电影时长超过100分钟,票价低于30元/张,符合小明要求的电影是( )。
A.海棠诗社 B.大闹天宫
C.武松打虎 D.赤壁之战
问题2:请观察图3,第二周《大闹天宫》的票房是 万元。
问题3:请观察图3,如果按照图中的趋势发展下去,第四周《大闹天宫》的票房估计是多少?请说明理由。
案例三以“看电影”的个人情境引入,主要考查“统计与概率”的相关知识。问题1聚焦数据意识和应用意识,考查学生整理和分析数据的能力,学生需要筛选出符合条件的数据信息作答,涉及“数学运用”思维过程;问题2聚焦数感和数据意识,考查学生对统计图的认识,学生通过识别图中数据信息作答,涉及“数学表述”思维过程;问题3聚焦创新意识和模型意识,学生需要根据已知信息进行建模和推理,涉及“数学阐释”思维过程。问题3属于开放式问题,学生言之有理即可。
案例四:北京冬奥会
2022年2月4日北京冬奥会正式拉开帷幕,继北京2008年奥运会后,奥林匹克会旗时隔14年再次在国家体育场“鸟巢”升起……冬奥会受到国人的高度重视,越来越多的人参与冬季运动……
问题1:2月8日,女子自由式滑雪大跳台比赛在首钢滑雪大跳台吹响号角。经过前面的比赛,暂列前两名的运动员得分如表3所示。
比赛的总成绩是取三轮比赛中成绩最高的两轮比赛分数之和,请问法国选手要想追平中国选手的成绩,则第三轮要拿多少分?
问题2:自由式滑雪大跳台比赛的评分采用百分制,且每位裁判打出的分数都是整数。计分规则是:每位裁判打出分数的平均数为一轮比赛的最终得分。表4是第一轮比赛中五位裁判对运动员小钦打出的分数,但是不小心被污渍覆盖了一部分。已知小钦最终的成绩是79分,请求出被覆盖的成绩。
问题3:冬奥会结束之后,某学校四年级一班的46名学生到北京滑雪场游玩。他们需要坐观光车到山顶,大观光车能坐6人,小观光车能坐4人。如果最多只能租用10辆车,并且刚好坐满(没有空位,所有人都有座位),他们有几种安排方案呢?分别怎样安排?请说说你的想法。
案例四以“北京冬奥会”引入,属于社会情境,考查“数与代数”的相关知识。问题1考查两位小数的加减法,问题2考查平均数的理解及整数四则运算。解决这两道题涉及的思维过程为“数学运用”,考查的数学核心素养为运算能力和推理意识。问题3比较复杂,主要考查运算能力和应用意识,学生求解的方法和过程不唯一,解题思维过程为“数学阐释”。
四、結语
试题测评法是数学核心素养测评的重要方法,试题设计质量直接关系到测评结果。设计试题,首先要考虑测试对象,根据被试的年级确定题目考查范围,不应出现超纲题;其次试题所关注的不是纯粹的数学,而是考查学生在问题情境中所能展示的数学思维品质和解决问题的能力。基于此,试题应该以文字、数据或图表等描述一个真实的问题情境,在不同的问题背景下考查学生几何、代数、统计等知识水平。作答时,学生需要将情境中的信息转化成数学问题,经历数学表述、运用和阐释的思维过程,从而获得数学结论。由此通过试题测评出学生数学核心素养的表现情况。
(张可心系华中师范大学数学与统计学学院硕士研究生)
[专栏文章系教育部人文社会科学研究规划基金项目“中小学核心素养测评的模型建构与实证研究(课题编号:19YJA880012)”、中央高校基本科研业务费项目“新高考分省市命题分学科质量评价指标体系研究(课题编号:CCNUTEI2021-13)”的成果。]
责任编辑 刘佳

