高铁桥式站房结构的车致振动特性研究

张 俊,张丽娜,智国梁,胡文林,郭 彤,王少林

(1. 宿迁市高速铁路建设发展有限公司, 江苏 宿迁223800; 2. 东南大学 土木工程学院, 江苏 南京 210096; 3. 中国铁路设计集团有限公司 城市轨道交通数字化建设与测评技术国家工程研究中心, 天津 300308)

0 引言

近年来,随着我国社会经济的快速发展,高速铁路运输需求不断增长,而列车高速通过车站的情况越发普遍,由此引发的环境振动问题也愈加突出,相关研究表明[1-2],高速列车运行带来的振动影响已成为环境公害的主要影响源之一。在此背景下,为提升旅客候车的安全性与舒适性,有必要对高速列车通行状态下不同类型的铁路站房结构进行振动响应特性研究[3-5]。

此前,国内外学者就车致振动预测方法进行了深入研究。魏鹏勃等[6]通过对地面线路城轨列车引起的自由场地振动进行多参数分析,提出了一种用于预测地面振动的数学模型。BIAN等[7]基于2.5维有限元薄层单元法,推导出了轨道和土体之间的动力耦合分析模型,以此预测了列车运行状态下的地面振动。高广运等[8]利用2.5维有限单元法,对高速列车荷载引起的非饱和路基地面振动进行了研究,结果表明,同一车速下非饱和路基地面振动加速度幅值大于饱和路基。ZENG等[9]基于PEM法对轨道不平顺激励下的高速列车—无砟轨道板—简支梁桥耦合系统开展了随机振动研究,结果显示PEM法相比于MCM法,可以显著节省计算时间,且保证较高的计算精度。ZHANG等[10]提出了一种用于分析“站桥合一”结构的车致振动频域模型,并根据此模型研究了某站房结构的振动特性和减振措施,结果表明,最有效的减振措施是采用道床减振垫和增大柱子截面。

针对站房结构的车致振动问题,学者们也进行了一系列研究。张凌等[11]对列车进出南昌西站时引起的候车层振动进行了现场测试和调研,结果表明,车站结构形式对振动的传递特性影响较大,且振动主要以垂向振动为主。谢伟平等[12]以某典型“桥建合一”型地铁侧式高架车站为工程背景,通过对站房结构振动和噪声的现场测试,分析了这类结构型式的振动响应规律,结果表明“桥建合一”型地铁高架车站相比“桥建分离”型车站的振动响应更大,其中候车层的峰值加速度约为后者的2～6倍。王祥秋等[13]对高铁沿线的地面与建筑物振动进行了实测,结果显示列车以270 km/h速度行驶时,振动频率主要集中在25.0～60.0 Hz,建筑物的Z振级最大值为70.6 dB。巴振宁等[14]对铁路站台处的振动进行了现场实测,研究了不同车速下两车交汇行驶时的振动特性,验证了振动反弹区的存在。朱志辉等[15]采用有限元法建立轨道-客运站三维耦合动力分析模型,对天津西站站房结构进行了模态分析和振动响应分析,研究发现客运站结构的振动主要由列车竖向动力荷载所控制。方联民等[16]采用虚拟激励法和有限元法建立了车辆-轨道-车站耦合的垂向随机振动模型,研究了天津西站不同区域和楼层的振动特性,得到了不同车速下车致振动响应规律。李正川等[17]通过数值仿真研究了成渝高铁沙坪坝站的车致振动响应特性,研究表明车速仅影响振动响应的大小,不改变其振动规律,同时指出减振设计时应重点关注40 Hz左右的振动。裴强等[18]通过建立土-结构三维有限元模型,计算了不同距离下结构各层的振动响应,结果表明,结构的振动随着距离的增加而逐渐衰减,在相同的距离处,楼层的竖向振动幅值随着楼层的高度增加而增加。

针对高架车站结构,上述研究主要采用数值模拟或现场测试的方式进行研究,其分析方式相对单一,且缺乏对振源荷载的理论分析和应用。文中以高铁车站主要类型之一的桥式站为研究对象,依托某实际车站工程,首先对振源荷载进行了理论求解,然后通过数值模拟和现场测试相互印证的方式,系统研究了列车高速通行状态下的结构振动特性,最后对候车层和站台层的振动舒适度进行了评价,相关研究成果可为新式高架车站的减振设计提供参考。

1 工程概况

文中所研究的车站南北向450 m,东西向83.1 m,站内设2台6线(其中正线2条,到发线4条)。站房建筑釆用线下桥式站型设计,最高接待人数可达1 000人,由进站集散厅、售票厅、候车厅、出站厅等客运服务设施组成。在结构体系上,采用桥式站房设计,正线部分为高架桥结构且承轨层与站台结构相分离。车站站房总建筑面积为3 999 m2,属于中小型车站,其正线局部剖面图如图1所示。

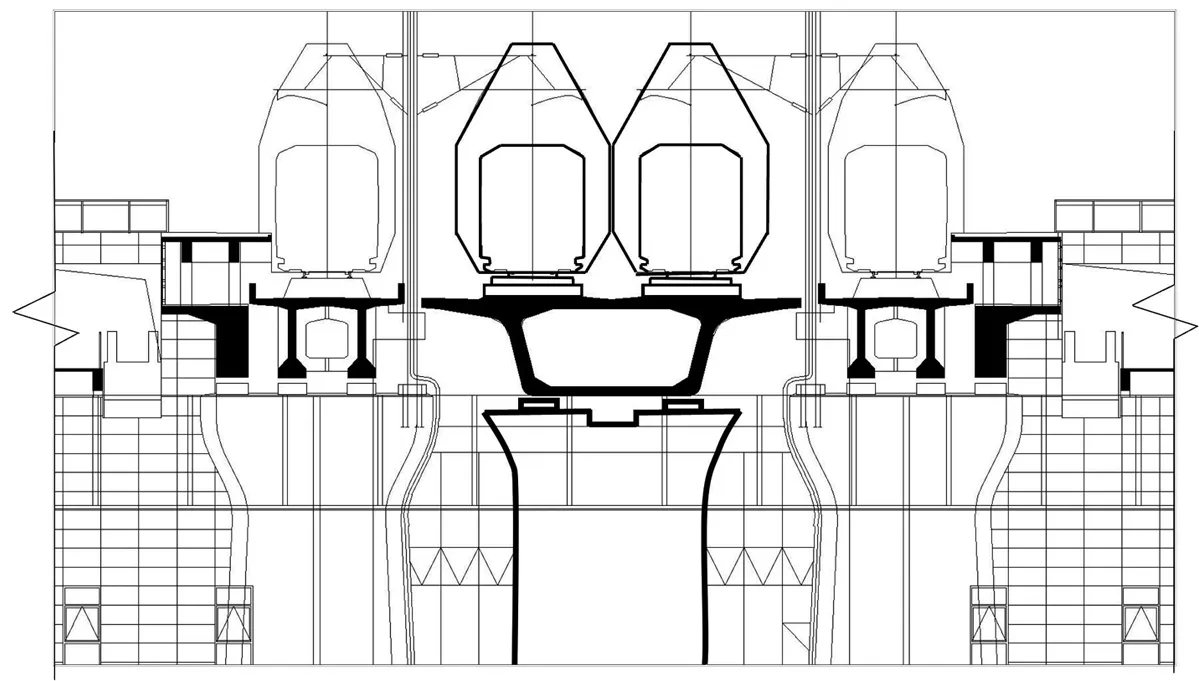
图1 车站正线局部剖面图Fig. 1 Sectional view of the main line of the station

2 振源荷载研究

对车站结构进行车致振动分析时,首要确定的是振源荷载。考虑到列车运行的动态性与车轨系统的复杂性,文中采用数值方法单独计算列车-轨道系统,求得系统的轮轨力,并作为振源荷载输入到站房结构有限元模型中,进而对站房结构各分区进行振动分析。

2.1 列车-轨道动力学模型

2.1.1 列车动力学模型

文中所研究的桥式车站作为客运车站,通行列车均为客运列车,因此综合考虑四轴客车的结构特点以及列车各系悬挂的非线性来确定列车动力学模型。此外,在车轨耦合系统中,纵向耦合作用通常较弱,因此本研究采用二维列车-轨道模型,只考虑列车的垂向和横向运动[19],即车厢的沉浮和点头运动,2个转向架的沉浮和点头运动和4个轮对的垂向运动,共计10个自由度。车轨模型如图2所示,相关参数见表1。

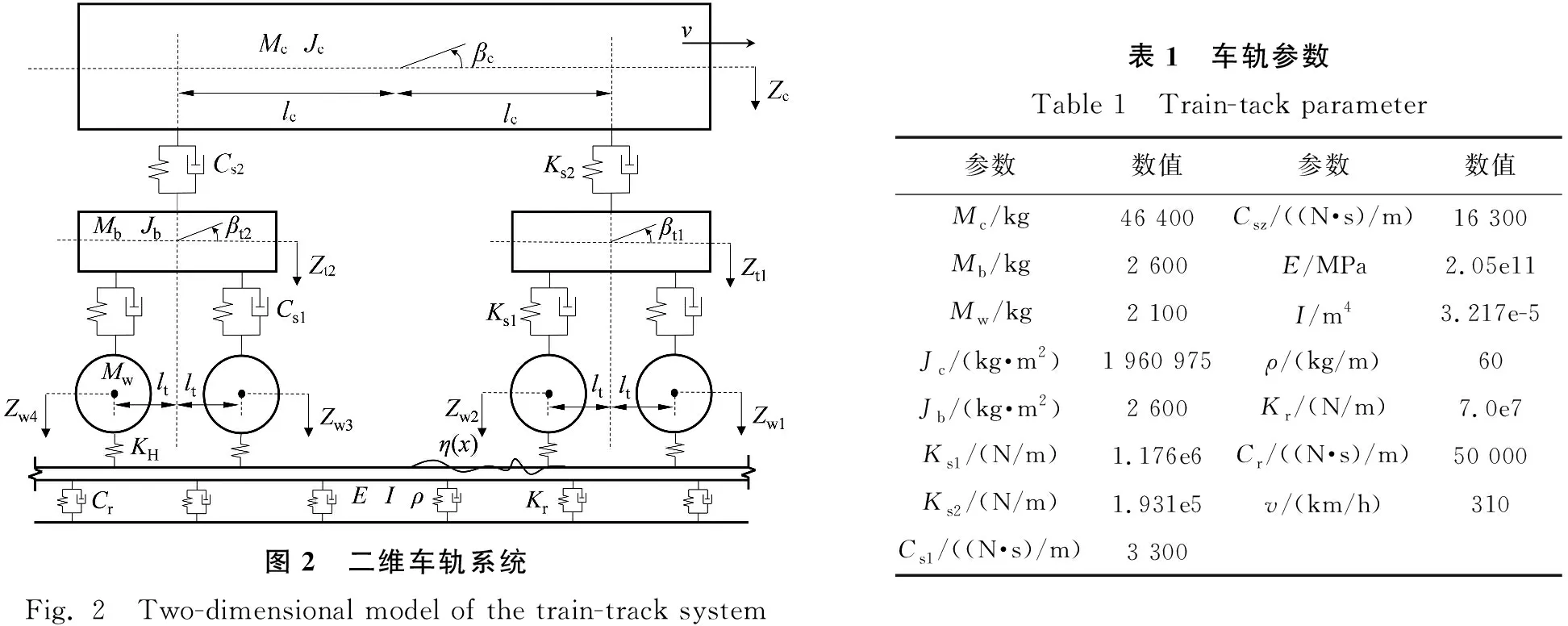
图2 二维车轨系统Fig. 2 Two-dimensional model of the train-track system表1 车轨参数Table 1 Train-tack parameter参数数值参数数值Mc/kg46 400Csz /((N·s)/m)16 300Mb/kg2 600E/MPa2.05e11Mw/kg2 100I/m43.217e-5Jc/(kg·m2)1 960 975ρ/(kg/m)60Jb/(kg·m2)2 600Kr/(N/m)7.0e7Ks1/(N/m)1.176e6Cr/((N·s)/m)50 000Ks2/(N/m)1.931e5v/(km/h)310Cs1/((N·s)/m)3 300

列车动力学方程基于Lagrange运动方程建立,表达式为:

(1)

式中:EK为系统的总动能;EP为系统的总弹性势能;ED为系统的总耗散能;qi为q的第i个元素,定义为:

(2)

式中:qc=[Zcβc]T为车厢的沉浮和点头运动;qt=[Zt1βt1Zt2βt2]T为转向架的沉浮和点头运动;qw=[Zw1Zw2Zw3Zw4]T为4个轮对的垂向运动。

将系统的总动能EK、总弹性势能EP和总耗散能ED代入式(1),得到10个方程,写成矩阵的形式:

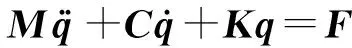
(3)

式中,F包括列车自重和轮轨接触力。

2.1.2 轨道动力学模型

文中所涉及的车场均采用无砟轨道,自上而下包括钢轨、轨道板和底座板。在轨道动力学模型中,将钢轨视为支撑在轨道板上的有限长Euler-Bernoulli梁,扣件简化为一系列并联的弹簧-阻尼元件,轨道板和底座板视为刚体[20-21]。因此,钢轨的运动方程为:

(4)

式中:u为钢轨的竖向变形;Kr和Cr分别为扣件的刚度和阻尼;δ(·)为Dirac函数;Pi为第i个轮对与钢轨的接触力,由2部分组成: 第1部分是移动静载; 第2部分是由于不平顺产生的动力分量。

2.1.3 轮轨相互作用动力学模型

文中综合考虑轮轨接触的动态几何特性,采用迹线法进行计算,其中轮轨接触力Pi可以根据Hertz接触理论计算:

(5)

式中:u,a和η分别为钢轨、车轮的位移和轨道不平顺数值;下标wi为第i个车轮所对应的数值。文中车轮采用磨耗型踏面,G取3.86R-0.155×10-8m/N2/3,其中车轮半径R=0.46 m。

最后,将上述确定的轮轨相互作用力分别以车轮反作用力、轨道外荷载的形式代入列车动力学模型和轨道动力学模型中,即可进行后续的求解。

2.2 轨道不平顺激扰模型

对于轮轨系统而言,轨道不平顺是引起激扰的主要原因。文中选取德国低干扰(高速铁路)轨道不平顺功率谱,波长范围2～120 m。根据频域功率谱的等效算法,分别求出频谱的幅值和随机相位,进而通过傅立叶逆变换得到轨道不平顺的时域模拟样本,如图3所示,其轨向、高低不平顺幅值分别介于±4 mm和±7 mm之间。

图3 轨道不平顺时域样本Fig. 3 Time-domain samples of track irregularity

2.3 振源荷载计算

在进行振源荷载计算时,列车选取CRH3型动车组列车,轨道结构选用CRTS-Ⅲ型无砟轨道。根据本课题组前期经过实测验证的研究成果[22-23],采用迭代算法的改进算法对列车-轨道动力学模型进行求解,这种算法的思想是以单个接触力的迭代计算替代接触力向量的迭代计算,具体求解流程如图4所示。此外,在求解时时间步长根据奈奎斯特频率进行确定,即Δt=1/2f≤1/2×1 000≤5×10-4s,其中f代表轨道的最大振动频率;将求解得到的轮轨力时程函数作为有限元模型的输入荷载,在对应线路的每一个扣件点上输入对应的轮轨力时程函数,再进行后续动力分析。图5为列车速度310 km/h时,轨道某一扣件处的轮轨力,其数量级和振动频率与文献[24-26]结果一致,说明文中振源荷载计算方法具有可靠性,满足后续的振动预测要求。

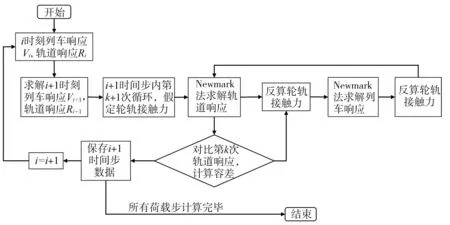
图4 车轨耦合模型计算流程图Fig. 4 Calculation flow chart of train-track coupling model

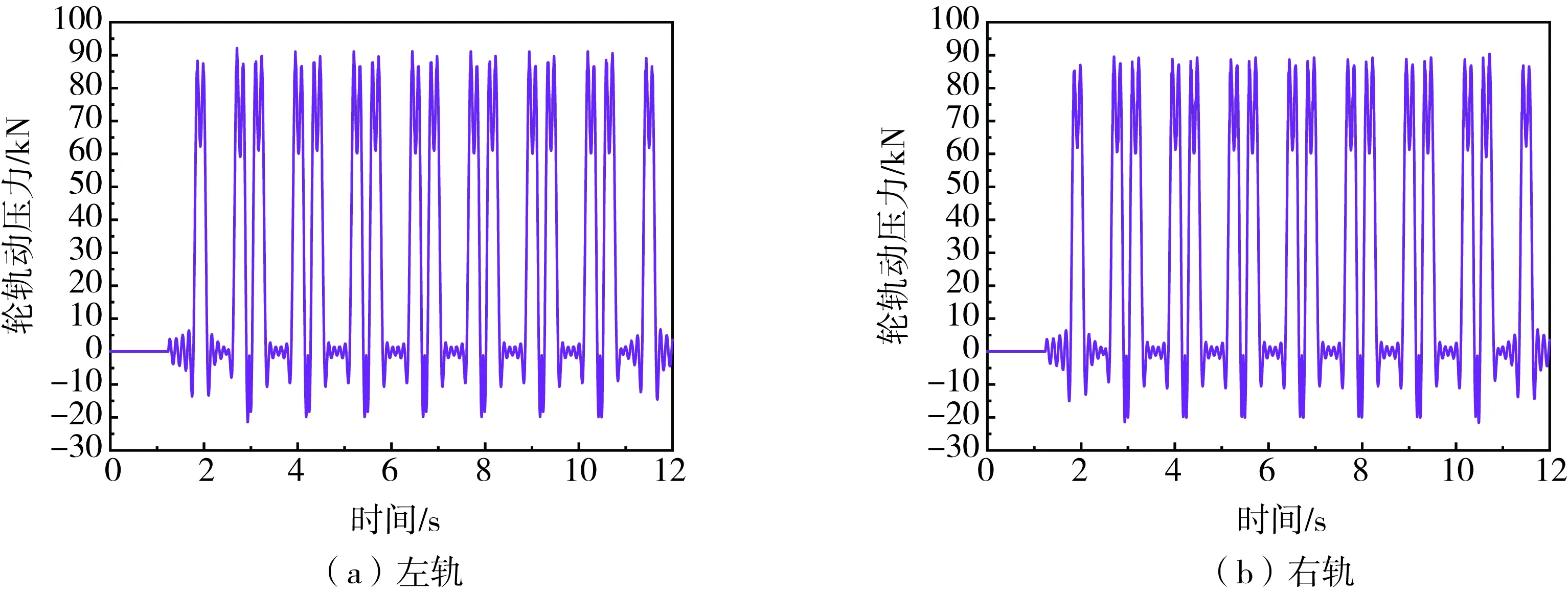
图5 左、右轨道某一扣件处的轮轨力Fig. 5 Wheel-rail force at a fastener on the left and right tracks

3 振动评价方法与标准

3.1 站房振动评价方法

对于振动加速度信号,在频域内采用Z计权振动加速度级进行1/3倍频程分析,根据国际标准ISO 2631[27],铅垂向Z振级VLZ计算公式为:

(6)

式中:a为振动加速度有效值,m/s2;a0为基准加速度,a0=10-6m/s2。

在确定Z振级时,振动加速度有效值a采用计权均方根加速度,计算公式为:

(7)

式中:aw(t)为瞬时频率计权加速度,m/s2;T为振动测量的平均时间,s。

3.2 站房振动评价标准

当前国内外对于铁路站房结构尚无统一的振动评价标准,文中采用GB 10070—88《城市区域环境振动标准》[28]对桥式车站列车高速通行状态下的振动舒适度进行评价。该标准以铅垂向Z振级VLZ作为评价指标,相关指标如表2所示。

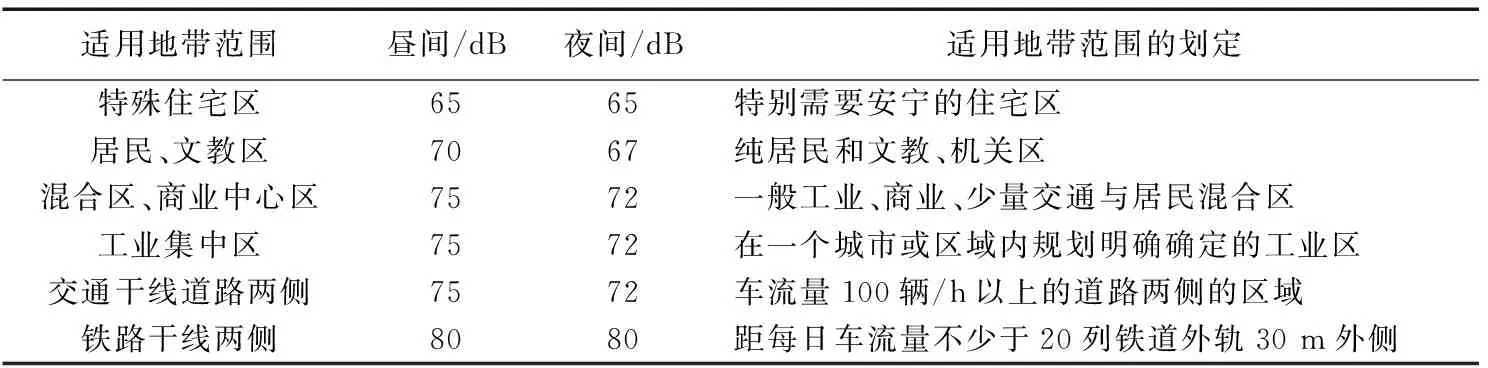
表2 城市各类区域铅垂向Z振级标准值Table 2 Standard value of vertical Z vibration level in various areas of the city

文中针对桥式车站候车层和站台层进行振动响应分析,由于这2个区域距振源距离以及旅客逗留时长均有较大差异,因此对这2个区域分别选用不同的振动限值。对于候车层,由于夜间时段站内旅客并无睡眠需求,参照混合区、商业中心区,Z振级限值昼间和夜间均取为75 dB;对于站台层,由于其距振源较近,振动响应较大,且旅客振动暴露时间较短,参照铁路干线两侧,Z振级限值取为80 dB。

4 站房的振动分析

4.1 有限元建模

文中选取候车层及相对应的站台层和屋盖结构进行建模。建模区域南北长145.2 m,东西宽83.1 m。候车厅位于整个车站结构地上一层。

车站有限元模型(见图6)基于Midas/Civil平台,采用软件自带的梁单元对梁、柱结构进行模拟,楼板结构亦是如此,其中桥墩结构和柱结构采用C60混凝土与Q390钢,梁结构采用C40混凝土与Q345钢,桥墩结构形式为重力梁式,柱结构和梁结构截面均为矩形。楼板结构厚度为0.2 m,按梁格划分板块,材料采用C40混凝土,局部采用C50混凝土。针对轨道结构,钢轨采用梁单元进行模拟,轨道板和底座板采用板单元进行模拟,扣件、CA砂浆层等层间结构采用一维的弹簧—阻尼单元进行模拟,钢轨的型号为60 kg/m,轨道板厚度为0.2 m,底座板厚度为0.5 m,材料选用C60混凝土。

文中在建模时,结构中的梁构件与柱构件的连接方式为刚接,结构整体不考虑土-结构相互作用,由于桥式车站桥梁结构与站房结构之间没有硬连接,为了模拟经地面候车层传递的振动,文中参照常规楼板的材料几何参数,在地面层设置一定厚度的C40混凝土板(如0.3 m)进行以传递振动,一层柱与地面混凝土板采用刚接方式进行连接。

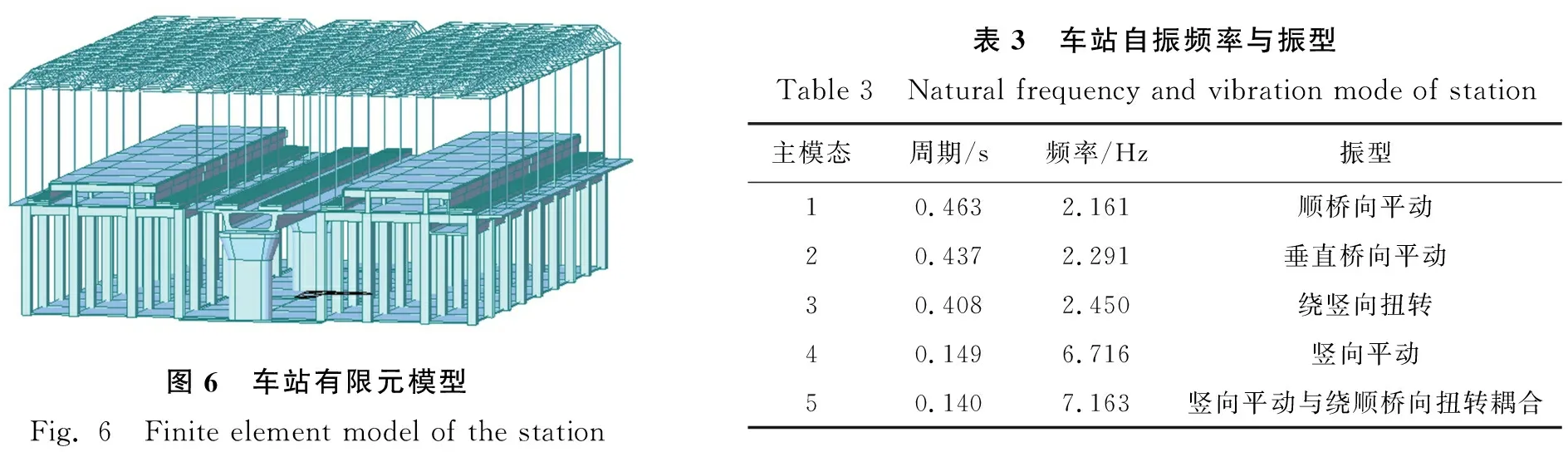
图6 车站有限元模型Fig. 6 Finite element model of the station表3 车站自振频率与振型Table 3 Natural frequency and vibration mode of station主模态周期/s频率/Hz振型10.4632.161顺桥向平动20.4372.291垂直桥向平动30.4082.450绕竖向扭转40.1496.716竖向平动50.1407.163竖向平动与绕顺桥向扭转耦合

4.2 动力特性分析

桥式车站与其他车站型式不同,具有明显的空间效应,结构在顺桥向、横桥向和竖向3个方向上的刚度、质量差异比较大。因此有必要对其进行模态分析,求得结构的自振频率与振型。文中采用Lanczos法对特征值与特征向量进行求解,选取前5阶振型进行分析,如表3所示。

4.3 结构振动分析

4.3.1 分析情况设置

站台层L3、L4为正线车道,车速较高,鉴于此,文中重点针对正线单车道(L4车道)列车以310 km/h通行时的工况,模拟了站台层和候车层的振动响应。其中,候车层的响应点为C1和C2,站台层的响应点为C3和C4,其相距中心线的距离分别为0、25、12、20 m,如图7所示。

图7 振动响应点位置示意图Fig. 7 Locations of vibration response points

4.3.2 结构振动分析

当列车以310 km/h的速度行驶时,响应点C1、C2、C3和C4的垂向加速度时程如图8所示,对应的峰值分别为-0.15、0.03、-0.15、0.12 m/s2。

由图8可知,当列车以310 km/h的速度在L4线通行时,靠近列车行车线路的站台层(C3响应点)振动响应最大,约为C2响应点的5倍,C1响应点振动水平与C4响应点相当,但均低于C3响应点。此外,由于C1响应点在平面上临近行车线路L4,C4响应点在平面上距行车线较远,但二者加速度水平相当,这说明桥墩结构可有效地降低振动响应水平。对比C1和C2、C3和C4响应点可知:在水平方向,站房结构车致振动水平与距行车线距离的远近有关,距行车线越远,振动水平成倍的衰减,其中对于候车层,C2响应点相比C1响应点振动水平减小了4～5倍;对于站台层,C4响应点相比C3响应点振动水平减小了40 %左右。在竖直方向,整体而言,候车层的2个响应点加速度水平明显小于站台层。此外,桥式车站由于其特殊的结构形式,振动波主要有2条传播途径:一是振动通过轮轨系统,沿着桥墩结构进行传递;二是通过站台短柱传递到轨道层,进而通过结构柱传向地面候车层。具体响应点处的加速度水平不仅受振源波的影响,而且也受结构构件的影响。C1响应点位于桥墩附近,其振动波主要是由桥墩结构进行传递;对于C2响应点,其振动响应主要有2个来源:一部分来源于桥墩底部,沿着地面板传递到C2点;另一部分来源于站台处,沿着结构梁、柱传递到C2点。根据图8所示结果,虽然C2点振动波来源广,但是其振动响应依旧较小,这从侧面反映了结构梁、柱、板可有效降低结构的振动水平。

通过Matlab编程,将C1～C4这4个响应点处的加速度时程数据进行傅里叶变换,得到相应的频谱分析曲线,如图9所示。

图9 响应点加速度频程曲线Fig. 9 Response point acceleration frequency curves

由图9可知,对于候车层,响应点C1的主频率主要分布在10 Hz以下,同时在40 Hz左右出现次高峰。由4.2节可知,站房结构第四阶振型(竖向平动)的振动频率为6.72 Hz,与C1响应点主频率(10 Hz以下部分)相一致,这表明列车在L4线通行时,所诱发的振动响应沿着桥梁结构竖向传播,在传播过程中与激起的结构构件波存在一定的耦合作用。响应点C2的主频率主要分布在25 Hz附近,局部略有浮动。从C1点到C2点,振动响应低频部分先于高频部分出现衰减,这是由于地面混凝土板刚度比较大,会产生一定的滤波作用,在振动传递过程中低频振动波大幅衰减所导致的。总体而言,候车层振动属于低频振动,振动频率主要位于15～50 Hz之间。对于站台层,响应点C3和C4的主频率均在40 Hz左右,其频率特性没有候车层丰富,整体趋势比较一致,振动频率主要位于20～60 Hz之间,属于低频振动。此外,振动由C3点向C4点传播时,在6 Hz附近,由于振动波与站台板的耦合作用,C4点的振动有明显的放大,但从全频段来看,仍低于C3点的振动水平。

4.4 实测验证与舒适度评价

为了验证车站有限元模型求解的正确性,文中选取与响应点相同位置的4个测点进行现场测试,测点位置与测试工况与4.3节一致。测试仪器采用朗斯加速度传感器和B&KNOTAR便携式数据采集仪,对各测点实测振动数据进行80 Hz低通滤波处理,一定程度上剔除本底振动的影响,求得各测点1/3倍频程中心频率对应的Z计权振动加速度级,与模拟值进行对比,结果如图10所示。

图10 各测点Z计权振动加速度级对比Fig. 10 Comparison of Z-weighted vibration acceleration levels of each measuring point

由图10可知,Z计权振动加速度级模拟值在各频率段几乎均小于实测值,但整体趋势吻合良好。模拟值与实测值的加速度时程峰值和总振级值对比结果列于表4中,可以发现,加速度时程峰值和总振级值均为模拟值略小于实测值,这可能与模型简化处理、列车荷载取值、荷载施加方式等因素相关,但整体相差不大,说明本文振源荷载以及模拟数据比较准确,所得规律较为合理。

表4 车站测点实测值与模拟值对比Table 4 Comparison between the measured and simulated values of the station

根据第3.1节所述的振动计算方法和第3.2节所述的振动评价标准,选取候车层的振动限值为75 dB,站台层的振动限值为80 dB。由表4可知,候车层的总振级最大值为61 dB,站台层的总振级最大值为74 dB,二者均满足振动限值,但对于站台层而言,其总振级最大值已接近限值。此外,由图10可知,4个测点的Z振级均在30 Hz左右达到最大值,且数值较大,因此在实际工程应用中应重点关注此频段的振动响应,必要时可采取相应的减振措施进行减振处理。

5 结论

1)当列车以310 km/h的速度在桥式车站正线单线通行时,靠近列车行车线路的站台层振动响应最大,加速度峰值为-0.15 m/s2,约为候车层进站口处(C2响应点)振动响应的5倍。此外,在水平方向上,站房结构车致振动水平与距行车线距离的远近有关,距行车线越远,振动水平成倍的衰减,其中对于候车层,C2响应点相比C1响应点振动响应减小了4～5倍。站台层C4响应点相比C3响应点振动水平减小了40 %左右;在竖直方向上,由于桥式车站特殊的结构形式,行车线下方对应候车层处(C1响应点)的振动水平衰减并不明显。

2)列车高速通行引起的站房结构振动以低频为主,振动频率主要位于20～60 Hz之间,站台层的主频率在40 Hz左右,候车层的主频率在0～20 Hz之间。此外,车致振动波在竖向沿桥梁结构进行传播时,与激起的结构构件振动波相耦合,致使候车厅响应点C1频率特性丰富,在40 Hz左右出现次高峰,振动响应较大。

3)通过对车站结构的振动响应进行实测,得到各测点的峰值加速度和1/3倍频程中心频率对应的Z计权振动加速度级,并与模拟数据进行了对比。结果显示加速度时程峰值和总振级值均为模拟值略小于实测值,但整体相差不大,满足舒适度指标限值。证明了文中振源荷载以及有限元模型的可靠性,可为后续相关站房结构振动分析与减振设计提供参考。