纵墙开洞的砌体结构抗震性能多因素分析

张望喜,田 慧,吴 昊,李 勃,史佳佳,易伟建

(1. 湖南大学 土木工程学院,湖南 长沙 410012; 2. 湖南大学 工程结构损伤诊断湖南省重点实验室,湖南 长沙 410012)

0 引言

通过唐山大地震[1]、汶川地震[2]等历次震害统计资料可以发现,在地震中破坏最为严重的是砌体结构房屋,而砌体房屋的纵墙开洞口数量和尺寸远高于横墙,纵墙破坏尤为突出,可能造成大量的人员伤亡和财产损失。

针对砌体结构抗震性能,研究人员做过很多试验研究和数值模拟分析。史庆轩等[3]对窗洞尺寸不同的砌体开洞纵墙进行了低周反复荷载试验,对在不同措施下的多孔砖墙片抗震性能进行了对比分析;薛彦涛等[4]对缩尺1/2的砖砌体墙片开展拟静力试验,探究在墙片局部配置构造柱与配筋条带的构造措施对其抗震能力的影响;MISTLER等[5]利用ANSYS对典型砌体结构模型进行了抗震性能评估;张荣[6]使用AlgorFEA程序对顶部作用水平力、开洞大小及位置各不相同的数十个砌体墙进行计算,探讨了开洞位置对墙片刚度的影响;金德保等[7]采用底部剪力法分析了砌体房屋内纵墙开洞大小与地震剪力的关系,研究了其对房屋抗震性能的影响;NAKAGAWA等[8]对大比例砌体结构开展单向拟动力试验,研究砌体房屋遭遇强震后的倒塌特性;PARISI等[9]利用有限元软件分析研究不规则素砌体墙片的抗震性能;吴会阁等[10]以不同开洞情况为前提,对加气混凝土砌块和构造柱组合墙体的抗震性能进行了研究;田颖等[11]利用ABAQUS对喷涂聚氨酯弹性体砖砌体墙建立有限元模型,研究了用聚氨酯加固的黏土砖砌体墙的抗震性能。

在相似的外部环境条件下,结构破坏或倒塌的本质原因还是在于建筑物本身的抗震性能,外部环境条件不可轻易改变,但结构设计却是人为完成的,故可以由优化结构设计来保证建筑物的抗震性能。但是影响砌体墙抗震能力的原因有很多,为了探究不同因素影响下带有开洞纵墙的砌体结构抵抗地震作用的能力,文中在进行结果比较与参数验证的前提下,使用ABAQUS软件,建立了17个开洞纵墙墙片模型与系列考虑不同构造措施与房屋高度的整体结构模型,分析中部构造柱、混凝土水平系梁、窗端柱等构造措施,以及构造柱配筋率、开洞率和开洞方式等因素的影响,之后对构造措施不同布置情况下多层砌体结构的适用烈度和高度进行了讨论。

1 数值模拟及参数验证

1.1 模型及参数

图1 墙片几何尺寸Fig. 1 Dimension of walls

表1 墙片设计参数Table 1 Design parameters of walls试件编号柱截面/mm纵筋箍筋含柱率/%柱配筋率/%ZQ1—————ZQ3120×2404146@15020.02.1表2 材料的实测抗压强度Table 2 Measured compressive strength of material类型砖块砂浆混凝土平均抗压强度/MPa19.88.926.1

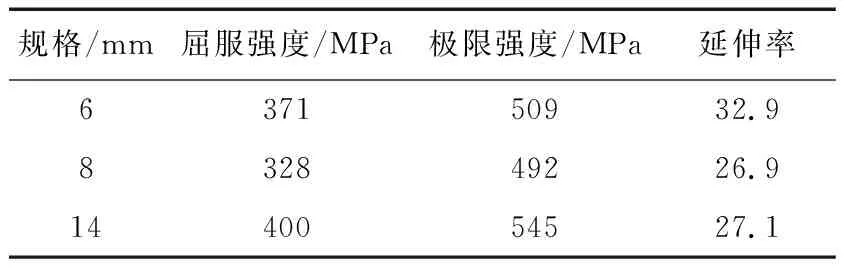
表3 钢筋的材性试验结果Table 3 Material property test results of rebar

文献[13]使用ABAQUS软件创建有限元墙体模型,材料使用混凝土损伤塑性模型,砌体本构关系使用杨卫忠模型[14],混凝土及钢筋本构则使用现行规范[15]。单元选取实体单元,砌体与混凝土使用C3D8R单元,钢筋使用T3D2单元,钢筋单元边长取50 mm,混凝土、砌体单元边长取120 mm 。砌块和砂浆之间使用整体式的建模方式,钢筋和混凝土使用分离式建模方式,且使用Embed连接。混凝土质量密度为2 500 kg/m3、钢筋质量密度为7 800 kg/m3、砌体的质量密度为2 000 kg/m3。分析时在墙片模型顶部采用水平位移加载,每一级加载时间间隔不变,位移增量为0.5 mm。

1.2 模拟与试验结果对比

墙片模型有限元分析结果与试验结果的对比见表4。

表4 墙片的数值模拟结果和试验结果对比Table 4 Comparison of numerical simulation and test results of walls

根据文献[9]破坏荷载取为荷载下降到极限荷载的60%,以荷载-位移曲线出现的明显拐点视作开裂点。由表4表明,模型的计算值与试验实测值差距很小,故认为模拟结果较为符合真实试验结果。

图2与图3为等效塑性应变云图与实际墙体破坏的对比图。模型的破坏主要是沿对角线方向,但可以看到,其窗间墙裂缝位置及趋势为一条剪切斜裂缝,而试验实测的窗间墙裂缝位置及趋势为2条交叉的斜裂缝,这是由于文中文献[16],对所有墙体均采取单调加载的方式来简化模拟其试验的低周往复加载所产生的差别,原因是考虑到进行低周往复荷载分析比单调荷载分析需要设定多得多的荷载步,复杂性也高出许多,因此采用方法可以简化计算过程,提高数值分析的效率,且从模拟对比来看,简化成单推方式并不会对其计算得出抗震承载能力造成较大偏差[16],其荷载-位移曲线与试验得到的骨架曲线吻合良好。故从以上分析来看,模型的裂缝分布情形符合实际情况,可用于接下来的参数分析。

图2 墙片ZQ1的破坏形态对比Fig. 2 Comparison of failure modes of wall ZQ1

图3 墙片ZQ3的破坏形态对比Fig. 3 Comparison of failure modes of wall ZQ3

由图4和图5可知,模拟和试验的荷载位移曲线都可简化为文献[17]的三折线模型,将荷载位移曲线表示为弹性、塑性、破坏3个阶段。开裂之前,荷载-位移曲线近似成直线,构件侧向刚度保持不变;开裂以后,刚度值下降,荷载-位移曲线斜率逐渐减小。设置了构造柱的墙片,构造柱对其形成约束,荷载达到极限荷载以后,相对于素墙片,其荷载位移曲线和坐标轴所包络的范围更大,其耗能能力更强。同试验相比,模型的荷载位移曲线和刚度退化曲线趋势基本与其吻合,验证了模拟时各参数设置的正确性。

图4 墙片荷载-位移曲线Fig. 4 Load-deformation curve of walls

图5 墙片刚度退化曲线Fig. 5 Stiffness degradation curve of walls

2 开洞纵墙拓展分析模型

为了得到墙片荷载-位移曲线的下降段,水平加载依然采用位移控制,位移的每一级增量为0.5 mm,加载时间间隔保持不变,加载点在墙片顶部。墙体各构件布置情况见图6。表5为各墙体模型信息。

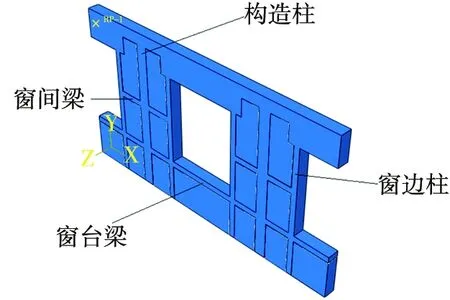
图6 墙片构件示意图Fig. 6 Schematic diagram of wall components

表5 墙片模型基本信息Table 5 Information of model walls

3 开洞纵墙的抗震性能分析

3.1 构造柱的影响

WA-1～8用于分析构造柱的影响,分析结果见表6, 图7为其中4种不同截面尺寸墙片模型的等效塑性云图。

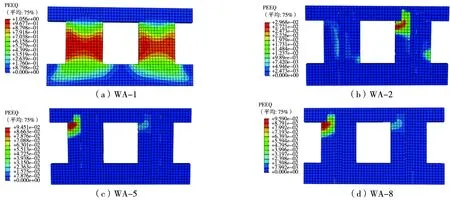
图7 等效塑性应变云图Fig. 7 Equivalent plastic strain nephogram

据表6可得,开洞墙片布置构造柱能够增强其承载能力,相对于素墙片WA-1,设置了构造柱的墙片WA-2～4峰值荷载比WA-1分别提升了10%、12.5%、14.9%。与此同时构造柱提升了墙体延性,设置了构造柱的WA-2、WA-3、WA-4位移延性系数分别比WA-1提高了约1.5、1.55、1.51倍。

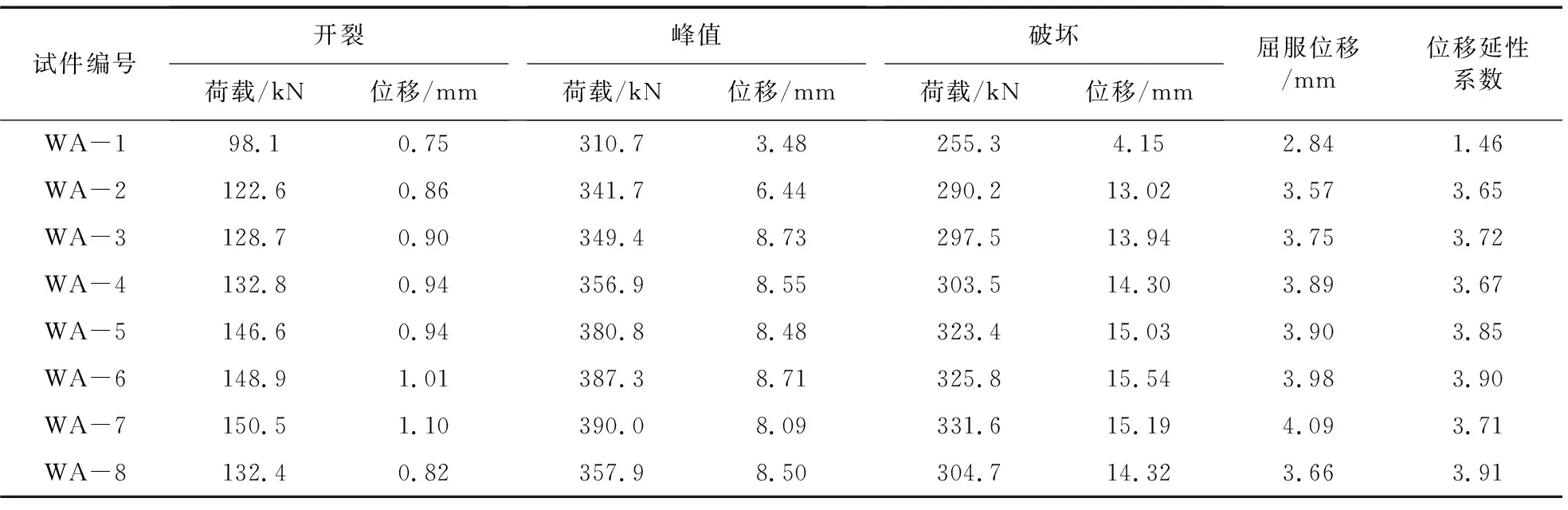
表6 不同构造柱墙片数值分析结果Table 6 Numerical analysis results of walls with different constructional columns

图8是WA-1和WA-2的荷载-位移曲线和刚度退化曲线,可以看到在后期构造柱对于墙体模型刚度影响很大,布置了构造柱的WA-2刚度降低较缓, 而WA-1因没有构造柱刚度快速的降低。从墙片发生开裂到荷载达到极限这一阶段,由于构造柱对墙片具有一定的约束作用,使得墙片即使开裂,但仍处于比较稳定的受力状态;墙片从承受极限荷载到被破坏这个过程中,构造柱对破碎的墙体产生有效的约束,使其仍可继续工作到构造柱不能继续承载为止。综上,墙片添加能够有效增强其承载性能,并增强其延性,延迟墙片开裂。

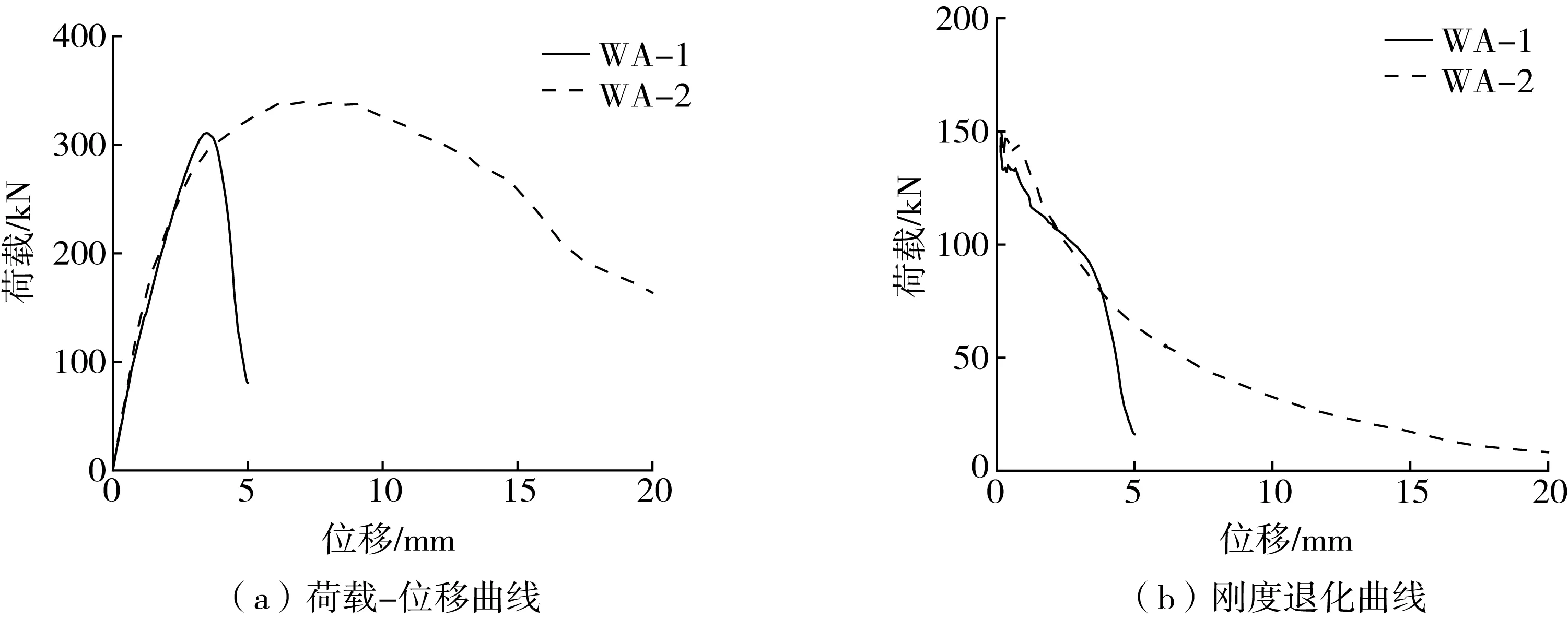
图8 墙片的荷载-位移曲线及刚度退化曲线Fig. 8 Load-deformation curve and stiffness degradation curve of walls

3.2 构造柱不同配筋率的影响

WA-2～4(240 mm×240 mm)与WA-5～7(370 mm×240 mm)用于分析构造柱配筋率的影响,得出其荷载-位移曲线(图9)及刚度退化曲线(图10)。

由图9、图10及表6,同WA-3比,WA-2的极限承载力降低了2.5%,WA-4的极限承载力提高了2.5%,而两者的位移延性系数都降低了1.5%左右。和WA-6比较,WA-5的极限承载力降低了1.7%,WA-7的极限承载力提高了0.7%,两者的位移延性系数分别降低约1.5%、5.3%。构造柱配筋率为1.4%的WA-3和WA-6发挥出了较好的变形能力、延性耗能能力。

图9 不同构造柱截面尺寸墙片在各配筋率下的荷载-位移曲线Fig. 9 Load-deformation curve of walls with different dimensions of structural columns in different reinforcement rates

图10 不同构造柱截面尺寸墙片在各配筋率下的刚度退化曲线Fig. 10 Stiffness degradation curve of walls with different dimensions of structural columns in different reinforcement rates

以上现象是因为构造柱中的纵筋能形成销栓作用,提升整个墙体承载性能的同时其耗能机制也会随之变化,在一定范围,销栓作用会随着构造柱配筋率增加而增强,构造柱与墙体的协调性变弱,这是造成以上墙片模型延性变差的原因。可得,墙片的承载能力会随着构造柱配筋率的增加而增加,但当构造柱配筋率超过某一范围时反而会对墙片延性的发挥造成不利影响。综上,墙体的中部构造柱有着界限配筋率,通过以上模拟分析得出,当其构造柱配筋率设置为1.4%时,墙体延性与承载性能最佳。

3.3 水平系梁与窗端柱的影响

WB-1～5用于分析水平系梁与窗端柱布置形式不同的影响,其数值分析结果见表7,图11为等效塑性应变云图。

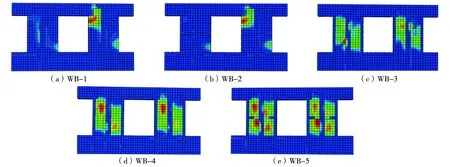
图11 等效塑性应变云图Fig. 11 Equivalent plastic strain nephogram

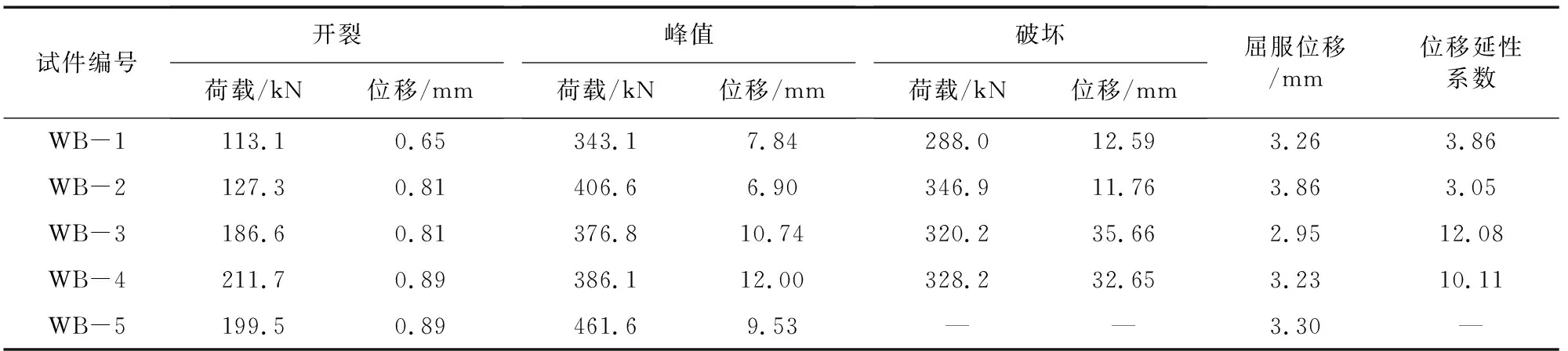
表7 不同布置形式的墙片数值分析结果Table 7 Numerical analysis results of walls with different layout forms

设有混凝土水平系梁的WB-1、WB-2与不设置混凝土水平系梁WA-2的荷载-位移曲线、刚度退化曲线对比如图12。

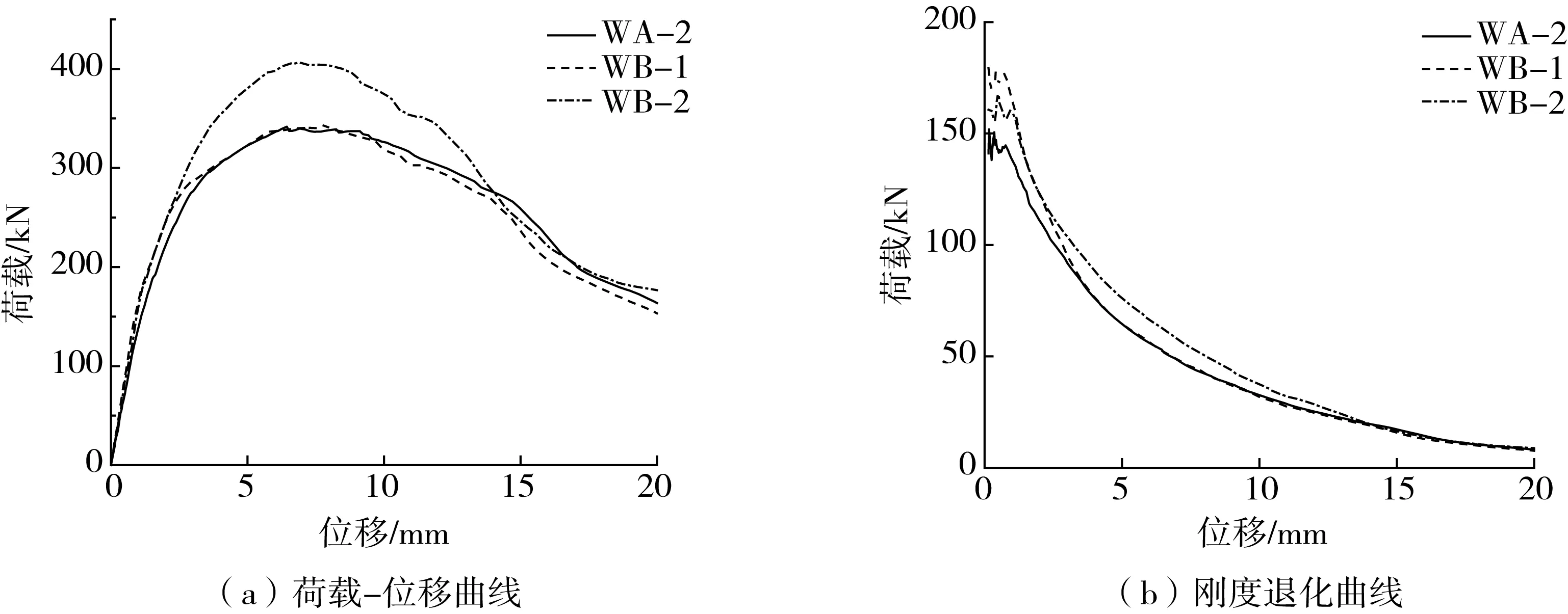
图12 有不同混凝土水平系梁墙片的荷载-位移曲线及刚度退化曲线Fig. 12 Load-deformation curve and stiffness degradation curve of walls with different concrete tie beams

由表6与表7可知,与WA-2比较,WB-1的开裂及破坏荷载低7.7%、0.8%,开裂与破坏位移低25%、3.3%,而峰值荷载、位移提升了0.4%、21.7%。可见于窗洞一半高度处的窗间墙内布置水平系梁,使得墙片位移延性系数提升了1.64倍,但是对抗侧刚度与承载性能的影响不大,原因在于系梁使中柱联结起来,降低了中柱的无支撑长度,由此墙体的变形能力得到加强。

墙片WB-2～5的荷载-位移曲线和刚度退化曲线图如图13所示,分析表7及图13可知:

图13 有不同构造措施墙片的荷载-位移曲线及刚度退化曲线Fig. 13 Load-deformation curve and stiffness degradation curve of walls with different structural measures

1)于开洞墙片的洞口一半高度处的窗间墙中布置一道联结构造柱的短钢筋混凝土水平系梁后,与WB-1比较,WB-2的承载能力提升18.5%,延性略有减弱,但荷载-位移曲线与坐标轴所围成的面积更大,这表明WB-2耗能能力增强,抗震性能有提升。

2)于洞口两边布置窗端柱后,相对于未布置的 WB-1,WB-3承载能力提高9.8%,位移延性系数提高2.13倍。这表明窗端柱的存在,优化了墙片的抗侧刚度与承载性能,延迟了裂缝的产生。

3)当窗端柱和水平系梁同时布置,墙体中纵横向的钢筋混凝土构架对其形成了有利约束,WB-4和WB-5的峰值荷载分别提升12.5%、34.5%,开裂荷载提升1倍,WB-4位移延性系数提高2.61倍,其破坏从脆性破坏变成延性破坏,抗倒塌能力得到很大提升。

综上,当洞口加设窗端柱与水平系梁,墙体的延性系数与破坏位移得到提升,优化了结构的抗剪承载力、变形能力、延性和耗能能力等抗震性能指标。故设置中部构造柱,同时在洞口处布置窗端柱与钢筋混凝土水平系梁是最佳的构造措施。

钢筋混凝土道路施工过程中，需要对钢筋结构进行加工，钢筋弯度制造时，应符合相应的设计需求，当设计规定不明确时，应满足下列要求：（1）半圆形钢筋制作时，半圆形钢筋的直径要超过钢筋直径的2.5倍，而弯钩预留的长度应大于钢筋直径的3倍；（2）直角钢筋制作时，钩端的长度应超过钢筋直径的3倍，直角弯钩的之间应超过钢筋直径的5倍。

3.4 开洞率的影响

建立窗洞大小为1 800 mm×1 800 mm的墙片WC-1、2,与墙片WA-1、2进行对比分析,其中WC-1没有构造柱,WC-2有构造柱,其数值分析结果见表8,图14为其等效塑性应变云图。

图14 等效塑性应变云图Fig. 14 Equivalent plastic strain nephogram

由表8可知,在不布置构造柱的情况下,与WA-1比,WC-1因开洞率更大而导致开裂、极限和破坏荷载分别降低52.6%、58.2%、56.6%,对应位移也降低了43.2%、54.8%、53.1%,但延性略有提升。在布置了构造柱的情况下,与WA-2比,WC-2因开洞率更大而导致开裂、极限和破坏荷载分别降低20.1%、33%、33%,对应的位移、延性几乎相同。这表明墙片因开洞率增大而明显降低了承载能力,且对无构造措施的墙片降低幅度更大一些,但对延性不会产生太大影响,可见一定的构造措施可以减小开洞率对墙片承载能力的影响。

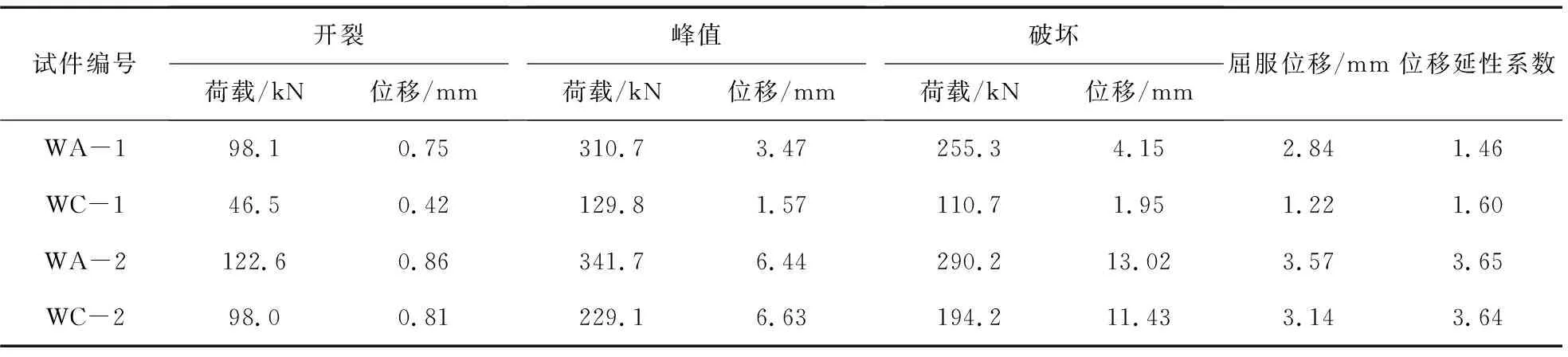
表8 不同开洞率的墙片数值分析结果Table 8 Numerical analysis results of walls with different opening rates

从图15中荷载-位移曲线和刚度退化曲线来看,随着开洞率增大,墙片刚度很明显的在下降,承载力也在降低,但延性只略有降低。同时,随着开洞率增大,荷载-位移曲线与坐标轴所围成的面积会减小,这表明耗能能力减弱,储备能力变差。开洞率会对墙体产生以上影响,原因在于洞口的四周会产生应力集中而形成薄弱区,这些地方会过早开裂,导致墙片的承载性能严重减弱,使其抗震性能变差,对砌体结构的抗震设计产生不利影响。综上,对砌体结构进行抗震设计时应着重注意开洞率较大的砌体墙部分,并在必要时采用加强构造措施等来提升其抗震性能。

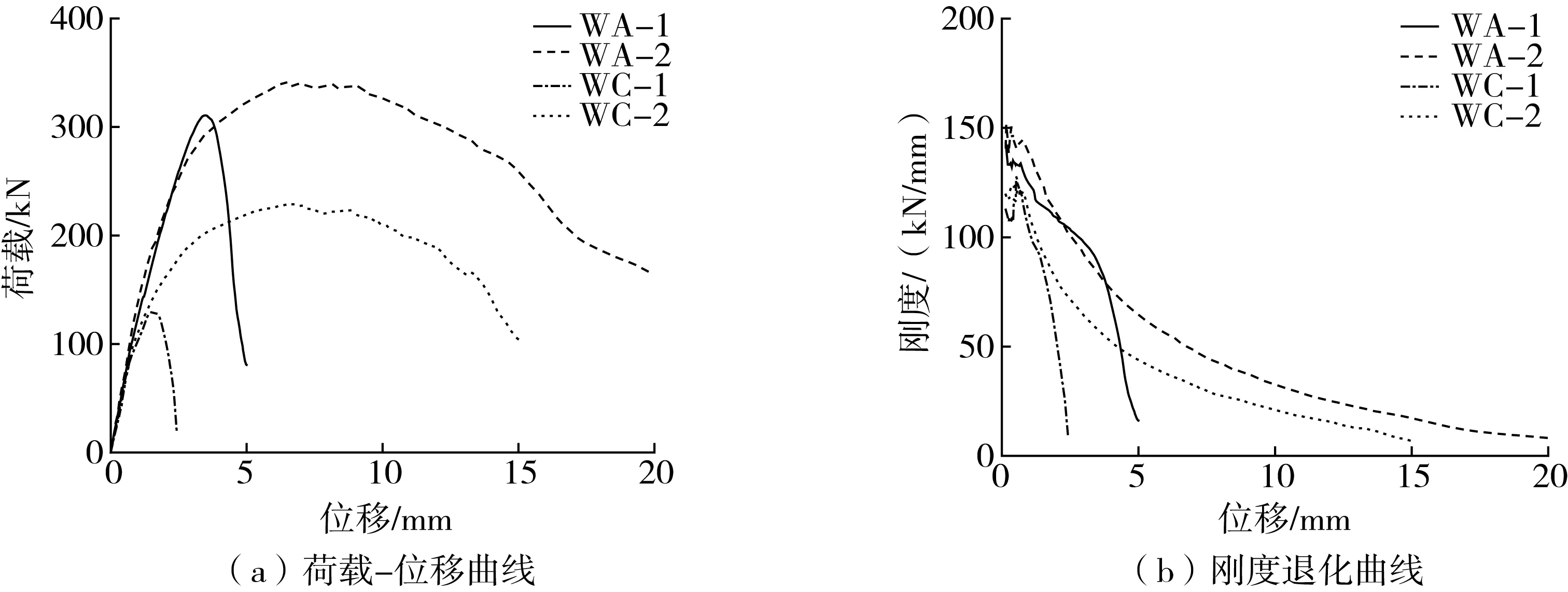
图15 不同开洞率墙片的荷载-位移曲线及刚度退化曲线Fig. 15 Load-deformation curve and stiffness degradation curve of walls in different opening ratio

3.5 开洞方式的影响

WD-1、2(开门洞)与开洞率相同的WA-1、2(开窗洞)用于分析开洞方式的影响,得到的数值分析结果见表9,在不布置构造柱的情况下,与开窗洞的WA-1相比,开门洞的WD-1的开裂、极限和破坏荷载分别提高约35.4%、19.3%、19.4%,对应位移也提高约5.4%、43.0%、74.7%,且位移延性系数增大71.6%。在布置了构造柱的情况下,相对于开窗洞的WA-2,开门洞的墙片WD-2的开裂、极限和破坏荷载分别提高约29.1%、8.2%、8.3%,对应位移也分别提高约4.5%、40.9%、14.1%,位移延性系数增大11%。综上,不同开洞方式对墙片的抗震性能影响较大,在相同开洞率下,开门洞墙片的承载能力相对于开窗洞墙片有明显提升,且位移延性系数也有一定程度的增大。

表9 不同开洞方式的墙片数值分析结果Table 9 Numerical analysis results of walls with different openings methods

图16为等效塑性应变云图,图17为墙片WA-1、2与WD-1、2的荷载-位移曲线和刚度退化曲线对比图。由图17可知,开门洞墙片的荷载-位移曲线与坐标轴所围成的面积比开窗洞墙片的大,墙片的承载力储备水平较高,耗能能力更强,延性更好,其抗侧刚度也相对开窗洞墙片高,配置构造柱墙片的刚度下降相对无构造柱墙片要慢,试件在加载过程中的损伤累积明显。故可得当开洞率相同,开门洞要比开窗洞更加安全。相比开窗洞,开门洞的墙片承载能力明显更高,裂缝会延迟出现,延性得到提升,有效避免了过早形成严重损坏。

图16 等效塑性应变云图Fig. 16 Equivalent plastic strain nephogram

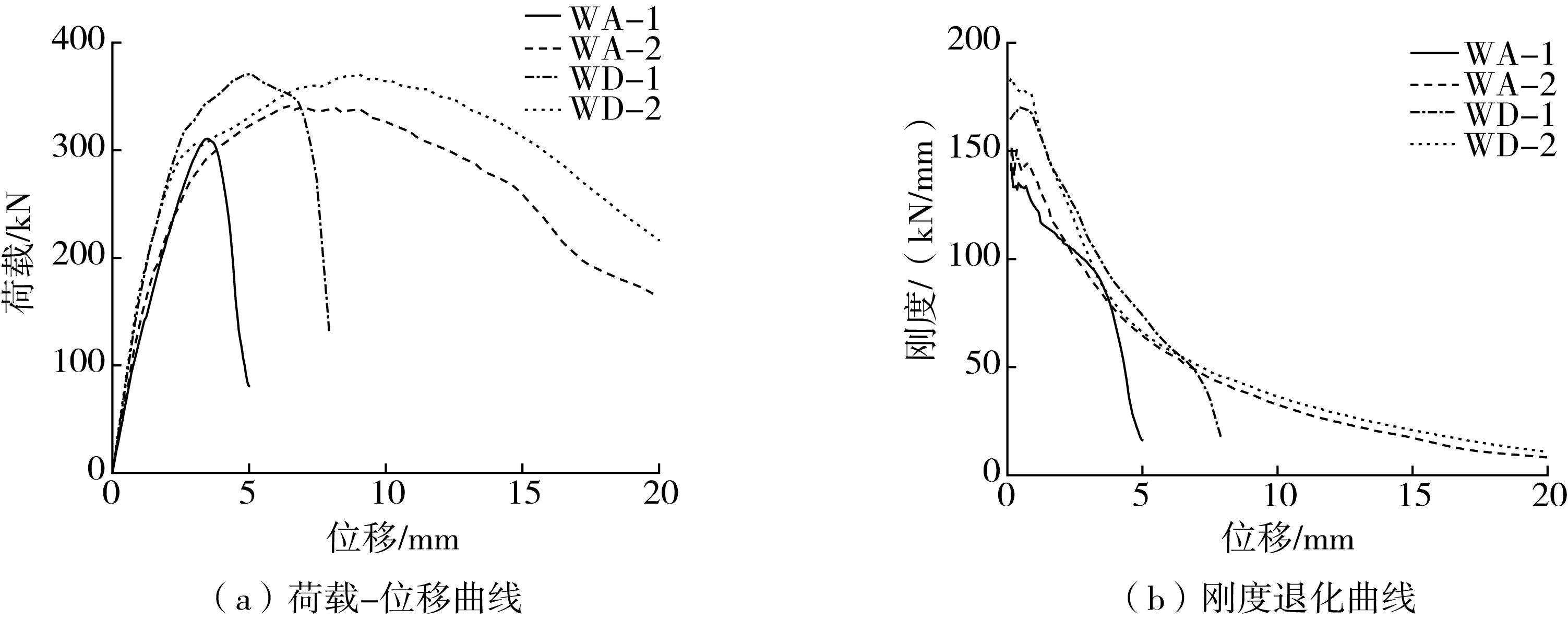
图17 不同开洞方式墙片的荷载-位移曲线及刚度退化曲线Fig. 17 Load-deformation curve and stiffness degradation curve of walls in different opening methods

4 讨论

对影响砌体墙抗震性能的主要因素进行了静力分析,考虑了构造柱、水平条带、窗端柱以及开洞率、开洞方式对开洞纵墙抗震性能的影响。相对于整体结构来说单片包含窗间墙的墙片是整个结构的子结构,但就所取模型墙片的承载力性能与破坏特征,特别是考虑各类构造措施对于其抗震性能的影响来说,从模拟分析结果来看依然是具有较好的吻合性,对于考虑各类构造措施、开洞率以及开洞方式的影响有着指导意义。

为了更好地反映实际情况,本节考虑纵墙的边界条件、地震传播的真实性等,以得出多层砌体结构不同构造措施下对应的适用烈度和高度建议为目的,根据文献[12]中的模型M2为模板建立了两层足尺砌体结构教学楼有限元模型,以调整地震波加速度值以及增加质量块的形式,对多层砌体结构的抗震性能进行分析,并将主要通过层间位移角评价不同构造措施在多层砌体结构中的应用情况。

各模型的尺寸、门洞及窗洞布置等均相同,钢筋混凝土扶壁柱截面为240 mm×370 mm,现浇楼板厚度100 mm,其余构件的基本参数如表10所示。本结构处于8度区二类场地,设计基本地震加速度取0.2 g;各层楼面做法按水磨石楼面考虑,恒载标准值取4.5 kN/m2;屋面为沥青蛭石,恒载标准值取5.1 kN/m2,楼面活载取2.0 kN/m2,屋面按不上人考虑,活载取0.5 kN/m2。模型中以等效密度的方法考虑结构荷载,一层钢筋混凝土板以5 500 kg/m3,二层以5 350 kg/m3计算。各不同构造措施的模型信息如表11所示,代表模型M4如图18所示。地震波选取地震分组为第一组、Ⅱ类场地土下的Imperial Valley波、El Mayor波和一条采用SeismoArtif软件中的Saragoni&Hart函数法生成的人工波,当中自然波的计算步长为0.005 s,人工波为0.01 s,持续时间为15 s。时程分析类型为直接积分,积分方法取用HHT方法。

表10 各构件基本参数Table 10 Basic parameters of each component基本信息构件名圈梁过梁角部构造柱中部构造柱截面尺寸(mm×mm)240×240240 ×370240×240240×500纵筋414616414414+316箍筋6@1506@1506@1506@150表11 模型信息表Table 11 Model information table模型名称构造柱位置混凝土水平系梁窗端柱层高/m设防烈度M1无无无3.3×28M2纵墙无无3.3×28M3纵墙有无3.3×28M4纵墙有有3.3×28M5纵墙有有3.3×29

计算得到模型在各地震波作用下各层(U)、纵墙(X)与横墙(Y)层间位移角均值如表12所示。模型M2、M3、M4比M1各层的层间位移角都要小,结构抗震能力明显更强,体现了构造措施加强的作用;与M2相比,设置了水平系梁的M3层间位移角数值差别不大,这表明水平系梁的添加对结构整体性能的影响较小。而相对于M3,设置了窗端柱的M4层间位移角影响比较大,故认为是窗端柱的加入,使得模型抗震能力明显增强。将结构横墙的最大层间位移角进行比较:M4>M3>M2>M1,这是因为构造措施增强以后,横墙的抗震性能降低,出现了纵横墙不协调的情况,仅对长度较长的横墙两端设置了构造柱,而横墙中部没有设置,导致中部墙区平面外变形没有得到有效约束,故实际工程中应于横墙中布置合理的构造柱。

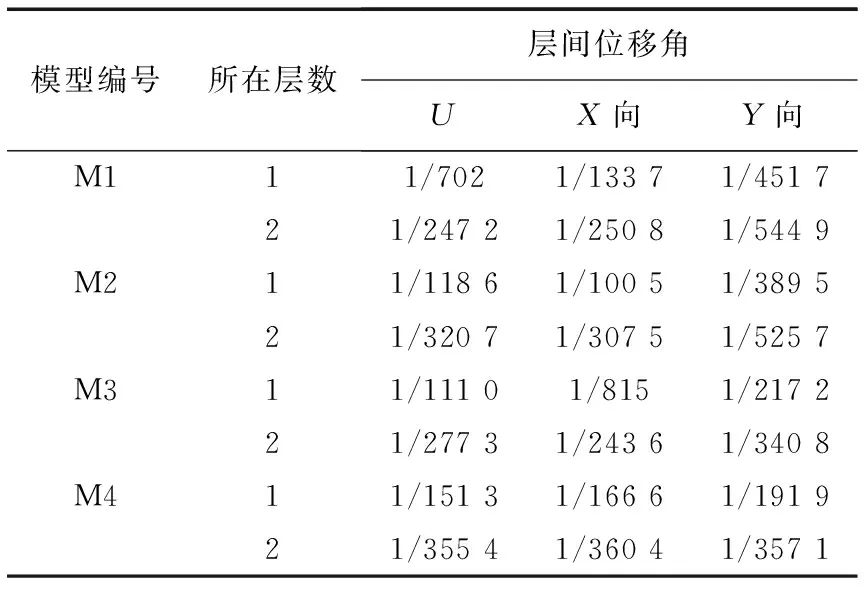
表12 各模型的层间位移角均值Table 12 Average value of interlayer displacement angle of each mode

计算得到模型在地震波作用下受拉损伤参数值(DAMAGET)如图19,其体现了模型中各单元塑性应变的大小,可以近似模拟结构的开裂程度,包括裂缝的大小和形状。可见窗洞处,特别是底层的窗间墙部分为墙体破坏主要集中处,相对于没有设置构造柱等构造措施的M1模型,M2与M3的底层损伤较小,破坏并没有那么显著。而M5(设置9度罕遇地震)由于是在更高强度地震作用下,其破坏损伤非常严重。结合图20来看,前文中所提取的包含窗间墙的模型墙片正是为该集中破坏区,是为后期可能造成纵墙严重损坏甚至垮塌的关键位置,对于整体结构纵墙部分的抗震能力及破坏形态具有代表性。

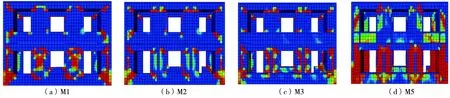
图19 整体模型在Imperial Valley波作用下的受拉损伤云图Fig. 19 Damaged nephogram of the overall model under the Imperial Valley wave

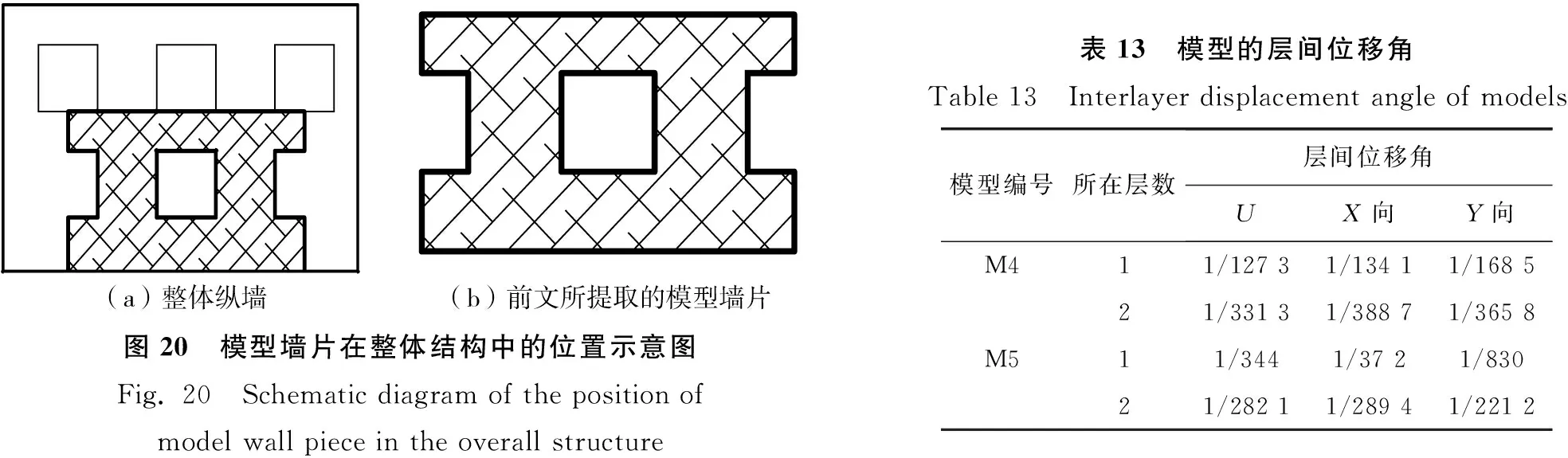
图20 模型墙片在整体结构中的位置示意图Fig. 20 Schematic diagram of the position of model wall piece in the overall structure表13 模型的层间位移角Table 13 Interlayer displacement angle of models模型编号所在层数层间位移角UX向Y向M411/127 31/134 11/168 521/331 31/388 71/365 8M511/3441/37 21/83021/282 11/289 41/221 2

4.1 高烈度下结构抗震性能讨论

为了探究当超过8度罕遇地震烈度的地震来临时高层砌体结构的抵抗能力,计算了模型M4遭遇9度罕遇地震波时的抗震性能(文中记为M5),表13为其层间位移角计算结果,可知随地震作用增强,各层层间位移角随之增大,结构损害更严重,M5的一层层间位移约为M4的4倍多,2层差距不大。但M5的最大层间位移角为1/344<1/250[18],说明模型仍在生命安全性能水平范围内而不会发生倒塌。综上,砌体结构在遇到超过罕遇地震烈度的巨震时,仍未失去水平承载能力,此时还保持一定的安全性。

4.2 不同高度下结构抗震性能讨论

前文是以模型层数为二层时进行的抗震性能分析,此时结构高度较低。因此下面继续研究结构在规范规定的层数内,将高度增加,构造措施进行调整的模型在面临8度、9度强地震时的抗震能力。在分析中考虑到纵横墙的匹配问题,所以在此将横墙均设置中部构造柱。

采用上文的2层模型作为子结构的思路,以增加配重(质量块)的方法来计算分析。因薄弱层一般位于结构底部,所以在此将重点放在最下面2层,而2层以上的重量以上述思路进行模拟(添加质量块),以砌体墙截面面积比进行分配。图21为多层模型M2-8-4与子结构模型图。表14为我国《建筑抗震设计规范》规定的多层砖砌体房屋层数和总高度限值。表15为计算结果。

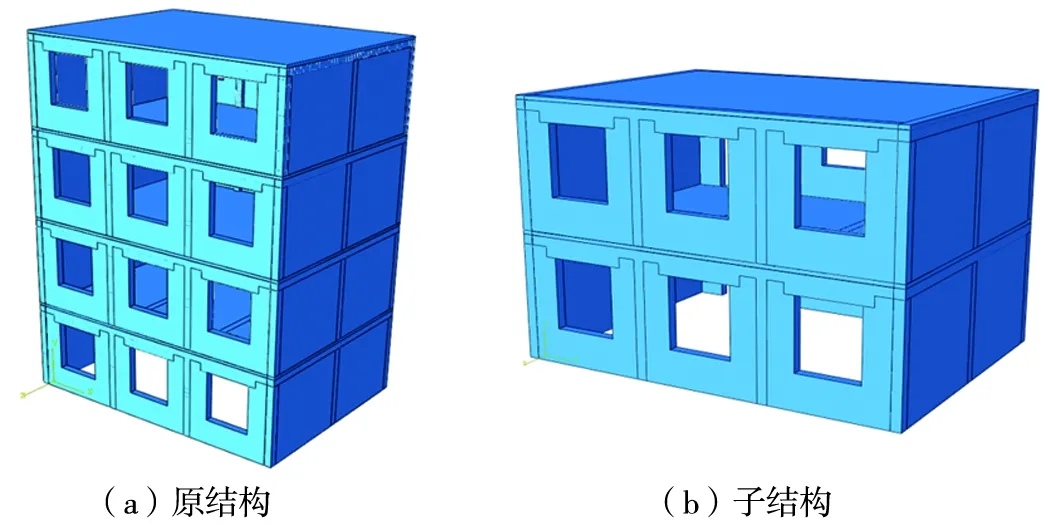
图21 模型M2-8-4Fig. 21 Model M2-8-4

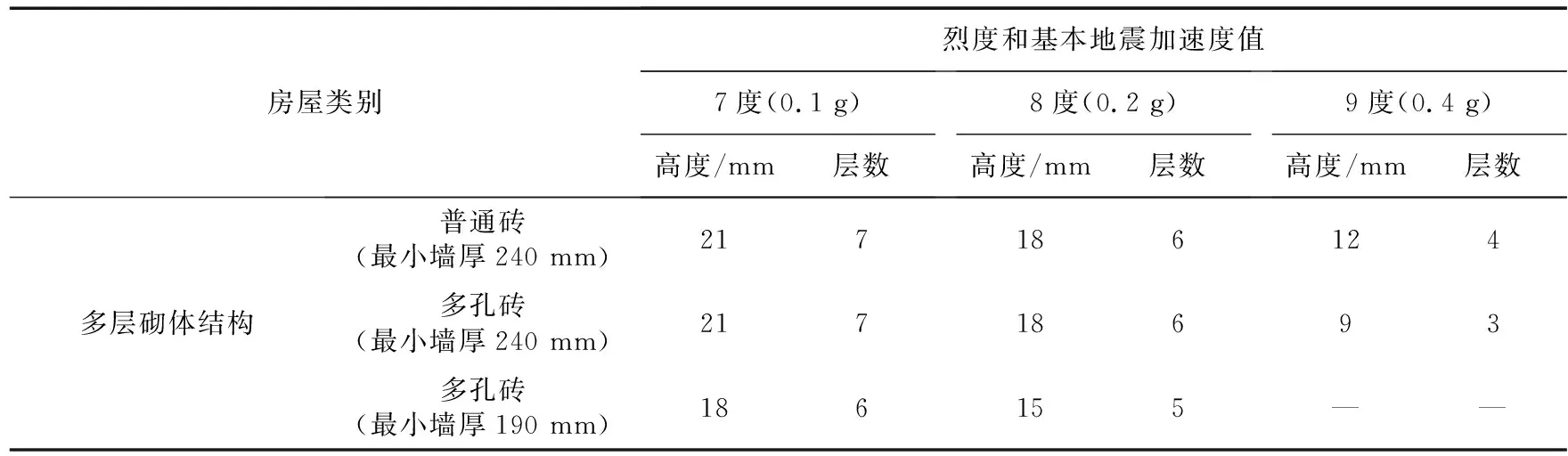
表14 房屋的高度和总层数限制值Table 14 House hight and the limit value of total layers

表15 各模型的层间位移角Table 15 Interlayer displacement angle of models

由表15可知,层间位移角随层数增高而增大;而构造措施的增强使得同条件下模型的抗侧刚度增加,层间位移角减小。因此,这2个因素是相互影响的,构造措施与层数的相互协调过程中,应能够分析讨论出较好的处理方式,为砌体结构房屋提供更好的抗震设计思想。

从计算结果来看,当模型设置第2类构造措施(布置构造柱,不布置水平系梁与窗端柱),设为5层时,其在8度地震作用下的最大层间位移角达到1/85,层数的增多导致结构底部所受的竖向压应力变大,地震过程产生较大变形,结构由整体破坏变成纵墙提前破坏,这时认定结构已经倒塌破坏。当其设为4层时,在9度地震作用下,与设置第3类构造措施(布置构造柱与水平系梁,不布置窗端柱)的模型相比,同条件下其层间位移角小,但其层数为3层与层数为2层的模型的层间位移角相差较大,且设为3层时,结构底部纵墙受压较大,并有弯曲。综上,当模型设置第2类构造措施时,在9度罕遇地震作用下可建造3层,但其高度应不超过规范规定值;在8度罕遇地震作用下只可建造4层。

当模型设置第3类构造措施(布置构造柱与水平系梁,不布置窗端柱),设为4层时,在9度地震作用下的层间位移角达到1/48,同上文所述,结构由整体破坏变成纵墙的提前破坏,这时认定结构已经倒塌破坏;当其设为5层时,在8度地震作用下,位移角减小,但和层数为4层时相差很大,且在4层时,底部纵墙已有小幅度的弯曲,所以认定结构为5层时也已倒塌破坏。综上,当模型设置第3类构造措施时,在9度罕遇地震作用下可建造3层,其高度可超出规范规定值;在8度罕遇地震作用下只能建造4层。

当模型设置第4类构造措施(布置构造柱、水平系梁与窗端柱),设为5层时,在8度地震作用下层间位移角为1/120,结构底部纵墙没有出现过大变形;设为6层时,模型底层纵墙发生很大的变形,这时认定结构已经倒塌破坏。在9度地震作用下,结构为3层时,层间位移角最大为1/131,结构底部纵墙受压比较大,有弯曲现象产生;当设为4层时层间位移角更大,并且整体破坏比较严重,故认定4层时也已倒塌破坏。综上,当模型设置第4类构造措施时,在9度罕遇地震作用下可建造3层,并且高度可以超过规范规定值;在8度罕遇地震作用下可建造5层,高度也可超出规范规定值。

5 结论

1)构造柱的布置较大程度地提升了窗间墙体的承载能力与延性,延缓了裂缝产生的时间,提升了耗能能力。另外,构造柱的配筋率对提高墙体性能也有一定的作用,柱截面尺寸一定时,随配筋率增大,墙体承载能力随之提升,但对墙体刚度的影响较小;但配筋率过大,墙体延性与耗能能力会下降,导致墙体抗震性能变弱;据上文模拟计算可知,墙体中部构造柱配筋率布置为1.4%为最佳配筋率。

2)在墙片已经布置构造柱的基础上继续加强构造措施,即于洞口一半高度处布置窗端柱与混凝土水平系梁,其承载能力也会随之增加,变形能力与延性得到提升,墙体抗震性能变好。故在墙体中部布置构造柱,且在其洞口一半高度处布置窗端柱与混凝土水平系梁是最好的构造措施。

3)开洞率与开洞方式也是两个重要因素。当墙体开洞率的增大,其承载力、刚度显著降低,抗震能力随之减弱;而开洞率一定时,不同的开洞方式与墙片抗震性能也有一定关联,开门洞显著提升了其承载力与延性,这时墙体不会过早的产生严重损坏,耗能能力得到提升,故开门洞相对于开窗洞是要更加安全的。所以对砌体抗震设计时应减少开洞率,以及合理设置门洞、窗洞。

4)当构造措施足够强时,砌体房屋能在历经超过8度罕遇地震烈度的大震后依然保持生命安全性能而不致发生倒塌,且未失去水平承载能力,保持一定的安全性。

5)设置中部构造柱、混凝土水平条带、窗端柱等构造措施可以增强砌体结构抗震性能,使得高烈度下的砌体房屋高度可适当超出规范规定,为高烈度下的多开洞纵墙砌体结构的抗震设计给出了相应的建议。因此,在保证安全的前提下,可以适当重新考虑规范中规定的高烈度下砌体房屋高度,充分利用建筑空间。