基于车辆响应的连续梁桥损伤识别数值分析

李祖栋,项长生,亓兴军,杨洪超

(1. 兰州理工大学 土木工程学院,甘肃 兰州 730050; 2. 山东建筑大学 交通工程学院,山东 济南 250101)

0 引言

YANG等[1]利用过桥车辆作为桥梁动力特性信息载体,基于车辆与桥梁的阻尼都为零以及桥梁只考虑一阶振型贡献的假设下,成功推导出车体响应的解析解,证明了车体加速度谱中包含桥梁的频率信息,并通过有限元模拟,验证了解析解与数值解的高度吻合。至此,桥梁间接测量法被正式提出,并逐渐应用于损伤识别。BU等[2]基于车辆动力响应相对于桥梁损伤指标的灵敏度分析,以车辆加速度为基础,采用正则化技术,成功实现了简支梁桥的损伤识别。NGUYEN等[3]基于运动车辆动力响应,通过小波变换的峰值位置和运动车辆速度识别了桥梁的裂缝位置。安宁等[4]利用车激桥梁响应互相关函数灵敏度方法,准确识别出了桥梁单元损伤位置。ZHANG等[5]提出全局滤波法(GFM),利用过往车辆的动态响应提取结构的工作挠度,并成功检测出梁类和板类结构的局部损伤。OBRIEN等利用车辆采集到的加速度信号,分别结合道路表观轮廓中的时移差[6]、基于模态振型平方的损伤指数[7]、基于经验模态分解(EMD)方法提取的对损伤敏感的速度伪频率成分[8]检测出了桥梁的损伤位置。贾宝玉龙[9]基于车辆响应,提取了桥梁一阶振动模态,结合改进的直接刚度法,通过节点刚度的变化,对桥梁的损伤程度和损伤位置进行了初步判定。HE等[10]利用运动车辆响应与希尔伯特变换结合,提取桥梁损伤状态下具有高空间分辨率的桥梁一阶模态振型,将损伤与未损伤状态下的区域模态振型曲率对比评价桥梁的局部损伤。ZHANG等[11]利用移动车辆的接触点响应,结合瞬时振幅平方(instantaneous amplitude square, IAS)对简支梁桥进行了裂缝损伤识别。YANG等[12]在ZHANG的基础上深入研究了不连续放大、环境噪声、车辆阻尼、桥梁阻尼等因素对IAS损伤检测能力的影响,证明IAS具有良好的鲁棒性。阳洋等[13]基于间接测量技术,利用识别的桥梁的一阶模态振型以及对应的桥频,结合改进的直接刚度法,成功识别了在粗糙度的影响下,桥梁的刚度损伤位置。阳洋等[14]利用固定间距的前后两辆测试车过桥采集到的信号,基于传递率的改进直接刚度法对桥梁单元刚度损伤进行了识别。

由于间接测量法的经济性和便捷性,此方法一经提出就受到了众多学者的研究和关注。然而,目前多数研究采用的计算模型都是普通的简支梁结构,并且车辆速度多为匀速,测试车型也较为单一。为充分探讨车桥振动间接测量法对多种超静定结构桥梁类型的适用性,扩大提升该方法未来应用于实际桥梁工程的潜在应用范围,文中以一实际工程中的两跨连续梁桥为例,借助IAS方法,在研究了匀速状况下不同速度对裂缝损伤识别精度影响的基础上,对匀加速以及匀减速行驶的车辆采集的加速度信号能否准确识别连续梁桥的损伤也进行了分析。双轴车行驶过程中由于前后质量以及悬架刚度的不同,车体质量点不仅会竖向振动还会发生转动,为明确这种更接近实际的双轴车采集到的竖向加速度信号能否像单轴车一样定位损伤,车体的转动是否会影响损伤识别的精度,文中对双轴车得到的损伤结果进行了充分细致的分析。此外,还讨论了路面粗糙度、车辆阻尼比等因素对损伤识别的影响,进一步完善了IAS方法在连续梁桥损伤识别数值分析中的适用性和有效性。

1 理论基础

车辆竖向加速度公式求解参照文献[15],单轴车以匀速v通过一座长度为L的简支梁桥,移动车辆简化为簧上质量块,车体集中质量为mv,车辆刚度为kv。桥梁视为欧拉-伯努利梁,桥面光滑,桥梁为等截面,质量分布均匀。桥梁的单位长度质量为m、材料的弹性模量为E、截面惯性矩为I,车辆过桥简图如图1所示。

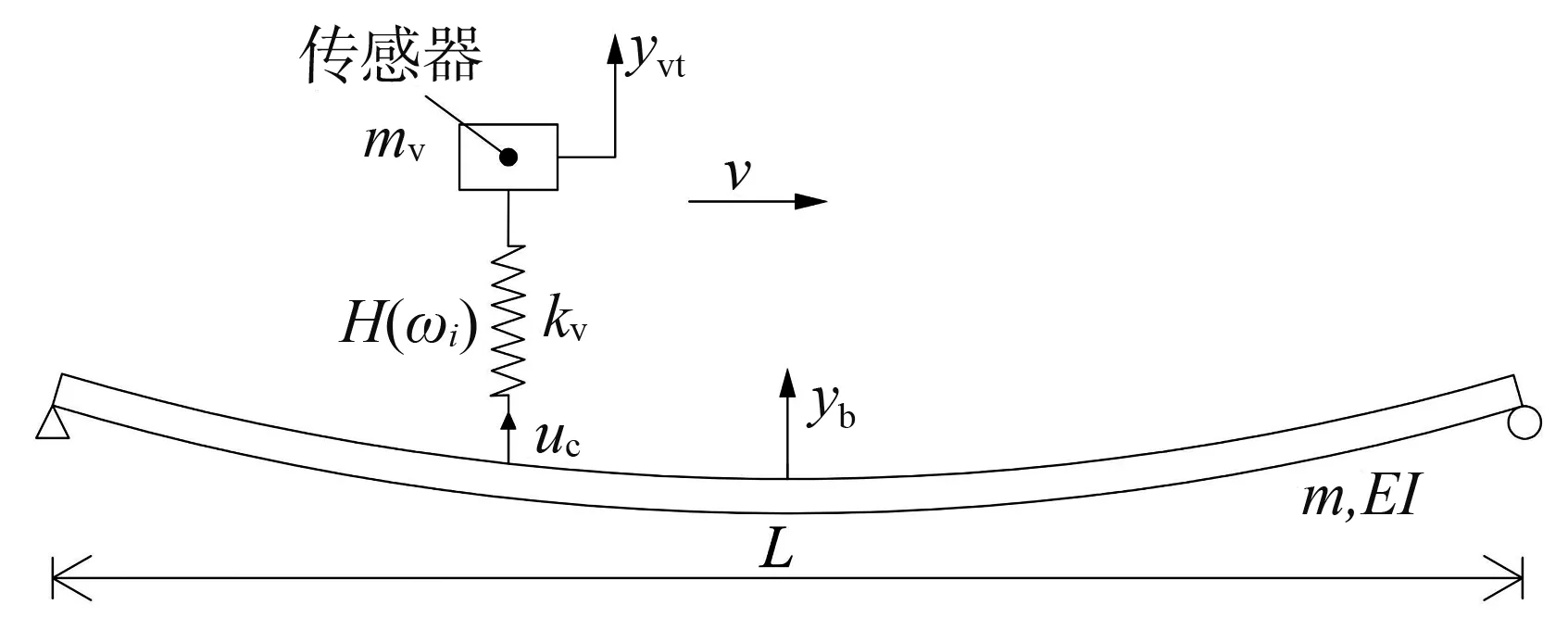
图1 单自由度车辆驶过桥梁简图 图2 裂缝模型示意图

不考虑车辆与桥梁的阻尼,分别得到车体与桥梁的动力方程,如式(1)、式(2)所示:

mvv+kv(yv-uc)=0

(1)

mü+EIu′′′′=[kv(yv-uc)-mvg]δ(x-vt)

(2)

式中:yv为车体的垂直位移;uc为运动车辆与梁接触点的位移;δ为狄拉克函数。

经推导得到车体的竖向加速度为:

(3)

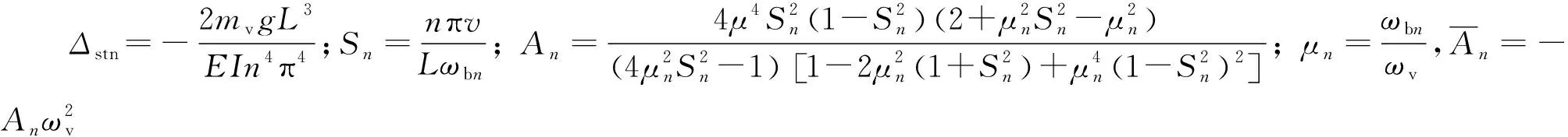
车体加速度驱车分量响应分析由文献[16]可知,

(4)

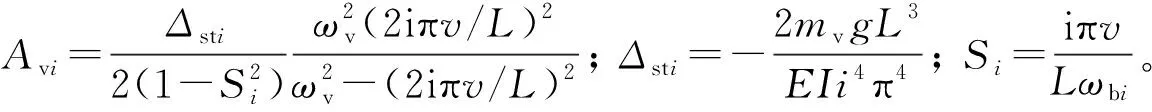
对式(4)做希尔伯特变换,得:

(5)

结合式(4)、式(5),求得驱车分量响应随时间变化的瞬时振幅平方(IAS)如式(6)所示:

(6)

由于车辆匀速运行,在桥上的位置x=vt,简支梁桥的第n阶模态函数φn(x)=sin(nπx/L),因此式(6)改写成:

(7)

由式(4)可知,驱车分量Rvd(t)包含了桥梁的密集信息,而驱车分量的IAS主要受振型φn(x)的影响[11],振型在损伤处会产生突变[17],因此这种特性可以检测梁的损坏。此外,IAS中涉及的平方运算具有使大的量变大,小的量变小的理想特性,从而更容易识别梁的损伤[12]。

基于上述的理论,数值模拟进行损伤识别的流程如下:1)在量测车上安装传感器,采集传感器收集到的车体的竖向加速度信号;2)对加速度信号进行快速傅里叶变换,使用带通滤波将驱车频率对应的信号分离出来,之后将其逆傅里叶变换,还原成时域信号;3)对分离出来的驱车频率分量响应进行希尔伯特变换,并对结果取平方;4)通过IAS识别结果图中的峰值位置来判断桥梁的损伤位置。

2 模型参数

根据车桥耦合振动分离法原理,基于ANSYS瞬态动力学求解功能,采用APDL语言实现车辆过桥的耦合动力时程响应分析[18]。

2.1 损伤模拟

考虑到运营中的桥梁容易出现裂缝损伤,因此通过ANSYS在相邻单元之间的2个节点上加入1个长度为0的铰链,此铰链用combin7单元模拟,裂缝模型示意图如图2所示。对于矩形梁,裂缝的等效转动刚度k可以估计为[19]:

(8)

2.2 桥梁建模

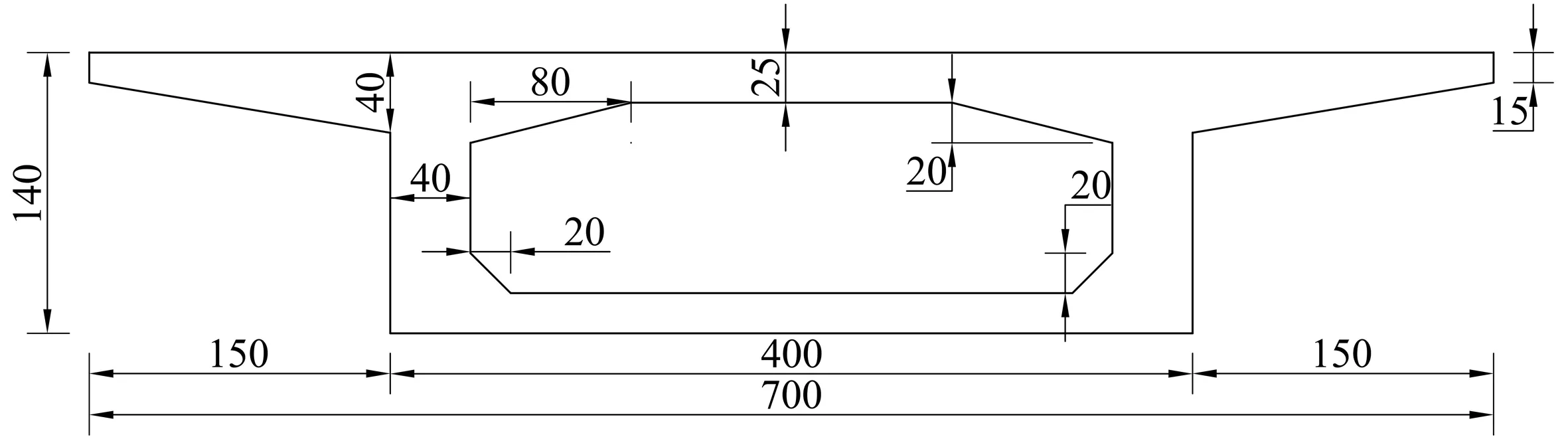
图3 连续梁桥横截面图Fig. 3 Cross-sectional view of continuous beam bridge

2.3 车辆建模

车辆模型示意图如图4、图5所示。

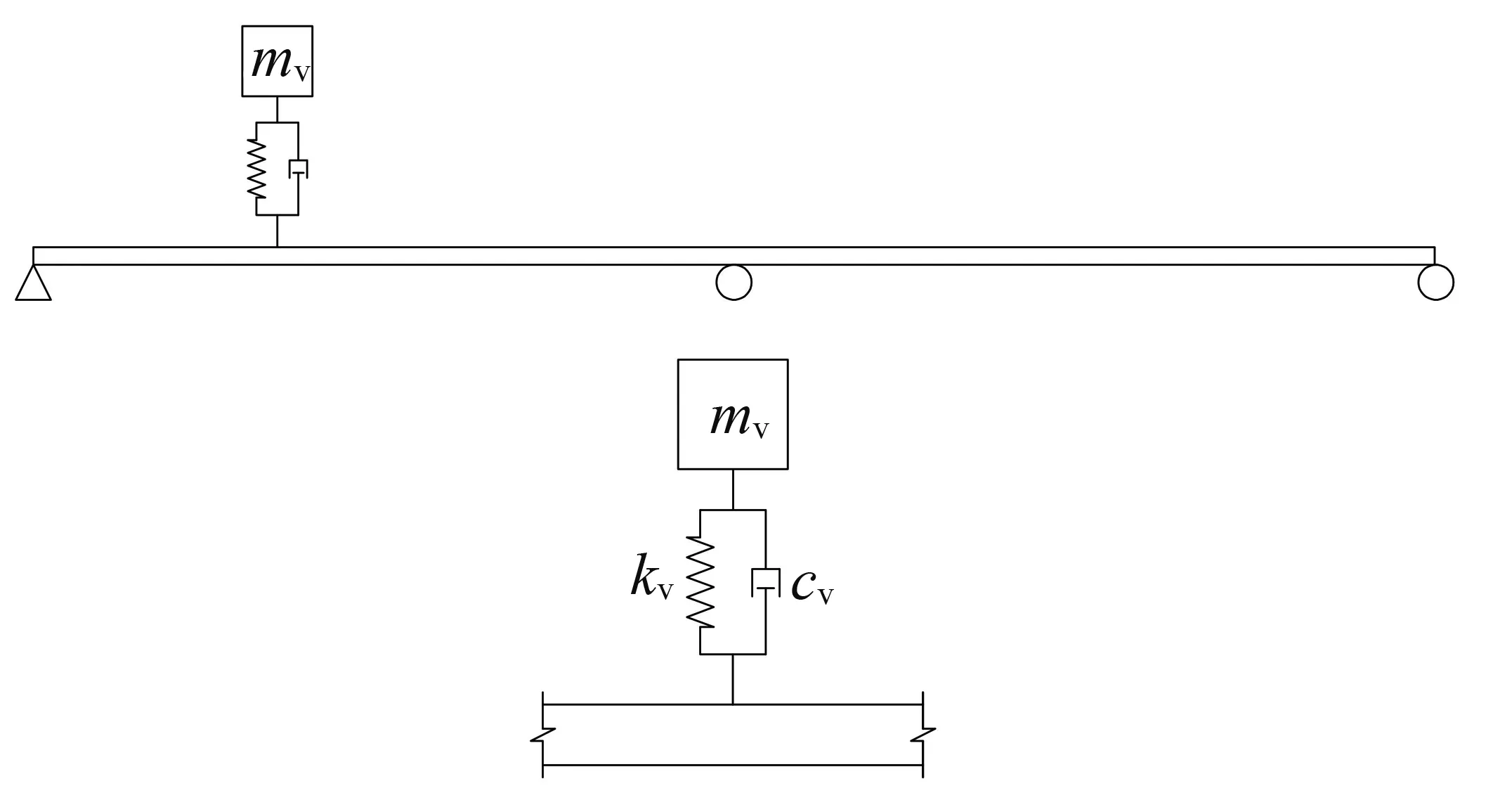
图4 单轴车过桥示意图 图5 双轴车过桥示意图

车辆模型[20]的具体参数如下:

单轴车:质量mv=1 000 kg,刚度kv=170 kN/m,阻尼系数cv=2 607.68 N·s/m,阻尼比为10%。

双轴车:质量M=1 000 kg,转动刚度Iv=400 m4,前后悬架的刚度分别为k1=50 kN/m,k2=37.5 kN/m,阻尼系数c1=654.79 N·s/m,c2=1 216.04 N·s/m,阻尼比为10%,质心离前后轮的水平距离分别为d1=1.33 m,d2=0.67 m。

单轴车的竖向振动频率计算公式如式(9):

(9)

相比于单轴车,双轴车不仅有竖向振动频率,还包括转动频率,计算公式如式(10)[20]:

(10)

式中,Iv为车体点头刚度。

经计算,单轴车的竖向振动频率ωv为2.08 Hz,双轴车的竖向振动频率ωv为1.49 Hz,转动频率ωθ为2.35 Hz。

3 不同条件下桥梁损伤识别效果

为更好地提取驱车响应,带通滤波范围应该尽可能包括更多的驱车频率[12],滤波过程会受到车体频率和一阶桥频包含的能量向滤波范围泄露的影响[16],因此选择合适的滤波范围至关重要。

图6为单轴车以1 m/s的速度过桥采集到的信号经快速傅里叶变换得到的频谱图,从图上可以看到A点为一阶驱车频率,B点为车辆的竖向振动频率,C点为桥梁的一阶频率,D点为桥梁的二阶频率[21-22]。由于高阶驱车频率的能量非常小,无法识别获得,且一阶驱车频率的数值也很小。因此当车速为1 m/s时,可以将滤波范围选取为0～1 Hz,此范围内包含多阶驱车频率。下文中如果没有特别说明,车速以及滤波范围保持不变。

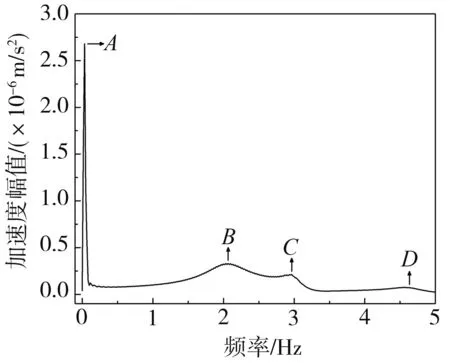
图6 车辆加速度频谱图 图7 IAS识别图(不同损伤程度)

3.1 损伤工况对损伤识别的影响

3.1.1 不同损伤程度工况

将桥梁的裂缝损伤程度分别设置为5%、10%、20%,得到不同损伤程度下IAS识别结果,如图7所示。图中竖向红色虚线是连续梁桥的两处损伤位置。当损伤程度为5%时,峰值点较小,可以勉强识别桥梁的损伤位置。随着损伤程度的增大,IAS识别图中的峰值也随之增大;当损伤程度为10%和20%时,能够快速准确地识别出损伤位置。由图7可以发现,两跨连续梁桥两端附近的IAS识别图有突起,这是因为两端附近的边界效应引起的强烈振荡会削弱结果的分辨率[11]。此外,30 m处对应的IAS识别图中由于该处存在支点也会稍微突起,当桥梁裂缝的损伤程度为5%、10%时,在判断损伤位置时,会受到中支点处IAS值的干扰,中支点处突起的原因是当量测车经过中支点上方的梁时,由于中支点的约束,梁的振动减弱,车辆采集到的信号包含的桥梁高阶模态数量减少,这等同于振型在中支点处产生了突变,由理论基础中式(7)知IAS方法主要受振型的影响,因此IAS识别图在中支点处会产生峰值点。在之后的数值模拟中,人为忽略中支点处的突起,即可对桥梁的损伤位置精准定位。

3.1.2 多裂缝损伤工况

实际工程中,服役期限较长的桥梁经常会存在多条裂缝。以文中的2跨连续梁桥为例,由于我国交通量大,车辆超载现象时有发生,2跨的跨中附近弯矩较大,当车辆荷载作用下桥梁的响应值超过设计挠度时,桥梁跨中位置处可能会出现损伤。为研究IAS方法识别连续梁桥跨中位置处多裂缝损伤的效果,在桥梁的第1跨10、15、20 m处,以及桥梁的第2跨44、45、46 m处均设置损伤程度为20%损伤。经计算,桥梁的前3阶频率分别为2.94、4.67、12.12 Hz。此外,由于支点负弯矩的存在,支点位置处也可能会有裂缝。为进一步研究IAS方法在实际桥梁裂缝病害中的适用性,在中支点及其附近位置29、30、31 m处,以及2跨的跨中位置15、45 m处均设置损伤程度为20%的损伤,此时桥梁的前3阶频率分别为3.03,4.57,12.30 Hz,由此可见桥梁的多裂缝对于桥梁的频率影响是很小的,因此滤波范围保持0～1 Hz不变。IAS识别结果如图8所示,图8(a)表明IAS方法可以较为准确地识别出桥梁2跨跨中及其附近位置处的6处损伤,对于第2跨较近的3处损伤,3个峰值互不干扰;图8(b)表明IAS方法无法识别中支点及其附近1 m范围内的损伤,这也是IAS方法的缺陷。

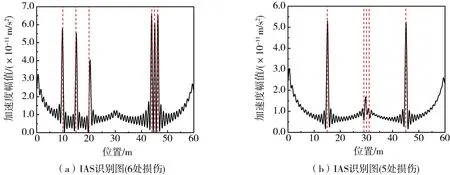
图8 不同损伤位置处下IAS识别图Fig. 8 IAS identification diagram at different damage locations

3.2 车速对损伤识别的影响

3.2.1 匀速

在匀速状况下,车辆以1、2、4、6 m/s的速度分别通过2跨连续梁桥,得到的IAS损伤识别的结果如图9所示。由图可知,随着车速的增加,IAS识别结果图中的加速度幅值随之增大,损伤识别的精度却逐渐下降。当车速为1 m/s时损伤的识别效果最好,这是因为车速较低时,车辆传感器驶过桥梁时可以采集到更多的振动信号。当车速增加时,增大了对桥梁的激励,由于车-桥相互作用,因此车辆的加速度也会随之增大。车速增加也会使第一阶驱车频率增大,而滤波的范围保持在0～1 Hz之间未变,此范围内包含的高阶驱车频率减少,因此识别精度降低。

由图9(a)～(d)可知,随着车速的增加,损伤处的IAS识别值与中支点(30 m)处的IAS识别值的比值逐渐减小,这是因为车速的增加对式(7)IAS结果的贡献小于量测车经过中支点时,受中支点约束的影响,车辆采集的信号包含的桥梁高阶模态信号减少对IAS结果的贡献。当车速为4、6 m/s时,中支点(30 m)处的峰值与损伤位置处的峰值基本相同,这对损伤点的定位造成了干扰。未来IAS方法用于实际桥梁损伤检测时,为减小中支点对损伤识别结果的干扰,应尽量采用1 m/s的速度行驶;如果对车速有较高要求时,根据数值模拟的结果,要人为忽略中支点处的突起,即可定位损伤。前文研究表明IAS方法的缺陷是无法识别中支点处的损伤,在实际工程中对于中支点处的损伤要结合其他方式进行辅助定位。当车速为6 m/s时,仍可以识别出损伤的位置,识别精度可满足工程需求。

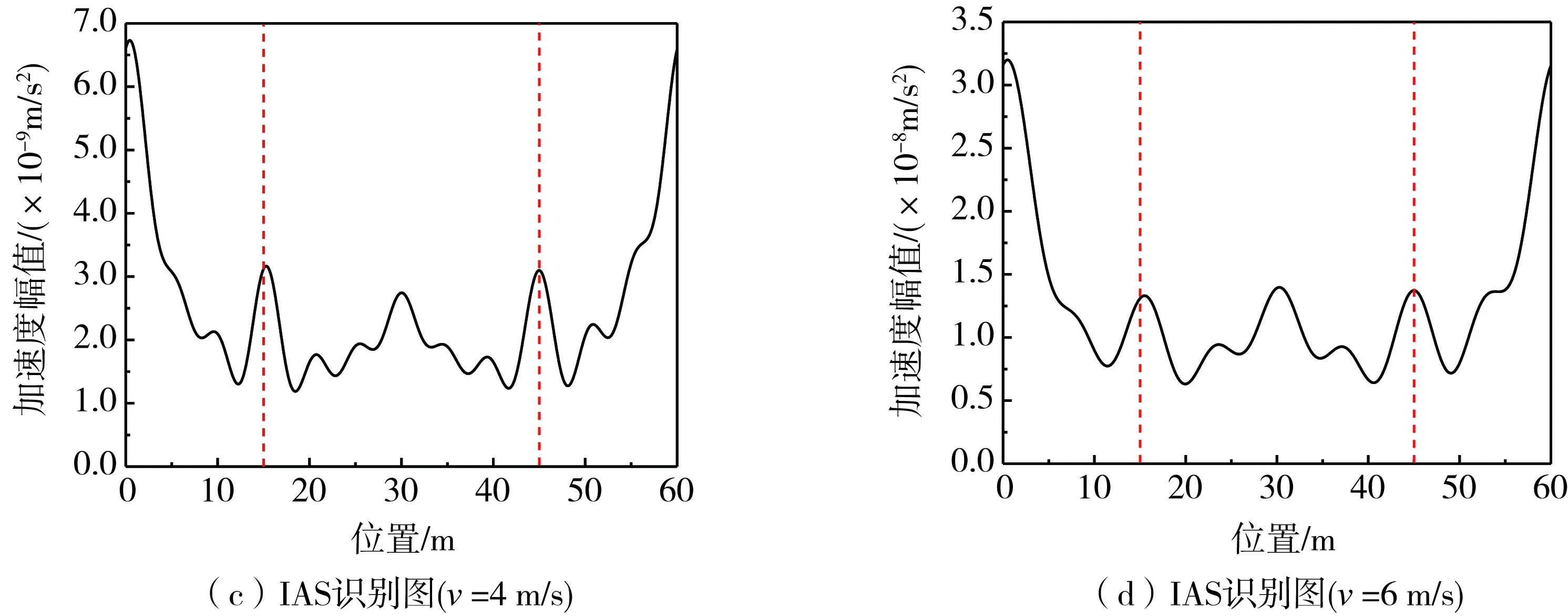
图9 不同车速下IAS识别图Fig. 9 IAS identification diagram at different vehicle speeds

3.2.2 匀变速

变速状况下,车辆以2.5 m/s的初速度上桥,加速度为0.4 m/s2,匀加速行驶6 s,6 s后车辆加速到4.9 m/s,此时以4.9 m/s的速度匀速行驶4 s,最后以加速度为-0.6 m/s2匀减速行驶,直至下桥。车辆沿纵桥向行驶的动态位移时程曲线如图10所示。从图中可以看出,当车辆经过第1个损伤点时,车辆处在匀加速阶段;当车辆经过第2个损伤点时,车辆处在匀减速阶段。通过变速车辆采集到的加速度信号得到的IAS识别结果如图11所示,从图中可以看出,两处损伤位置都产生了较大的峰值点,损伤识别结果与理论值基本吻合,表明了在车速合适的范围内,匀变速行驶的车辆仍然可以准确地定位损伤。将图11与图9进行对比,得出图9中的IAS识别结果图中的15 m与45 m这两处损伤位置处的峰值是相同的,而图11中的45 m处的峰值大于15 m处的峰值。经计算,车辆经过第1个损伤点(15 m)时,车速为4.27 m/s,经过第2个损伤点(45 m)时,车速为4.49 m/s,由此也可以看出车速增大时,IAS损伤识别图中的峰值点也会增大。

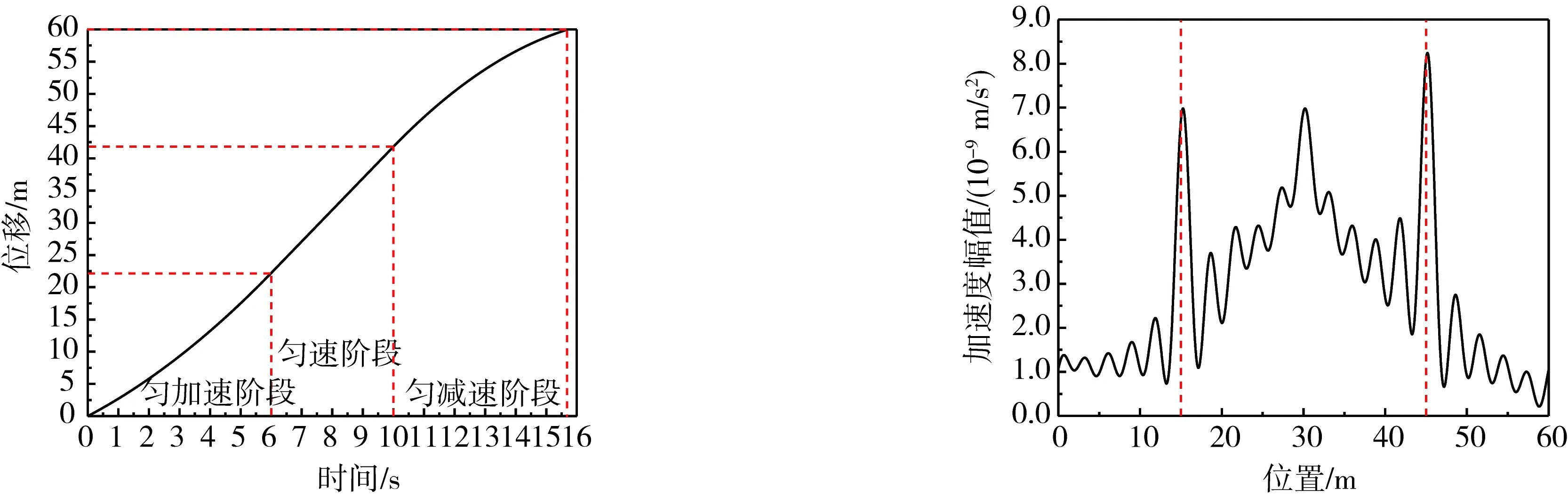
图10 车辆纵向位移动态图 图11 IAS识别图(变速)

3.3 粗糙度对损伤识别的影响

路面粗糙度在实际应用中是无法避免的,且对车辆振动响应的影响较大[23]。根据ISO8608[24]模拟A级、B级路面粗糙度,如图12所示。加入A级粗糙度后,使用1 t的量测车无法识别出损伤的位置,因为粗糙度的加入对车辆传感器采集到的加速度信号有较大干扰,在一定程度上掩盖了驱车频率。为减小粗糙度对桥梁响应的影响,通过增加量测车的车重来增加对桥梁的激励。量测车的车重分别设为1、5、10、15 t,车辆频率可能由于泄露而对滤波过程产生影响,因此要使车辆的频率尽量远离滤波范围,将车辆的刚度分别设置为170、800、1 600、2 400 kN/m,车辆的阻尼比均设置为10%。此时车辆的频率分别为2.08、2.01、2.01、2.01 Hz。损伤识别图如图13所示。由图13可以看出当量测车车重增加到10 t时,已经基本能识别出桥梁的损伤位置,当车重为15 t时,识别精度是很好的;而当车重为1、5 t时,由粗糙度对损伤识别造成的干扰无法消除。加入B级路面粗糙度后得到的IAS识别结果如图14所示,由图14可以看出当路面粗糙度增大到B级时,采用增加量测车车重的方式无法识别出桥梁的损伤位置,采集到的路面不平度信号完全覆盖了驱车频率信号,IAS识别图中反应的都是B级路面粗糙度的信息。

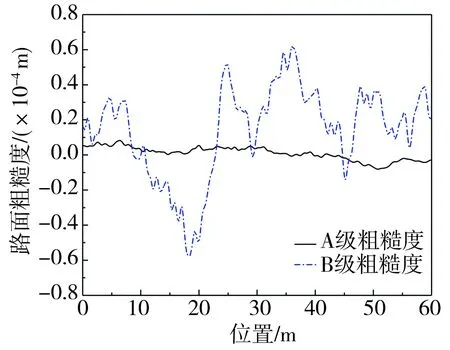
图12 路面粗糙度Fig. 12 Road surface roughness

图13 IAS识别图(A级路面粗糙度) 图14 IAS识别图(B级路面粗糙度)

3.4 单轴车与双轴车损伤识别结果对比

相比于单轴车,双轴车采集到的信号更加丰富。由于双轴车的竖向振动频率为1.49 Hz,为减少车体频率能量泄露对滤波造成影响,因此适当减小滤波范围,此部分滤波范围为0～0.8 Hz。在车辆行驶的过程中,双轴车车体质量点不仅竖向振动,而且由于车辆前后轴的刚度不同,前后重量不对称,车辆会发生俯仰,此时车体质量点还会存在转动加速度。

双轴车过桥简图如图15所示。车辆从位置1开始以1 m/s的速度匀速行驶到位置8结束。传感器安装在车体质量点处,将传感器开始采集信号的点定为坐标原点,因此传感器采集到的加速度信号对应的坐标区间是[0,62]。当车辆行驶到位置2时,传感器在2 m处,车后轴上桥,此时由于车桥响应系统参数突变[11],图16中的IAS识别结果图中A点会产生一个峰值。车辆继续前行到位置3时,此时双轴车的前轴到达了损伤处1,裂缝损伤会使加速度传感器采集到的信号发生突变,而此时传感器在15 m处,因此在此处会定位为损伤位置。车辆前行到位置4时,传感器在17 m处,由于双轴车后轴经过了损伤处1,所以在17 m处也会定位损伤的位置。同理,当车辆前行到位置5、6时,也会识别出损伤。车辆行驶到位置7时,前轴下桥,此时60 m处,对应的IAS识别图中的F点会产生峰值。因此,从理论上看,车辆传感器识别到的损伤位置分别为2、15、17、45、47、60 m,对应图16中竖向红色虚线的位置。通过双轴车采集到的竖向加速度信号识别出的损伤的位置分别为2.16、15.18、17.06、45.08、46.98、60.00 m。如果忽略识别误差,图16中B点与C点的距离,D点与E点的距离和双轴车的长度相同。此外,从图16可以看出,C点与E点的峰值均大于B点与D点的峰值,这是因为车体质量点距离车辆后轴较前轴更近,车体质量点处的传感器采集到从后轴传递来的损伤信号更强烈,因此C点与E点的峰值更高。

图15 双轴车过桥简图Fig. 15 Diagram of a two-axle vehicle crossing the bridge

车辆在采集竖向加速度信号的同时,也会采集到转动加速度信息,两者相互耦合[20],因此从理论上说,通过转动加速度也可以识别出桥梁的损伤,识别结果如图17所示。识别到的损伤位置分别为2.06、15.16、16.98、45.12、46.94、60.20 m,图中峰值点的产生原因与图16完全相同。综上所述,通过双轴车车体采集到的竖向加速度信号与转动加速度信号进行损伤识别,能够较为准确地识别出损伤的位置,识别效果与单轴车效果相同。但是由于双轴车相比于单轴车增加了一个转动频率,如果不对车体频率进行限制,可能会压缩滤波范围,造成识别精度下降,因此在数值模拟中采用单轴车更容易分析问题。

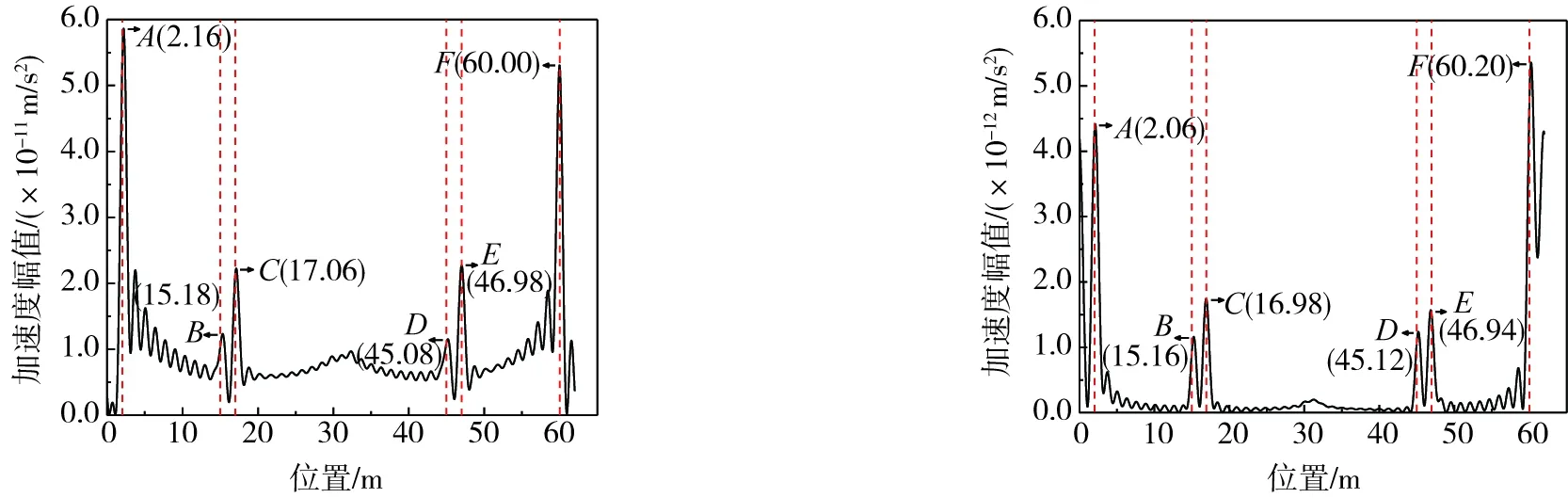
图16 IAS识别图(竖向加速度) 图17 IAS识别图(转动加速度)

3.5 车辆阻尼比对损伤识别的影响

在公式推导的过程中,忽略车辆阻尼的影响,而在实际测试现场中,车辆阻尼是必然存在的。将单轴车与双轴车的阻尼比均设置为0%、10%、20%进行损伤识别,得到不同车辆阻尼下单轴车的IAS识别结果如图18所示,双轴车的IAS识别结果如图19所示。由图18、图19可以看出车辆阻尼的变化不会对损伤识别的结果产生影响,这是因为车辆阻尼主要影响车辆响应的高频分量而不会影响用于计算IAS的驱车频率分量[12]。此外,由式(4)也可以看出,车体加速度驱车分量响应只和车速、梁长有关,与车辆阻尼无关。

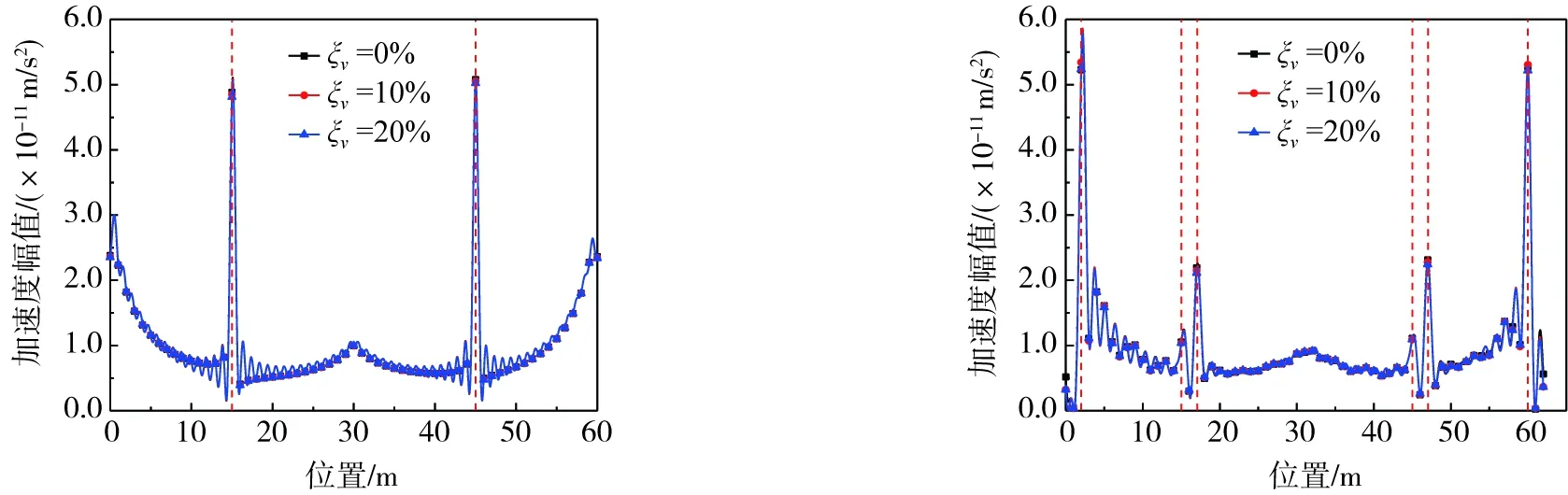
图18 IAS识别图(单轴车) 图19 IAS识别图(双轴车)

4 结论

1)车速对连续梁桥的损伤识别有较大影响,车速越高越不利于识别,车速小于等于6 m/s时,可以较为准确地识别出损伤程度为20%的裂缝损伤。滤波范围要适当,不可靠近车辆频率或者桥梁的第一阶频率。在车速较小时,车辆匀加速或者匀减速通过损伤处时,可以精确地识别出损伤位置。

2)桥梁损伤程度越大,IAS识别结果图中的峰值点越高,越易识别。IAS可以进行多裂缝损伤识别,并且也可以识别出位置比较接近的损伤,但是对于中支点处的损伤无法识别。车辆阻尼比对损伤识别的结果无影响。

3)在考虑路面粗糙度的情况下,提高量测车车重,以此增大对桥梁的激励可以很好地识别出A级粗糙度的桥梁损伤位置。

4)量测车采用单轴车或者双轴车都可以比较准确地识别出裂缝损伤的位置。车辆进出桥的时候,由于边界效应引起的强烈振荡会削弱结果的分辨率,从而导致桥梁两端IAS识别图中的幅值较大,对损伤识别造成了干扰,如果桥头处有损伤,识别较困难,这是此方法的局限性。