基于随机森林算法的城市空气质量评价研究*

尤 游

(安徽机电职业技术学院公共基础教学部 安徽芜湖 241000)

随着我国城市经济的高速发展和人民生活水平的提高，空气质量问题越来越受到全社会的广泛关注。近些年来，城市雾霾天气频繁出现，所引发的空气污染已经严重危害人们的工作生活，长期发展下去将会破坏生态平衡，同时也在一定程度上制约了城市的可持续发展[1]。为了加强空气污染防控治理，促进生态文明建设，2018年国务院发布了《打赢蓝天保卫战三年行动计划》[2]，进一步扩大了城市空气质量监测范围，在全国范围内将城市空气质量排名由原来的74个城市扩充到168个城市。因此针对全国168个重点环保城市进行空气质量评价，探索构建科学便捷高效的空气质量评价模型具有一定的代表性和参考价值，能够为相关环保部门治理大气污染提供理论决策依据[3]。

城市空气质量的好坏不仅与污染物(PM2.5、PM10、CO、NO2、SO2、O3)浓度有关，还包含气象因素如气温、降水量、风速、湿度、日照时数等以及其他一些不可控因素。针对城市空气质量评价，常用的模型如回归模型、模糊综合评价模型、聚类模型、ARIMA模型、BP神经网络等等。但随着科技的发展，监测技术和监测水平不断提升，空气质量数据逐渐呈现样本量大幅增长、特征属性复杂多样的特征，从而导致传统评价模型的弊端日益突显，已经不能满足大数据时代的评价需求[3]。近些年来，由于人工智能的兴起，机器学习越来越受到国内外学者的青睐。机器学习包含多个分支，如随机森林、决策树、支持向量机、朴素贝叶斯、逻辑回归、聚类、规则学习等[4-5]。目前机器学习已经广泛应用于金融、工业技术、生物医学、化工、新能源、网络安全等众多领域，机器学习算法的普及和推广给城市空气质量评价提供了新思路和新方向。

这里，随机森林(random forests，RF)是由美国Leo Breiman教授于2001年提出的一种机器学习算法。该算法包含多个决策树模型，且这些决策树通过选择最优特征属性进行节点分支。随机森林的优点在于能够处理海量监测数据，并且由于其训练样本选择和特征属性抽取的双重随机性，所以评价过程中无需考虑变量间的多重共线性，且避免了过拟合现象的发生，能够增强模型的泛化能力。

另外，由于bagging基本思想和决策树的组合优势，随机森林避免了局部最优解，其模型精度远高于单个决策树模型。所以基于城市空气质量监测数据的大样本特征和特征属性的复杂程度，利用随机森林算法来研究空气污染问题具有一定的可行性和前瞻性。

1 随机森林相关理论

1.1 随机森林分类

随机森林算法可以用于分类和回归，其中随机森林分类是基于原始样本集通过Bootstrap抽样法抽取样本子集构建多棵决策树，最终通过众数投票的方式来决定最优分类决策结果。其构建过程如图1所示，具体步骤如下[6-7]：

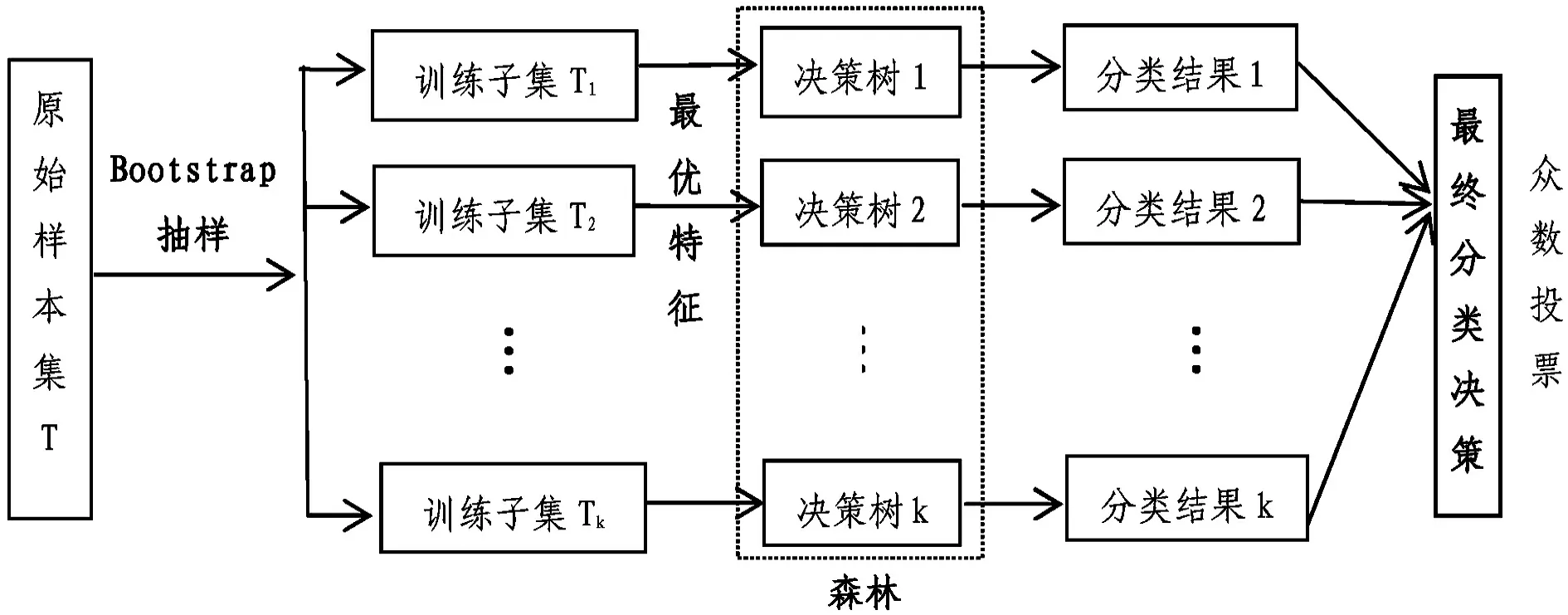
图1 随机森林分类模型构建流程

(1)利用Bootstrap抽样法即重抽样的方式，从原始训练样本集T中随机抽取t个相互独立的样本，这些样本构成新的训练子集，按照这样有放回的抽样k次，即获得k个相互独立的样本训练子集。

(2)针对随机抽取的训练样本子集开始构建k棵决策树，这里样本的所有N个特征属性并不全部参与节点分裂，而是随机选择其中n(n≤N)个属性作为分裂特征集，然后从特征子集里选取最优特征进行节点分裂，且由于抽样的随机性所以每棵决策树在节点优化前不需要剪枝处理而是让其最大程度的自由完整生长，这样产生的决策树集合就形成“森林”。

(3)生成的决策树模型包含了训练样本子集的分类准则和分类结果，可以依据该分类模型按照众数投票的方式来判别测试样本的类别。这里模型的分类决策结果为：

(1)

式(1)中，φp(x)表示单棵决策树的输出结果，φ表示分类类型，k表示决策树的个数，I表示线性函数。

1.2 影响因素重要性评价

随机森林算法可以利用袋外数据对各解释变量的重要性程度进行评价排序，其原理主要基于变量随机置换后均方误差减小量来衡量变量间的重要性[8-9]。具体步骤如下[8-10]：

(1)类似于随机森林分类，利用Bootstrap抽样法从原始训练样本集T中抽取k个训练样本子集来构建决策树模型。由于随机重采样的特性，所以会导致部分样本一直未抽中，当抽取的次数k趋向于无穷大时，即

(2)

意味着大约36.8%的样本从未被抽中，这部分样本通常称为袋外数据(Out Of Bag，OOB)[5，11]。袋外数据可以作为测试样本集来验证模型的精度。将袋外数据代入随机森林模型进行计算，可以得到对应的均方误差向量{MSEq}，其中q=1，2，…，b。

(2)由于随机森林特征属性抽取的随机性，所以每个变量Xp在OOB中可以被随机置换(随机改变特征值)，形成新的OOB测试样本集，按照步骤1的方法重新代入随机森林模型进行验证，可以获得特征改变后的OOB均方误差矩阵{MSEpq}，如下式(3)所示，其中p=1，2，…，m，q=1，2，…，b。

(3)

(3)用置换前的均方误差向量{MSEq}与置换后均方误差矩阵{MSEpq}的第p行向量对应相减，平均后再除以标准误差就可以获得每个变量的特征重要性量化指数FI：

(4)

2 变量选取和数据来源

该研究以全国168个重点环保城市为研究对象，选取X1，X2，…，X11等11个指标，包含6种空气污染物浓度和5种气象因素，分别为二氧化硫(SO2)年平均浓度(ug/m3)、二氧化氮(NO2)年平均浓度(ug/m3)、可吸入颗粒物(PM10)年平均浓度(ug/m3)、一氧化碳(CO)日均值第95百分位浓度(mg/m3)、臭氧(O3)日最大8小时第90百分位浓度(ug/m3)、细颗粒物(PM2.5)年平均浓度(ug/m3)、平均气温(℃)、年降水量(mm)、平均风速(m/s)、年平均相对湿度(%)、日照时数(h)，同时城市空气质量等级分类依据空气质量优良天数比例(%)来划分，具体如表1所示。

表1 空气质量影响因素列表

文中数据来源于2021年中国统计年鉴、各省市统计年鉴和相关气象网站，通过搜集整理获得168个城市的2020年空气质量影响指标数据和优良天数比例。依据数据查询结果并结合《2020年中国生态环境状况公报》可以了解到2020年全国168个重点环保城市平均优良天数比例为80.7%，某些重点区域如京津冀及周边地区平均优良天数比例为63.5%，长三角地区平均优良天数比例为85.2%，汾渭平原平均优良天数比例为70.6%[12]。

根据2020年生态环境部公布的全国168个重点环保城市空气质量排名情况，海口、拉萨、舟山、厦门、黄山、深圳、丽水、福州、惠州和贵阳等10个城市空气质量最好(排名前10)，而后10名城市依次是安阳、石家庄、太原、唐山、邯郸、临汾、淄博、邢台、鹤壁和焦作。

3 模型构建及仿真结果分析

3.1 随机森林分类结果分析

基于全国168个重点环保城市统计出的样本数据，根据空气质量优良天数比例分为三类，当优良天数比例大于等于90%时属于第一类，75%-90%之间属于第二类，小于等于75%时认为是第三类。依据以上比例，三类城市所属类别个数依次为43、69和56。这里按照7：3的比例将样本数据分为训练集和测试集。

下面利用MATLAB软件的fitctree()函数对训练集118个样本城市数据进行分类，采用的是CART决策树算法[13]。该算法在每个节点分支上只考虑二元划分，所以构建的决策树属于二元决策树[1]。决策树的特征属性为6种空气污染物(S02、N02、PM10、CO、O3、PM2.5)浓度，训练得到的决策树模型如图2所示。

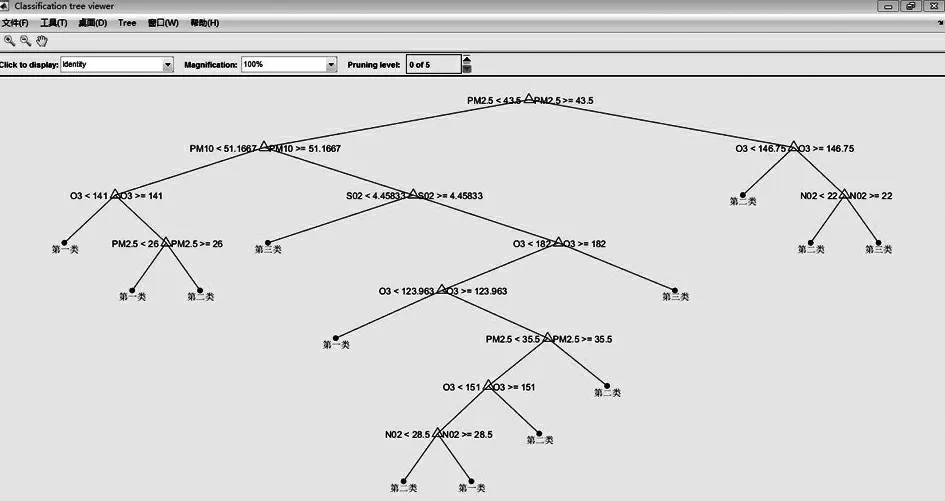
图2 空气质量类别决策树分类

在此基础上对测试集的50个样本数据进行分类判别，得到的分类模型混淆矩阵如表2所示，统计出测试样本集得到正确分类的为45个，分类总体正确率为90%。

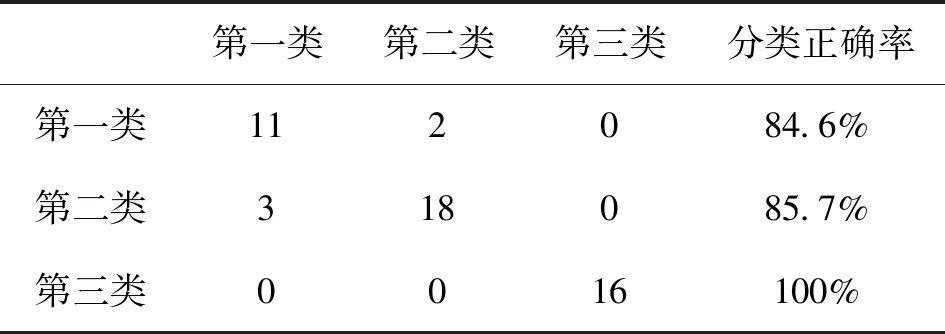
表2 随机森林分类模型混淆矩阵表

3.2 基于随机森林空气质量影响因素重要性评价

基于168个城市样本数据进行空气质量影响因素重要性评价，将SO2、NO2、PM10、CO、O3、PM2.5、平均气温、年降水量、平均风速、年平均相对湿度、年日照时数等11组自变量数据作为模型的输入变量，将因变量数据空气质量优良天数比例作为模型的输出变量。为了科学评价11个影响因素的重要性程度，将采用MATLAB软件进行仿真训练。

首先确定最优叶子节点数和决策树的个数[14]：先设置初始叶子节点数分别为5，10，20，50，100，200，500，通过均方误差的大小来判断最优节点数。训练结果如图3所示，均方误差最低的线是红色的，所以认为当叶子节点数为5时模型精度最佳。在此基础上继续观察决策树个数对均方误差的影响，可以看出当决策树个数近似到100时其均方误差不再下降，此时几乎趋于稳定。所以综合分析认为当叶子节点数为5、决策树个数为100时随机森林模型的性能最优。

图3 均方误差曲线图

接下来进行影响因素重要性评价，这里重要性程度通过feature importances来描述，且将各个因素对空气质量的影响程度归一到(0，1)区间来量化。训练得到基于随机森林的空气质量影响因素重要性程度排序情况如图4所示。

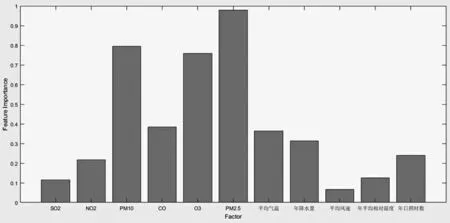
图4 空气质量影响因素重要性排序柱状图

由图4可知11个影响因素重要性程度从高到低排序依次为PM2.5、PM10、O3、CO、平均气温、年降水量、年日照时数、NO2、年平均相对湿度、SO2和平均风速，其中PM2.5、PM10和O3的影响程度均超过0.7，是影响空气质量最主要的污染源。

4 结语

文章通过收集全国168个重点环保城市空气质量影响指标数据，利用机器学习中的随机森林算法对空气质量等级进行分类决策，得到测试样本集的分类准确率为90%[15]。在此基础上可以根据构建的决策树模型对其他待判城市进行评价，快速获得其空气质量类别。进一步对城市空气质量的11个影响因素进行重要性评价排序，科学锁定主要污染源为PM2.5、PM10和O3，帮助政府和相关环保部门有针对性的采取空气污染防控治理措施，以此改善生态环境。该模型可以实时有效评价城市空气质量类别，促进空气污染智能监测、分析研判和综合治理水平的提升，推进区域间环境治理的联防联控。