简单随机游动通道概率的估计*

梁 静

(淮南师范学院金融与数学学院 安徽淮南 232001)

数学家O.Schramm首先将复分析中的Loewner理论与随机分析相结合，创立了SLE理论[1].他首次给出了尺度极限的严格定义，并且引入SLE来描述尺度极限.他进一步证明了，环删除随机游动 (LERW)的尺度极限存在并且满足共形不变性质，收敛于SLE2[2].后续运用SLE可以描述以下模型的极限情形，调和测度收敛于SLE4[3]，三角形网格中的临界渗流收敛于SLE6[4]，一致生成树收敛于SLE8[5-7].文献[7]中给出了误差的范围，文章在其基础上通过表示出作为领域内径的幂更精确的误差，进而给出了简单随机游动的通道概率的优化估计.

1 预备知识

在这一节中给出文章涉及的一些定义、记号以及一些基本事实，更详细的请参见文献[8-10].

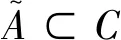
分别为离散泊松核与泊松核.

假定A是Ζ2的子集，令τA=min{j≥0：Sj∈∂A}.对于x，y∈∂A，定义离散游弋泊松壳h∂A(x，y)=Px{SτA=y，S1∈A}.有

(1)

(2)

(3)

其中，GA为A上自由随机游动的格林函数.

引理1 (Komlo's-Major-Tusna'dy定理)存在常数c<∞，在概率空间(Ω，F，P)上分别定义一个二维布朗运动B和二维简单随机游动S且B0=S0.使得对所有的λ>0，对于每一个n∈N，

(4)

引理2 (强逼近)存在常数c<∞，在概率空间(Ω，F，P)上分别定义一个二维布朗运动B和二维简单随机游动S且B0=S0，使得：

(5)

(7)

2 简单随机游动通道概率的估计

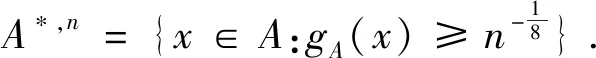
(8)

δ′(n)=minP*{SτA=y}，∀M<∞，A⊂Ζ2，σM=σM，A=min{j≥0：dSj≤M}.

(9)

引理4[7]对于每个ε>0，存在δ>0使得如果A是Z2的有限连通集，V⊂∂A，x∈A，且H(x)≥ε，那么h(x)≥δ.

命题1 存在常数c1，c2，c3，ε，使得如果A∈Α，x∈A，且dA(x)≤c1

σ=min{j≥0：Sj∉A，dA(Sj)≥(1+c1)dA(x)，或者|θA(Sj)-θA(x)|≥c2dA(x)}

(10)

则有Px{Sσ∉A}≥ε，Px{Sσ∈A，dA(Sσ)≥(1+c1)dA(x)}≥ε以及

Px{|θA(Sσ)-θA(x)|≤c3dA(x)|Sσ∈A}=1

(11)

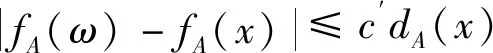
z∈Sx(12)

|fA(z)-fA(x)|≤c′|fA(z′)-fA(x)|

z，z′∈Sy(13)

Px{Sσ∉A}≥ε，

Px{Sσ∈A，dA(Sσ)≥(1+c1)dA(x)}≥ε

(14)

同时，如果y，ω∈A，|y-ω|=1，dA(y)≤dA(x)，且|θA(y)-θA(x)|≤c2dA(x)，那么

|fA(ω)-fA(x)|≤|fA(ω)-fA(y)|+|fA(y)-fA(x)|≤c3dA(x)

(15)

即对于某个特定的c2，有|θA(ω)-θA(x)|≤c2dA(x)，由此命题1得证.

由命题1和推论1，即可得

引理5 对于A∈Αn，令η=min{j≥0：Sj∈A*，n∪AC}.存在常数c，α使得如果A∈Αn，x∈AA*，n，且r>0，有：

(16)

(17)

Px{ξ<η}≤c0n-5Px{Sη∈A*，n}.

(18)

y∈A*，n(19)

y∈AA*，n(20)

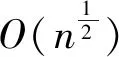
(21)

(22)

对于GA(y)有类似结果.因而，对于任意x∈AA*，n，有

GA(x)=Px{Sη∈A*，n}Ex[GA(Sη)|Sη∈A*，n]

(23)

(24)

(26)

(27)

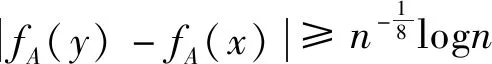
(28)

(29)

因而，可知：

GA(x，y)=Px{Sη∈A*，n}

(30)

式(30)结合式(22)可推出式(19)，如果y∈∂iA*，n，那么有：

(31)

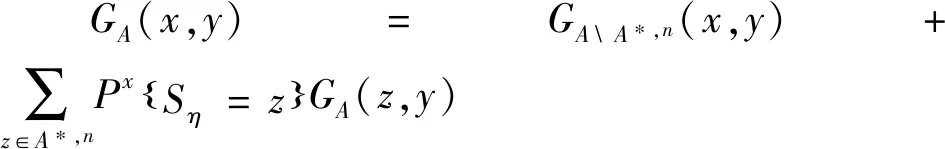
(32)

(33)

证明：由a式(1)、式(2)、式(3)及引理6即可得定理1.