离散可积系统在求解非线性晶格方程中的应用研究*

朱永芳

(安徽三联学院基础部 安徽合肥 230601)

人类对自然界的认识呈螺旋式曲折上升，科学家逐渐意识到非线性是现实世界的普遍特性，其中孤立子理论和可积系统的研究不断完善着非线性的科学体系.孤立子波是非线性波动方程的一类脉冲状的行波解[1].线性的波动方程具有行波解，时间坐标和空间坐标作为方程的组合变量.波形随着时间的发展而不断向前推进，但是色散效应的存在使得波的不同部分频率不同，传播速度也不相同.非线性系统的波在前进中不仅存在色散效应的干扰，还会出现非线性项，两种作用同时存在又可互相抵消，因此出现孤立波解[2-3].孤立波具有质量特性，遵循能量守恒定律和弹性守恒定律，因此可将其视为粒子，又名孤立子.大量的方程均可用孤立子理论证明其可积性.其中非线性微分差分方程可作为求解金融问题、超导问题、生物科学问题和光线通行问题等的数学模型，具有广泛的应用前景[4].

左茂武等人针对两艾里-高斯光束在非局域性非线性缺陷晶格中的相互作用，通过讨论其光束入射角、两光束相位差等方式进行了数值研究，成功发现可形成两个不同传输方向的孤子对[5].Camassa R对完全可积浅水方程的初值问题进行了探究，发现当产生的有限维投影到其一类分布解上时，能够采用粒子法来实现对波动方程的数值求解[6].鉴于此，该研究构造了离散的特征值问题，将等谱问题的双非线性化应用至离散可积系的求解问题中.

1 一族微分差分方程族的可积辛映射

1.1 离散可积系统的Hamilton结构

有限维Hamilton系统可通过Liouville-Arnold定理证明其可积性，但无限维的Hamilton系统无法使用有限维的证明思路实现求解，只能从局部研究其性质.该研究首先寻找其Lax可积、构建Hamilton结构，其次通过前述分析基础寻找其可积辛映射.

(1)

(2)

(3)

公式(3)中的J是哈密顿算子，L为递推算子.研究使用迹恒等式构建Liouville可积的Hamilton结构，得出离散等谱问题的屠格式.

令V=ΓU-1=

(4)

将公式(4)带入迹恒等式，可得：

(5)

令公式(5)中的n=1，可得ε=0.故公式(3)可写为Hamilton形式：

(6)

公式(6)中的J为Hamilton算子，可验证(JL*)=-JL.

利用J定义Poisson括号{f，g}J=

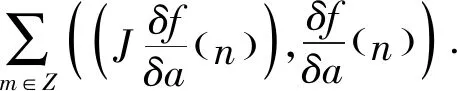
(7)

(8)

1.2 Bargmann约束下的双非线性化

非线性微分差分方程系统具有空间离散化的特性，求解过程相较其他类型的方程更为复杂，目前学术界常使用双非线性化理论构建其可积辛映射，并通过合适的对称约束求解方程族的解[7-8].Lax方程的函数表达式为：

(9)

记Φi=(φi1，φi2，..，φiN)T，Ψi=(Ψi1，Ψi2，..，ΨiN)T，i=1，2，可得到显示表达式：

(10)

(11)

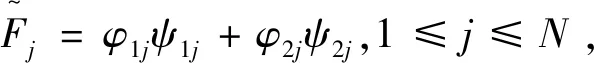
(12)

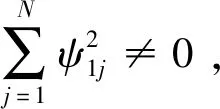
(13)

(14)

2 Toda晶格方程的Hamilton结构及其非线性化

Toda晶格方程是一种特殊非线性势函数的非线性晶格方程，目前应用较为广泛的微分差分模型，它可以描述声波在固体内的传播过程，局域集波在固体内传输，会与固体材料的原子发生碰撞，该原子在碰撞发生的瞬间获得位移，但是碰撞结束之后该原子重新恢复至原有状态[9-10].Toda晶格方程可写为：

(15)

公式(15)中的rn表示第n个离子离开平衡位置的距离，f(rn)表示离子受到的作用力，且有f(r)=-α(1-e-βr).容易验证，低阶的Bagmann约束在处理Toda晶格方程问题上是无效的，因此该研究选用高阶Bagmann约束，其公式为：

(16)

相应谱参数λ对于位势u的变分导数中i=1，2，j=1，2，...，N.特征函数在无穷远处趋近于零.容易得到：

(17)

由于Φi=(φi1，φi2，...，φiN)T、Ψi=(ψi1，ψi2，...，ψiN)T，i=1，2，Λ=diag(λ1，λ2，...，λN)，若选取aj=1，j=1，2，...，N，则可得：

(18)

由此可得到一个离散的Bagmann系统：

(19)

公式(19)中j的取值范围为[1，N].

设fi=fi(Φ1，Φ2，Ψ1，Ψ2)，gi=gi(Φ1，Φ2，Ψ1，Ψ2)，且i的取值范围为[1，2N].则有：

(20)

公式(20)中的j的取值范围为[1，N].

在任意R4N空间内的任意函数f、g，研究引入泊松括号的定义，具体公式如下：

(21)

(22)

由上述结果，可以得到以下定理：

定理1：辛映射公式H(Φ1，Φ2，Ψ1，Ψ2)=(EΦ1，EΦ2，EΨ1，EΨ2)是可积的，并且有限维Hamilton系统公式在Liouville意义上是可积的.

定理2：若(Φ1(n，tm)，Φ2(n，tm)，Ψ1(n，

tm)，Ψ2(n，tm)是离散系统公式和完全可积的有限维Hamilton系统公式的一个解，则Toda晶格方程的一个解为：

(23)

上述过程提供了一种求解Toda晶格的方式，且公式(23)可看作是完全可积的有限维Hamilton系统公式(22)的一个Bäcklund变换.

3 结语

非线性演化方程的结构较为复杂，无法求得其平凡解，目前关于非线性微分差分方程的研究主要集中在构造方程簇、晶格系统求解、具特殊相干结构的微分差分晶格和系统的数值研究上.文章首先提出了一个新的离散特征问题，根据离散零曲率方程，得到一族微分差分方程，对其Lax对和伴随Lax对进行双非线性化，将原有方程组约化.遵循该思路，研究从新的矩阵谱问题出发，得出新的离散可积系统和典型Toda晶格方程，使用高阶Bagmann约束对其Lax对和伴随Lax对进行双非线性化，通过求解辛映射和有限维Hamilton系统，得到原可积系统的一个精确解.在使用高阶Bagmann约束时，算子E-1的产生给运算造成了较大困难，无法使用该方法对所有微分差分方程进行求解，还需要继续研究将对称约束与其他技术结果研究微分差分方程的可积耦合.